堆石矮堰清水冲刷历时发展特性
2022-09-14杨克君刘兴年聂锐华
张 文,王 路,杨克君,刘兴年,聂锐华
(四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065)
近年来,随着社会经济的发展,以航运、灌溉、发电等为目的在河流中修建了大量水工建筑物(如高坝、矮堰、丁坝等)[1- 3],严重影响了河流水沙运动、河床演变和生态环境,使河流健康面临巨大威胁。传统观念认为,高坝工程的修建会破坏河流生态,是导致河流健康恶化的主要因素之一。但相关研究表明[4],低水头河道整治建筑物对河流健康的影响同样不可忽视。Belletti等[5]调查显示,截至2020年,欧洲全域已修建了超120万座涉河建筑物,其中,高坝(高度大于15 m)仅占约1%,低水头河道整治建筑物(高度低于2 m,如矮堰、底槛等)则占比近62%,大大降低了河流连通性。在中国,河流健康同样面临大量低水头水工建筑物的威胁。陈求稳等[1]总结了近年来国内外水电工程生态环境效应的研究进展,指出广泛分布在国内支流的小型拦河堰坝存在量大面广、建设技术落后等问题,严重影响了河流生态。Kibler等[6]基于对怒江流域的野外调查,发现大量修建的小型拦河堰严重破坏了流域水生栖息地和水文情势的稳定,对河流生态的负面效应远超高坝工程。因此,为了提升或恢复河流健康,越来越多的河流修复工程选择拆除已建的河道整治建筑物,或者采用生态友好的河道整治建筑物[7]。
堆石矮堰(rock weir)是常用的“生态友好型”河道整治建筑物,由天然石材或碎石构成[8]。与传统矮堰(衬砌或钢混结构)相比,堆石矮堰有以下优点:堆石能提升河床结构的多样性,为水生生物提供栖息地和产卵场所[9];透水性强,既能增加河流连通性[10],也能促进水流交换和调节水温[11];堰后跌水能提高水体溶解氧浓度,增加鱼卵氧含量[12]。由于具有良好的生态效益和取材方便、施工简单等优点,堆石矮堰被广泛应用于河流修复与治理工程[13]。然而,由于设计不当,堆石矮堰的水毁率非常高。Mooney等[14]调查了美国127座堆石矮堰,发现有70%的堆石矮堰发生了失稳或破坏,其中大部分是由过堰水流产生的冲刷所致。因此,为了提升结构设计的可靠性,有必要对堆石矮堰的局部冲刷开展系统深入研究。
近年来,许多学者围绕堆石矮堰的冲刷机理开展了大量研究。Scurlock等[15]基于水槽试验,研究了顺直河道中A型、U型和V型堆石矮堰的清水冲刷机理,分析了结构几何形态、水流条件和床沙组成对堆石矮堰清水冲刷尺度的影响规律;Pagliara等[16- 17]基于水槽试验,探明了顺直河道中河床坡度和矮堰淹没度对I型、U型和W型堆石矮堰清水冲刷尺度的影响机制;Pagliara等[18- 19]基于水槽试验,揭示了顺直和弯曲河道中堆石矮堰的冲刷机理,发展了Pagliara等[16]提出的冲刷计算模型;Kupferschmidt等[20]基于室内水槽试验,研究了定床条件下I型和V型堆石矮堰附近的流场特性,发现V型(开口向下游)堆石矮堰能够减少岸边水流流速,从而减少岸坡冲刷;Khosronejad等[21]基于三维水沙耦合动力模型(CURVIB)[22],成功模拟了清水冲刷条件下堆石矮堰的平衡冲刷形态。然而,上述研究大多关注堆石矮堰的平衡冲刷形态,对堆石矮堰清水冲刷尺度的历时发展特性认识不清。在清水冲刷条件下,堆石矮堰冲刷达到平衡通常需要数天或更长时间[15],而天然河道中的洪峰流量通常仅持续数小时或数十小时[23]。因此,已有基于洪峰流量的平衡冲刷计算方法可能会严重高估堆石矮堰的清水冲刷尺度而增加堆石矮堰的建造成本。为此,有必要系统研究堆石矮堰清水冲刷的历时发展特性,提高堆石矮堰清水冲刷尺度的计算精度。
本文开展水槽试验,分析水流强度、矮堰透水性、矮堰淹没度对堆石矮堰清水冲刷尺度发展过程的影响,以揭示堆石矮堰清水冲刷历时发展特性;基于理论分析与试验数据,提出堆石矮堰历时清水冲刷深度、长度、体积的计算方法。本文研究成果以期加深对堆石矮堰清水冲刷机理的认识,提高堆石矮堰清水冲刷尺度的预测精度,为堆石矮堰冲刷设计、防护和后期维护提供支撑。
1 试验方案
试验在四川大学水力学与山区河流开发保护国家重点实验室开展。试验采用顺直玻璃边壁水槽(图1),长12 m,宽0.5 m,深0.5 m。水槽进口处安装PVC管组成的蜂窝状花墙,用于消能和平顺水流;出口处安装闸门,用于控制尾水深度。水槽与实验室循环供水系统连接,水流流量采用矩形薄壁堰进行测量。水槽两侧各布置1个摄像头,结合玻璃边壁上粘贴的透明网格纸,用于记录、测量水位和床面形态(精度±2 mm)。
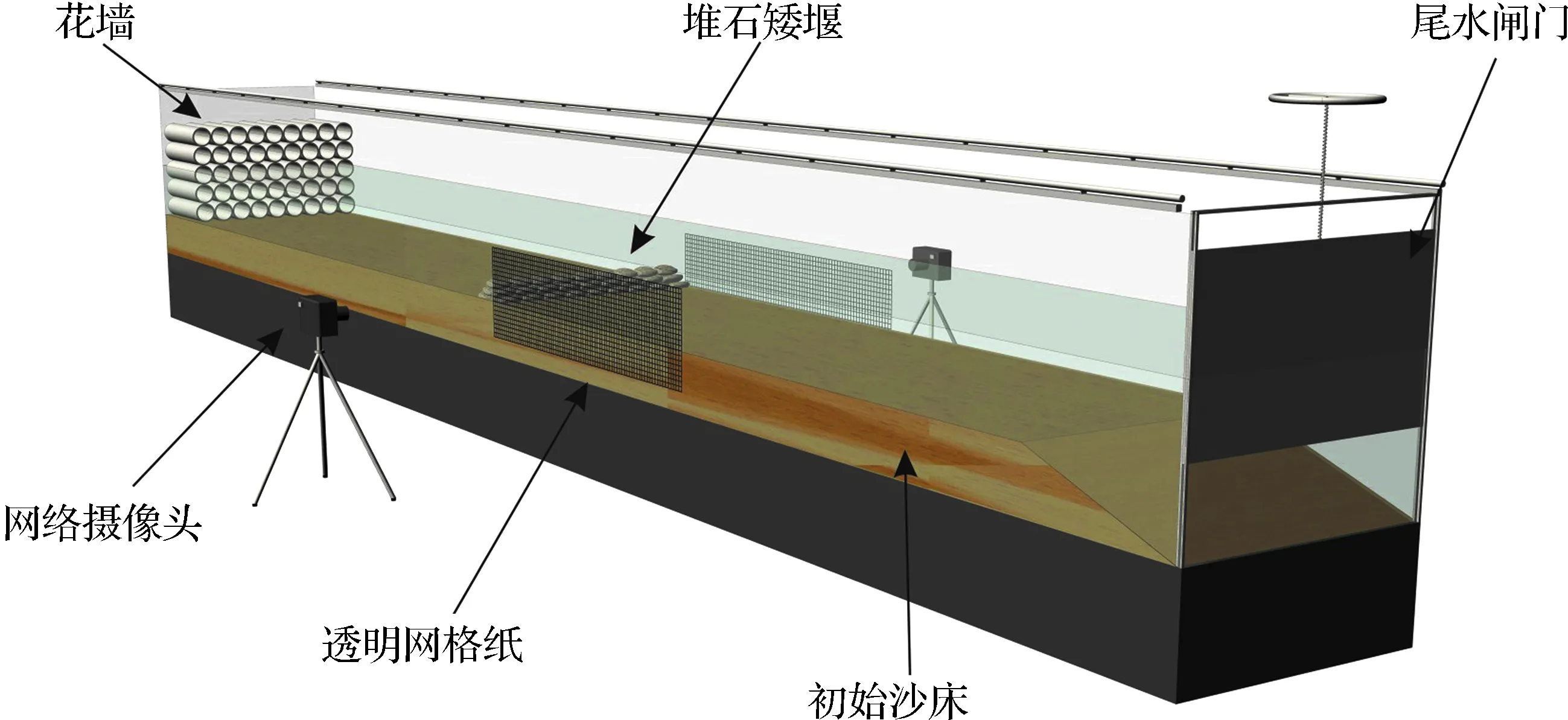
图1 试验水槽和测量设备示意Fig.1 Experimental flume and measurement devices
试验主要参数和坐标系如图2所示(ds为冲刷深度,mm;ls为冲刷长度,mm;h0为矮堰上游水深,mm;ht为尾水深,mm;U0为矮堰上游平均流速,m/s;Hd为矮堰上下游水位差,mm;z为堰高,mm;φ为堰坡角度, °)。坐标原点位于堰下游坡面和初始床面线的交点。试验采用均匀粗砂在水槽中铺设约200 mm厚的河床(中值粒径d50= 1.27 mm;水下相对密度Δ=1.65;非均匀系数σg= (d84/d16)0.5=1.26,d84和d16分别为床沙累计频率分布百分数达到84%和16%时对应的粒径),避免冲刷深度触及水槽底板[2]。试验采用的堆石矮堰尺寸和形状参考设计规范[8]。堆石矮堰由均匀松散石块组成(粒径D=12 mm、D=24 mm、D=33 mm,堆石的短轴大于长轴的1/3),置于水槽进水口下游约6 m处。堆石矮堰的上、下游堰坡角度均等于堆石的水下休止角(约40°)。为了避免堰体沉降和局部冲刷对堰体稳定的影响,矮堰底部用同样石材堆砌了与堰体相似、3.0~3.5倍堰高的基座[8],远大于本研究试验中的最大冲刷深度1.3z。
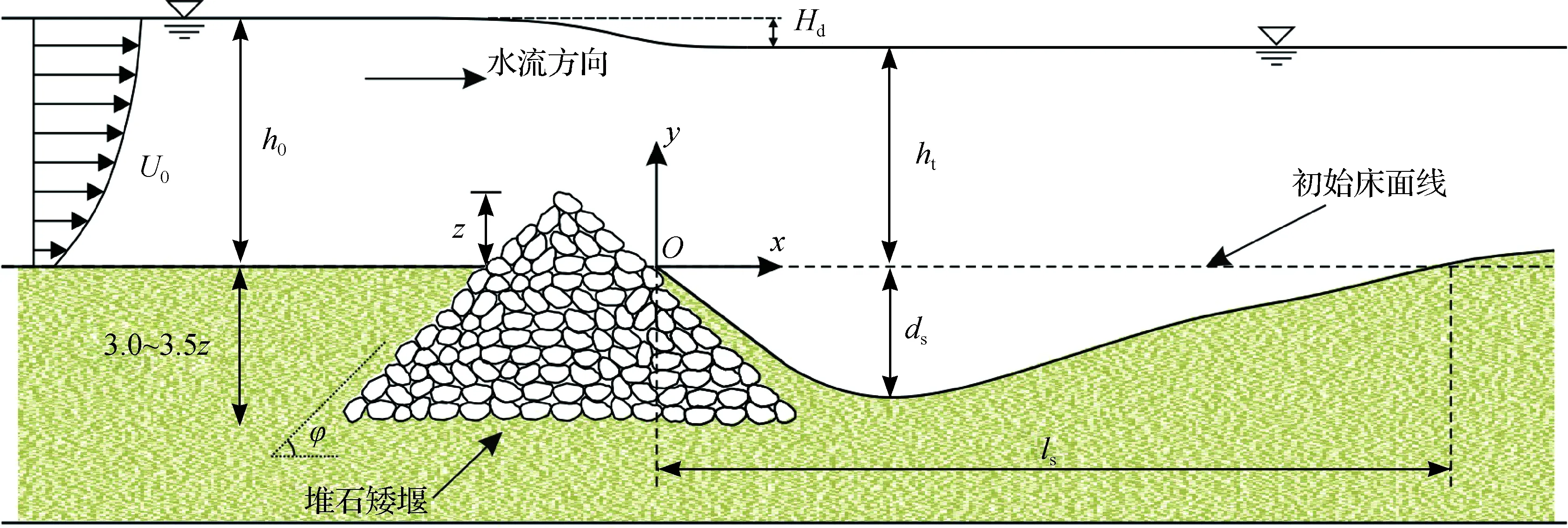
图2 试验主要参数与定义Fig. 2 Definition of the main test variables
试验条件如表1所示,其中,Q为水槽流量;Uc为临界泥沙起动平均流速,可根据流速对数分布公式Uc/u*c=5.75log(5.53h0/d50)计算,临界摩阻流速u*c按照Melville[24]的方法计算;Fru为矮堰上游来流的弗劳德数;T为试验时长;S为初始床面坡度。试验共采用了3种堰高(z=30 mm、z=40 mm和z=50 mm)和5种水深(ht=60 mm、ht=80 mm、ht=100 mm、ht=120 mm和ht=150 mm),控制堆石矮堰的淹没度
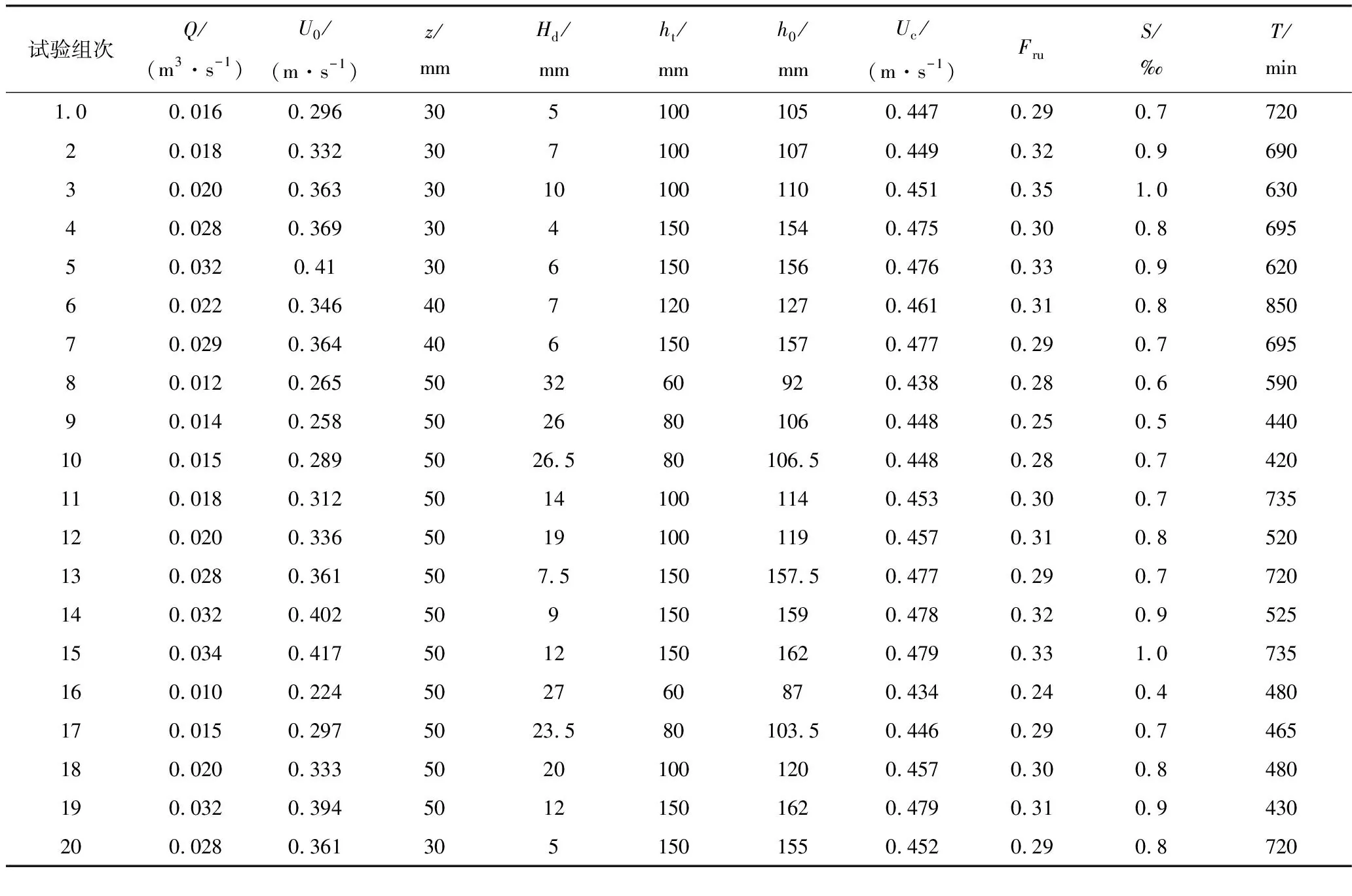
表1 试验条件
z/ht<1,与设计规范[8]中要求一致,即堆石矮堰时常处于部分淹没或完全淹没的状态。表中各组试验的弗劳德数均小于1,表明试验水流为缓流。所有试验均在清水冲刷条件下进行,即矮堰上游床面泥沙未起动(U0/Uc< 1)[25]。为了避免堆石矮堰结构失稳影响冲刷过程,本研究基于一系列预试验确定了堰体不被水流冲散的试验条件。为了使试验的初始水流为近似均匀流,试验开始之前基于预试验确定了各组试验的初始床面坡度。

本文首先基于试验结果,采用量纲分析方法得到与堆石矮堰清水冲刷尺度历时发展过程相关的量纲一参数;然后通过单变量分析(控制其他参数不变)探究各量纲一参数与冲刷尺度历时发展过程的量化关系;最后基于试验数据和探明的量化关系,结合回归分析提出堆石矮堰历时冲刷深度、长度和体积计算方法。
2 试验结果分析
2.1 冲刷深度与冲刷长度
在恒定流条件下,冲积河流中堆石矮堰的冲刷尺度(ys,即ds和ls)主要受以下参数的影响:
ys=f(b,z,D,ν,ρ,g,ht,h0,U0,ρs,d50,σg,T,Te)
(1)
式中:b为堰宽,mm;ν为水体运动黏度,m2/s;ρ为水体密度,kg/m3;ρs为泥沙密度,kg/m3;g为重力加速度,9.81 m/s2;Te为冲刷平衡时间,min。
对于给定的ht,h0是U0与z的函数[26],可从式(1)中省略。对于充分发展的紊流,运动黏度对冲刷的影响可忽略不计[28]。由于本试验使用均匀沙,且堰宽保持不变,σg和b可从式(1)中省略。因此,假设水体密度、泥沙密度不变,式(1)可改写为
(2)

(3)
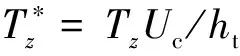
(4)
图3展示了各试验组次中量纲一冲刷深度(ds/dsz,dsz为特征冲刷深度)与冲刷长度(ls/lsz,lsz为特征冲刷长度)的历时发展过程。总体上,冲刷深度和冲刷长度的发展速度在试验初期相对较快,随着冲刷的发展,两者的发展速度逐渐变缓。图3展示的堆石矮堰清水冲刷结果与许多涉河建筑物(如桥墩、丁坝、传统矮堰等)的清水冲刷历时发展规律相似[27,31- 33]。因此,和这些涉河建筑物相同,堆石矮堰的清水冲刷尺度与时间的关系可以用指数函数来描述[27]:
(5)
式中:C1,C2和n均为待定系数。由于式(3)中指出堆石矮堰的清水冲刷尺度还与U0/Uc、z/ht和D/z相关,因此,基于式(3)和式(5),堆石矮堰清水冲刷尺度与时间的关系可描述为
(6)
式中:n1—n4为待定系数。下文将分析ys/ysz(即ds/dsz和ls/lsz)对U0/Uc、z/ht和D/z的敏感性,明确式(6) 右侧各参数对清水冲刷深度和冲刷长度历时发展特性的影响。
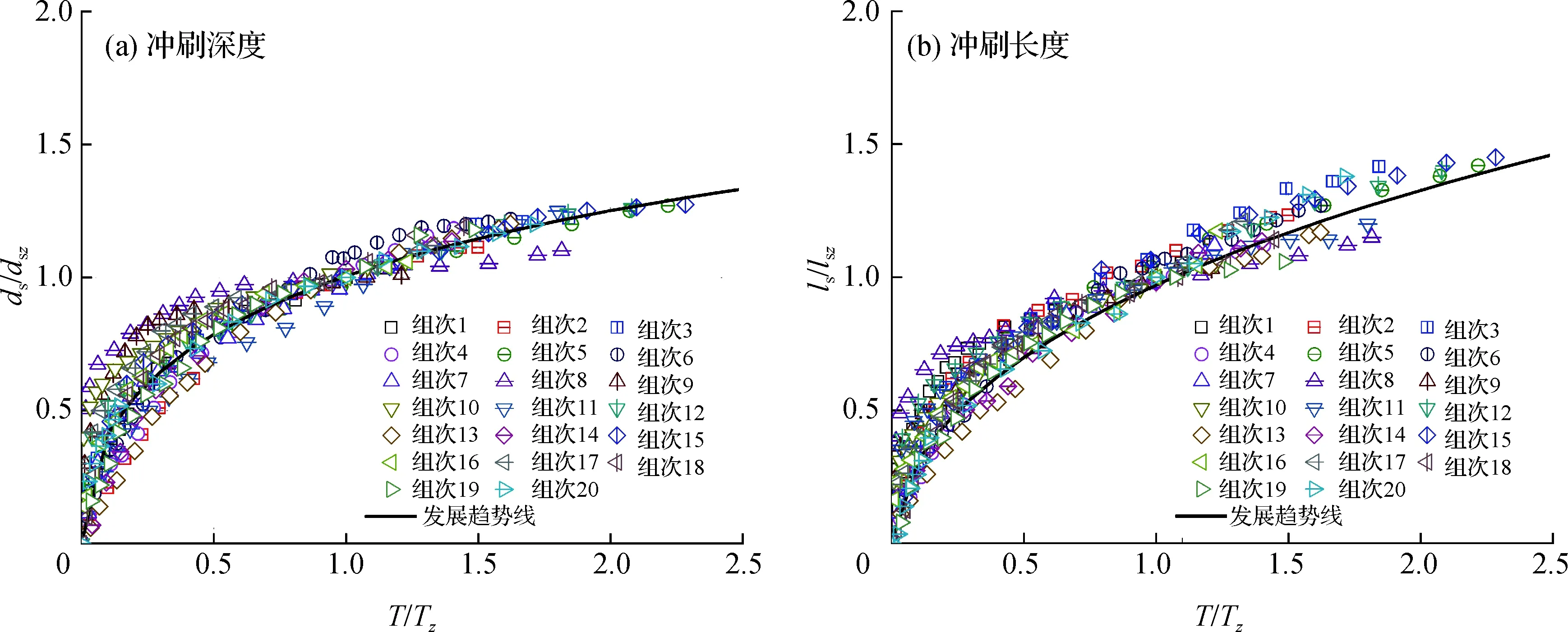
图3 冲刷深度和冲刷长度的历时发展过程Fig.3 Temporal evolution of scour depth and scour length
图4展示了U0/Uc对冲刷深度与长度历时发展过程的影响。从图4中可以看出,当z/ht和D/z不变时,在任一量纲一时刻T/Tz的冲刷深度和冲刷长度均随U0/Uc的增大而增大。这是因为在清水冲刷条件下,上游河道无泥沙运动,U0/Uc的增加仅增强越堰水流的强度,从而加速了冲刷深度和冲刷长度的发展。
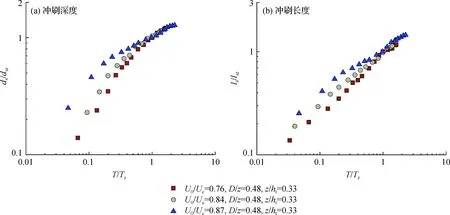
图4 水流强度对清水冲刷深度和冲刷长度历时发展过程的影响Fig.4 Effect of flow intensity U0/Uc on the temporal evolution of scour depth and scour length
图5展示了z/ht对冲刷深度与长度历时发展过程的影响。图5中可以看出,当U0/Uc和D/z不变时,在任一量纲一时刻T/Tz的冲刷深度和冲刷长度随着z/ht的增大而增加。这一试验结果与淹没度对越堰水流流速的影响相关。当z/ht较小时(高淹没度),堰体对越堰水流的束窄作用较小,对越堰流速的影响相对较小;随着z/ht增加,堰体对越堰水流的束窄作用增加,导致越堰流速增大,从而加快冲刷深度和冲刷长度的发展。

图5 矮堰淹没度对清水冲刷深度和冲刷长度历时发展过程的影响Fig.5 Effect of submergence z/ht on the temporal evolution of scour depth and scour length
图6(a)和图6(b)分别展示了量纲一堆石粒径对冲刷深度与冲刷长度发展过程的影响。可见,当z/ht和U0/Uc不变时,在任一量纲一时刻T/Tz的冲刷深度和冲刷长度随着D/z的增大而分别减小和增加。Guan等[26]指出矮堰下游的冲刷尺度受越堰水流流速与下游湍流强度的影响。Leu等[34]认为堰体透水性增大会降低越堰流速与下游湍流强度,但使高湍动区域向下游扩展。因此,D/z增大(矮堰透水性增大)降低了越堰流速和冲刷区域的湍流强度,从而减少了冲刷深度;由于D/z增大使高湍动区域向下游扩展,从而增加了冲刷长度。
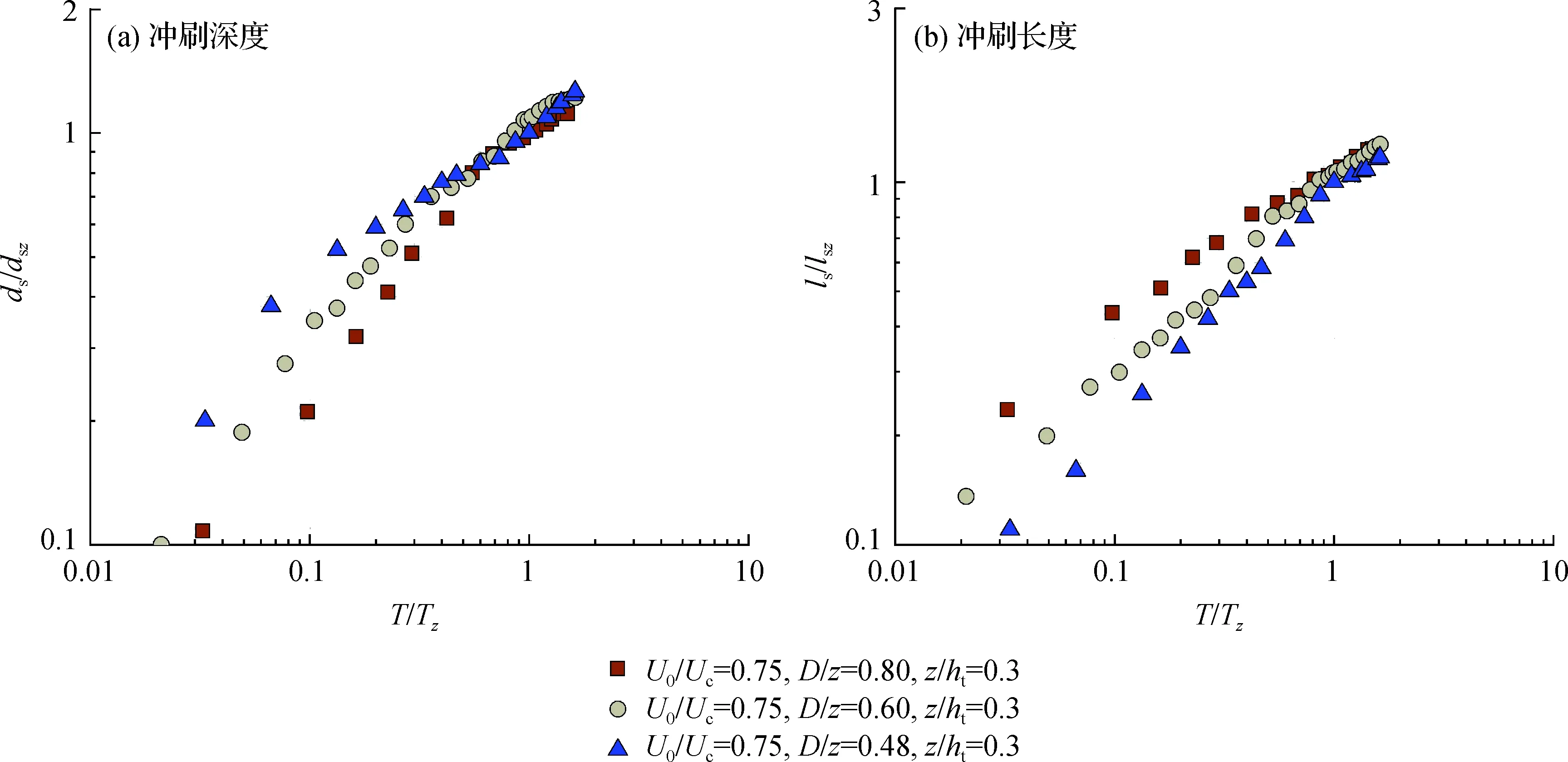
图6 量纲一堆石粒径对清水冲刷深度和冲刷长度历时发展过程的影响Fig.6 Effect of dimensionless rock size D/z on the temporal evolution of scour depth and scour length
基于图4—图6所示的量化关系,结合本文所有试验数据和式(6),可以得出堆石矮堰清水冲刷深度和冲刷长度历时变化的表达式:
(7)
(8)
式(7)和式(8)相关系数(R2)分别为0.93和0.95。式(7)中特征冲刷深度取z,式(8)中特征冲刷长度基于本文试验数据可取为21z。
2.2 特征时间比尺
应用式(7)和式(8)时需要已知特征时间,因此,本小节将基于式(4)分析参数U0/Uc、z/ht和D/z对特征时间比尺的影响。

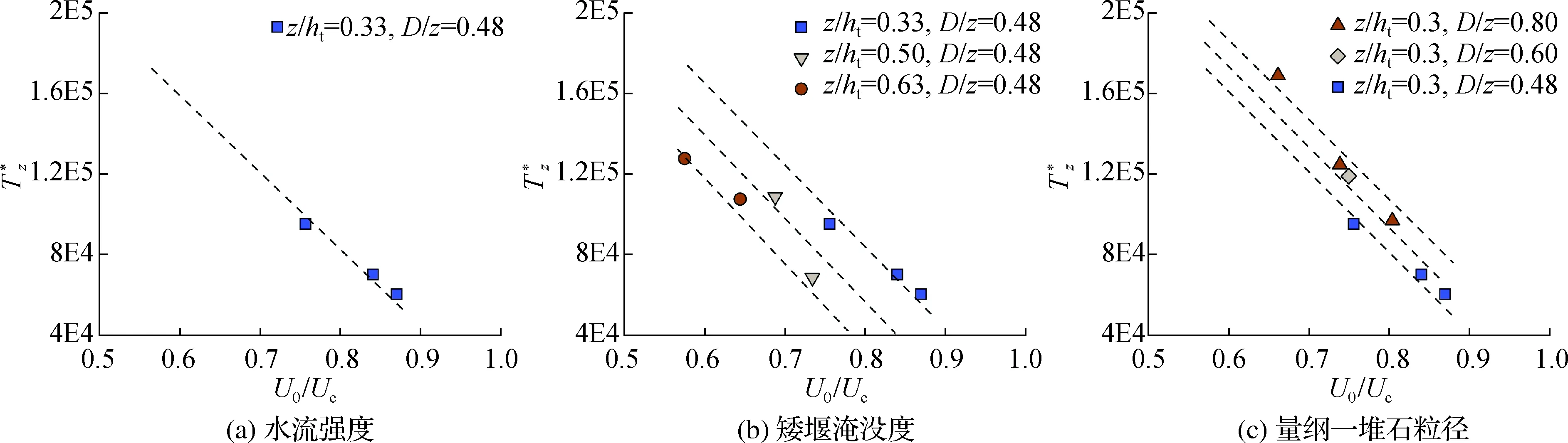
图7 试验变量对特征时间比尺的影响Fig.7 Effect of tested parameters on characteristic time scale
基于上述量化关系,结合本文试验数据和式(4),可得特征时间比尺的表达式(式9),该公式相关系数为0.86。
(9)
需注意,式(7)—式(9)使用的前提是平衡冲刷深度能够达到或大于堰高,该条件可根据堆石矮堰平衡冲刷深度计算方法[8]来判断。
2.3 冲刷坑形态和体积
除冲刷深度和冲刷长度外,矮堰的冲刷体积也是重要的设计参数,合理预测冲刷体积可为确定冲刷防护设施的保护范围提供依据[35]。由于本研究的冲刷坑形态近似二维,因此只需知道冲刷坑的纵剖面面积就能确定冲刷体积。
图8展示了试验组次5中的量纲一冲刷纵剖面的发展过程。图中Xs(t)和Ys(t)分别为t时刻冲刷坑纵剖面上某点处的横、纵坐标值;Xs,m(t)和Ys,m(t)分别为t时刻冲刷坑纵剖面上最大的横、纵坐标值的绝对值(分别等于该时刻冲刷长度和冲刷深度)。由图8可知,在冲刷发展初期,量纲一冲刷纵剖面形态不断变化,但超过某一时刻(t=330 min),量纲一冲刷纵剖面开始收敛(最大冲深点的量纲一横坐标每小时变化小于2%),几乎不再随时间变化。
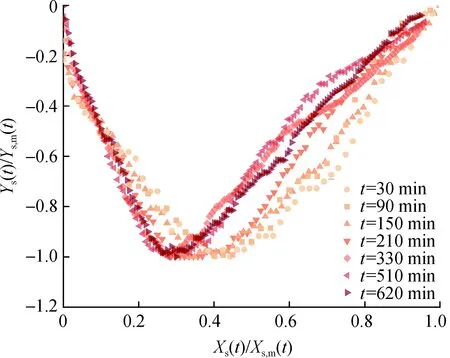
图8 试验组次5中量纲一冲刷纵剖面的发展过程Fig.8 Temporal evolution of the dimensionless scour hole profile in No.5 test run
本文借鉴并采用Lu等[31]描述传统矮堰冲刷坑纵剖面形态的函数形式,来表达堆石矮堰收敛后的冲刷坑纵剖面形态:
(10)
式中:a,b和c为待定系数。基于本文试验数据确定a、b、c的值后,式(10)可写为
(11)
式(11)的相关系数为0.85。图9对比了式(11)的计算值与实测值,平均绝对误差为20.7%(5.6%~48.7%),显示式(11)有相对较高的精度。

图9 计算与实测量纲一冲刷纵剖面对比Fig.9 Comparison of the calculated and measured dimensionless scour hole profile
由图8可知,堆石矮堰冲刷坑纵剖面形态与三角形相似,故冲刷面积(As)可表达为冲刷深度和冲刷长度乘积(dsls)的函数:
(12)
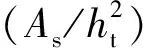
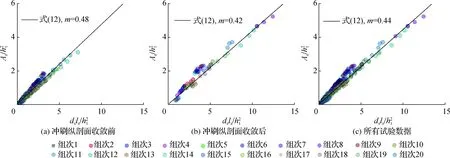
图10 量纲一冲刷面积与对比Fig.10 Comparison of dimensionless scour area
本文提出式(7)—式(12)均基于本文试验结果,适用条件为0.58 本文开展了一系列水槽试验,研究了堆石矮堰清水冲刷历时发展特性,分析了堆石矮堰历时冲刷尺度与水流强度、矮堰淹没度和矮堰透水性之间的量化关系,主要结论如下: (1) 在清水冲刷条件下,堆石矮堰的冲刷尺度在试验初期发展迅速,随后逐渐变缓。 (2) 在冲刷发展的任一时刻,冲刷深度和冲刷长度随水流强度的增大而增加,随矮堰淹没度的增大而减少;矮堰透水性的增大使冲刷长度增加,使冲刷深度减少。 (3) 随着冲刷的发展,堆石矮堰清水冲刷坑纵剖面形态会逐渐收敛,且冲刷坑纵剖面面积与冲刷深度和冲刷长度的乘积线性正相关。 (4) 基于理论分析和试验数据,提出了堆石矮堰历时清水冲刷深度、长度和体积的计算方法,可用于指导堆石矮堰冲刷设计。3 结 论
