沉井在淤泥质土层中的侧摩阻力变化规律研究

郑 蔺，杨开放，韩 治，马 勇，卢国营（中电建路桥集团有限公司，北京 100048）

目前沉井工程作为一项市政公用工程的分项工程已经成熟地应用在各大工程实际施工中。沉井施工更多的是考虑如何下沉、下沉方式的可行性及下沉产生的外溢效应，即有关产生的地基沉降、对周边建构筑物的沉降情况以及沉井的受力计算等。国内外已有的研究集中在对沉井过程中产生的摩擦阻力和地表沉降的监测，并对沉井进行数值模拟分析，以期反映整个施工过程和井壁受力以及对周边环境的溢出影响。辅助沉井方式较为多样，综合来讲主要有三种方法：沉井井壁两侧灌注黄砂法、采用触变泥浆套助沉法以及空气幕助沉法。这三种方法一定程度上都可归为一个原理，即改变沉井侧摩阻力的分布和大小，使得纯粹的滑动摩擦变为滚动摩擦形式，从而将摩擦力降低，沉井能够迅速完成。

1 沉井侧摩阻力研究现状分析

从沉井的侧摩阻力分析入手，研究沉井的摩擦力分布。在国外，英国最早使用了这一技术，在英国伦敦的泰晤士河的沉井采用了对摩擦阻力的分析后[1]，进行完整的下沉施工，并成功竣工，投入市政给排水管道的应用；随后在19 世纪法国开始大规模引入沉井技术，用于箱涵整体下沉等施工场景中；约20 世纪50年代，美国旧金山奥克兰大桥等桥梁建筑开始运用沉井沉箱等方式进行大型跨海大桥的桥墩施工中；日本也对沉井技术有较深入的探索，在第二次大战后至20世纪60 年代初期，日本已经成功运用空气幕助沉技术辅助沉井下沉达156 m。这些沉井技术都在不断突破新的高度和新的建设领域，沉井侧摩阻力的理论探索也在不断深入和实践中。

我国沉井的发展主要在20 世纪初，首先是由詹天佑于1894 年成功用在天津滦河工程上[2]；随后在20世纪30 年代由茅以升建造修筑钱塘江大桥采用了沉井施工技术；国内改革开放以后，大量桥梁的沉井工程涌现，对沉井的技术要求越来越高，这方面的工程师、科学家都在通过各种理论和计算方法来试图找出适合我国工程前沿和施工技术相匹配的沉井技术和设计计算方法及理论模型。力求可以解决工程中沉井突沉或沉井歪斜开裂以及沉井不沉或下沉不均匀等控制困难的技术难题。而实际上，沉井下沉是否能精准，取决于对沉井侧壁的受力分析，其摩擦力的分布情况对下沉有重要影响；由于沉井进入到不同深度时土层物理力学性质不同，对沉井侧壁会带来不同的力学响应。因此，对于侧壁的摩擦阻力的深入分类研究对沉井问题的讨论将有重要指导意义。

2 侧摩阻力计算分析模型

2.1 静止土压计算

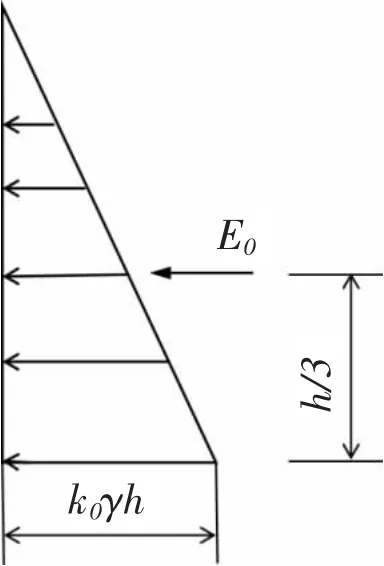
图1 静止土压力计算模型

可以得出，集中力E0的大小为：

通过公式(1)可以将任一沉井进行下土体受荷后荷载集度值计算出来，此计算结果对于分析沉井将采用何种方式进行下沉意义重大。在实际操作中，需要明确土层受影响范围和调整系数的取值，这些经验参数的选取会对最终结果产生一定的波动，有时候波动值的影响是巨大的。

2.2 库伦土压理论

作为实践工程中的土体实际情况，不可能完全处于静止土压的受力状态下，通常会由多方面力效应共同推动形成土体运动。因此，实际沉井过程，土体受压应是多种共同作用，而并非单一土压影响。在库伦理论中，认为土体是一楔形体，该楔形体受力并非只有土压力E；还应有楔形体的自重G 和楔形体的支持力R 的作用。各自作用面与楔形体各边天然呈现某一角度，分别定义为δ 角和φ 角。在各自角度之下形成的楔形体受力状态来表征真实土体受到沉井运动后的力学状态，见图2。

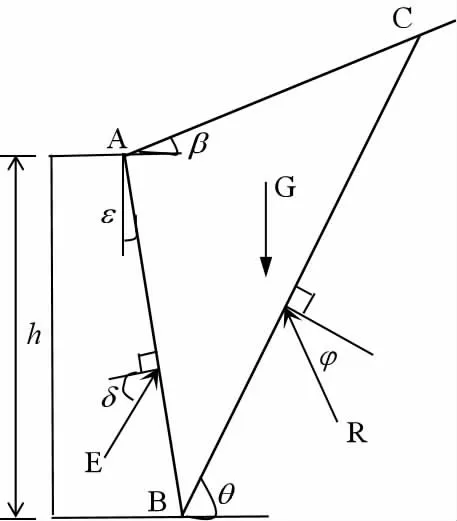
图2 楔形体受力计算模型

根据图2，将土压E 导出得到：

式中：α、θ、β 均为土体与各自作用力所呈角度值；而φ、ε、δ 为土体简化后的楔形体与各边所呈角度。显然公式(2)相比静止土压的公式(1)有更为客观的数学描述，其整体表达式更符合实际工程土体受荷情况，因为天然状态下的土层相对运动与作用力值大小均会呈现一定角度，而并非完整的直接作用。在角度的干扰下，会形成若干不同的应力状态，从而改变沉井井壁与土体之间的摩擦力大小，最终形成不同分布情况的侧摩阻力，形成规律分布态势。

3 工程实例分析

在前述理论计算基础上，通过工程实例来分析说明沉井侧摩阻力的分布规律。选择广东台山污水处理厂站沉井工程进行研究。通过对比验算和侧摩阻力监测，来分析研究侧摩阻力的变化是如何影响沉井效率的。

3.1 土层分析

该项目地处淤泥质土层，淤泥质土体的性质多变，在该土层中施做沉井最为典型。表1 为不同土层物理力学性质分布情况。

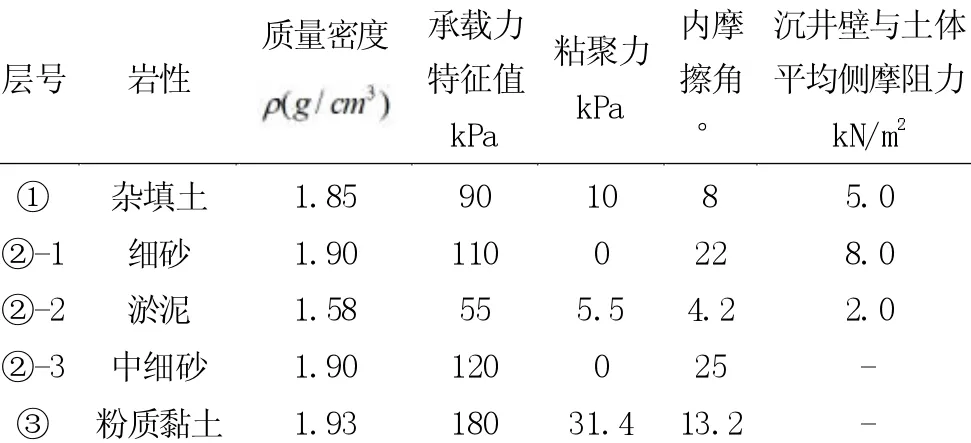
表1 不同土层物理力学性质参数

根据表1 所示，将土层压力经过监测得到不同深度的结果分布曲线，见图3。

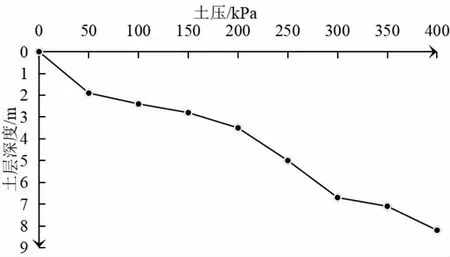
图3 不同土层深度的土压值分布曲线

图3 结果反映出土压在土层越深处，压力值越大。在本工程中，沉井一共下沉至地下9 m，其土压范围从地面的0 不断增大至最底层土体所在的400 kPa左右。由表1 所知，在②-2 土层中，即淤泥质土体中，土压较为稳定，这个特性对于计算和分析淤泥质土层中的沉井施工有重要意义。该结论表明，淤泥质土层虽然承载能力有限，但其压力变化较为固定，研究其分布规律就有了实质作用。同时可以对其土压力和侧摩阻力运用理论基础知识进行一定的数学关系推导，得出一些可用于工程实践的有效结论。

3.2 侧摩阻力分析

在各层面土压下，势必带来沉井井壁的不同侧摩阻力值[4]。该阻力值大小与土压有关。为了准确找出在淤泥质土层中的侧摩阻力变化规律，根据静止土压和库伦土压理论进行计算得到土压力大小，然后由土压值进行侧摩阻力的分析。

沉井在下沉过程中，分别受到水平向的侧向土体压力作用和垂直方向的侧摩阻力作用。显然在沉井开始下沉时，井壁受力状态可用静止土压力来界定并计算；而当沉井不断进行，土体持续受到挤压干扰，静止土压力已不再适用；需考虑库伦土压力做分析[5]。

通过上述分析，土体压力值介于0～400 kPa 之间，为此在淤泥质土层中，选取0～100 kPa、100～200 kPa、200～300 kPa、300 kPa～350 kPa 以 及350 kPa～400 kPa 的5 个区间段进行分析，经过公式(2)的计算，得出图4 所示结果。

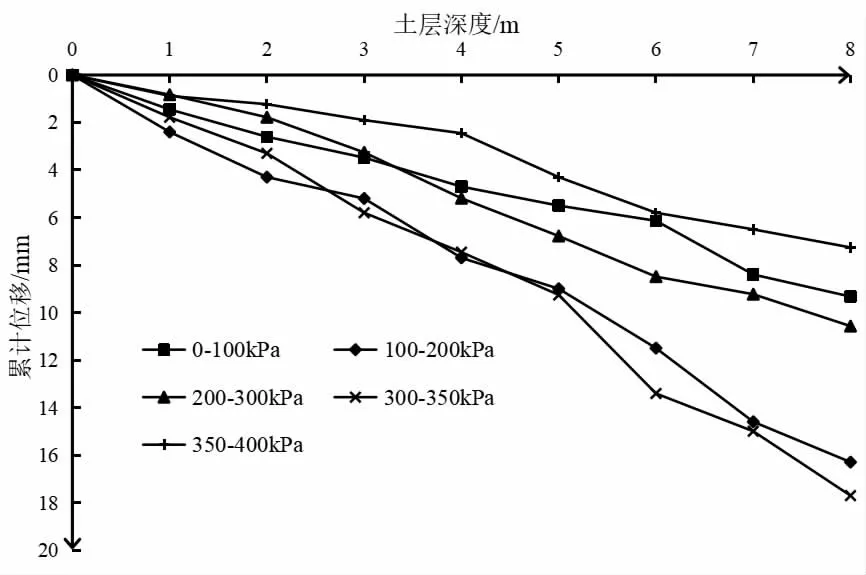
图4 不同土压下的土层深度和位移变化曲线

根据图4 可以看出：在各自不同土压之下，整体位移量随着土层深度而呈现递增趋势，最大可达18 mm。究其原因是土体在沉井进入到淤泥质土中，其粘聚力增大，承载力特征值骤减，通过表1 的土体物理力学性质可知，土体单位承载力特征值仅为55 kPa，在急剧下降的土层中沉入沉井，会使得位移量出现连续增量，因此深度越深，其位移量整体值越大。

此外，在更深层次的土层中，无论土体压力处于何种状态之下，其变化曲线都呈现出先缓后急的态势，这表明：前期沉井的侧摩阻力较大，而随土层深度增加，在不同土压之下的沉井都仅受到较小的侧摩阻力干扰，表现为其位移变化曲线开始出现斜率较大的趋势。由于侧摩阻力减小，沉井切削土体能力增强，不断克服阻力迅速下沉，故在沉井的中后期施工中，尤其容易产生质量问题，如过多下沉、超越设计井底标高、沉井速率过快等。需要工程进行中引起足够重视，防止超沉、过沉等质量问题。

3.3 侧摩阻力计算

基于对侧摩阻力的库伦土压理论的分析已经得到在淤泥土层中的沉井侧摩阻力值和土压变化，进而可以定量研究侧摩阻力的计算问题。沉井从地面开始起沉，会经过多种不同土层的摩擦作用[6]，分别产生不同效果的力学响应。从摩擦角出发，便于找出侧摩阻力的大小变化，在淤泥土层中用φd表示。则淤泥土层中的摩擦角可以表示为：

式中：φ 为实际土压对沉井壁的摩擦角；c 为土体粘聚力；σ 为土体在一点处的正应力值。

通过对摩擦角的分析，可以定量算出侧摩阻力。在此还需引入几个参数，分别是法相土压力强度P；淤泥土层中法向土压力系数Kcn；土层侧壁摩阻力系数Kcf。则可以推导出在淤泥质土层下，侧摩阻力与土压力的数量关系有：

式中：Pn和Pcf是沉井法相土压力和侧壁摩阻力值；γ为土体重度；z 为淤泥质土层厚度，按此计算便可得到完整的沉井侧摩阻力值。由上公式(3)、(4)、(5)可知，实际沉井施工中为较小侧摩阻力对沉井的施工效率影响，应当采取措施，减小井壁与土体之间的摩擦。因为土体摩擦角是既定不变的，与土层所在力学性质有关，能够减少井壁摩擦的只能通过外在干预，如采用两侧阶梯式井壁下沉，并灌入黄砂的方法；亦或者利用压缩空气注入以及打入触变泥浆进行有效减阻，这些方式都可以起到助沉效果，为沉井施工带来实质性便利。

4 结论

本研究从沉井施工的井壁摩阻力问题出发，分析了静止土压力和库伦土压力在沉井施工中的应用方法，并结合实际沉井施工，找处在淤泥质土层中进行下沉井壁的规律性认识，得到不同深度的土压分布、在各自土压范围内土层深度与累计位移的变化关系。最终结合侧摩阻力计算公式推导，得出在淤泥质土层中井壁侧摩阻力的变化规律，并提出实际沉井施工中需特别控制在中后期的下沉控制，以免产生超沉或过沉现象，影响工程施工质量。结合侧摩阻力计算公式，还验证了在沉井施工中，辅助采用灌黄砂、触变泥浆以及空气幕方法都是有效的助井下沉的实用举措，值得在工程实际中予以推广。