基于Abaqus 的土工格栅加筋路堤边坡稳定性分析

2022-09-14韩娜娜

科学技术创新 2022年25期

韩娜娜

（贵州装备制造职业学院，贵州贵阳 551499）

在多山的地区修建高速公路时，因其地貌水文，地形特点等原因，难免会遇到需要填筑的高台路堤或者需要挖除一定深度的路堑情况，这样就会面对一定的难题[1]，如高速公路边坡大变形沉降及坡体的滑落，进而引发高速公路路面的破坏等问题[2]。就目前而言影响土体加筋效果的原因有很多，研究这些原因对于路堤稳定性的影响很有必要[3～5]。本研究主要使用的技术手段为Abaqus 有限元软件建立模型，分别对加筋与未加筋，加筋间距大小建立出相应的模型进行计算分析，最后分别对模拟计算结果作出对应的位移稳性分析。在这里应用强度折减原理计算模型的稳定系数[6]。

1 本构模型的选取

在采用有限元建模进行模拟时，需要对各个单元的构建进行区分材料模拟，对于主要的土体结构而言，由于土体自身结构的特殊性，比如其的多孔非联系性，从力学角度出发又是弹塑性体，同时也是各向异性体，这就导致其内部受力的应力与应变之间很复杂，因此在数值模拟中找到合适的本构模型进行土体的模拟就尤为重要，要在数值模拟中找到一种合适的模型对土体进行模拟就要对比本构模型的理论和本质区别，选择最佳的模型。对于本工程路堤边坡的模拟最佳的选择是Mohr-Coulomb，因为在其对工程中的岩土体进行分析研究时，能够显而易见的反映出土体的内部的塑性区域的变形及土体身的破坏状况，但其也有局限性即缺点，比如在土体破坏前期不能直观的反应其非线性变形特点。

尽管M-C 模型还不能真实的模拟土体反映其变形特征，但是它已经有模拟土体的最佳优点。因此，在综合考虑各方面的影响因素后，本研究选取M-C 模型，来对路堤边坡的稳定性问题进行研究[7～9]。

1.1 屈服面

Mohr-Coulomb 模型采用Mohr-Coulomb 屈服条件，其屈服面函数为

1.2 塑性势面

对于Mohr-Coulomb 模型来说，由于其屈服面上存在尖角的问题，因此在使用流动法则使其塑性势面与屈服面保持一致，就容易出现计算结果不收敛的问题。为了解决这些问题，Abaqus 采取以下方式的塑性势面：

式中：e 为π 平面上的偏心率，它决定了塑性势面的形状，其取值范围为(0.5,1)。

以Mohr-Coulomb 为屈服准则的理想弹塑性模型不能反映加卸载模量的差异和土体的压硬性，因此在做开挖工程时不宜选用，但是在运行计算路堤边坡的强度和稳定性时能使计算结果更加的合理话，因此本研究选用以Mohr-Coulomb 为屈服准则的理想弹塑性模型。

2 数值模型的建立

2.1 基本假定

此模型为理想的弹塑性模型，对于地下水、地表水渗漏、地震荷载、交通荷载、土壤固结、土壤温度敏感性等因素进行忽略，为使模型计算分析更加便捷，现对其作出以下假设。

假设1：填筑的材料表面分布是均匀的，忽略温度影响；

假设2：断面各土层表面是相对水平的；

假设3：用模型计算结果是否收敛来认定模拟的工程是否稳定，如果计算中模型不收敛，无法进行计算，那么说明路堤边坡已经失去平衡而破坏。

2.2 模型的建立

在本模型中，土体使用Mohr- Coulomb 模型，土工格栅所采用的为Abaqus 中的Truss 单元，土工格栅根据其自身只能承受拉力的特性，因此在Abaqus 中的命令中的设置为*No com-pression。土工格栅与土之间的接触使用的命令是Constraints，对于两者之间在力的作用下而相互作用时采用嵌入式来处理，使用Embedded region 嵌入路堤之中，用强度折减原理计算模型的稳定系数，见表1～表2。

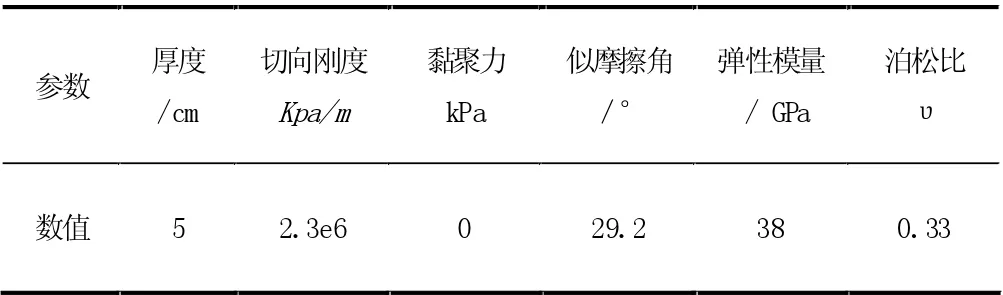
表2 土工格栅参数表

依据某实际高速公路工程路堤边坡工程进行建模，建立与现场相同的断面模型。根据路堤的对称性，选取其中一边的路堤边建模。此工程的边坡形式是两级边坡的形式，边坡中设有2.5 m 的平台，坡比为1:1，根据工程的实际状况，建模时边坡高21 m，破壁为1:1，坡顶的平面为14 m，地基的深度为11 m。主要对路堤截面进行分析，因此使用二维建模即可，建模时模型地基底部完全约束住，左右两边也是水平约束固定，上部是自由活动的，见图1。

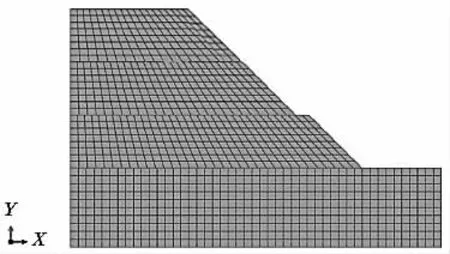
图1 路堤边坡模型及网格划分

3 计算结果分析

3.1 加筋与未加筋路堤变形分析

增大逐渐是增大的，那么路堤在土体的自重下，应力向下传递逐渐增大，在路堤中心处应力达到最大，且向两边逐次递减，在中间边坡处土体的边缘处沉降更大，是因为土体内部相当于有约束限制，土体不同，弹性模量的大小也不一样，自然沉降也有差异。

表3 中的工况四中，加入土工格栅后土体的沉降明显有所减小，整体的分布变化趋势和不加土工格栅时几乎一致，塑性区都是最开始在坡脚处，然后沿着一定角度方向向内延申，最后仅在边坡坡脚处出项部分塑性区，由此可见土工格栅对于分散路堤边坡内部的应力有一定的作用。

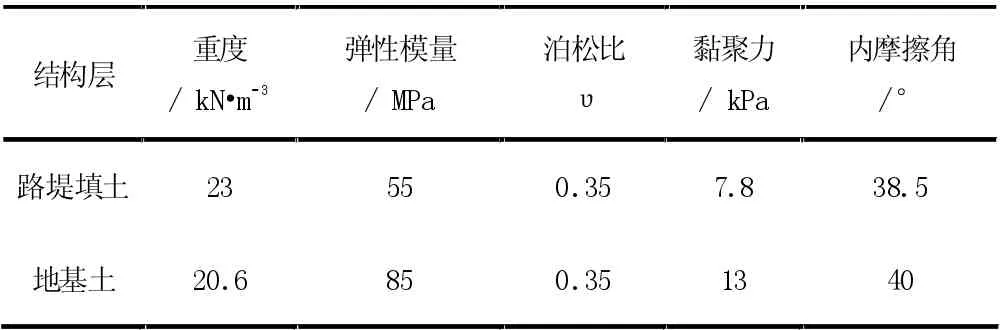
表3 中的工况一结果显示，自重应力随着深度的

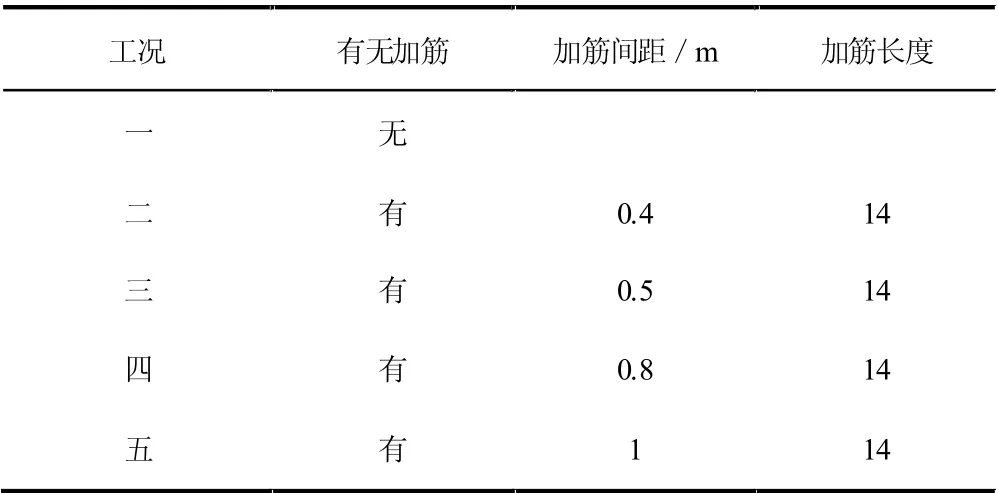
表3 模型计算方案

3.2 不同加筋间距下路堤变形分析

对表格3 中的工况二至工况五进行路堤边坡位移分析。图2～图5 为在相同的折减系数下的4 种不同加筋间距铺设下路堤的塑向及侧向位移。

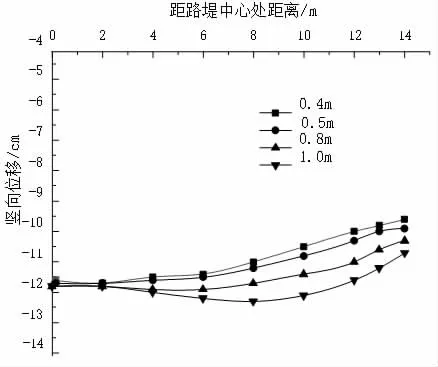
图2 相同折减系数下加入土工格栅后路堤竖向位移

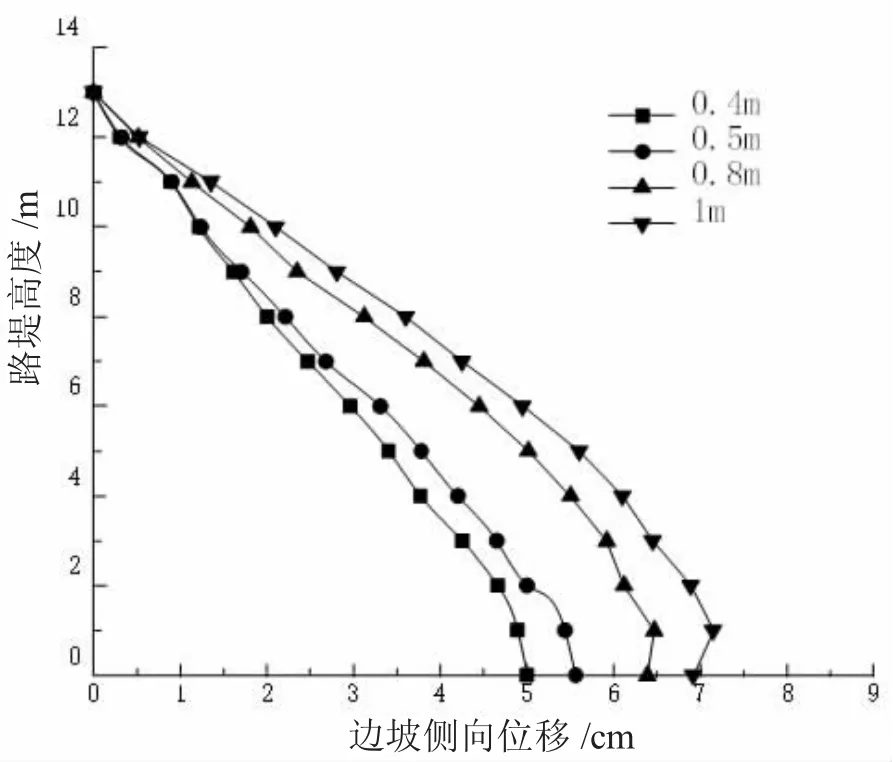
图3 相同折减系数下加入土工格栅后路堤侧向位移

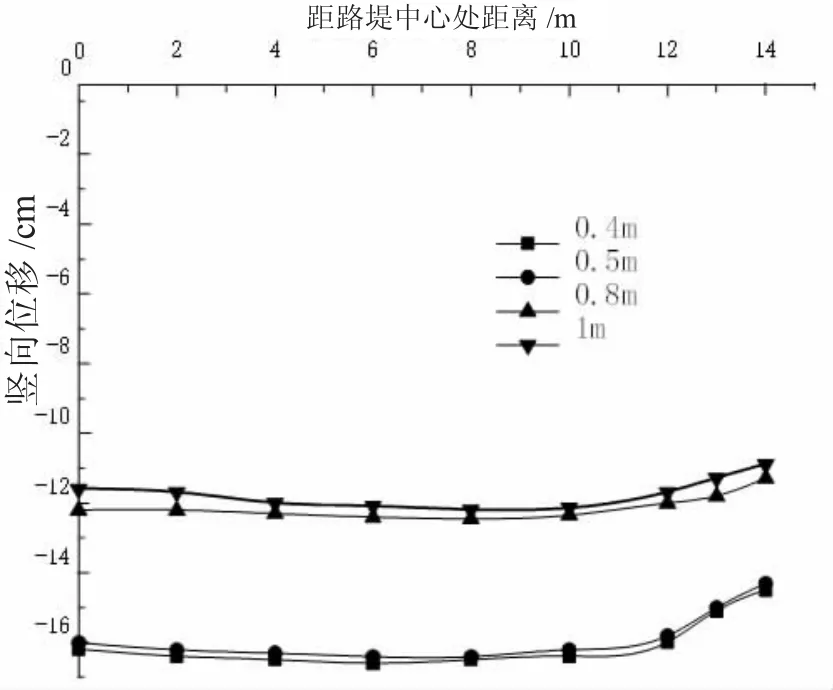
图4 极限状态下加入土工格栅后路堤竖向位移

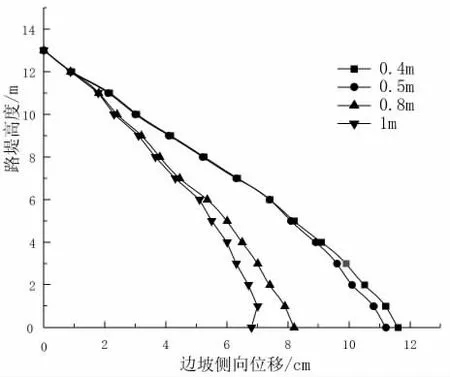
图5 极限状态下加入土工格栅后路堤侧向位移

由图2 可知，路堤的塑向位移，沿着路堤中心处距离总的变化趋势是沉降先变大后变小，在最小的加筋间距为0.4 m 时，路堤的竖向位移总体为最小，为11.7 cm，而当加筋间距最大为1 m 时，最大的沉降变形为12.6 cm，最大和最小加筋间距的沉降减小的幅度为7.7%。

由图3 可知，随着间距的增大，土工格栅路堤边坡的侧向位移沿着路堤中心处逐渐增大，加筋间距为0.4 m，0.5 m，0.8 m，1 m 时所对应的最大位移分别为4.8 m，5.5 m，6.8 m，7.5 m，相应增幅分别为12.4%，16.3%，9.4%，同样减幅亦是如此，由此可知，当加筋间距为0.8 m 时，其效果最好。

在相同极限状态下的加筋路堤沿着路堤中心处的竖向位移，总的曲线变化幅度不大，且0.4 m 与0.5 m 曲线的沉降变化不大，0.8 m 和1 m 的曲线变化也不大，而最大间距和最小间距的沉降变化相差较大，说明在极限平衡状态下，土工格栅间距越小，其所能够负担的变形也就越大。

由图5 可知，不同的加筋间距所对应的边坡的侧向最大位移出现的位置也有所不同，原因是土体加筋间距越小，所使用的格栅越多，使得加筋土体整体刚度越大，变形越小，变形最大位移向外扩散。