基于美团外卖商家选择的一种群体决策方法

彭亚楠, 刘 芳

(1.四川旅游学院 旅游文化产业学院,四川 成都 610100; 2.广西大学 数学与信息科学学院,广西 南宁 530004)

0 引言

随着互联网技术的飞速发展，中国餐饮行业(Online to Offline)的市场规模迅速扩大，许多外卖平台不断涌现出来，例如美团外卖、饿了么、饿了么星选等。基于美团的业务能力和技术已趋于成熟，使得美团外卖在外卖市场上脱颖而出。虽然美团外卖上各种各样的美食满足了不同人的口味，但是同样存在着这样一个问题：当我们在美团外卖上想点某一种外卖时，发现有几家店铺在各方面的条件都比较相近，并且都未曾点过，该选哪一家呢？现在的人们在遇到这类问题时总会纠结，希望能选出最好的。决策问题是我们在现实中最常遇到的问题，利用决策的相关理论知识可以解决一些实际生活中的问题，如文献[1～3]。针对上面的问题，本文建立一个多准则群体决策模型对所要选择的商家进行比较择优，该模型利用问卷调查获得相关因素的权重结果，通过模型对商家进行综合分析，推荐出较好的商家。

1 指标因素及权重值

本文主要以广西南宁市西乡塘区为例，对美团外卖上西乡塘区的232家店铺的所有数据进行取样分析，从中摘取大家比较关注的一些方面作为研究的因素，以调查问卷的方式了解该地区人群对于外卖的一些看法以及对这些因素的重视程度。利用李克特量表对调查问卷选项进行打分，并利用稳定系数法得到人们对这些因素重要性的排序，接着选择比较有差异性的因素计算权重，舍去占比权重很小的若干因素后重新计算，确定了以差评、口味、商家评分、月销售量、配送评分、好评这六个指标因素为研究准则[4]。

利用文献[4]提出的稳定系数法计算出各指标因素的权重为ωC=(0.1752,0.2325,0.1243,0.1005,0.2347,0.1328)。

2 数学模型及算法

2.1 群决策中各因素判断矩阵的构造

在本问题中，利用层次分析法[5～7]的思维方式，决策者根据不同的因素对商家进行两两比较，得到相应的判断矩阵。同时与店铺相关因素的数据相结合，构造一个贴近实际的区间互反判断矩阵。以商家评分C1、口味评分C2、好评数C3、配送评分C4、差评数C5、月销售量C6这几个因素为准则，对商家进行群体决策，选出相对最好的商家来点餐。为了表达方便，所有的因素集F={C1,C2,C3,C4,C5,C6}，将上面的几个因素分为两类，一类是有评分的因素，用FR表示，如商家评分、口味评分、配送评分；另一类是有数量的因素，用FV表示，如好评数、差评数、月销售量。

2.1.1 决策者确定的判断矩阵构造

表1 标度表

2.1.2 商家评分类互反判断矩阵构造

根据美团外卖提供的数据，对于商家评分、口味评分、配送评分这几个因素都是用[0,5]中的数表示，其中5为最高分，在进行数据分析时发现，商家的这些评分主要集中于[2.8,5]内。在这几个因素的准则下，将商店进行两两比较，得到一个互反判断矩阵BFR=(bi)n×n,其中，bij=eFRi/eFRj,FRi表示第i个商家对应FR的评分。由此方法可以构造出互反判断矩阵BC1、BC2和BC3。

2.1.3 商家数量类互反判断矩阵构造

对于好评数、差评数、月销售量这几个因素，在美团外卖等软件上都是以数值表示，虽然好评数和差评数与销售量有关，但是开店的时间对评价条数影响更大，为了减少开店时间不同所造成的差异，同时便于构造互反判断矩阵，我们将通过好评率、差评率、月销售评分来构造判断矩阵。

设Ni为第i个商家的评论总数，Gi为第i个商家的好评数，Bi为第i个商家的差评数，第i个商家的好评率为GRi, 第i个商家的差评率为BRi，其公式为：

(1)

在好评与差评这两个准则下，通过对商家进行两两比较，得到相应的互反判断矩阵。BC4=(bij)n×n为商家在好评准则下的互反判断矩阵，其中bij=GRi/GRj，同样，BC5=(bij)n×n为商家在差评准则下的互反判断矩阵，其中bij=BRi/BRj。

设MSVi为第i个商家的月销售量，为了便于商家两两比较获得互反判断矩阵，我们使用5分制的方法，对需要比较的商家通过以下方法得到一个月销售评分MSVR。

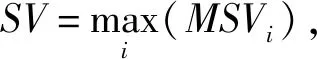
2.1.4 区间互反判断矩阵的构造

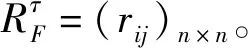
2.2 基于WCR-IOWGA算子的群体决策集结方法

(2)

在不一致性指标的基础上，定义WCR-IOWGA算子[14]

(3)

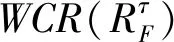
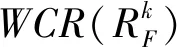
(4)

(5)

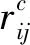
(6)

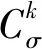
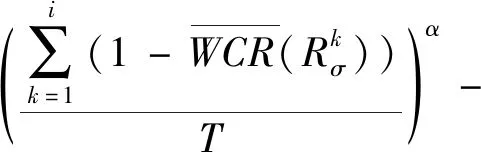
其中

2≤i≤m,0<α<1

(7)

(8)

2.3 模型计算步骤

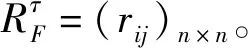
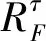
步骤3根据式(7)、(8)，得到与WCR-IOWGA算子相关的指数加权向量。

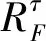
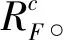
步骤6根据文献[14],得到权重向量

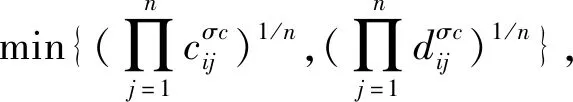
(9)

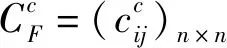
步骤7结合调查问卷分析得到的因素权重，利用式(10)得到每个商家的综合权重。

(10)

步骤8通过文献[15]中的方法得到可能度矩阵P=(pij)n×n。

步骤9利用文献[16]的行列消除方法得到一个排序向量，并按照其分量大小对方案进行排序，得到最优的商家。

3 算例

我们运用上面的模型，解决一个生活中的实际问题。

在广西，螺蛳粉普遍被大家喜欢，美团外卖平台上的螺蛳粉店有很多。现在想要点一份螺蛳粉，在美团外卖上以南宁某大学为派送地，搜到了70多家店，从中选取了三个商家，这三家的起送费、配送费、商品价格、配送时间、包装评分及包装均相同，且无任何满减或折扣。这三家店的商家评分、口味评分、配送评分、好评数、差评数、月销售量这6个因素的相关数据如表2，为保护商家名故以P1、P2、P3表示。有三个决策者对这三个商家进行评价，通过模型构造出区间互反判断矩阵如表3至表5。

表2 店铺数据

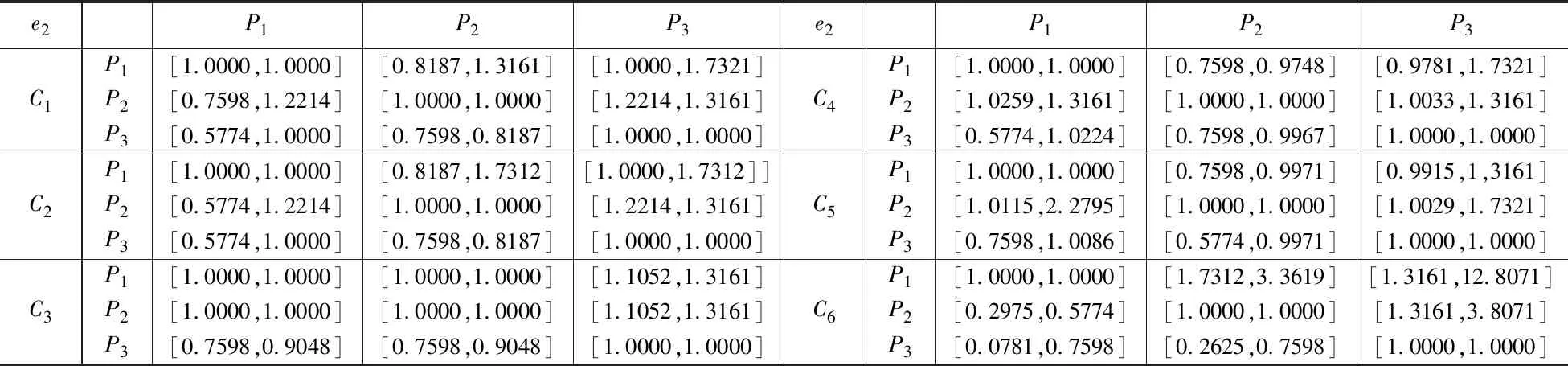
表3 第一个决策者构造的矩阵

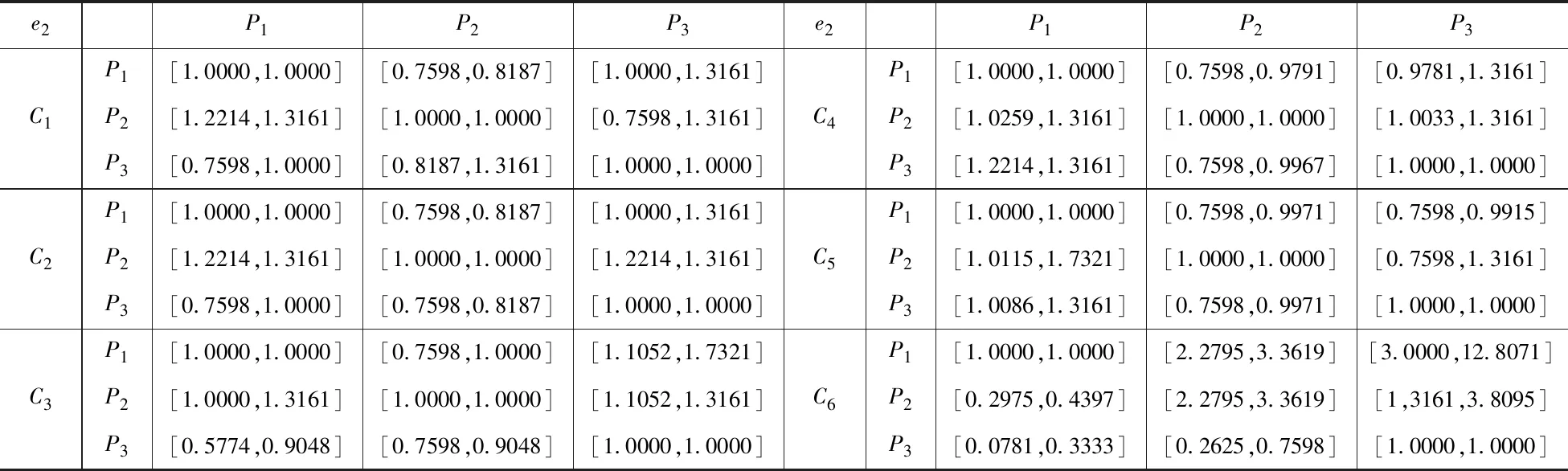
表4 第二个决策者构造的矩阵

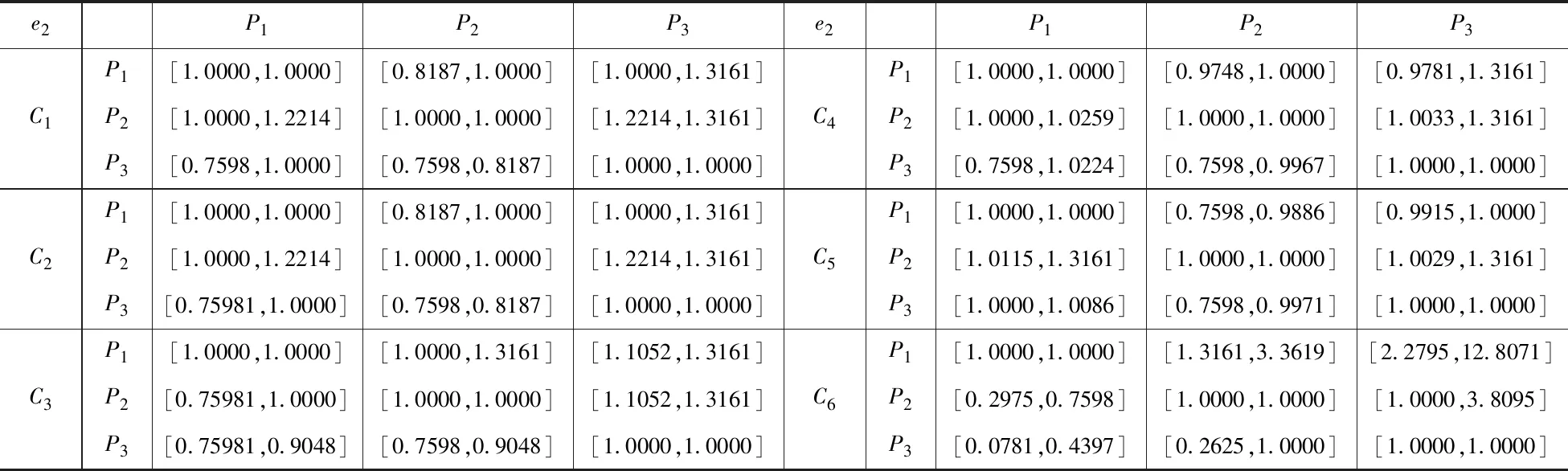
表5 第三个决策者构造的矩阵

vC1=(0.6067,0.1004,0.2929),vC2=(0.4101,0.2970,0.2929)

vC3=(0.6820,0.2224,0.0956),vC4=(0.4025,0.3490,0.2485)

vC5=(0.3740,0.3627,0.2633),vC6=(0.5075,0.3006,0.1919)

利用式(6)，每个因素集成得到综合矩阵如表6，根据式(9)，可获得每个因素的区间权重向量如表7。

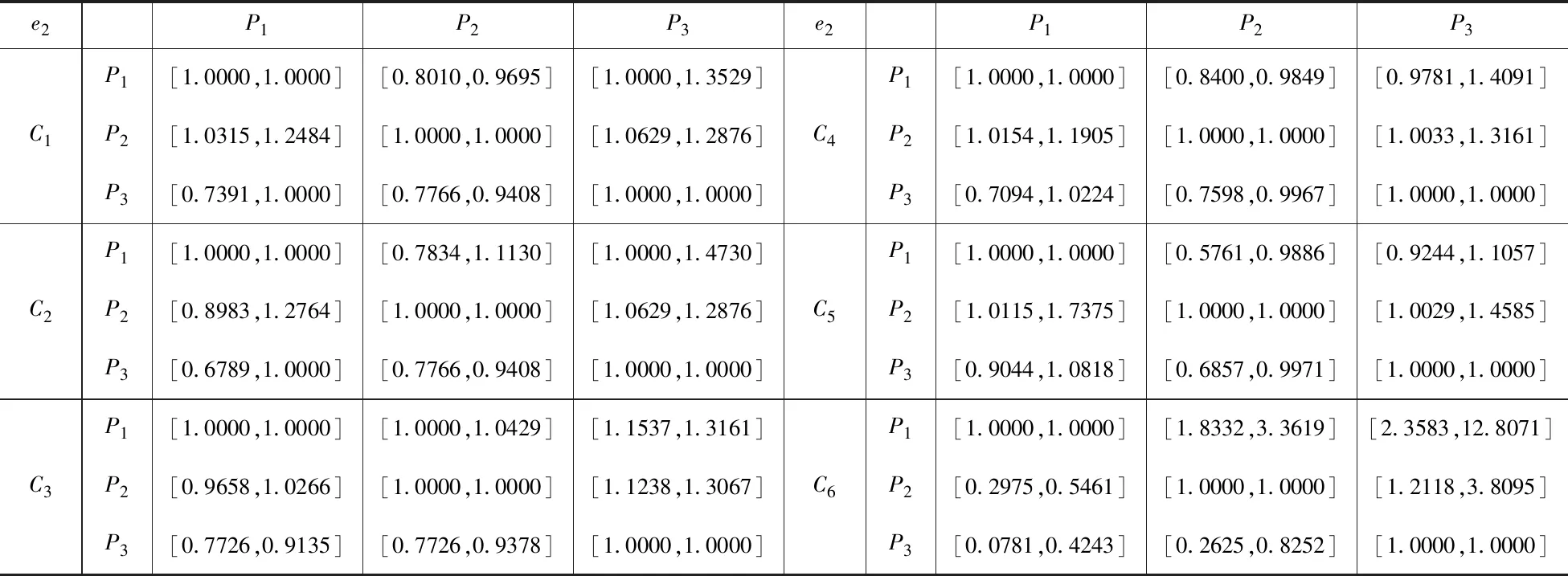
表6 各因素集成得到综合矩阵

表7 各因素的区间权重向量

由问卷分析得到各因素的权重为

ωC=(0.1752,0.2325,0.1243,0.1005,0.2347)

由式(10)得到各商家的综合权重分别为：

ωP1=[1.0413,1.3711]
ωP2=[0.9969,1.1858]
ωP3=[0.777,0.9234]

利用文献[15]得到可能度矩阵

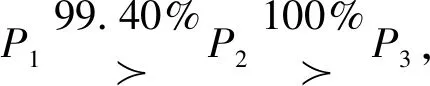
对上述结果进行分析：在一些因素相同的情况下，应用美团外卖在上述三家螺蛳粉店点餐时，更有可能会选择第一家店。比较第一家与第二家店的各项数据，虽然前者店铺的商家评分、口味评分低于第二家粉店，配送评分相同，差评率相近，但是第一家粉店的月销售量却远高于后者。比较第一家粉店和第三家粉店的各项数据，它们的商家评分、口味评分相同，配送评分相近，但是前者的差评率远低于后者，并且第一家粉店的月销售量远高于第三家粉店。

4 结论

本文提出的群体决策方法是在外卖点餐选择商家方法上的一个全新尝试。通过问卷调查得到相关数据，利用稳定系数法对数据进行分析得到相关因素的排序及其权重，从而得到评价商家好坏的相关指标；将商家的数据与决策者的主观意识相结合，给出构造区间互反判断矩阵的方法；基于WCR-IOWGA算子，给出了群体决策集结方法，求得每个准则下店铺的权重，通过一种新方法得到商家的综合权重，最终得到商家的优先顺序，进而根据得到的排序进行选择。