智能制造环境下的备件生产与运输协同调度问题研究

何珮洋, 李昆鹏, 李文莉

(1.华北水利水电大学 管理与经济学院,河南 郑州 450046; 2.华中科技大学 管理学院,湖北 武汉 430074; 3.武汉纺织大学 管理学院,湖北 武汉 430299)

0 引言

作为实施制造强国战略的第一个十年行动纲领，《中国制造2025》重点提到了智能制造，对快速生产和定制化制造提出了更高要求。随着市场竞争的日益激烈，提升供应链响应速度已成为当前备件制造企业赢得客户的关键因素。为了增强备件制造企业的供应链竞争力，智能制造和即时配送的高效协同成为必然趋势。马士华等[1]指出在这种趋势下，未来的工厂将直接建设在物流中心，当产品生产完成后立即通过物流中心配送至客户，这种模式可大大提高供应链整体响应速度。作为世界上最大的快递承运商与包裹递送公司，UPS在智能制造与即时配送领域做了积极尝试，将3D打印生产与自身物流配送相结合，打造定制化生产和即时配送的一体化服务。在智能制造和即时配送高效协同背景下，采用3D打印技术实现备件的本地生产成为现实，越来越多的公司开始将生产中心转移到离客户更近的位置[2]。备件制造企业通过引进大型工业级3D打印设备，采用“随时需要随时生产”的新型备件供应模式，满足客户对备件的个性化需求和高时效性要求。智能制造环境下的备件供应链具有去库存、选址灵活、响应速度快等特点，可有效解决传统备件制造模式下库存压力大、生产成本高、供货周期长等棘手问题。在此背景下，本文以提升基于3D打印技术的备件供应链运作效率为目标，深入研究该新型场景下的备件供应链运作问题。备件制造企业通过线上获得客户订单后，根据客户的订单需求、地理位置、生产资源及运输资源，综合决策各订单对应备件的生产顺序、每个订单分配至哪辆车进行配送、每辆车的出发时间及配送路线。

梳理相关文献发现，由于生产与运输协同调度问题的高复杂性，大多数研究设计启发式算法进行求解。在极少数使用精确算法的研究中，算例求解规模又十分有限。如Chang等[14]设计分支定价算法对并行机生产和多车运输的协同问题进行求解，算例最大规模为5个客户。生产与运输协同调度领域亟需丰富对求解效率更高的精确算法的研究。因此，本文以最小化所有客户等待时间为目标，研究智能制造环境下的备件生产与运输协同调度问题。建立混合整数规划模型，并提出新的集合覆盖模型，该模型能够获得高质量下界；根据问题特点提出协同调度的最优解性质，以便更有效地获得最优解；使用改进的分支定价算法对问题进行求解，并设计新的加速策略和分支策略，使得算例求解规模更大。本文改进的分支定价算法求解技巧可以为其他相关研究提供借鉴，进一步丰富了现有生产与运输协同调度问题的模型和算法研究。

1 问题描述与数学模型

1.1 问题描述

1.2 混合整数规划模型

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Ci+Tnj-Cj≤(1-zij)M,∀i∈V,j∈N

(8)

C0=0

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

xijk∈{0,1},∀i∈V,j∈N,k∈W

(17)

yjk∈{0,1},∀j∈N,k∈W

(18)

zij∈{0,1},∀i∈V,j∈N

(19)

目标函数(1)表示最小化所有客户的总等待时间；式(2)和(3)表示每个客户只能被访问一次；式(4)为流量平衡约束；式(5)(6)确保每辆车从工厂出发，最终又回到工厂且只被使用一次；式(7)为车容约束；式(8)为连续生产两个订单的生产完成时间需要满足的约束；式(9)表示机器从0时刻开始工作；式(10)、(11)和(12)表示订单生产需要满足的约束；式(13)、(14)为车辆服务客户的先后顺序约束；式(15)表示每辆车只有在其配送的订单全部生产完成后才能从工厂出发；式(16)表示若一辆车服务某个客户，则该车需要装载该客户对应的订单；式(17)～(19)为整数约束。优化软件CPLEX可以直接对该模型进行求解，但通过初步试验发现CPLEX的求解能力和效率有限。随着算例规模的增大，使用CPLEX求解器在一定时间内不能得到最优解，甚至无法获得较好的下界。

1.3 集合覆盖模型

为求解上述混合整数规划模型，根据Dantzig-Wolfe分解原理[19]，将其分解为一个结构较为简单但变量数目更大的线性主问题(Linear Master Problem，LMP)和一个具有资源约束的最短基本路径问题(Elementary Shortest Path Problem With Resource Constraints，ESPPRC)。

1.3.1 线性主问题模型

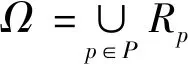
(20)

(21)

(22)

(23)

(24)

xr∈{0,1},r∈Ω

(25)

式(20)为目标函数；式(21)表示每个客户至少被访问一次；式(22)表示每个产品至多被一辆车配送；式(23)表示最优解中至多选择一条加工完成第p个备件的时间节点出发的路径，体现了对生产阶段和运输阶段的协同约束；式(24)是对车辆数的限制；式(25)为0-1变量约束。显而易见，即使对于小规模算例，LMP涉及的可行路径数量就十分庞大。因此，本文使用一种迭代方法——列生成算法，为限制线性主问题(Restricted Linear Master Problem,RLMP)的松弛问题迭代地加入可行列。

1.3.2 满足资源约束的最短基本路径问题

(26)

∀i∈V,j∈N,p∈P

(27)

(28)

(29)

(30)

(31)

(32)

(33)

目标函数(28)表示被选中的弧组成的路径使得检验数值最小；式(29)为车容约束；式(30)表示只有产成品才能被配送，式(31)表示车辆在时刻Tp从3D打印中心出发；式(32)为消除子回路约束；式(33)为0-1变量约束。

2 最优解性质推导

深入分析问题特性后提出最优解满足的性质。

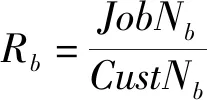
性质1在以所有客户总等待时间最小为目标的单机生产与多车运输协同调度问题中，批次的生产顺序为R1≤R2≤…≤Rb的决策优于其他生产顺序决策。

证明只需证明当CustNb一定时，目标函数与JobNb成正比；当JobNb一定时，目标函数与CustNb成反比。假设存在m个批次l1,l2,…,lm满足CustNl1=…=CustNlm，JobNl1≤…≤JobNlm。当批次的生产顺序为l1,l2,…,lm时，目标函数C1=(T*JobN1*CustNl1+Disl1)+(T*(JobNl1+JobNl2)*CistNl2+Disl2)+…+(T*(JobNl1+JobNl2+…+JobNlm)*CustNlm+Dislm)=TCustNl1*(mJobNl1+(m-1)JobNl2+…+JobNlm)+(Disl1+Disl2+…+Dislm),其中Dislm(1≤w≤m)为批次lw对应的目标函数中运输阶段相应的总时间花费。当批次的生产顺序为除了l1,l2,…,lm外的任一顺序如lm,l2,…,lm-1,l1时，目标函数，C2=TCustNl1*(mJobNlm+(m-1)JobNl2+…+JobNl1)+(Disl1+Disl2+…+Dislm)显然有C1≤C2，因此当CusNb一定时，目标函数与JobNb成正比。同样地，假设存在m个批次l1,l2,…,lm满足CustNl1≤…≤CustNlm，JobNl1=…JobNlm。当批次的生产顺序为l1,l2,…,lm时，目标函数C3=TJobNl1*(CustNl1+2CustNl2+…+mCustNlm)+(Disl1+Disl2+…+Dislm)，当批次的生产顺序为除了l1,l2,…,lm外的任一顺序如lm,l2,…,lm-1,l1时目标函数C4=TJobNl1*(CustNlm+2CustNl2+…+mCustNl1)+(Disl1+Disl2+…+Dislm)，显然有C3≥C4，因此当JobNb一定时，目标函数与CustNb成反比。

3 分支定价算法

3.1 分支定价算法框架

Desrochers等[20]提出的分支定价算法是分支定界算法的一种拓展，它使用列生成在分支的每一个节点处求取下界。在本文改进的列生成算法中，每个列所属的集合Rp(p∈P)体现了该列对应车辆能够进行配送的订单以及车辆的出发时间；每个列中的点序列既包含了客户对应订单的生产顺序也体现了订单的配送顺序。该算法从包含部分列的RLMP出发，根据当前求解RLMP得到的对偶值，通过标签算法求解满足资源约束的最短基本路径问题。如果能够找到检验数值小于0的列，则将该列添加到RLMP中进行重新计算。不断迭代，直至没有检验数值小于0的路径产生，此时得到松弛主问题的最优解。若当前解为整数解，则当前解即为原问题的最优解；否则，利用分支策略对当前非整数解进行分支，求得最优整数解。

3.2 初始解和上界

通过构造简单的启发式算法求得一个可行解，将其作为RLMP的初始上界，并将构成该解的路径作为RLMP的初始列。上界随着分支定价算法的迭代计算不断更新。设计的启发式算法可概括如下：首先随机产生第一个客户点，将其作为第一辆车的第一个访问点。然后寻找距离该客户点最近且未被访问的客户点，在满足车容约束的条件下将其作为该车的下一个访问点，否则由第二辆车进行访问。所有客户点按照上述规则插入车辆，直至所有客户被分配完成。最后对车辆按照性质1进行排序，确定每辆车的出发时间，计算每条路径的时间花费及总目标值。

3.3 动态规划算法

在Feillet等[21]中提到，动态规划算法经常被用来求解ESPPRC。本文设计了一个符合所研究问题特点的动态规划算法——改进的标签法，以此来求解含有生产阶段制约和车容约束的最短基本路径问题。给定一个有向图G′=(P,V,E),p∈P={1,2,…,H}，表示加工完成的第p个备件；顶点集合V={0,1,2,…,n}由3D打印中心和客户点组成；边集合E是图G′中的所有弧集合。

3.3.1 标签定义与扩展

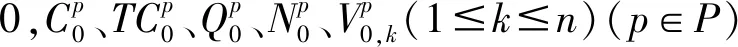
3.3.2 占优原则

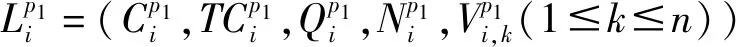
3.3.3 加速策略

根据所研究问题特点，设计两种加速策略来提高列生成算法的求解效率。

使用启发式算法生成高质量路径。参考文献Luo等[23]，通过改进的禁忌搜索算法求解满足资源约束的最短基本路径问题。首先使用当前RLMP最优解中的基变量作为禁忌搜索算法的初始路径，然后将进行禁忌搜索后目标检验数小于0的路径添加到当前主问题中。本算法使用了三种邻域结构，分别是(a)“加”操作：在当前路径中添加一个客户点；(b)“删除”操作：在当前路径中删去一个客户点；(c)“交换”操作：当前路径中的一个客户点和非当前路径中的一个客户点进行交换。在保证p相同的情况下，每一种邻域结构均能产生相应的邻域解。

3.4 分支策略

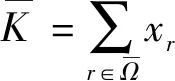
4 算例与结果分析

本实验的计算机参数配置为Intel(R)Core(TM) i5-2400S CPU @ 2.50GHz 2.50 GHz。

4.1 数据生成

本文实验数据是基于CVRP经典数据集(来源http://vrp.atd-lab.inf.puc-rio.br/index.php/en/)进行修改，以生成符合本文研究问题特征的数据，具体做法如下：3D打印中心和客户点坐标均从A组算例中随机选取；由于本文研究问题是基于备件制造行业，客户需求量有限，每个客户所需备件数为[1,5]之间的随机数；为了方便计算同时不失一般性，单位产品的生产时间设为2。

4.2 计算结果与分析

4.2.1 模型及算法的验证分析

为了评估模型正确性和算法有效性，使用CPLEX求解器IBM ILOG CPLEX12.2对小规模算例进行求解，将CPLEX求得的全局最优解或当前上界与分支定价算法所得结果进行对比。选取5组不同规模的算例进行测试，n为客户和工厂总数。在前四个算例和第五个算例中车辆数分别为2和3。算例9和10中“-”表示CPLEX在显示的求解时间内没有求得最优解，只有相应的上下界。由表1可知使用CPLEX求解器与分支定价算法求得的结果吻合，验证了模型正确性和算法有效性；通过两者求解时间对比体现了改进分支定价算法的高效性。

表1 CPLEX与改进分支定价算法求解小规模算例的结果对比

4.2.2 较大规模算例结果

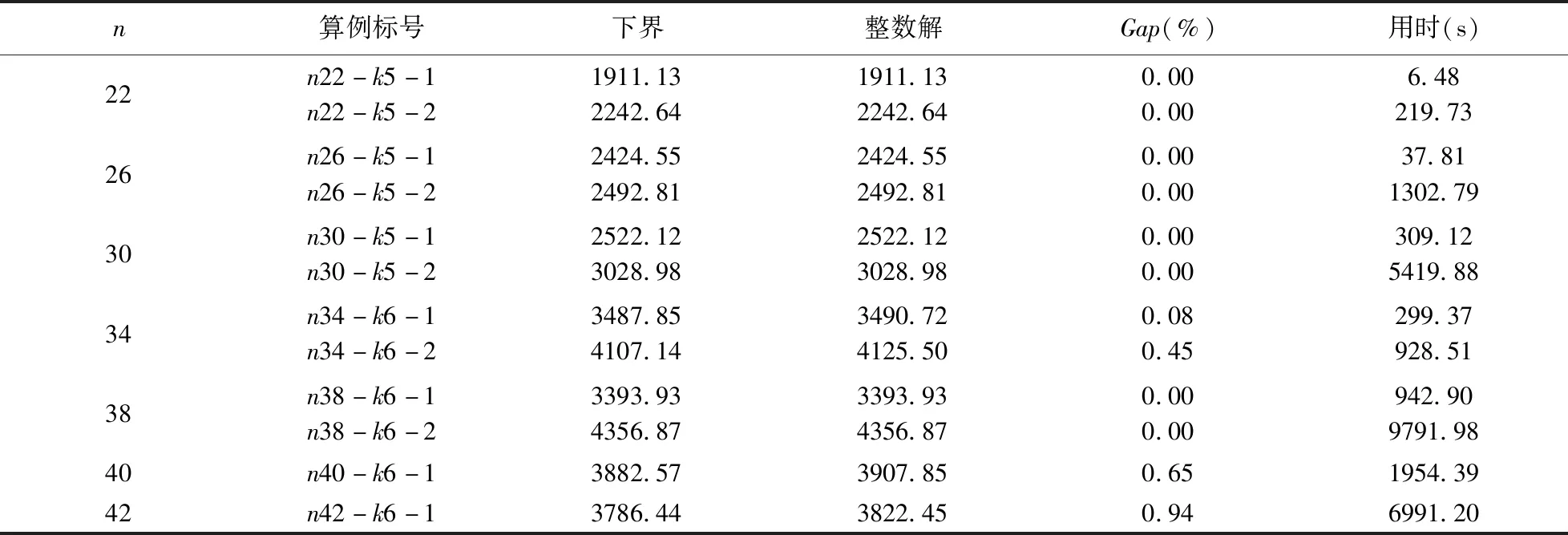
表2 较大规模算例结果

4.2.3 加速策略效果分析

为了证明本文所设计加速策略的有效性，分别给出不使用任何加速策略、仅使用最优解性质加速策略、仅使用启发式加速策略以及同时使用两种加速策略对不同规模算例的求解时间。n表示客户和工厂总数，由表3可知，两种加速策略均具有较为显著的加速效果，特别是当两种加速策略同时使用时，加速效果最为显著，平均求解时间由528.28s缩短为270.51s，求解效率提高了48.79%。

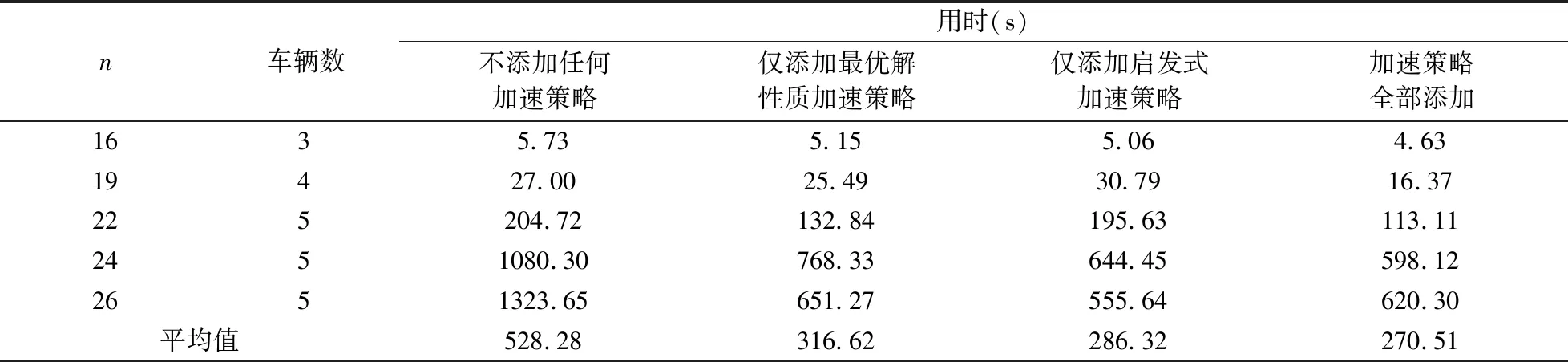
表3 加速策略效果对比

5 结论

智能制造和即时配送环境下的备件生产与运输协同调度问题研究对实现制造强国具有重大意义。在此背景下，本文以提升基于3D打印技术的备件供应链运作效率为目标，研究了智能制造环境下的备件生产与运输协同调度问题。建立了协同调度的混合整数规划模型和集合覆盖模型。深入分析问题特性后，提出最优解性质，使用改进的分支定价算法进行求解，并设计了新的加速策略和分支策略，使算例求解规模更大。多组算例测试结果表明，所得整数解与下界Gap均不超过1%，可知所构建模型和算法能够获得高质量解、所建立集合覆盖模型能够提供高质量下界，有效解决了智能制造环境下较大规模的备件生产与运输协同调度问题。有效帮助备件制造企业在实际生产和运输环节进行协同决策，极大提升了备件供应链的响应速度。

进一步研究可考虑生产阶段使用并行机生产、运输阶段使用不同车型车辆进行配送的情况，在丰富问题特性的同时探索更高效的精确求解算法。