加权Markov修正模糊信息粒的电力负荷区间预测
2022-09-13童林何青青
童林, 何青青
( 六盘水师范学院 物理与电气工程学院, 贵州 六盘水 553004 )
0 引言
电力系统的短期负荷预测对智能电网的构建、电力的生产计划、发电机组的优化调度等具有重要意义[1].近年来,随着机器学习理论的不断发展,一些机器学习方法被应用于电力负荷预测.例如:文献[2]和[3]提出了一种基于智能算法改进的BP网络(back propagation,BP)的电力负荷预测方法,该类方法虽具有建模简单和训练时间短等优点,但仍然存在算法易早熟收敛以及误差平方和容易导致出现局部极小点等问题[4].文献[5]提出了一种基于支持向量机(support vector machine, SVM)的电力负荷预测模型,该模型虽然可实现电力负荷的高维空间映射和预测,但在参数选择方面需进一步优化,且使用优化算法优化SVM参数过程中存在容易陷入局部最优和早熟等问题[6].文献[7]提出了一种使用长短时记忆(long short - term memory, LSTM)网络对区域电力负荷进行预测的方法,该方法虽具有较高的预测精度,但在负荷变动较大时预测精度降低.
由于使用预测模型对时间序列数据进行预测均会产生一定的误差,因此一些学者提出了一些修正误差的方法.例如:文献[8]提出了一种基于误差修正的光伏预测方法,该方法虽考虑到了光伏出力预测误差,并基于Copula理论和k均值聚类算法对光伏预测值进行了修正,但存在k值选择困难、计算复杂等问题.文献[9]和文献[10]的作者分别利用不同的误差修正函数对风电功率进行了预测,这2种函数虽然可实现对预测误差的补偿与修正,但由于这2种函数使用固定的修正因子使得其缺乏良好的泛化能力.上述预测方法都是对电力负荷点值进行预测的,而研究[11]显示采用区间预测技术可以更好地反映输出功率的波动性和随机性.基于上述研究,本文针对单一负荷定量预测模型不能表征预测结果和预测电力负荷波动范围精度较低的问题,提出一种基于加权马尔可夫(Markov)修正模糊信息粒的电力负荷区间预测模型,并通过实例分析验证了本文方法的有效性.
1 模型描述
加权Markov修正模糊信息粒的电力负荷区间预测修正模型的结构见图1.为便于表述,本文在下文中将电力负荷简称为负荷.
负荷区间预测修正模型主要分为3个部分:
1)电力负荷模糊信息粒化(fuzzy information granulation, FIG)部分.该部分的主要功能为:获取负荷模糊信息粒,划分FIG窗口;选择隶属度函数,计算隶属度函数参数;对细颗粒度下的负荷数据进行FIG操作,提取各窗口内模糊粒的有效信息;确定负荷的合理区间上界(Up)、下界(Low)及趋势值(R).
2)电力负荷预测部分.该部分的主要功能为:建立基于LSTM的负荷预测模型,优化LSTM网络参数;获取负荷模糊信息粒的Up、Low及R的预测值及其与实际值相减所得的误差值;提取Up、Low及R的各阶自相关系数,确定下一部分的输入参数.
3)误差修正部分.该部分的主功能为:建立加权Markov修正模型,计算负荷误差转移概率和修正后的预测值.

图1 电力负荷区间预测修正模型
需要说明的是,图1中出现了两次基于LSTM的负荷变量预测值,但每次出现时其具体用途不同,其中与实际值相连接的预测值是用于计算Markov链状态转移概率矩阵,与Markov修正相连接的预测值是用于计算最终的修正量.
2 负荷区间预测模型
2.1 负荷模糊信息粒化模型
1997年Zadeh[12]首次提出了信息粒化模型,该模型可用以处理相似度较大或难以区分的数据,且便于研究信息的形成、表示、粗细及语义解释等.信息造粒方法主要有模糊集方法、粗糙集方法及商空间方法.由于基于模糊集方法的信息造粒模型能够准确反映事物特性和划分复杂多变的电力负荷数据[13],因此本文将该模型作为信息粒化的工具.负荷时间序列FIG的建模主要分为如下两个步骤:
1) 划分原始数据的窗口.划分数据窗口的目的是简化数据序列,进而便于粒化研究.划分数据窗口的方法是在数据序列上选择合适的窗口(即子间隔)大小进行划分.为使每个窗口具有相等的粒化数目,本文将时间窗口设为固定值.假定负荷时间数据序列为X=(x1,x2,…,xn), 定义k(1≤k≤n)为划分的窗口数量,则负荷的具体粒化过程可表示为如图2所示的流程.图2中,负荷时间数据共被划分为k个窗口,每个窗口的粒化数目为n/k.
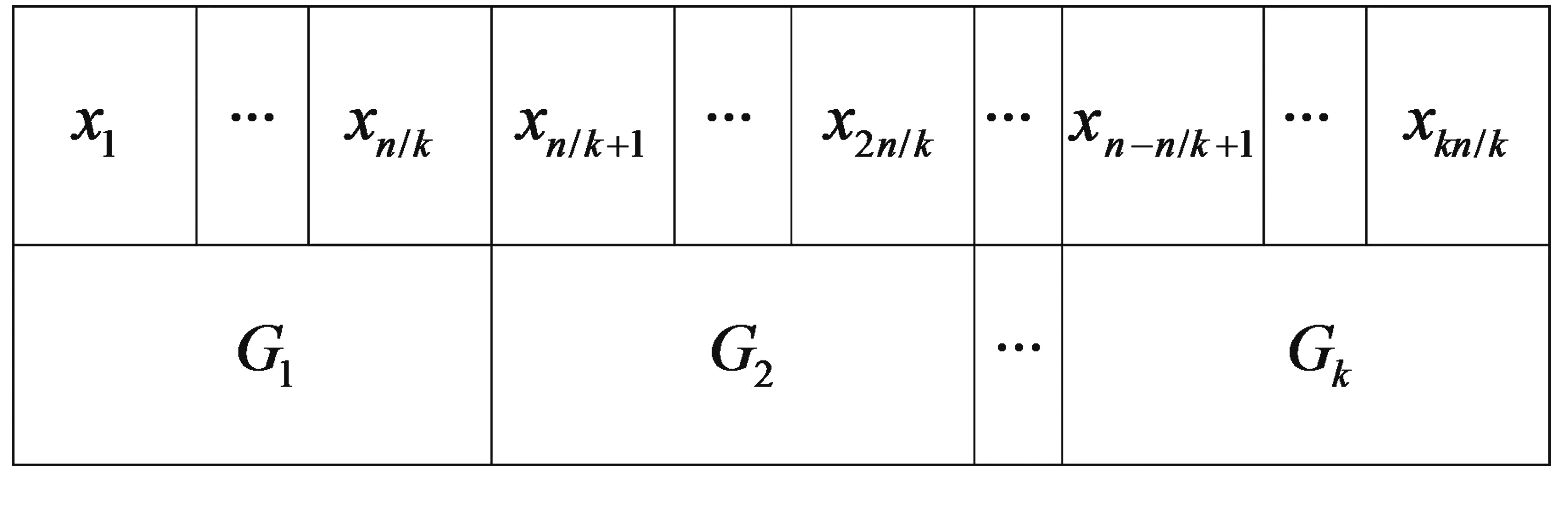
图2 负荷时间序列的FIG流程图
2) 选择隶属函数.选择隶属函数的目的是表征图2窗口中的数据,进而选择合适的信息粒度刻画规则.由于三角型隶属函数具有构造简单和应用范围广的优势,因此本文采用该函数确定负荷的合理区间.三角型隶属函数的表达式为:
(1)
式中,x为模糊论域中的变量,a和c分别为模糊上界和模糊下界,b为模糊核参数.假设已知单个窗口由N/K个连续点{x1,x2,…,xN/K}组成,且这些点按升序排列.数据点{x1,x2,…,xB}位于模糊集的左侧边界,剩余点位于右侧.本文参考文献[14]中的方法计算a、b和c的参数.
计算Q(a) 的公式为:
(2)
计算Q(a)导数的公式为:
(3)
当Q(a)的导数为0时,a为:
(4)
计算Q(c)的计算公式为:
(5)
当Q(c)为最大值时,c为:
(6)
上述公式中,核参数b的取值为:
(7)
2.2 LSTM模型
LSTM网络是一种时间循环神经网络,它不仅能降低发生降梯度消失或梯度爆炸的风险,还能够较好地保持长时间记忆.LSTM网络主要包括输入门it、 遗忘门ft和输出门ot[15], 具体结构如图3所示.遗忘门的功能为通过读取LSTM网络的上一层输出ht -1和当前层输入xt来选择LSTM网络丢弃的信息,其计算公式为:
ft=σ(Wf·[ht -1,xt]+df).
(8)
式中,σ为激活函数,Wf为遗忘门的权重系数,df为遗忘门的偏置项.

图3 LSTM网络结构图

it=σ(Wi·[ht -1,xt]+di),
(9)
(10)

ot=σ(Wo·[ht -1,xt]+do),
(11)
(12)
式中,Wo为输出门的权重系数,do为输出门的偏置项.
3 加权Markov修正模糊信息粒模型
Markov模型可根据系统当前状态推测下一时刻的概率分布,对预测的偏差值具有良好的修复功能,因此本文将该模型作为修正LSTM预测误差的工具[16].构建加权Markov修正模型的具体过程为(以未经过模糊粒化的负荷数据X=(x1,x2,…,xn)为例)[17]:
1) 计算Markov自相关权重.根据负荷序列的自相关系数计算Markov自相关权重,其计算公式[18]为:
(13)

2)状态区间的划分.状态区间的划分方法是将实际值与预测值之间的误差序列δ(0)={δ(0)(1),δ(0)(2),…,δ(0)(n)}划分为E1,E2,…,Em等状态区间,其中的任意区间可表示为:
Ei∈[ei -1,ei],i=1,2,…,m.
(14)
其中,ei -1和ei分别为第i个误差状态区间的下限值和上限值.
3) 计算状态转移概率矩阵.当发生误差状态转移的总数目为Ei, 由误差状态Ei经过1步转移到误差状态Ej的数目为Mij时,此时误差状态转移概率为:
(15)
由m×m组转移概率得到的1阶误差状态转移概率矩阵为:
(16)
由P(1)可得l阶误差状态转移概率P(l)为[P(1)]l.
4) 计算状态转移加权向量矩阵.首先通过状态转移概率矩阵获取状态转移概率矩阵初始状态对应的行向量以及通过现有状态获取新的概率转移矩阵,然后对新概率转移矩阵中的i列向量加权求和,并以其作为最终的预测概率Pi, 即:
(17)
式中,θl为根据各阶自相关权重计算得到的加权系数,其计算公式为:
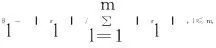
(18)
式中,l为阶数.根据式(17)得到Pi后,将max{Pi,i=1,2,…,m}所对应的状态i作为预测值所处的误差区间Ei∈[ei -1,ei].

(19)
利用修正系数计算预测值x的公式为:
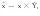
(20)
4 算例分析
4.1 实验准备
选取2010年12月份澳大利亚某地区的负荷集作为实验数据来验证本文所提模型的有效性,其中将1日至28日的负荷作为训练集,将29日、30日及31日的负荷作为预测集,数据间隔时间为0.5 h.另外,取29日和30日的负荷数据用于建立加权Markov模型,并使用加权Markov模型对31日的负荷数据进行修正.选取均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)作为评判指标,各指标的计算公式为:
(21)
(22)
(23)
式中,n为数据量,x为实际负荷值,x*为预测负荷值(修正值也视为最终预测值).
4.2 实例分析
4.2.1预测值的对比分析
首先对负荷进行FIG操作(选择粒化窗口数为6, 即将24 h的数据粒化为8个窗口),由此得到的29日、30日及31日的粒化结果(共24组)见图4.
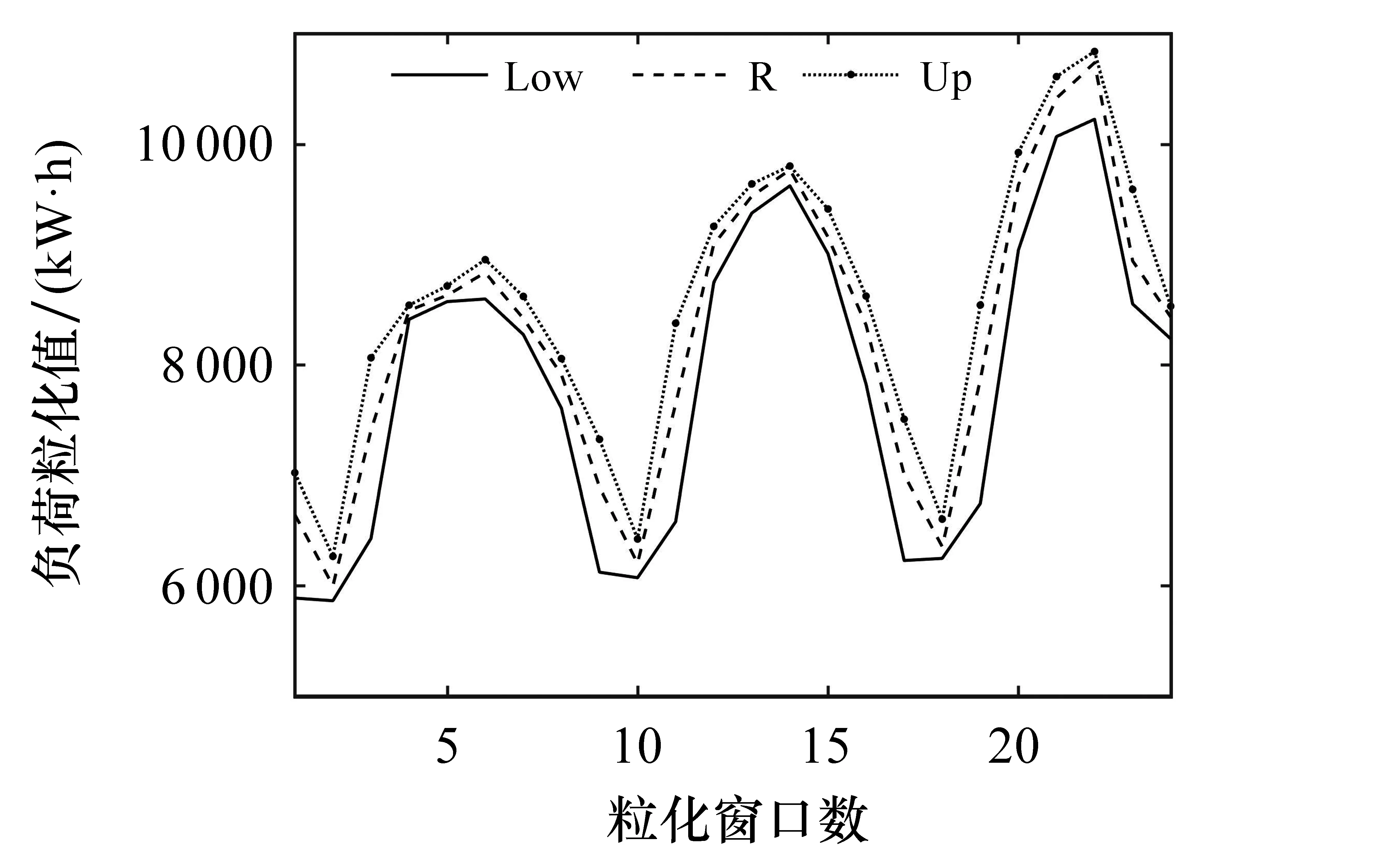
图4 负荷信息粒化结果图
由图4可以看出,经过FIG操作后,负荷分解为3种模糊信息粒(Low、Up和R).本文通过计算Low、R和Up 3组预测数据的整体RMSE、MAE及MAPE来评价预测模型的性能.计算过程为首先分别计算Low、R及Up的RMSE、MAE及MAPE,然后取RMSE、MAE及MAPE的平均值.具体的计算公式为:
(24)
(25)
(26)
4.2.2加权Markov修正计算及其结果分析
由于对基于FIG - LSTM获得的预测值进行加权Markov修正时数据组数过多,因此本文在此仅以Up值为例给出计算过程.获得Up值后,按照相对误差值的大小对其排列,并将其划分为如下4种状态:E1∈[95.53%,97.84%),E2∈[97.84%,100.15%),E3∈[100.15%,102.46),E4∈[102.46%,104.77%).
根据上述原始数据序列,利用式(13)计算出的各阶的自相关系数分别为0.713 0、0.299 6、0.001 9、-0.147 5, 由此绘制出的各阶自相关系数图如图5所示.由图5可知, 1阶和2阶的自相关系数较高,故本文计算加权Markov模型取1阶和2阶.
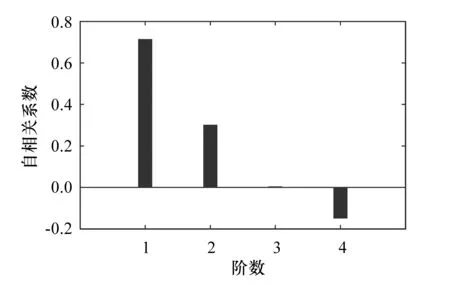
图5 各阶自相关系数图
由E1、E2、E3及E4状态区间分类中获得的29日和30日各个时段的状态区间分类情况如表1所示.
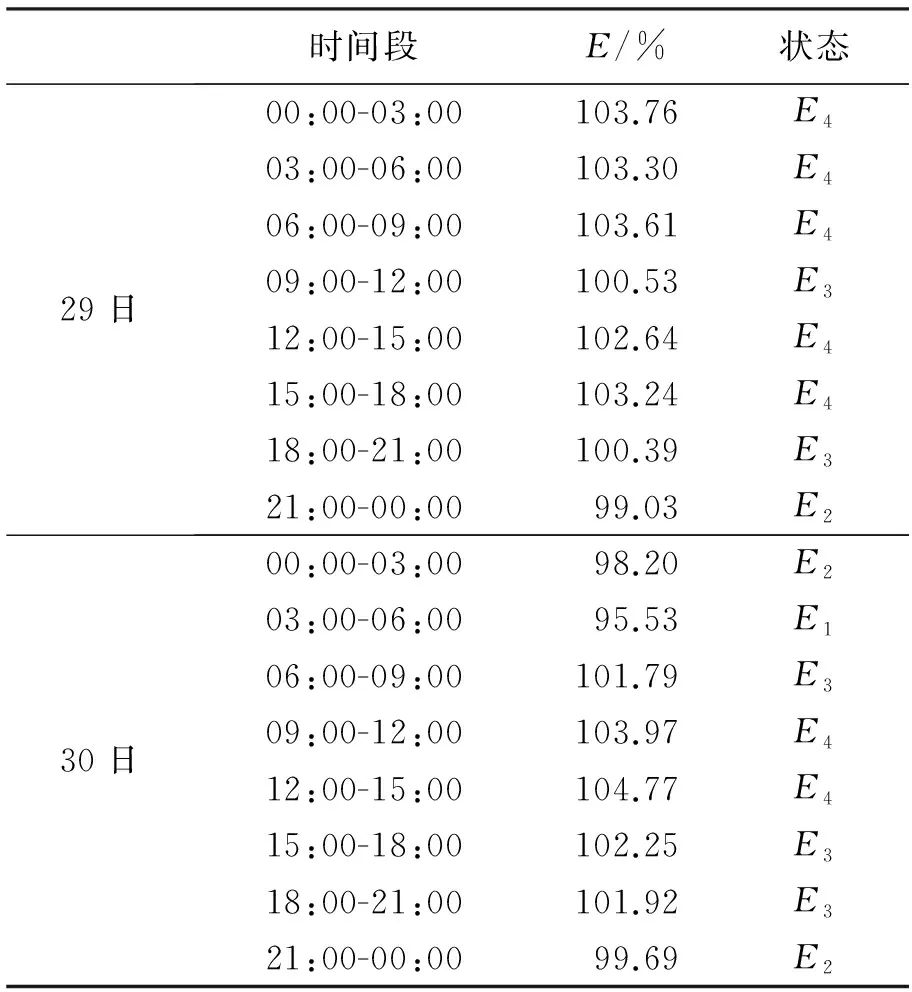
表1 误差状态划分
根据式(18)计算1阶和2阶的权重,得:
为预测31日的Up值,首先需计算各阶下的Markov转移概率矩阵,计算得:
由表1可知,预测的Up值在30日的21:00-00:00和18:00-21:00时间段内分别处于E2和E3状态.根据Markov转移概率矩阵可得, 1阶转移概率向量取(0.500,0.500,0,0), 2阶转移概率向量取(0.200,0.280,0.212,0.308).由式(17)计算出的加权Markov预测概率见表2.
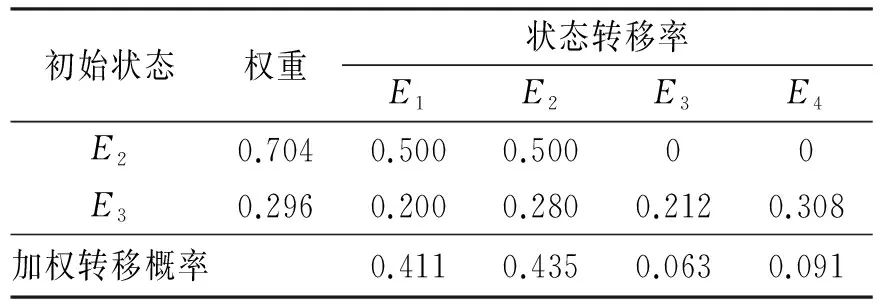
表2 加权Markov转移概率

根据式(20)对预测值x进行修正计算得:
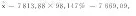


表3 负荷模糊信息粒的预测结果 kW·h
由表3可以看出,利用加权Markov修正的预测值更接近于真实值.由于仅通过表3无法判断加权Markov模型精度的提升效果,本文利用式(24)、(25)及式(26)计算了2种模型的整体预测性能,结果如表4所示.由表4中的指标可知,本文提出的Markov - FIG - LSTM模型的RMSE、MAE和MAPE指标比FIG - LSTM模型分别降低了4.78%、11.37%和11.72%,这表明加权Markov能够更好地对LSTM预测误差进行修正.
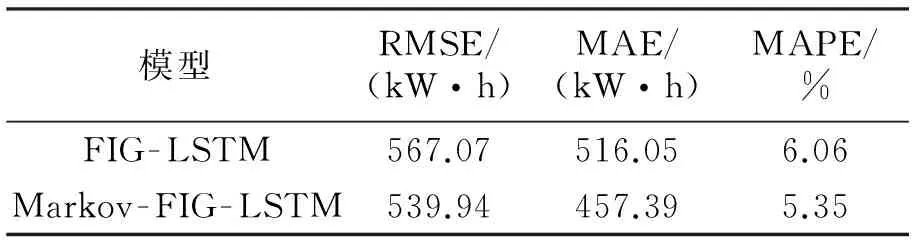
表4 FIG - LSTM模型和Markov - FIG - LSTM模型的整体预测性能
5 结论
研究表明,本文提出的Markov - FIG - LSTM预测方法比FIG - LSTM预测方法能更好地预测电力负荷区间,因此本文方法能够为电力负荷调度及电网分析提供更有力的依据.在今后的研究中我们将采用迁移学习等方法来进一步改进模型,以实现小样本下的电力负荷高精度预测和提高本文方法的适用性.
