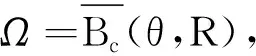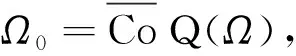Banach空间中分数阶微分方程Robin边值问题解的存在性

李小龙

( 陇东学院 数学与统计学院， 甘肃 庆阳 745000 )

分数阶微分方程在流体力学、分数控制系统与分数控制器、电分析化学、神经的分数模型以及分数回归模型等领域有着广泛的应用.近年来,许多学者应用锥拉伸与锥压缩不动点定理、Lexar - Schauder不动点定理及上下解的单调迭代技巧等研究了分数阶边值问题解的存在性[1-7],但在一般的无穷维Banach空间中对该类问题的研究还比较少[8].与普通微分方程相比,研究Banach空间微分方程的最大难点是把微分方程转换为与之等价的积分方程后，相应的积分算子不再具有紧性.2011年,文献[5]的作者在实数空间中运用锥拉伸与锥压缩不动点定理讨论了非线性分数阶微分方程边值问题(式(1))解的存在性.

(1)

(2)

1 预备知识

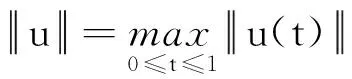
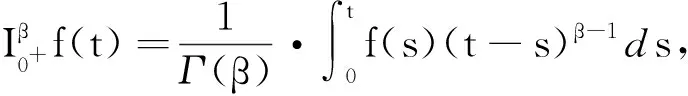
定义2[1]设β>0, 函数f:(0,+∞)→R的β阶Riemann - Liouville导数为

其中Γ(·)为Gamma函数,n=[β]+1.

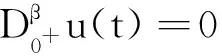
引理2[2]假设u∈C(0,1)∩L(0,1)有β>0阶导数属于C(0,1)∩L(0,1), 则

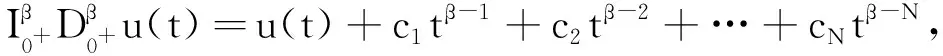
其中ci∈R,i=1,2,…,N(N是大于或等于β的最小正整数).

引理3[8]设1<β≤2, 则对∀h∈C(J,E), Banach空间E中的线性分数阶边值问题

存在唯一解：

(3)

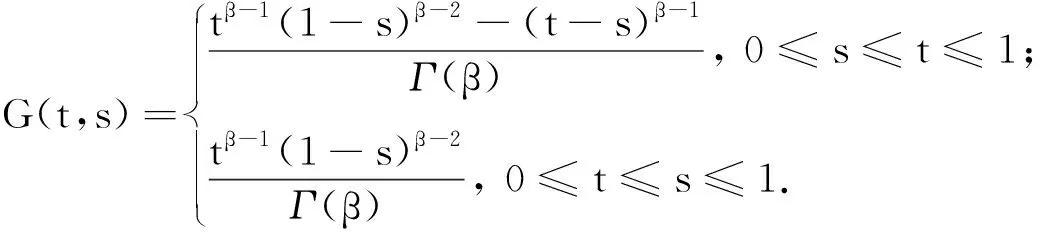
本文中，E与C(J,E)中的有界集的Kuratiwski非紧性测度均由α(·)表示.对B⊂C(J,E), 记B(t)={u(t)|u∈B}⊂E,t∈J.

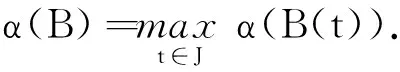
引理6[9](凝聚映射的Leray - Schauder不动点定理) 设E是Banach空间,Q:E→E凝聚,若集合{x∈E|x=λQx,0<λ<1}有界,则Q在E中必有不动点.

引理7[9](Sadovskii不动点定理) 设E是Banach空间，D⊂E为有界凸闭集,若Q:D→D凝聚,则Q在E中必有不动点.

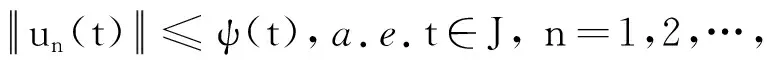
引理9[11]设D⊂E有界,则存在D的可列子集D0， 使得α(D)≤2α(D0).

定义算子Q:C(J,E)→C(J,E)为：

(4)

则Q:C(J,E)→C(J,E)连续,且边值问题(2)的解等价于积分算子Q的不动点.

2 主要结果及其证明

定理1设E为Banach空间,f:J×E→E连续.边值问题(2)至少存在一个解,若f满足以下条件:

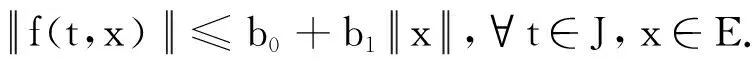
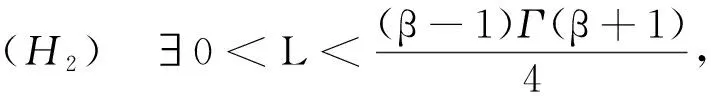
证明由式(4)可知Q:C(J,E)→C(J,E)连续.下证由式(5)定义的算子Q:C(J,E)→C(J,E)为凝聚映射.由条件(H1)知,Q将C(J,E)中的有界集映为有界的等度连续集.为证明α(Q(B))<α(B), 任取C(J,E)中非相对紧的有界集B.对于C(J,E)中的有界集B, 由引理9知其存在可列集B1={un}⊂B, 使得α(Q(B))≤2α(Q(B1)).故对任意t∈J, 由引理8及条件(H2)可得：

下证Ω={u∈C(J,E)|u=λQu,0<λ<1}是C(J,E)中的有界集.事实上,对∀u∈Ω， 根据算子Q的定义有：

(5)

对式(5)两边取范数并结合条件(H1)可得：

(6)

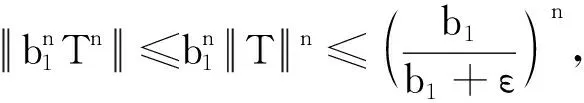
定理2设E为Banach空间,f:J×E→E连续.边值问题(2)至少存在一个解,若f满足定理1中的条件(H1)及如下条件(H3):

证明由条件(H1)知,Q把C(J,E)中的有界集映为有界的等度连续集.为证明α(Q(B))<α(B), 任取C(J,E)中非相对紧的有界集B.对C(J,E)中的有界集B, 记D=B(J), 则可得D⊂E有界.再由引理9知，α(D)≤2α(B).对∀t∈J,u∈B, 由引理10中的条件可得：

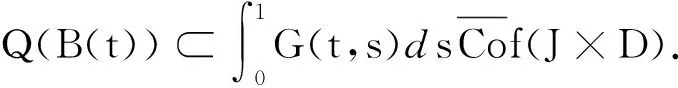
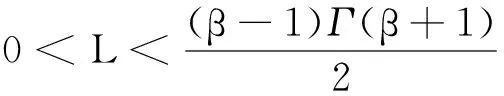
即Q:C(J,E)→C(J,E)为凝聚映射.类似于定理1的证明，用凝聚映射的Leray - Schauder不动点定理即可证明边值问题(2)解的存在性.

定理3设E为Banach空间,f:J×E→E连续.边值问题(2)至少存在一个解，若f满足定理1中的条件(H1)及如下条件(H4):

(H4) ∃0

下证Q:Ω0→Ω0为凝聚映射.任取Ω0中非相对紧的有界集B, 则B和Q(B)均是等度连续的.对于∀t∈J,u∈B, 由引理10及条件(H4)有：