分数阶中立型随机时滞微分方程的波形松弛方法

2022-09-13李佳敏丁小丽王苗苗

延边大学学报（自然科学版） 2022年2期

李佳敏，丁小丽，王苗苗

( 西安工程大学理学院，西安 710600 )

0 引言

分数阶中立型泛函微分方程由于可以模拟较为复杂的动力系统，因此受到学者们的重视．2014年，张艳敏[1]讨论了时间分数阶中立型时滞微分方程，并给出了该方程的数值解．2016年，杨水平[2]讨论了一类分数阶线性中立型延迟微分方程的初值问题，并给出了其解渐进稳定的充要条件．2017年，张玉峰等[3]研究了分数阶中立型时滞微分方程在Caputo导数意义下其解的存在唯一问题以及其通解表达式.2019年， Ding等[4]利用波形松弛方法给出了一类具有几乎扇形算子的分数阶随机演化方程的数值解．2021年，王子丰等[5]利用截断Euler - Maruyama法研究了中立型随机泛函微分方程的数值解.基于上述研究，本文研究一类分数阶中立型随机时滞微分方程的波形松弛方法，并给出了分数阶中立型随机时滞微分方程的波形松弛格式，以及该方法的收敛结果.

1 预备知识

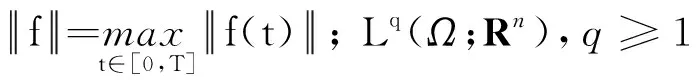
引理1[6]设0≤α≤1，φ(t)∈C(Ω;Rn)，则(T1,T2φ)(t)=(T2,T1φ)(t).

引理2[6]设0≤α≤1，φ(t)∈C(Ω;Rn)，且当i=1,2,3,…时以下关系成立:

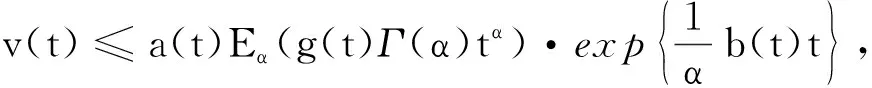
引理4[7]算子T1、 T2在空间C(Ω;Rn)上是紧算子，且σ(T1)=σ(T2)={0}，其中σ(·)为算子的谱.

考虑如下分数阶中立型随机时滞微分方程的初值问题：

(1)

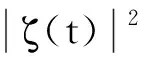
2 波形松弛方法的迭代格式及其收敛性分析

分数阶中立型随机时滞微分方程(1)的波形松弛方法为：

(2)

其中分裂函数F:Rn×Rn×Rn×Rn×[0,T]→Rn，G:Rn×Rn×Rn×Rn×[0,T]→Rn ×m，H:Rn×Rn×Rn×Rn×[0,T]→Rn满足：

F(x(t),x(t),x(t-τ),x(t-τ),t)=f(x(t),x(t-τ),t)，

G(x(t),x(t),x(t-τ),x(t-τ),t)=g(x(t),x(t-τ),t)，

H(x(t),x(t),x(t-τ),x(t-τ),t)=σ(x(t),x(t-τ),t)．

波形松弛方法的初始迭代函数满足x(0)(t)=ζ(t)，t∈[-τ,0]；x(0)(t)=ζ(0)，t∈[0,T]．

假设1假设M∈(0，1)，则对所有的φ，φ∈C([-τ,0];Rn)有 |D(φ)-D(φ)|≤M|φ-φ|.

假设2对任意的t∈[0,T]，x1,x2,x3,x4,y1,y2,y3,y4∈Rn，存在非负常数L1、L2和L3，并使得：

|F(x1,x2,x3,x4,t)-F(y1,y2,y3,y4,t)|≤

|G(x1,x2,x3,x4,t)-G(y1,y2,y3,y4,t)|≤

|H(x1,x2,x3,x4,t)-H(y1,y2,y3,y4,t)|≤

定理1设0≤α≤1，如果分裂函数F、G和H满足假设2，则在均方意义下由波形松弛方法(2)产生的序列({xk(t)}-τ ≤t ≤T，k=0,1,…)一致收敛于方程(1)的解{x(t)}-τ ≤t ≤T．

证明为了证明方便，定义：

F(t)=F(x(t),x(t),x(t-τ),x(t-τ),t),

G(t)=G(x(t),x(t),x(t-τ),x(t-τ),t)，

H(t)=H(x(t),x(t),x(t-τ),x(t-τ),t),

Fk(t)=F(xk +1(t),xk(t),xk +1(t-τ),xk(t-τ),t)，

Gk(t)=G(xk +1(t),xk(t),xk +1(t-τ),xk(t-τ),t),

Hk(t)=H(xk +1(t),xk(t),xk +1(t-τ),xk(t-τ),t).

根据以上定义，方程(1)和(2)可被写为：

(3)

(4)

当t∈[0,τ]时，将式(4)减去式(3)，且令ek(t)=xk(t)-x(t)，则可得：

(5)

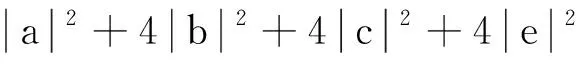
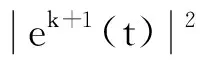
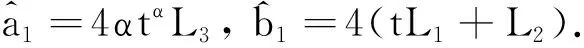
再根据算子T1、 T2的定义和可交换性以及引理3得：

(6)

由于

因此

(7)

根据算子T1、 T2的可交换性,将式(7)带入式(6)可得：

由文献[7]中的性质2.2知,算子T1、 T2对φ(t)∈C(Ω;Rn)是非递减的.对k进行数学归纳可得：

(8)

由引理1知算子T1、 T2可交换.再由引理4可知T1、 T2是定义在C(Ω,Rn)上的紧算子，且σ(T1)=σ(T2)={0}，因此{xk +1(t)}在区间[0,τ]上均方一致收敛，即

(9)

当t∈[τ,2τ]时，由式(4)减去式(3)可得：

xk +1(t)-x(t)=xk +1(τ)-x(τ)+D(xk +1(t-τ))-D(x(t-τ))+D(xk +1(τ))-

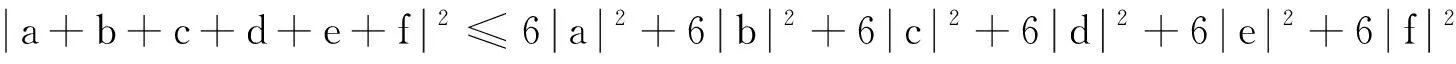
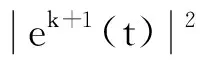
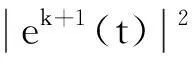
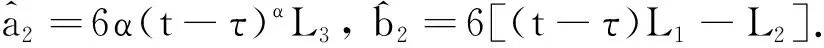
按上述归纳法处理算子T1和T2可得：

根据算子T1、 T2可交换及引理4知， T1、 T2是定义在C(Ω,Rn)上的紧算子，且σ(T1)=σ(T2)={0}.由此可知，{xk +1(t)}在区间[τ,2τ]上均方一致收敛，即

当t∈[nτ,(n+1)τ],n=0,1,…时，重复以上过程可得

定理1证毕.

3 数值模拟

由于难以求出分数阶中立型随机时滞微分方程的解析解，因此本文将分数阶中立型随机时滞微分方程的隐式Euler - Maruyama数值解作为真解.设0<α≤1, 并考虑如下形式的初值问题：

(10)

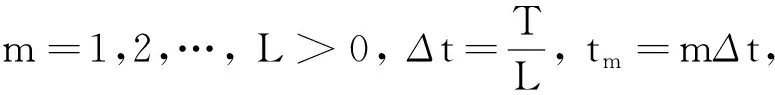
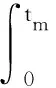
I1+I2+I3+I4+I5+I6+I7+I8.

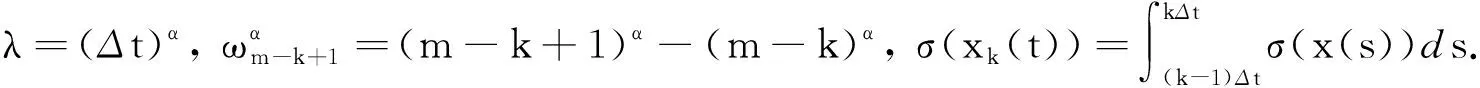
由此可得方程(10)的数值解为：

xm=xm -1+D(xm)-D(xm -1)+f(xm -1)Δt+g(xm -1)(B(tm)-B(tm -1))+

例1考虑如下分数阶中立型随机时滞微分方程的初值问题：

(11)

首先用波形松弛方法和Euler - Maruyama方法得出式(11)的解，然后将波形松弛解与真解进行比较和分析.用Matlab软件(取α=0.7,T=1,M=210)模拟出的式(11)的波形松弛解如图1所示，用Mathab软件模拟出的式(11)的波形松弛解和真解之间的误差如图2所示．由图1和图2可以看出，用波形松弛方法求解分数阶中立型随机时滞微分方程是有效的，且波形松弛方法在均方意义上是收敛的.