试论二次型化标准形的方法

2022-09-13王馨禹

数学学习与研究 2022年22期

◎王馨禹

(吉林师范大学，吉林长春 130012)

一、引言

我们通常借助二次型研究其对应二次曲线的性质.通过对二次型的学习，我们认识到，二次型中有一种特殊的形式，这种形式的二次型只有平方项，即二次型的标准形.二次型的标准形具有许多优良的性质，研究起来非常方便，并且由所学的知识我们知道，任何一种二次型都可以化成标准形，所以，我们在研究二次型时总是将二次型转化为标准形来解决问题.

通过进一步的学习我们了解到，化二次型为标准形是高等代数这门课程的重点之一，也是难点之一，更是困惑大学生的一大难题，而且二次型在与数学有关的其他领域也有着非常重要的应用，借助二次型，很多的数学问题将会得到很好的解答，因此，掌握化二次型为标准形的方法对于当代大学生来说十分重要，总结并研究化二次型为标准形的方法也非常有意义.

二、概念界定

1.二次型理论来源于解析几何中化二次曲线和二次曲面方程为标准方程的问题，对二次型理论的研究始于18世纪.直至今日，二次型的研究一直在进行着，人们对二次型理论的研究有近三百年之久，之所以研究二次型，是因为二次型对于我们研究一些数学问题仍然有着关键的作用，在其他领域也有非常重要的应用，有关二次型的相关理论仍然需要后人来继续探索.

设是一数域，一个系数在数域中的,,…,的二次齐次多项式

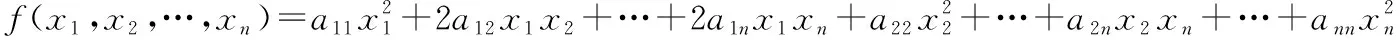
为数域上的一个元二次型.

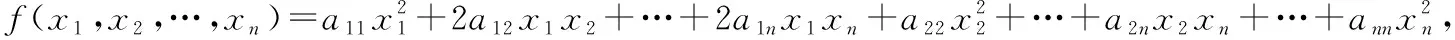
又由定理可知数域上的任意一个二次型都可经过非线性替换化成平方和形式，并且我们把二次型(,,…,)经过非退化线性替换所变成的平方和称为(,,…,)的一个标准形，也就是说任意一个二次型都有其标准形.因此掌握化二次型为标准形的方法十分重要.

三、二次型化标准形的方法

雅可比方法：

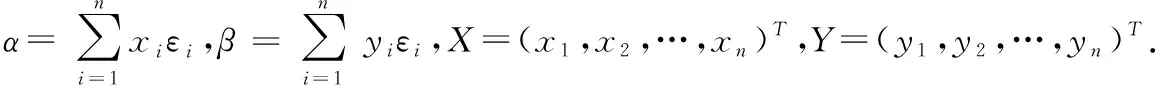
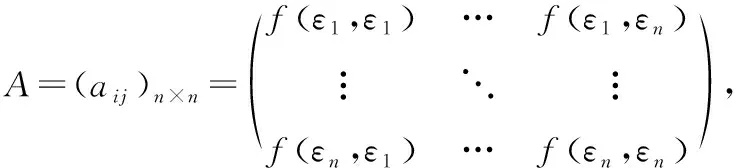
反之也同样成立.这说明在一组固定的基底下，通过矩阵二次型和对称双线性函数(,)=是可以互相唯一确定的.

再设,…,是的另外一组基底，然后令=()×是(,)关于这组基底的度量矩阵，又设=()×是由基,…,到基,…,的过渡矩阵，那么有=，也就是说一个对称双线性函数关于的两组基底的两个矩阵是合同的.

(,)==+…+，

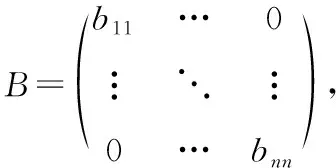
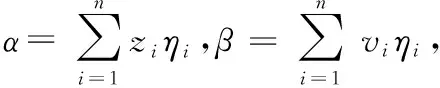
我们先从基,…,出发，讨论是否能构造基,…,：

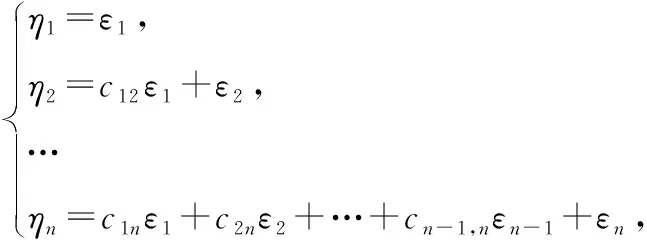
使得,=0，≠

显然可以用施密特法来构造正交基,…,：首先有

=(,)=(,)==Δ；=(,)=(+,)=(,)+(,)，

=(,)=(,+)

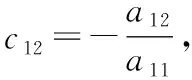
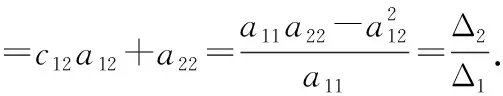
按照此方法一直做下去，我们能够得到,=1,…,由于=(,)=(,)=0，<，所以能够得到线性方程组：

=(,)=(,)

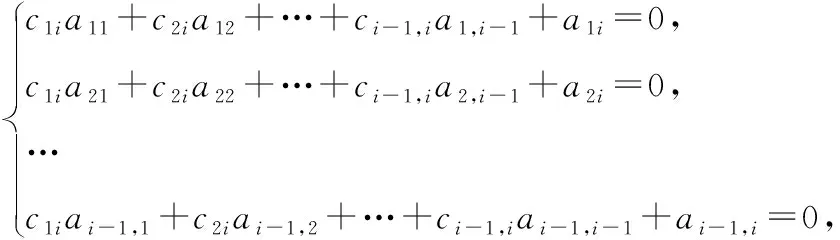
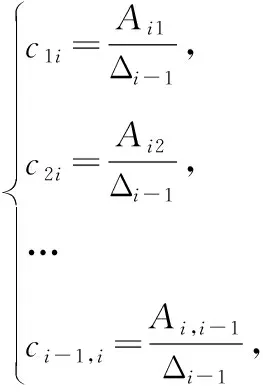
=(,1+2+…+-1,-1+)

=11+22+…+-1,,-1+

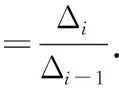
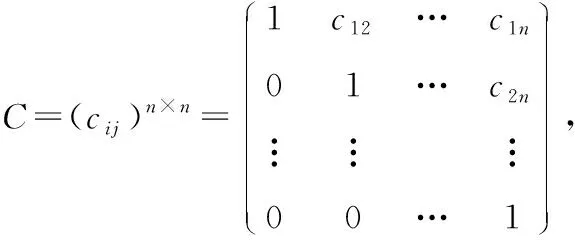
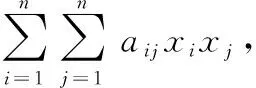
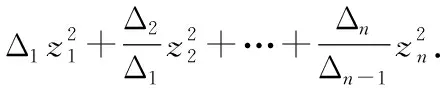
1用雅可比法将下面给出的二次型化为标准形，并写出所用的非退化线性替换.

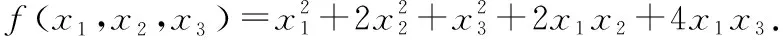
根据已知可以写出该二次型的矩阵

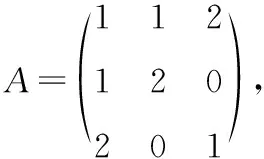
判断其顺序主子式Δ=1，Δ=1，Δ=-7都不等于零，故可以用雅可比方法.

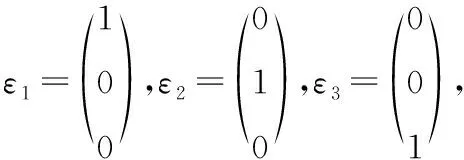
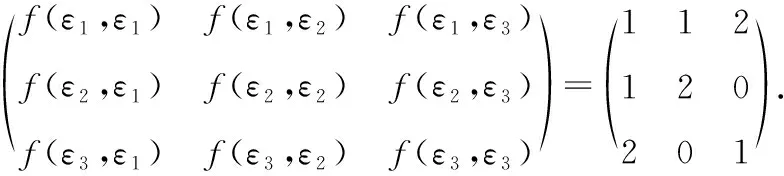
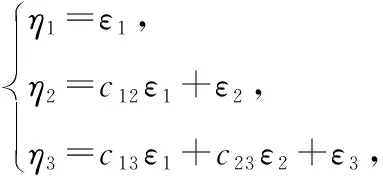
则有=,=,+=(,)+(,)=+1=0，

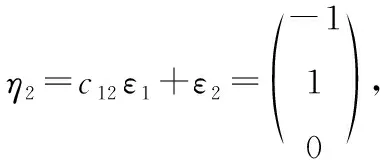
又由方程组

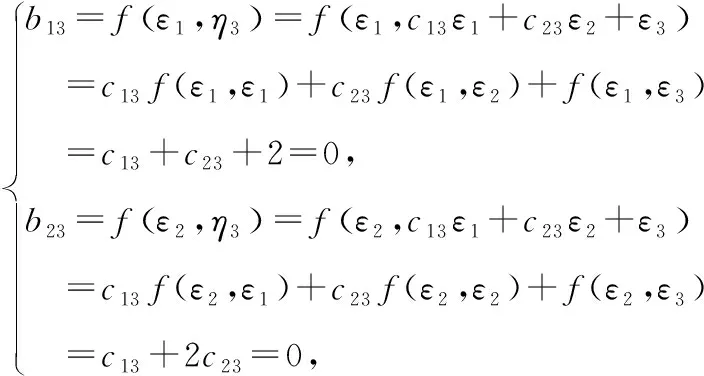
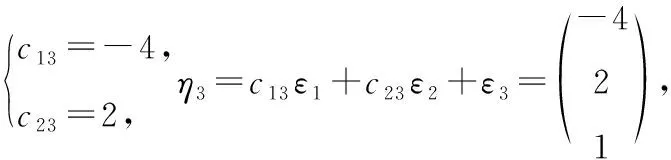
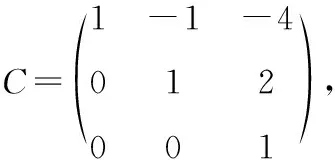
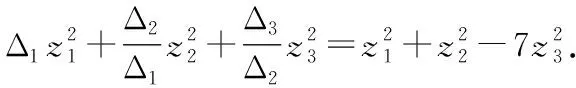
2将下面给出的二次型转化为标准形，并写出所用的非退化线性替换.

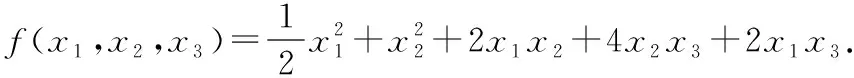
根据已知可以写出该二次型的矩阵

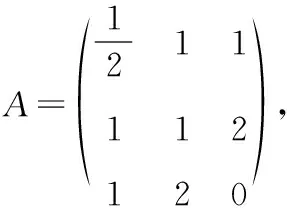
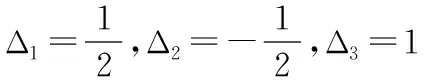
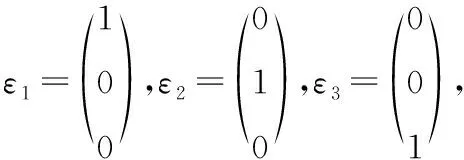
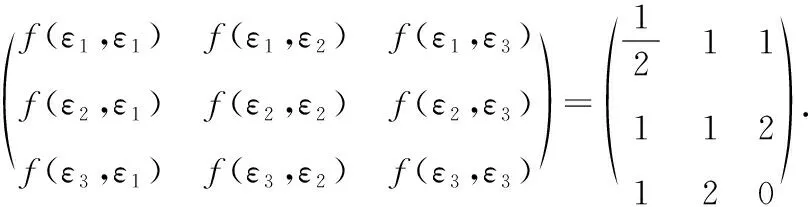
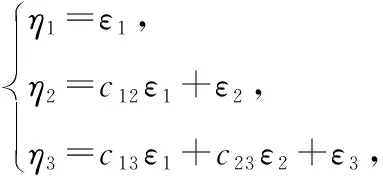
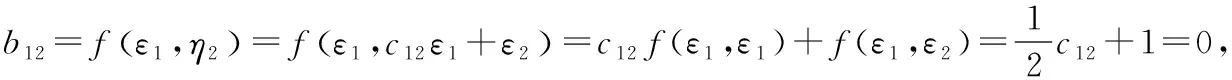
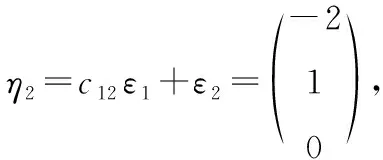
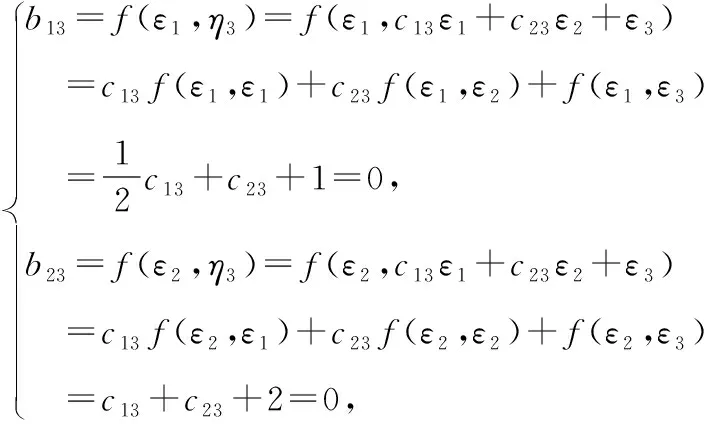
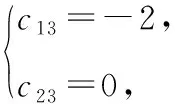
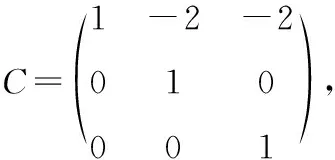
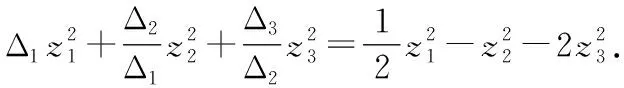
雅可比方法是借助对称双线性函数将二次型转化为标准形，虽然学生在学习高等代数时对双线性函数部分的内容掌握得不是特别熟练，但该方法理解起来比较容易.在用雅可比方法化二次型为标准形时，首先要判断元二次型的矩阵的前(-1)阶顺序主子式是否等于零，如果都不等于零，则可以用雅可比法.雅可比法是通过求矩阵的各阶顺序主子式来化二次型为标准形，可以比较快速直接地写出二次型的标准形，并且计算起来比较简单，在求线性替换的过程中不涉及矩阵的变换，也不涉及求矩阵的特征值和特征向量，只是求解方程及方程组，是一种比较好的化二次型为标准形的方法.