冠图PnoCm的两种度结合重构数

石黄萍,袁邓彬,张芬

(上饶师范学院 数学与计算机科学学院，江西 上饶 334001)

1 相关知识

在20世纪中叶，图的重构猜想是由Ulam在文献[1]和Kelly在文献[2]中提出并研究，它是指每个至少有3个顶点的图都能被它的主子图集所唯一确定，主子图集是指所有主子图组成的集合，而在图G中删除一个顶点v后得到的子图称为主子图，记为G-v。之后，许多学者对图的重构问题引起关注并对其加以研究。在1985年，Plantholt和Harary在文献[3]中引进了重构数的概念，它是指能够唯一确定图G的所需的主子图的最少数目。在2000年，Ramachandran在文献[4]中考虑在重构的主子图中增加了删除点的度信息(称为度结合主子图，即是指由主子图和删除点的度组成，记为(G-v,d(v))，这里，d(v)表示图G中顶点v的度)，并提出了度结合重构数的概念，即能重构图G的所需的度结合主子图的最少数目，记为drn(G)。在2012年，Monikandan等人在文献[5]中介绍了一致度结合重构数，是指任意k个度结合主子图都能重构图G的最小整数k，记为adrn(G)。本文继续对度结合重构数进行研究，主要确定PnoCm的度结合重构数和一致度结合重构数。

关于图的重构问题，很多学者已经总结了一些重要的结论。在2010年，Barrus和West在文献[6]中确定了k-正则图的度结合重构数的上界为min{k+2,n-k-1}，点传递图的度结合重构数的下界为3以及毛毛虫的度结合重构数为2。在2012年，Monikandan等人在文献[5]确定了完全图、轮图、圈、星图、完全二部图的一致度结合重构数。在2015年，石黄萍等人在文献[7]中确定了完全多部图和它的补图以及双帚图的两种度结合重构数。在2016年，马美杰等人在文献[8]中对类星图进行研究并确定了该图的两种度结合重构数。本文是在这些已有结论的基础上深入研究一类冠图的两种度结合重构数。

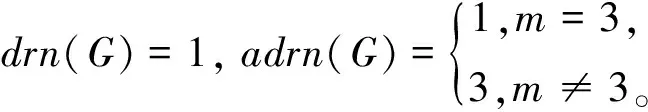
故只需确定当n≥2时，冠图PnoCm的两种度结合重构数。

2 主要结果

引理2.1令G=PnoCm(n≠2且m≠3)，则图G的1个度结合路点主子图和1个度结合圈点主子图可重构图G。

证明：假设这2个度结合主子图分别为(G-uk,d(uk))和(G-vl,3)。当d(uk)=m+1时，G-uk=Cm∪(Pn-1oCm)；当d(uk)=m+2时，G-uk=Cm∪(Pn1oCm)∪(Pn2oCm)，其中n1+n2=n-1。令图H表示在路点主子图G-uk中添加1个度为d(uk)的新点v'得到的且不同构于图G的重构图。由圈点主子图G-vl是连通图可知重构图H为连通图，故新点v'的邻点必落在路点主子图的每个连通分支中。

断言：新点v'与路点主子图G-uk中的圈分支Cm中的每个点均相邻。

(反证法)假设圈分支Cm中至少存在1个点与v'不相邻，则当d(v')=m+1时；图H中至少存在1个2-度点且v'至少有2个邻点落在另一连通分支的路点或圈点中，当d(v')=m+2时，图H中至少存在1个2-度点且v'至少有3个邻点分别落在另两个连通分支的路点或圈点中，故从图H中删除一个3-度点至多有n-2个割边，但已知的圈主子图中存在n-1个割边，矛盾，故假设不成立。

由v'在路点主子图G-uk的除Cm外其他连通分支中均只有一个邻点，若其中一个邻点为m+2-度点v''，则n≥4且Δ(H)=m+3,但因为Δ(G-vl)=m+2，所以在图H中删除的3-度点必与v''相邻，删除后的主子图中v''的度为m+2且有3个邻点的度数大于3，但已知的圈点主子图中m+2-度点均只有2个邻点的度数大于3，矛盾；若其中一个邻点为3-度点v''，则当n≠2且m≠3时，重构图H存在n+1个顶点的度大于3，若删除的3-度点是v''的邻点时，则得到的主子图只有1个2-度点，与已知的圈点主子图G-vl恰有2个2-度点矛盾；若删除的3-度点不是v''的邻点时，则得到的主子图仍存在n+1个顶点的度大于3，与已知的圈点主子图G-vl只有n个顶点的度大于3，故假设不成立。

由以上分析可知，重构图H的度结合主子图集中不包含度结合圈点主子图(G-vl,3)，故引理得证。

引理2.2令G=PnoCm，则图G的2个不同的度结合圈点主子图可重构图G，3个相同的度结合圈点主子图可重构图G。

证明：假设这2个不同的度结合圈点主子图分别为(G-vi,3)和(G-vj,3)，其中删除点vi和vj分别位于圈点类Vi和Vj中；这3个相同的度结合圈点主子图均为(G-vi,3)，其中删除点vi位于圈点类Vi中。令图H表示在圈点主子图G-vi中添加1个新点3-度点v'后得到的不同构于图G的重构图。记图G中与vi相邻且落在路Pn上的点为ui。

断言:新点v'至多有1个邻点落在圈主子图G-vi的路Pn上。

(反证法)假设v'至少有2个邻点落在圈点主子图的路Pn上，则从图H中删除异于v'的3-度点后至多只有n-2条割边，但已知的圈点主子图中含有n-1条割边，矛盾，故假设不成立。

若新点v'有1个邻点与G-vi的路Pn上的uk相邻，其他的2个邻点{va,vb}落在圈Cm上，下面分2种情形讨论va和vb的位置。

情形1 |N(v')∩N(uk)|=2

由此可知，N(v')∩N(uk)={va,vb}，当va，vb分别为G-vi中的2-度点和3-度点，此时ui和uk是同一点，则图H与G至多有2个相同的(G-vi,3)；当va，vb均为G-vi中有公共邻点的3-度点时，则图H与G有2个相同的(G-vi,3)；当va，vb均为G-vi中无公共邻点的3-度点时，则图H中增加2个4-度点，从中删除异于v'的3-度点比已知的圈主子图至少增加1个4-度点，故情形1不成立。

情形2 |N(v')∩N(uk)|≤1

从重构图H删除异于v'的3-度点后至多只有n-2条割边，但已知的圈主子图含有n-1条割边，故情形2不成立。

若v'的3个邻点全落在G-vi的圈Cm上，则当落在不同的圈上时，从图H中删除异于v'的3-度点的主子图至多只有n-2条割边，但已知的圈主子图含有n-1条割边；当落在同一圈上时，若该圈原为vi点所在的圈，则删除异于v'的3-度点后的主子图比已知的圈主子图中的m+1-度点相差1个；若该圈不为vi点所在的圈，则删除3-度点后的图比已知的圈主子图中的4+-度点至少增加1个，故此情况不成立。

由以上分析，引理得证。

引理2.3令G=PnoCm(m≥4)，若n∈{3,4}，则图G的3个度结合路点主子图可重构图G；若n≥5，则图G的4个度结合路点主子图可重构图G。

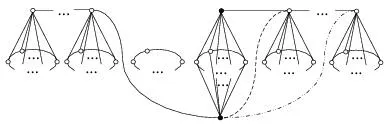
此时，圈分支Cm中至少存在1个点与v'不相邻，故在图H中删除1个异于v'的m+1-度或m+2-度点后得到的主子图比已知的另一路点主子图多1个2-度点。

断言2：新点v'的另2个邻点分别是主子图G-uk的2个冠图分支中的m+1-度点，假设断言不成立，分以下两种情形讨论：

情形2.2 新点v'的另2个邻点{ua,ub}分别落在主子图G-uk的2个冠图分支中，当ua,ub均是m+2-度点时，则从图H删除异于v'的m+2-度点得到的主子图的割边数至少比已知的路点主子图少1；当ua,ub中其中1个是m+2-度点时，不妨假设是ua且在冠图分支Pn1oCm中，此时，n1≥3且图H存在1个m+3-度点，由已知的另一路点主子图中无m+3-度点可知，欲得到已知的另一路点主子图，则删除的点与ua相邻，则图H与G至多有3个相同的路点主子图；当ua,ub至少有1个为3-度点时，则在图H删除异于v'的m+1-度或m+2-度点后得到的主子图中连通分支数比已知的路点主子图至少多1个或者不存在圈分支。故情形2.2不成立。

综上分析，引理得证。

证明：当n=1时，由定理1可知，drn(G)=1。当n=2且m=3时，图G的度结合主子图集里存在3个相同的度结合圈点主子图，由引理2.2可知，drn(G)=3。除此之外，图G的度结合主子图集里存在1个度结合路点主子图和1个度结合圈点主子图，由引理2.1可知，drn(G)=2。

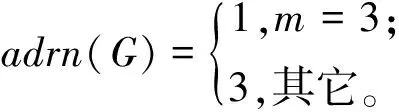
当n∈{2,3,4}时，由图2与图G有2个公共的度结合主子图(G-u1,m+1)可知，adrn(G)≥3。当n≥5时，由图3与图G有3个公共的度结合主子图(2个(G-u1,m+1)和1个(G-uk(≠1),m+2))可知，adrn(G)≥4。

图2 与图G有2个公共的度结合主子图

图3 与图G有3个公共的度结合主子图

下面证明确定值的上界。

当n∈{3,4}时，由引理2.1，2.2，2.3可知，图G的任意3个度结合主子图可重构图G，故adrn(G)≤3。

当n≥5时，由引理2.1，2.2，2.3可知，图G的任意4个度结合主子图可重构图G，故adrn(G)≤4。

当n=2时，要证图G的任意3个度结合主子图可重构图G，由引理2.1和2.2可知，只需证当m=3时，图G的1个(G-u1,4)和2个(G-v1,3)或者2个(G-u1,4)和1个(G-v1,3)可以重构图G。令图H表示在路点主子图G-u1中添加1个4-度点v'后得到的不同构于图G的重构图，由已知的圈点主子图G-v1可知重构图H是连通图，故新点v'的邻点落在G-u1的所有分支中，当v'的1个邻点落在圈分支C3中，则图H至多只有1个(G-u1,4)和1个(G-v1,3)；当v'的2个邻点落在圈分支C3中，则图H至多只有1个(G-u1,4)，所以adrn(G)≤3。