基于改进布谷鸟算法的水下多平台阵位优化
2022-09-09李鹏飞罗恒光王志欣唐立赫
李鹏飞,罗恒光,王志欣,唐立赫
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
海洋作为我国经济可持续发展的战略空间和国家安全不可或缺的保障,其信息技术的发展极大地提升了海洋权益的维护能力。水下无人平台凭借强机动性、适应性优势逐渐成为水下各种探测设备的搭载平台。平台及集群极大地拓展了作战能力,被视为“力量倍增器”[1]。
为了确保水下多基地信息探测体系的高效运转、水下空间态势信息的快速获取,保证多基地探测系统对任务区域的监测质量,Pompili等[2]提出了面向三维海洋空间覆盖部署问题的bottom-grid算法,即在海底三角网格节点部署的基础上调节节点深度。Wu等[3]为了实现水下三维空间的覆盖范围最大化,提出了一种基于Voronoi图的节点深度调节策略。蒋鹏等[4]考虑到水域中存在的障碍物与边界,提出了一种果蝇启发的水下传感器网部署算法,该算法以网络重连通为约束条件,将果蝇群的觅食行为与欧琼鸟飞行机制相结合,来求解节点移动位置和保持网络拓扑的相对稳定性,最后运用障碍物局部感知移动模型来避障,该算法在躲避障碍物的同时提高了网络覆盖率和连通性,减少了网络能耗。张颖等[5]提出了一种基于人工势场的分布式水下传感器网络部署优化算法,算法假设区域中存在的覆盖漏洞会产生对移动节点引力场,利用移动节点在人工势场法下所受虚拟力量化来指导节点移动,进而提高网络有效覆盖率,提升网络服务质量。文献[6]根据被动声纳的概率感知模型,兼顾水下环境影响,提出了基于模糊感知模型和模糊融合模型的水下传感器网络节点部署策略来解决网络二维覆盖问题。文献[7]提出了基于信度势场的算法解决三维部署问题,基于D-S证据理论定义了检测信度和信度覆盖,对水下传感器网络监测区域中信度覆盖的变化做了研究,结合目标在区域中分布的先验概率信息和被动声纳的探测概率模型,提出了节点部署算法。该算法建立了目标信度值信息与虚拟势场中受力的联系,依据感知节点的受力值来调节节点位置。鉴于水下环境复杂性及水下节点的成本高昂,由水下无人平台构成的探测网络不可能采用无线传感器网络大规模随机部署的方案[8]。所以,如何用尽量少的节点实现目标区域有效覆盖的最大化是国内外的研究侧重点。早期关于水下探测网络的研究大多基于通用且简化的数学模型,对水下环境的涉及很少。本文基于水下平台信息流程及平台能力,量化地给出了多种因素联合约束下的水下多平台探测效能;选定优化算法中的布谷鸟算法(Cuckoo Search Algorithm,CSA),引入高斯变异算子、模拟退火机制、更新淘汰率来改进优化算法的效率与精度,用改进算法对区域内多平台阵位进行了优化。
1 协同探测效能
多基地系统是以双基地系统为基本单元混合而成的网络形式,其立体模型如图1所示。
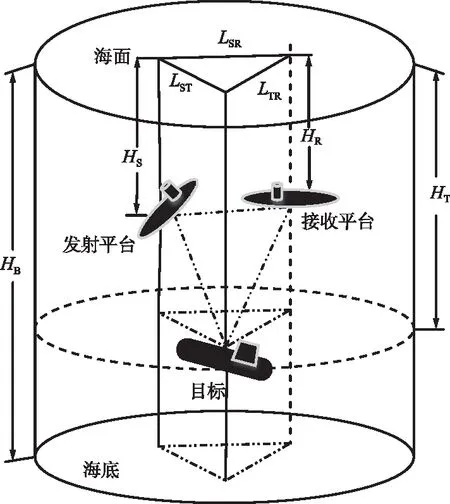
图1 双基地系统探测立体模型Fig.1 Detection stereo model of bistatic system
图1中,HS为发射台深度,HT为目标深度,HR为接收台深度,HB为海深,LST为发射平台与目标的水平间距,LTR为目标与接收平台的水平间距,LSR为发射与接收平台的水平间距。
根据图1,探测具体实现过程如下:
步骤1:确定系统工作频率、带宽、声源级、收发端指向性指数和深度等参数;
步骤2:输入海洋环境参数,生成海洋环境信息;
步骤3:目标信息输入,如目标深度等;
步骤4:计算信号从发射端到目标以及目标散射、反射到接收端的传播衰减;
步骤5:求取声线入射角与收发之间的分置角,结合目标强度模型计算目标强度;
步骤6:选择以环境噪声为背景的声纳方程计算海洋环境噪声;
步骤7:计算信噪比,结合信噪比与探测概率的关系得到探测概率。
探测概率取决于信噪比和检测阈[9],即:
Pd(X,Y)=e-DT/(1+SNR(X,Y)),
(1)
式中,信噪比由信号余量SE和检测阈DT相加得到。进行声纳设计,信号余量取值为0时,对应探测概率为0.5,虚警概率为10-4[10]。
以海洋环境噪声为主要干扰的双基地声纳方程为:
SL-TLST-TLTR+TS-NL+DI=DT,
(2)
式中,SL为声源级;TLST,TLTR为传播损失;TS为目标强度;NL为海洋环境噪声级;DI为接收指向性指数;DT为检测阈。
1.1 传播损失计算
扩展损失、吸收损失和散射构成了声波传播过程中主要的衰减。传播损失仅考虑波阵面扩展损失和介质声吸收损失,即:
TL=TL1+TL2。
(3)
由传播损失定义的球面波的传播损失为:
(4)
对于海水介质声吸收引起的传播损失计算方法如下:
TL2=r·a(dB),
(5)
式中,r为声波传播距离,单位km;α为海水声吸收系数,单位dB/km,具体表达式为:
(6)
式中,f为声信号频率,单位kHz。快速计算传播模型下,传播途中任意距离处的传播损失可以快速得出。
1.2 目标强度计算
目标强度(TS)是声纳主动信息流程中特有的参数,描述了水下目标对探测声波的反射能力。TS的表达式如下:
(7)
式中,Ir|r=1为入射声波相反方向上、离目标声中心1 m处的回波声强;Ii为目标处的入射声。文献[11]给出了水下目标高逼真金属模型下不同入射角和分置角组合下的目标强度,如表1所示。
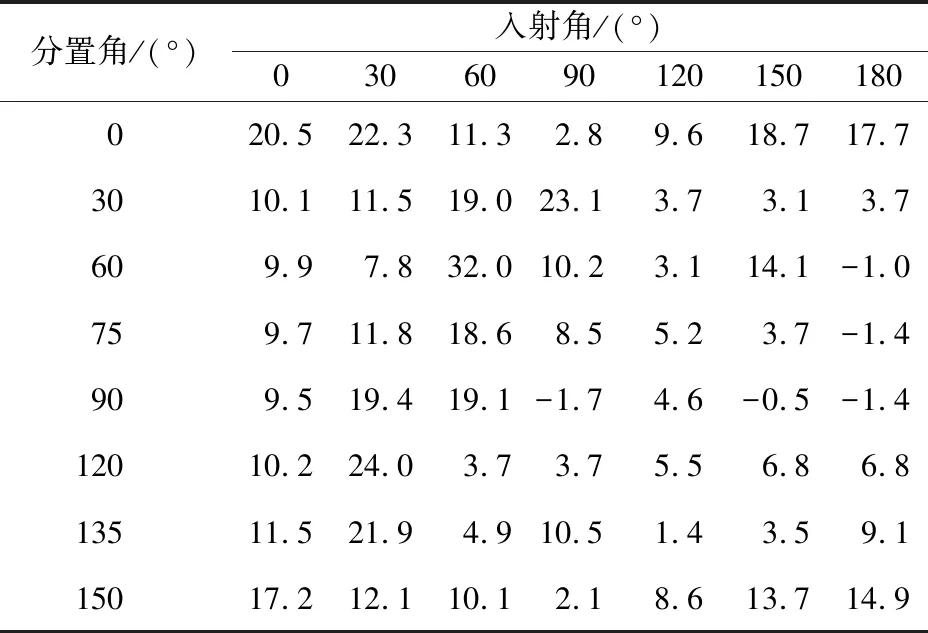
表1 不同入射角与分置角组合下的目标强度
1.3 环境噪声计算
1.3.1 风成噪声
APL-UW给出了风成噪声(10~1 000 kHz)频段合适的参数化模型[12]:
42.2+22.4lgv-15.9lgf-δ(ΔT),
(8)
(9)
式中,v为风速,且要求v≥1 m/s;f为噪声频率,单位kHz;ΔT为温度差,单位K;有:
ΔT=Tair-Twater。
(10)
Kuperman和Ferla根据测量结果并模仿APL模型,得到了400 Hz以下用于估计低频段风成噪声的公式[13]:
(11)
结合式(8)和式(11),得到2个模型之间的过渡噪声[14]:
41.2+22.4lgv-10lg(1.5+f1.59)-δ。
(12)
1.3.2 雨噪声
在APL模型中,20 kHz处的噪声谱级可以表示为:
(13)
式中,R为降雨量,单位mm/h;v为风速,单位m/s。风速v通过a和b来体现对噪声级的影响:
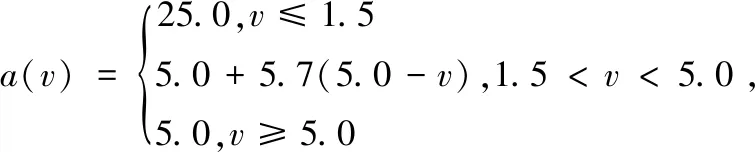
(14)
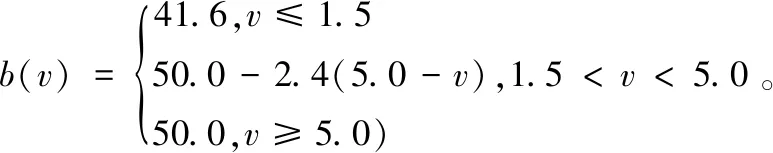
(15)
APL模型基于20 kHz频点处的雨噪声级在1~100 kHz频段的雨噪声谱级:
(16)
1.3.3 远处航船噪声
低频条件下的单极子声源个体的辐射声场都会与其在海面处反射的波相干涉,从而构成一个偶极子。所以将远处船群建模为一片偶极子的方法可行,得到偶极子的噪声级为:
(17)
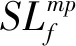
(18)
海洋环境总噪声是多种来源噪声的综合效果,通常通过“功率求和”的方式得到总的噪声级:
NL=10lg(10NLwind+10NLrain) 。
(19)
2 改进布谷鸟算法
2.1 基本布谷鸟算法
CSA因参数少、收敛快、全局搜索能力强、算法操作简单和易于实现被广泛地应用于多目标优化、工程设计、微电网优化以及计算机网络等领域[16]。
自然界中的布谷鸟用寄生的方式繁衍后代,将卵产在其他鸟巢中,由其他鸟来养育自己的下一代。一旦宿主鸟发现外来鸟蛋时,宿主鸟就会抛弃外来鸟蛋。Yang和Deb为了模拟布谷鸟在寻窝过程中的行为,设定以下3个理想状态:
① 布谷鸟一次产一个卵,随机选择鸟巢来孵化;
② 符合条件的被寄生鸟巢保留至下一代;
③ 寄生鸟巢数目固定,且鸟蛋被寄主发现的概率为Pc。
基于以上理想状态,鸟巢位置的更新公式为:
(20)
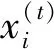
L(λ)~u=t-λ,1≤λ≤3。
(21)
算法具体流程如下:
步骤1:随机产生作为初始化种群的n个鸟巢位置;
步骤2:计算适应度,找出并保留最好的鸟巢位置;
步骤3:莱维飞行更新鸟巢位置;
步骤4:计算新位置的适应度,并同原鸟巢的适应度对比,择优保留;
步骤5:将Pc与代表外来鸟蛋被发现概率的随机数作比较,若Pc较大,则重新随机生成一个新鸟巢位置并计算适应度;
步骤6:若满足终止条件,输出最好的鸟巢位置,否则回到步骤3。
2.2 改进布谷鸟算法
CSA的寻优效率受限于莱维飞行的搜索策略,莱维搜索步长和方向的随机性很大,前期搜索快,后期收敛速度慢,求解精度低,易陷入局部最优[18]。为了提高算法求解效率和精度,本文引入高斯变异算子、更新淘汰率和模拟退火机制,对CSA进行改进。
高斯变异算子:在位置更新时加入变异操作,以较高概率在小邻域内产生一个正态分布的随机数对个体产生干扰形成变异。每个染色体个体解的目标变量为X,变异标准差为σ。染色体包含目标变量X和标准差σ两部分,形式如下:
X(t+1)=X(t)+N(0,σ)。
(22)
X和σ之间的关系为:
(23)
(24)
式中,系数β,γ是待定参数,β通常取1,γ取0;F(X(t))为当前个体的适应度;P(σ)为N(0,σ)的概率密度。
更新淘汰率:随着迭代次数的增加,算法计算的结果会在最优解附近摆动,不会精确收敛。利用梯度下降思想改进淘汰概率[19],其随迭代次数变化如下:
Pc=0.9iterationPc0,
(25)
式中,iteration为迭代次数;Pc0为初始淘汰概率。
模拟退火机制:将问题的求解过程转化为退火过程。控制参数T表示退火过程中的温度,T每取一个值,算法按Metropolis接受准则,往复进行“新解产生—判断—接受或舍弃”的循环而达到平衡。算法凭借不强求新解优于当前解的思想提升跳出局部极值的能力。
Metropolis接受准则如下:
(26)
式中,ΔE为前后状态系统能量差;P(ΔE)为接受新解的概率;k为常数;T为当前的绝对温度。
改进CSA详细流程如图2所示,步骤如下:
步骤1:随机产生作为初始化种群的n个鸟巢位置;
步骤2:计算适应度,找出并保留最好的鸟巢位置;
步骤3:莱维飞行更新鸟巢位置;
步骤4:高斯变异更新鸟巢位置;
步骤5:计算新位置的适应度,并同原鸟巢的适应度对比,若新解优于当前最优解,用新解作为当前最优解;若新解适应度较当前最优解的适应度差,按淘汰率和Metropolis接受准则决定新解的取舍;
步骤6:若满足终止条件,输出最好的鸟巢位置,否则回到步骤3。
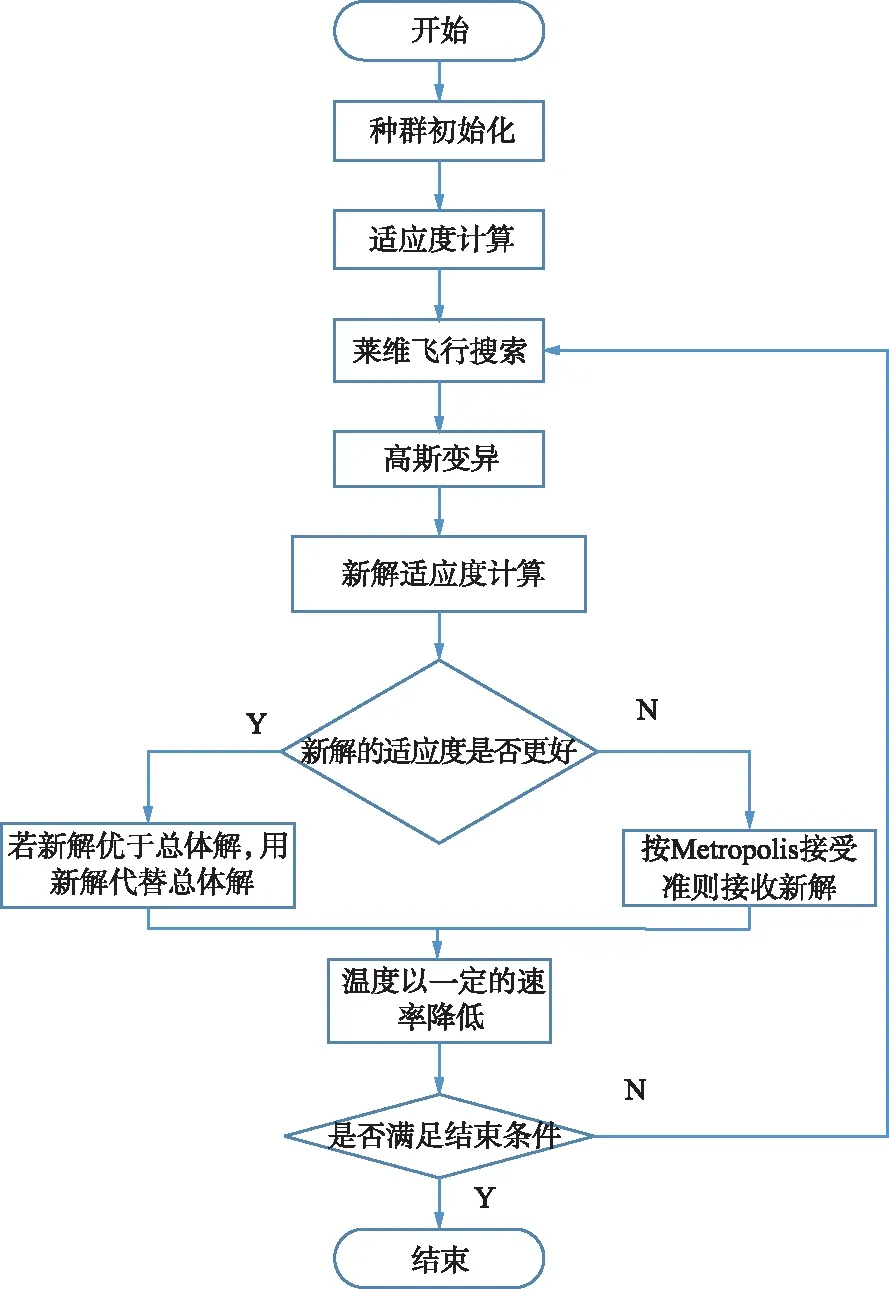
图2 改进布谷鸟算法流程Fig.2 Improved CSA flow
3 多平台阵位优化
水下监测网络任务区域覆盖质量直接关系到网络的整体效能,通过合理部署平台位置,用较少的平台数目达到较高的区域有效探测覆盖率,将覆盖盲区和重叠区降到最低。多种可供选择的装备平台构成的区域水下探测系统创生出新的优化配置原则。基本原则如下:
① 节点最少原则。给定任务区域,给定有效覆盖面积占比要求,优化平台位置,最大程度减少冗余平台。
② 区域有效覆盖面积最大原则。给定任务区域,给定平台数量,优化平台阵位使区域有效覆盖面积最大。
③ 探测概率最大原则。给定任务区域,布放平台监测到任意方向闯入的目标,使目标在该区域以任意航迹穿过时被发现的概率最大。
本文以平台的区域有效探测覆盖率为适应度值,通过改进CSA对多个平台的阵位信息进行优化来提高区域的探测覆盖率。
4 仿真结果及分析
实验设置种群数为10,每个种群含有的个体数目为平台数目的2倍,Pc0=0.25,初始温度为100 K,结束温度为0.01 K,温度衰减系数为0.99,迭代次数200。
海况信息:任务区域大小为22 km×22 km,区域步长0.1 km,区域平均声速1 450 m/s,海深4 500 m,海底底质为沙质,声速1 600 m/s,海平面上下温差5 K,海面风速5 m/s,降雨量2.5 mm/h,航运密度1.3 船/平方海里,假设目标各向同性且强度为16 dB,目标深度100 m,目标静止,航向0°。
发射平台、接收平台相关参数信息如表2所示。
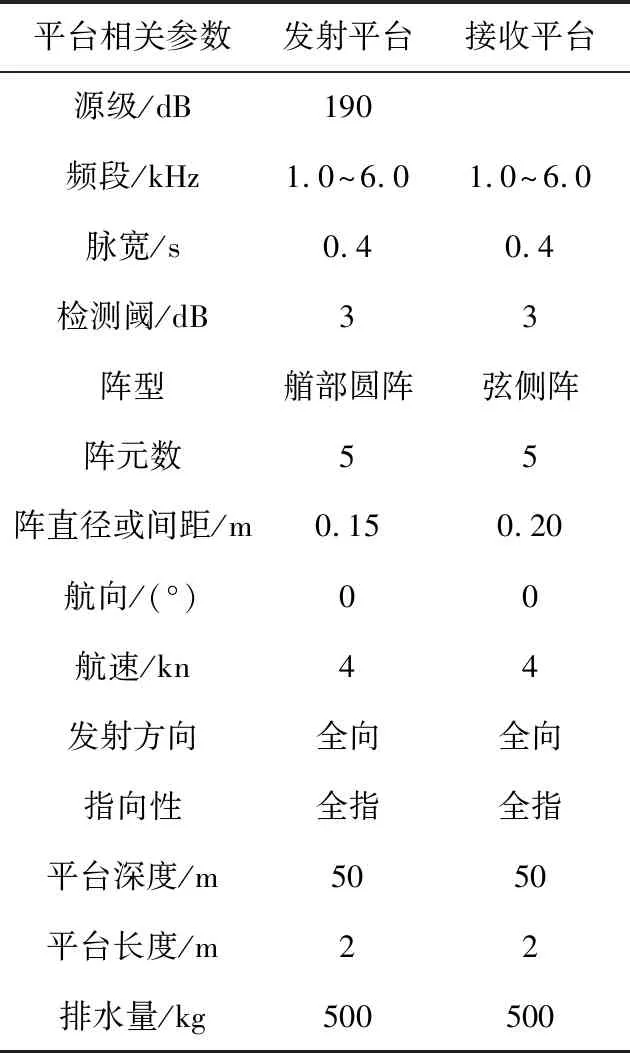
表2 平台工作参数
本文用改进CSA对1个发射平台和3个接收平台组合、1个发射平台和4个接收平台组合、2个发射平台和3个接收平台组合进行了阵位优化仿真,对应的优化后阵位示意图和对应的覆盖率进化曲线如图3~图8所示。
用改进CSA对阵位进行优化,由图4可以看出,一发三收工作模式下区域有效探测覆盖率由52%提高到63%,覆盖率在60次时达到收敛。由图6可以看出,一发四收工作模式下区域有效探测覆盖率由72%提高到84%,覆盖率在80次时达到收敛,两发三收工作模式下区域有效覆盖率由84%提高到98%,覆盖率在120次时达到收敛。由图3、图5和图7可以看出,改进CSA对一发多收、多发多收工作模式下的平台有很好的部署优化效果。
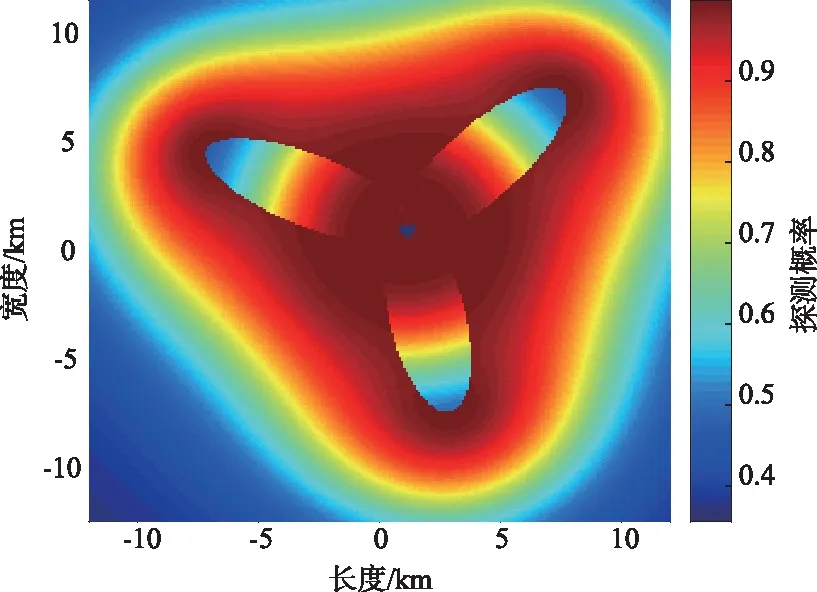
图3 一发三收模式下平台的优化阵位示意Fig.3 Schematic diagram of optimized array of platform in one-transmitter three-receiver mode
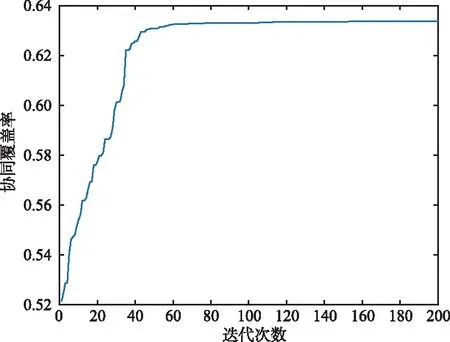
图4 一发三收模式下覆盖率进化曲线Fig.4 Evolution curve of coverage rate in one-transmitter three-receiver mode
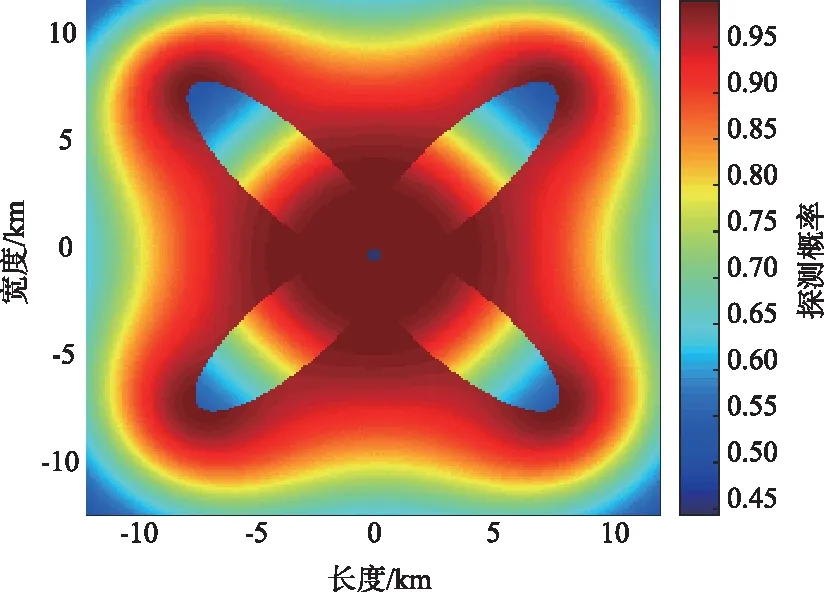
图5 一发四收模式下平台的优化阵位示意Fig.5 Schematic diagram of optimized array of platform in one-transmitter four-receiver mode
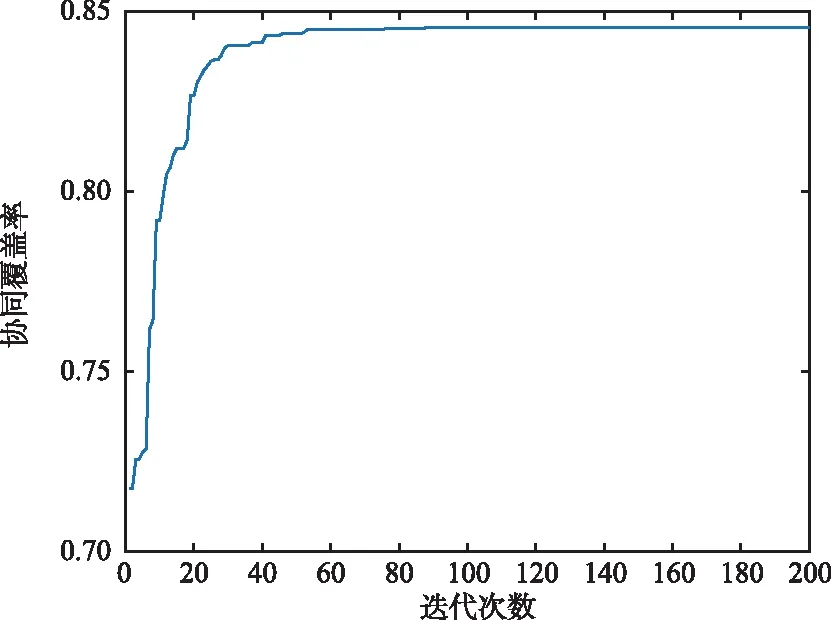
图6 一发四收模式下覆盖率进化曲线Fig.6 Evolution curve of coverage rate in one-transmitter four-receiver mode

图7 两发三收模式下平台的阵位优化Fig.7 Schematic diagram of optimized array of platform in two-transmitter three-receiver mode

图8 两发三收模式下覆盖率进化曲线Fig.8 Evolution curve of coverage rate in two-transmitter three-receiver mode
5 结束语
本文给出了水下无人平台协同探测效能模型,应用CSA优化平台阵位,使多个水下无人平台效能发挥最大化;针对CSA易陷入局部最优的问题,引入高斯变异算子、更新淘汰率和模拟退火机制,对CSA做了改进;对基于区域最大覆盖面积原则的多平台进行部署优化,用改进CSA对区域内一发多收、多发多收不同工作模式下的多平台阵位进行优化,区域有效探测覆盖率较随机部署显著提高。
考虑到工程应用及实际海洋环境的时变性,接下来将进一步研究实际海洋环境耦合作用下的平台探测效能,对算法继续优化,便于算法后续移植到具体的设备上。
