基于IIVSSLMS低轨卫星导航增强系统数字域自干扰对消算法研究
2022-09-09孟祥芳易卿武
孟祥芳,易卿武,谢 松,朱 研
(1.河北科技大学 信息科学与工程学院,河北 石家庄 050018;2.卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081)
0 引言
全球导航卫星系统(Global Navigation Satellite System,GNSS)[1]作为获取空间信息的重要基础设施,其定位精度只能达到米级,仅依靠GNSS很难满足自动驾驶和智慧农业等高精度领域的实用需求。
低轨卫星(Low Earth Orbit,LEO)的发展为解决上述问题提供了思路,低轨星座能够与中高轨GNSS星座形成互补,可以显著提高GNSS的精度、完好性、连续性和可用性[2],低轨导航增强(LEO-NA)技术已经成为卫星导航领域的关注热点,美国[3]、欧洲[4]和国内[5-6]多个机构对此展开了系统性的研究。实现该技术需要在低轨卫星上搭载导航增强载荷,来播发双频导航增强信号,增强信号频率一般选择L波段。但是,播发L频段导航增强信号会对低轨导航增强载荷正常接收信号产生干扰,这里称之为自干扰。因此,研究低轨导航增强载荷干扰对消技术以避免自干扰成为推动低轨高精度定位实际应用的关键。自干扰对消技术主要包括空域、模拟域和数字域自干扰对消技术。目前,学界已经对空域和模拟域自干扰对消技术进行了大量的研究[7-8],关于数字域自干扰对消的研究相对匮乏,而空域和模拟域并不能完全抑制干扰,剩余干扰需要在数字域中进一步消除。
数字域自干扰对消技术主要分为基于信道估计的干扰对消和自适应干扰对消2种,其中,基于信道估计的自干扰对消技术又分为基于导频信号的信道估计和基于自适应滤波算法的信道估计2种。文献[9-11]均采用基于导频信号进行信道估计的方式,这些方法存在带宽利用率低、时效性差的问题,为此,研究人员提出了一系列采用最小均方(Least Mean Square,LMS)[12]算法进行信道估计的干扰对消方案,LMS算法具有原理简单、计算复杂度低和易于实现等优点,成为应用最广泛的自适应滤波算法[13]。文献[14]提出了基于谱成型的自适应数字干扰对消方法,该算法基于传统的LMS算法,存在收敛速度与稳态误差相互制约的问题。文献[15]为了改善这一不足,提出了基于迭代变步长LMS的数字域自干扰对消算法,在保证稳态误差较小的情况下有效提高算法的收敛速度,但是该算法中步长因子临界值的选取需要发射信号的先验知识。文献[16]在文献[15]的基础上,提出了一种基于迭代变步长变换域的最小均方算法,但是依赖发射信号先验知识的问题依然存在。
基于LMS算法进行信道估计不需要占用额外的带宽,易于实现,但同时也存在收敛速度和稳态误差相互制约的问题。为了更好地平衡LMS算法收敛速度和稳态误差,近年来关于变步长LMS算法的研究被相继提出。在文献[17-18]提出的变步长LMS算法中,在算法的初始阶段令步长为较大值以提高收敛速度,在收敛时间附近采用较小的步长来减小稳态误差,但是这些算法容易受到相关噪声和其他因素的影响。文献[19]提出了一种基于Sigmoid函数的变步长LMS自适应滤波算法,该算法在步长参数和误差信号之间建立了非线性函数关系,并根据误差信号之间的相关性调整步长,使步长不受相关噪声的影响。文献[20]提出了一种新的变步长LMS自适应滤波算法,通过调整滤波系数和步长因子,保证加快收敛速度的同时减小了稳态误差。
综合考虑上述方案的优点和不足,本文提出了一种改进的迭代变步长最小均方(Improved Iterative Variable Step-size Least Mean Square,IIVSSLMS)数字域自干扰对消算法,并将其应用到低轨卫星导航增强系统中,用于解决导航增强信号和低轨导航增强载荷正常接收信号产生的自干扰问题。该算法通过在初始阶段将步长因子固定为较大值,提高了收敛速度,并利用当前误差信号和上一步误差信号的自相关估计共同调节步长因子,在降低突发脉冲干扰产生的不利影响的同时减小了稳态误差。仿真结果表明,该算法有较快的收敛速度和较大的干扰对消比。
1 数字域自干扰对消原理
数字域自干扰对消的原理框图如图1所示。
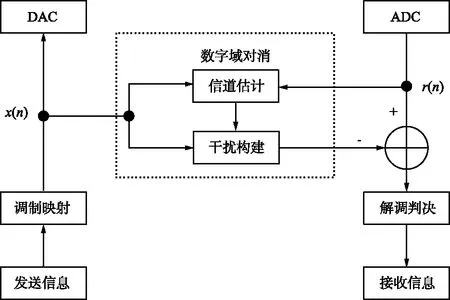
图1 数字域自干扰对消原理框图Fig.1 Schematic block diagram of digital-domain self-interference cancellation
采用LMS算法进行信道估计的数字域自干扰对消的基本思路为:首先采用LMS算法得到估计的自干扰信道冲激响应,然后自干扰信道冲激响应结合发射信号得到重构的自干扰信号,最后在接收信号中减去重构的自干扰信号,实现数字域自干扰对消。接收到的数字基带信号为:
r(n)=x1(n)+d(n)+ε(n)=
x(n)wM+d(n)+ε(n),
(1)
式中,x(n)为由发射信号构成的L×M维Toeplitz矩阵;wM表示M阶自干扰信道响应,为M×1维;x1(n)为模拟域干扰对消后剩余的L×1维自干扰信号向量;d(n)为正常接收的信号,即期望信号,ε(n)为加性噪声,二者均为L×1维;r(n)为模拟域干扰对消后的L×1维接收信号向量,接收信号由剩余的自干扰信号、正常接收信号和噪声组成。
干扰对消后得到的误差信号,即LMS算法的反馈误差,由接收信号和估计的自干扰信号之间的差值表示,误差信号为:
(2)
LMS算法滤波系数的更新公式为:
(3)
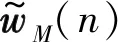
2 基于IIVSSLMS的数字域自干扰对消
本节主要对IIVSSLMS算法进行详细描述。采用IIVSSLMS算法能够在数字域解决低轨卫星导航增强系统中导航增强信号对低轨导航增强载荷正常接收信号产生的自干扰问题。该算法通过对自干扰信道进行估计得到自干扰信道冲激响应,然后结合发射信号得到重构的自干扰信号,最后将重构的自干扰信号从接收信号中减去来实现干扰对消。在算法的初始阶段(本文取200,迭代次数n为2 000),将步长因子固定为较大值(本文在参数(1)的条件下取0.8,在参数(2)的条件下取0.75),用来提高收敛速度,当迭代次数超过200时,采用迭代次数和当前误差信号与上一步误差信号的自相关估计共同调节步长因子,使步长因子维持在一个较小的范围内,从而在消除不相关噪声向量对收敛性能不利影响的同时减小系统的稳态误差。本文通过对箕舌线函数[21]变形,得到步长因子:
(4)
式中,a和β为常数,当a和β发生变化时,μ(n)和e(n)的关系分别如图2和图3所示。由图2可知,a越大,误差在接近于0时变化越剧烈,从而导致步长发生突变,影响系统稳态性能,所以a的取值不应过大,同理β也需要合理选择。
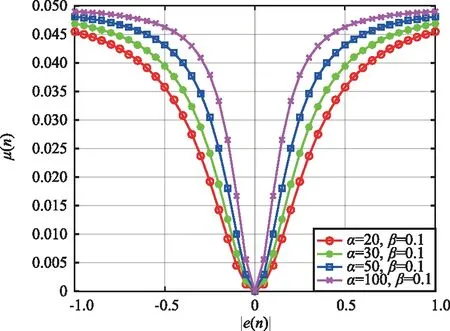
图2 参数a的取值对步长因子的影响Fig.2 Effect of parameter a value on step factor
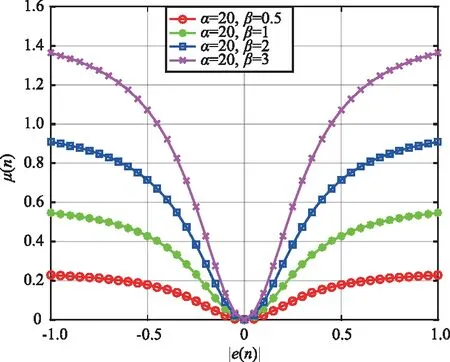
图3 参数β的取值对步长因子的影响Fig.3 Effect of parameter β value on step factor
在初始阶段,取较大的步长因子使收敛速度提高的同时也会造成系统的稳态误差增大,为了改善这一不足,对权重进行归一化处理,得到权重更新的表达式,即估计的自干扰信道冲激响应为:
(5)
式中,η是个非常小的整数,用于解决当x(n)太小时存在最小值的问题。由式(5)可知,估计的自干扰信道冲激响应由步长因子、发射信号以及误差信号共同控制。
根据第2部分的数字域自干扰对消原理,给出了IIVSSLMS算法流程,如图4所示。
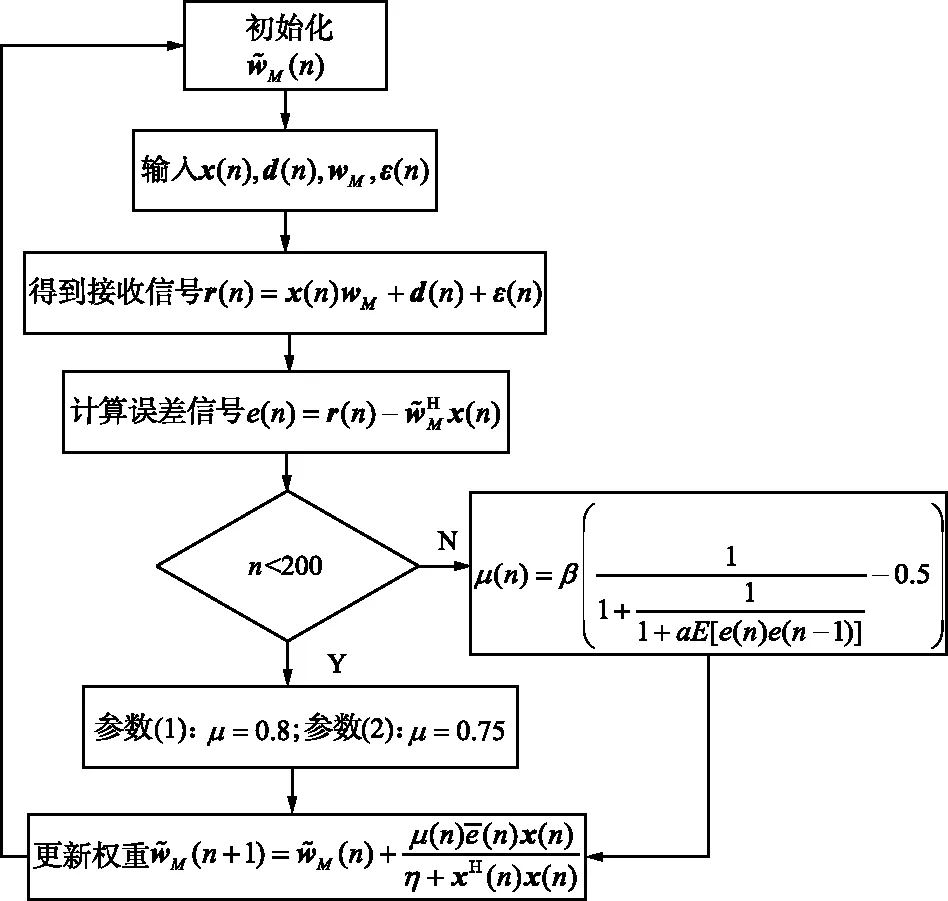
图4 IIVSSLMS算法流程Fig.4 IIVSSLMS algorithm flow chart
基于IIVSSLMS数字域自干扰对消算法的详细步骤为:
步骤1设置IIVSSLMS算法的信道阶数M,并保证M不小于自干扰信道等效阶数M′,根据低轨卫星导航增强系统中的参数确定a和β的最佳取值;
步骤3执行式(2),计算反馈误差e(n);
步骤4步长迭代:
如果n<200,μ在参数(1)的条件下取0.8,在参数(2)的条件下取0.75,否则执行式(4);
步骤5执行式(5),更新估计的自干扰信道冲激响应。
3 性能分析
主要从理论层面分析基于IIVSSLMS低轨卫星导航增强系统中数字域自干扰对消算法的性能,并推导IIVSSLMS算法的收敛因子和稳态条件下干扰对消比(Interference Cancellation Ratio,ICR)的表达式。
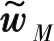
根据接收的自干扰信号是发送信号通过信道wM得到的,因此得到误差信号为:
(6)
式中,y(n)=d(n)+ε(n),其均方误差为δ2。
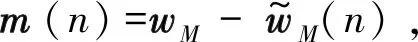
e(n)=mH(n)x(n)+y(n),
(7)
E{|e(n)|2}=E{|mH(n)x(n)+y(n)|2}=
E{mH(n)x(n)xH(n)m(n)}+δ2=
E{mH(n)Rm(n)}+δ2,
(8)
式中,R=E{x(n)xH(n)}是x(n)的统计平均自相关矩阵,为共轭对称矩阵。
对R进行对角化,得到:
(9)
式中,U为酉矩阵;λj为R的特征值;Λ为对角矩阵。
再令M(n)=UHm(n),得到:
(10)
由于R=UΛUH,m(n)=UM(n),对式(8)化简得:
E{|e(n)|2}=E{MH(n)ΛM(n)}+δ2=
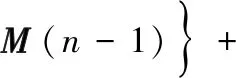
(11)
式中,tr(·)表示矩阵的迹,以此类推得到:
E{MH(0)ψ(n)M(0)}+
(tr[φ(0)+…+φ(n-1)]+1)×δ2,
(12)
式中,
(13)
由于酉矩阵不改变矩阵的迹,则对式(12)进行变形,得到:
E{|e(n)|2}=E{mH(0)ψ(n)m(0)}+
(14)
式中,
0≤j≤M-1,
(15)
0≤j≤M-1。
(16)
(17)
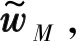
(18)
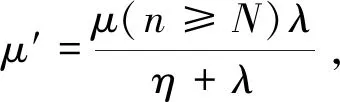
(19)
由于当n≥N时,μ′很小,所以有2-μ′≈2,对式(19)进行化简得到:
(20)
因为干扰对消比的定义为ICR=10lg(Pn前/Pn后),其中,Pn前和Pn后分别表示系统相消前输入的自干扰信号功率和系统相消后输出的剩余自干扰信号功率。设接收信号的功率为Pr=PI+δ2,则IIVSSLMS算法收敛状态下的干扰对消比为:
(21)
4 实验仿真与结果分析
为了评估本文提出的基于IIVSSLMS数字域自干扰对消算法的性能,采用Matlab进行仿真,并将本文算法与文献[15,19-20]中的变步长LMS算法在收敛速度和干扰对消比2个方面进行比较。ICR反映了系统对消性能,对于低轨卫星导航增强系统,ICR越大,隔离效果越好。
4.1 参数设置
采用GPS信号作为导航增强载荷正常接收的信号,即期望信号,自干扰信号采用与期望信号伪码不同的GPS信号,并设信干比(Signal-to-Interference Ratio,SIR)为-70 dB,信噪比(Signal-to-Noise Ratio,SNR)为-20 dB,载波频率为80 kHz,采样率为400 kHz,使用QPSK进行调制,不考虑非线性和ADC量化噪声的影响。参考文献[15],将自干扰信道设置为莱斯信道,传播路径个数为4,包括3条多径,对应的K因子、路径延时和损耗分别为[1 2 0.5 0.02],[2.5 4 7 10]×ts,[-15 -29 -46 -53],其中ts为fs的倒数,fs为采样率。根据先验知识,本文设置自干扰估计信道的冲激响应的阶数为20。为了表示收敛速度,更直观地体现算法收敛性,将ICR曲线中的横坐标迭代次数n等价转换为时间t,其中t是由n和ts相乘得到。本节所有结果均是由200次蒙特卡罗仿真实验所得。
在上述仿真条件下,将本文提出的IVSSLMS算法与文献[15,19-20]中的变步长LMS算法进行比较。依据文献[15,19-20]中参数设置的原则,对这3种算法的参数进行适当的调整,以上4种算法的具体参数如表1所示。

表1 各算法对应的参数取值
4.2 收敛速度和干扰对消比性能分析
通过统计平均200次独立仿真结果,得到在参数(1)和参数(2)条件下IIVSSLMS算法与已有的3种变步长LMS算法性能对比结果如表2所示,在不同参数下4种算法的ICR收敛曲线分别如图5和图6所示。
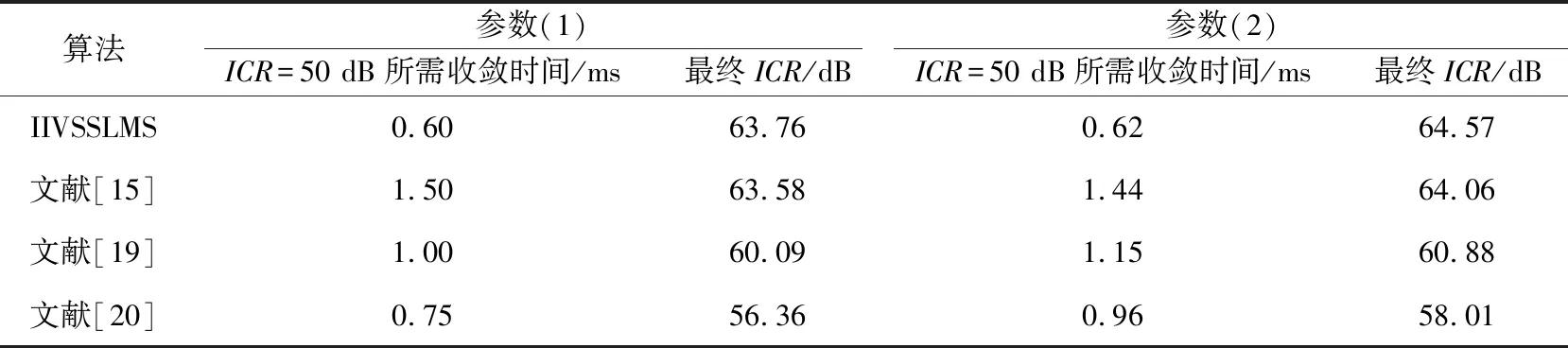
表2 算法性能对比
综合图5和表2可以得出,在参数(1)条件下,IIVSSLMS稳态的ICR为63.76 dB,略低于式(21)的理论值,IIVSSLMS与文献[15]相比,稳态的ICR仅提高了0.18 dB,但是IIVSSLMS在ICR=50 dB时所用时间比文献[15]缩短0.9 ms,收敛速度提高了2.5倍;与文献[19-20]相比,稳态的ICR分别提高了3.67,7.4 dB,在ICR=50 dB时所用时间分别缩短0.4,0.15 ms。综合图6和表2得出,在参数(2)的条件下,IIVSSLMS与文献[15]相比,稳态的ICR提高了0.51 dB,在ICR=50 dB时所需时间缩短了0.82 ms;与文献[19-20]相比,稳态的ICR分别提高了3.69,6.56 dB,在ICR=50 dB时所用时间分别缩短了0.53,0.34 ms。IIVSSLMS和文献[15,19-20]中的算法相比,在收敛速度和对消比上均占有一定的优势,这是由于本文所提IIVSSLMS算法在初始阶段设置步长因子为较大值,提高了收敛速度;之后由迭代次数和当前误差信号与上一步误差信号之间的自相关估计协同控制步长因子,使步长因子维持在一个较小的范围内,减小了系统的稳态误差。

图5 参数(1)对应的4种算法ICR曲线Fig.5 ICR curves of four algorithms corresponding to parameter (1)
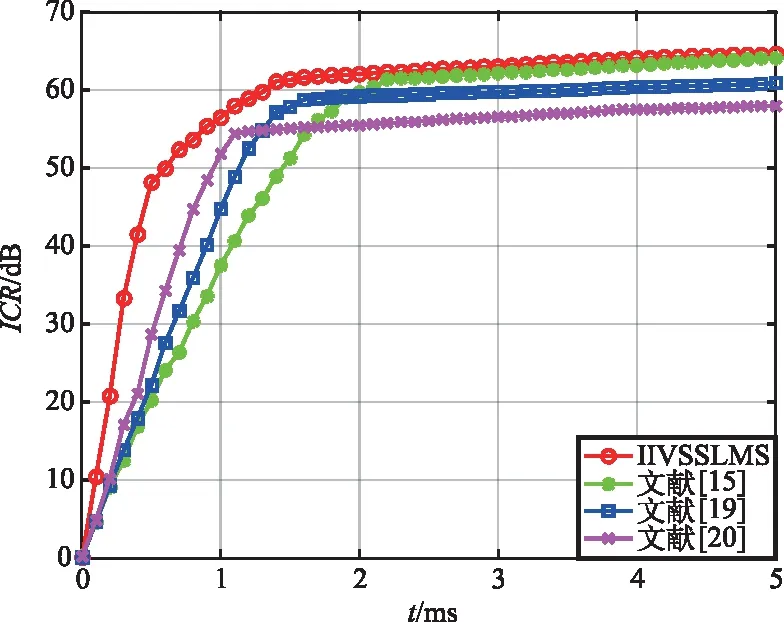
图6 参数(2)对应的4种算法ICR曲线Fig.6 ICR curves of four algorithms corresponding to parameter (2)
5 结束语
本文提出了一种基于IIVSSLMS数字域自干扰对消算法,可以有效消除低轨卫星导航增强系统中的自干扰。该算法利用迭代次数和当前误差信号与上一步误差信号的自相关估计共同调节步长因子,使步长因子在初期为较大值,之后保持在较小的范围内,很好地平衡了收敛速度和稳态误差,并通过不断地更新自干扰信道冲激响应,来获得最佳的自干扰信道参数,提升干扰对消性能。为了体现算法的有效性,本文与已有变步长LMS算法进行了比较,仿真结果表明收敛速度可以提高2.5倍,干扰对消比可以提高7.4 dB。在下一步工作中,将在数字域中考虑ADC器件造成非线性影响的同时,结合模拟域和空域因素,研究低轨卫星导航增强系统中的自干扰对消。
