关于新人教版“光的干涉”中的两点讨论
2022-09-08江苏苏州市第五中学校215000
江苏苏州市第五中学校(215000)施 音
在高中阶段,光的干涉现象是带领学生初步认识光的本性(即波粒二象性)的重要知识点之一。干涉是波独有的特征,在两列或几列波相互叠加的区域,出现某些区域始终振动加强,某些区域始终振动减弱,空间形成稳定的强弱分布规律。在双缝干涉实验中,光透过双缝在屏上显示出稳定的明暗相间的条纹,即光的干涉现象,也就证明了光具有波动性。
一、提出问题
新人教版高中物理选择性必修一在“光的干涉”一节中解释干涉条纹和光的波长之间的关系时(如图1),利用光程差r2-r1近似等于得出当两列波的光程差为波长整数倍,即=nλ(n=±0,1,2,3,…)时,出现亮条纹。亮条纹中心的位置为x=,相邻两条亮条纹或暗条纹的中心间距为Δx=。
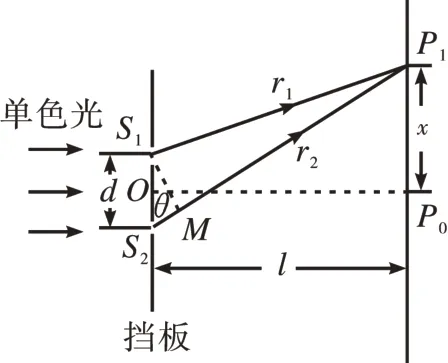
图1
这样的编写容易使学生产生两点误解:(1)判定出现亮条纹的条件=nλ(n=±0,1,2,3,…)中n的取值范围是整数集;(2)相邻两条亮条纹或暗条纹的中心间距为Δx=,由λ、l、d 决定,都与亮条纹的位置x无关,即条纹是等间距分布的。
二、分析说明
既然光程差δ=|r1-r2|决定了振动由双缝S1,S2传到空间某点P1叠加后的结果,△S1S2P1必须满足两边之差小于第三边的原理;另一方面屏上第n级亮条纹,即为S1,S2到该处光程差为波长的n倍,也就是同级亮条纹应当出现在以S1,S2为焦点的双曲线上,因此可以根据双曲线方程来计算光屏上的条纹间距。以下为详细说明。
双缝干涉是利用单缝输入光波的波阵面在双缝处分成两列子波,形成相干光源,在叠加区域出现干涉现象,这种产生相干光源的方法称为分波阵面法。若单缝S0到两双缝S1,S2的距离相等,则分出的两列子波初相位相同,由双缝到叠加区域固定点间的光程差决定相位差。(如图2)
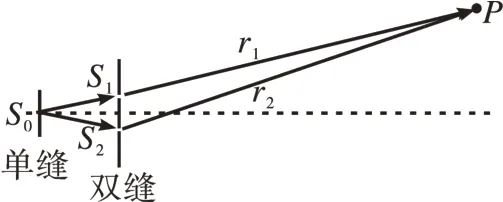
图2
设在S1,S2处两列子波的振动方程为y=Asin(ωt+φ),波速为v,空间P点到双缝S1,S2的距离分别为r1,r2,则两列子波在空间P点引起的振动方程分别为,P点实际的振动满足两列子波在P点引起振动的矢量叠加原理。在P点便出现频率相同、初相位不同的振动叠加。在频率相同的情况下,两个振动的相位差是恒定的,即能够形成稳定的干涉图样。当它们的相位差满足π 偶数倍时,P点合振幅最大;当相位差满足π 奇数倍时,P点合振幅最小。从光程差的角度来说就是:
δ=|r1-r2|=nλ(n=0,1,2,3,…)时,P点振动加强为明条纹中心;
δ=|r1-r2|=(2n+1)(n=0,1,2,3,…) 时,P点振动减弱为暗条纹中心。
从上述分析可以看出,明暗条纹的出现是由于光程差等于半波长的偶数倍或者奇数倍,而我们通常说的第n级明条纹就是指双缝到该点光程差是波长的n倍。因此,同级亮条纹应当出现在以双缝为焦点的双曲线的半支。
设双缝S1、S2间距为d,亮纹所在的双曲线族标准方程为=1(n=1,2,3,…),
亮条纹所在的双曲线族渐近线方程为y=±x(n=1,2,3,…)
亮条纹级数越高,对应渐近线斜率越大。(如图3)
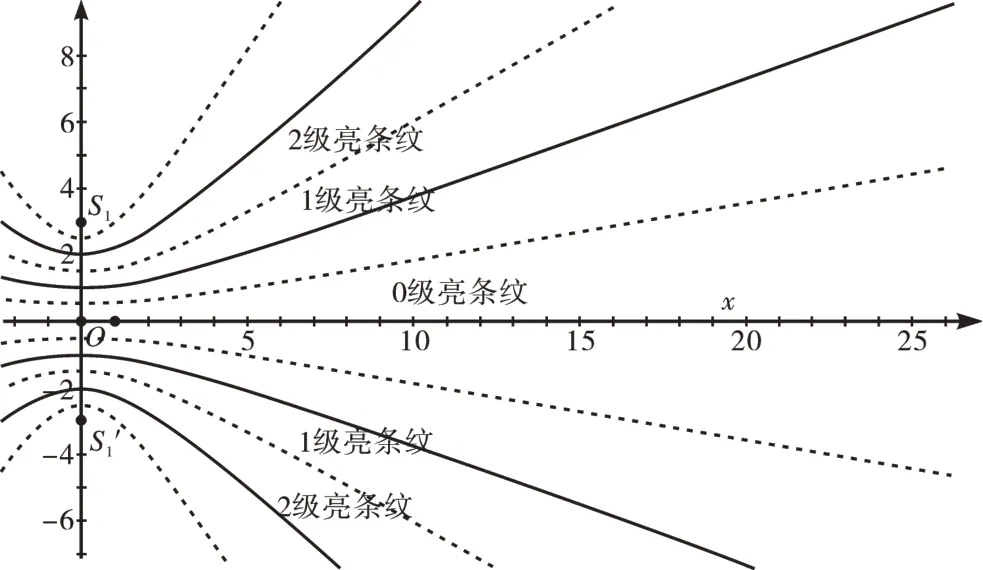
图3
(一)误区一:n取值为自然数集
在△S1S2P中|r1-r2|<d,因此空间P点的最大光程差为d,亮条纹最高级为(取整数部分)。
亮条纹级数n的取值是范围在的自然数。
(二)误区二:与双缝平行的屏上,条纹等间距分布
设离双缝距离为l处有一与双缝平行放置的光屏,若满足d≪l,则屏上显示的条纹间距可以近似由双曲线渐近线方程求得:
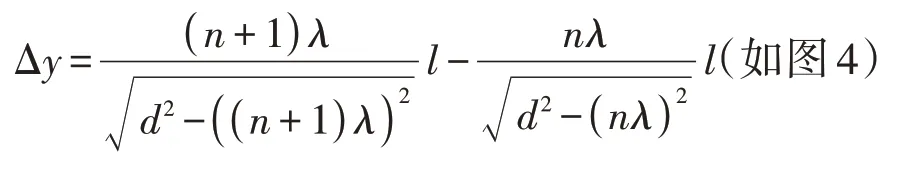

图4
(关于图4 的说明:光屏和双缝的距离一般是双缝间距103倍,此处只是示意图,用于说明同级亮条纹所在的双曲线,在到达光屏时已经很接近渐近线,因此可以由双曲线的渐近线方程计算条纹间距。)
当亮条纹级数较低时,由于双缝间距d和光波波长λ 相差103倍,忽略高阶无穷小项,可近似求得,即条纹等间距分布。
当亮条纹级数接近最大级时,条纹间距不相等。
三、应用
[例1]在双缝干涉实验中,用绿色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是( )。
A.改用红色激光
B.改用蓝色激光
C.减小双缝间距
D.将屏幕向远离双缝的位置移动
E.将光源向远离双缝的位置移动
F.将光源略偏向双缝中的某一条移动
解析:在亮条纹级数不太大的情况下,我们可以用条纹间距Δx=来判断。要使条纹间距变大,可以通过增大波长λ、减小双缝间距d、增大光屏和双缝距离l来实现。即A,C,D正确,B错误。

图5
使光源远离双缝,并不改变亮条纹的双曲线族标准方程(2a=nλ,2c=d),光屏到双缝的距离不变,即由渐近线方程计算得到的条纹间距也不变。E错误。
使光源略偏向双缝中的某一条(如图5),设光源S0到双缝S1,S2的距离之差为δ0=S0S2-S0S1,显然0 级亮条纹将不在双缝中垂线上,而是略向下移动。仍然以S1,S2为双曲线焦点,则亮条纹的双曲线方程族应修正为(2a=nλ±δ0(P点出现在双缝中垂线下方为“+”,上方为“-”),2c=d),通过渐近线方程求得屏上条纹间距为Δy=l(双缝中垂线下方为“+”,上方为“-”)。同样在条纹级数不大的情况下,条纹间距可以近似等于Δy=,即条纹间距不变。F错误。
答案:ACD
四、反思
我们在日常教学中强调对明暗条纹的判断,而忽略了对条纹定级的解释。其实对条纹级数的理解能够在解决诸如条纹的移动、条纹间距变化等动态问题上提供很大的方便,便于学生理解。
在薄膜干涉问题中,入射光在透明薄膜上下两表面的反射光在空间相遇产生干涉现象,其光程差近似等于薄膜厚度的两倍(如图6)。
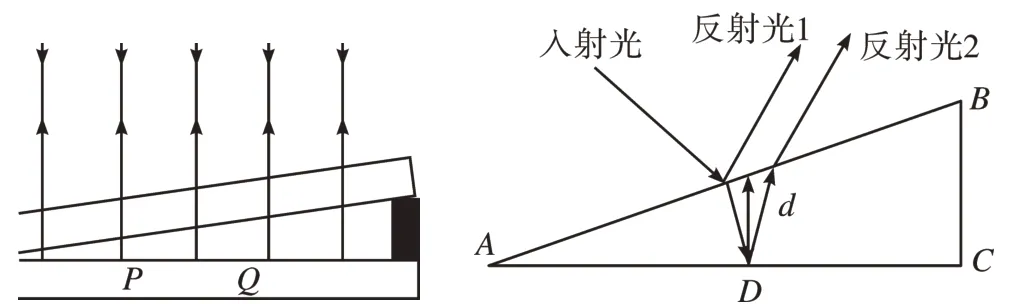
图6

图7
若增加BC端的厚度,即θ变大,则条纹级数增大,可以观察到条纹间距变小,条纹向劈尖移动。
若观察到的条纹间距不相等,则说明薄膜厚度变化不均匀。
[例2](2021年高考山东卷第7题)用平行单色光垂直照射一层透明薄膜,观察到如图8 所示明暗相间的干涉条纹。下列关于该区域薄膜厚度d随坐标x的变化图像,可能正确的是( )。

图8
解析:可以理解为条纹间距变大,说明条纹级数随距离变化变缓(如图9)。

图9
答案选D。
