An Extended Convex Combination Approach for Quadratic L 2 Performance Analysis of Switched Uncertain Linear Systems

Yufang Chang， Guisheng Zhai，，，Lianglin Xiong， and Bo Fu

Dear Editor，

There have been a few references studying quadratic stability/stabilization of switched certain linear systems. Reference [1]， [2] show that if there exists a stable convex combination of subsystem matrices， then a state-dependent switching law can be proposed with a quadratic Lyapunov function to stabilize the switched system. Reference [3] investigates quadratic stability/stabilization of a class of switched nonlinear systems by using a nonlinear programming(Karush-Kuhn-Tucker condition) approach. Reference [4] extends the discussion and results in [1]， [2] to achieve quadratic stability for switched linear systems with norm-bounded uncertainties， and a state-dependent switching law has been proposed for quadratic stabilization. Recently， [5] extends the discussion and results in [1]， [2]，[4] to output dependent switching law design for quadratic stabilization of switched linear systems with norm-bounded uncertainties. In both [4] and [5]， a matrix inequality approach is used for the convex combination of subsystems to design the Lyapunov matrix in the switching law. Note that the motivation of dealing with switched uncertain systems is both theoretical and practical， when a single uncertain subsystem can not achieve certain desired performance.

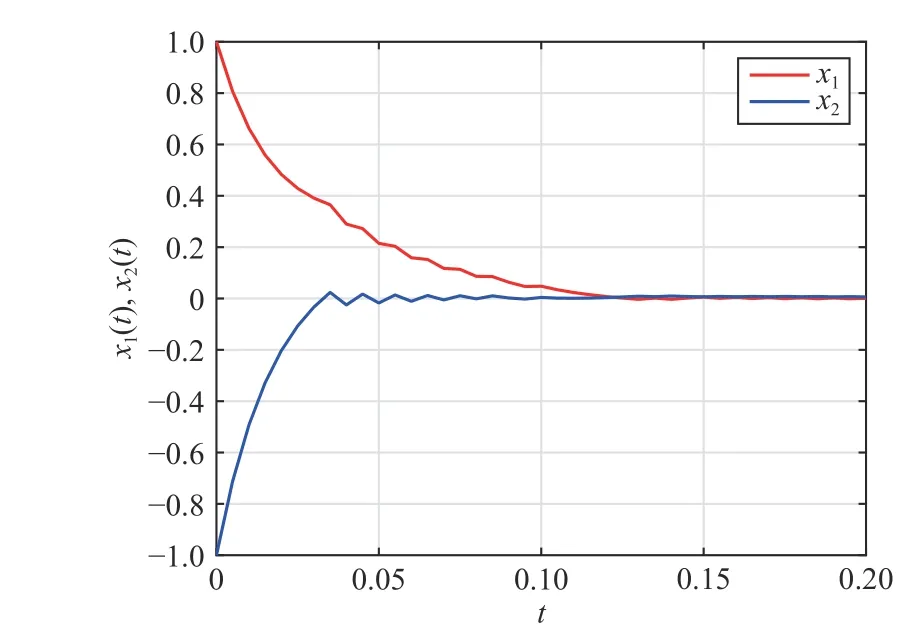
Fig. 1. State trajectories in the numerical simulation.