Efficient Exploration for Multi-Agent Reinforcement Learning via Transferable Successor Features

Wenzhang Liu， Lu Dong，，， Dan Niu，，， and Changyin Sun， Senior，

Abstract—In multi-agent reinforcement learning (MARL)， the behaviors of each agent can influence the learning of others， and the agents have to search in an exponentially enlarged joint-action space. Hence， it is challenging for the multi-agent teams to explore in the environment. Agents may achieve suboptimal policies and fail to solve some complex tasks. To improve the exploring efficiency as well as the performance of MARL tasks， in this paper， we propose a new approach by transferring the knowledge across tasks. Differently from the traditional MARL algorithms，we first assume that the reward functions can be computed by linear combinations of a shared feature function and a set of taskspecific weights. Then， we define a set of basic MARL tasks in the source domain and pre-train them as the basic knowledge for further use. Finally， once the weights for target tasks are available， it will be easier to get a well-performed policy to explore in the target domain. Hence， the learning process of agents for target tasks is speeded up by taking full use of the basic knowledge that was learned previously. We evaluate the proposed algorithm on two challenging MARL tasks: cooperative boxpushing and non-monotonic predator-prey. The experiment results have demonstrated the improved performance compared with state-of-the-art MARL algorithms.

I. I NTRODUCTION

REINFORCEMENT learning (RL) has made great success recently in various sequential decision-making problems， such as video games [1]， [2]， continuous control [3]–[5]， and navigations [6]–[8]， etc. However， there exist challenges of extending the RL algorithms from single agent to multi-agent systems (MAS)， where multiple agents behave together in a common environment to achieve cooperative and(or) competitive tasks [9]. On the one hand， for each agent in an MAS， its local next-state distribution may be influenced by other agents， which will bring uncertainties to the agent when the policies of others are updated. Hence， the agents will encounter the challenge of non-stationarity during the learning process [10]–[13]. On the other hand， the joint-action space of an MAS will be enlarged exponentially as the number of agents grows. That will make it more difficult for agents to explore in the joint-action space， and the agents may fall into local optimal solutions or fail to solve the tasks [14]. For a practical example， there are two agents learning to push a heavy box cooperatively from one place to somewhere else.The box can be pushed to move if and only if two agents force it together. Agents should first catch the box cooperatively，and then push it to explore in the environment. When the environment is complex and the reward function is sparse， it will be hard for agents to find the target place where the box should be pushed into.

A direct idea of extending RL to multi-agent reinforcement learning (MARL) is independent learning [15]， [16]， in which every agent learns to search for the optimal solution without considering the policies of others. As is mentioned， that will cause non-stationarity of the next-state distribution. Hence， the paradigm of centralized training with decentralized execution(CTDE) is widely used to learn optimal joint-policies [17]，[18]. CTDE collects global information of all agents during training while executes actions according to the local observation of each agent. CTDE is useful to stabilize the training. However， a good exploring joint-policy is also important for an MAS with sparse rewards and continuous state and action spaces. Without useful data being collected during exploration， the algorithm may fall into the local optimal solutions and fail to accomplish the complex tasks.Inspired by the idea of transfer reinforcement learning (TRL)[19]， we propose to first learn some easier tasks as the basic knowledge， and then calculate a good initialized policy through knowledge transfer to guide the exploration [20]， [21].The TRL generalizes the algorithms across tasks by leveraging the knowledge learned in previous， which is different from the traditional RL algorithms that learn within tasks.

Previous work shows the successor features (SFs) based TRL algorithms can provide a good initialization for target tasks to speed up the learning [22]–[26]. SFs decouple the dynamics of the environment from the reward and value functions， so they can be seen as robust features to describe different tasks [27]. When the reward function of the environment changes， the value function for the target task can be calculated quickly. From that point of view， one can first learn some related and easier tasks， and then start the learning of complex target tasks with a good initialized policy to improve the exploration. Hence， in this paper， we aim to learn centralized SFs instead of critics to evaluate different tasks，and then improve the exploration efficiency for target tasks through knowledge transfer. The core hypothesis of SFs based RL algorithms is the reward functions can be combined linearly by a shared feature function (reward features) and a set of task-specific weight vectors. Thus， once we have learned the task weights in the target domain， it will be easier to get the values through linear combination with the SFs in the source domain. That is why the SFs-based RL benefits knowledge transfer across tasks.

Most of the existing SFs-based algorithms focus on single agent systems. Since each agent in an MAS behaves in a common environment， decoupling the dynamics of the environment from the reward and value functions could be useful to share the learning. Because the reward and value functions can be computed by linear combination， it is possible to deal with unseen tasks in target domain without learning from scratch. Taking the box-pushing as an example，the agents can first learn how to push the box cooperatively to some basic places， and store the SFs as source knowledge.Then， they can get the value functions of more complex tasks through linear combinations of the source SFs and the target task weights. Finally， it will be easier for agents to get a new policy with efficient exploring ability. In this paper， we aim to deal with the MAS problems with continuous action and state spaces. To learn a deterministic policy for each agent， the framework of multi-agent deep deterministic policy gradient(MADDPG) [28] is used to implement CTDE. Differently from the original MADDPG algorithm， we build a global successor feature network (GSFN) instead of multiple agentwise critic networks to evaluate the joint-policy. A shared GSFN can avoid recalculation of the iterative value functions for agents， and generalize the original MADDPG across different tasks. The main contributions of this paper are listed as follows:

1) We implement the MARL with continuous action and state spaces by applying the SFs to the MADDPG algorithm.A new algorithm called multi-agent deep deterministic policy gradient with successor features (MADDPG-SFs) is proposed.The critic networks in traditional MADDPG are replaced by a shared GSFN to evaluate the long-term accumulated features.The algorithm calculates the value functions of different tasks by linear combinations of the SFs and task-specific weights;

2) For the new and more complex tasks in the target domain， we improve the exploring efficiency of the MARL by transferring the knowledge that was learned before. A new algorithm called multi-agent deep deterministic policy gradient with successor features and knowledge transfer (MADDPGSFKT) is proposed. The algorithm takes full use of the knowledge in the source domain， and calculates a wellperformed joint policy to implement efficient exploration in the target environment.

The rest of the paper is organized as follows. The related work is introduced in Section II. Section III is about the research background and problem formulation. The details about our proposed algorithms are provided in Section IV.Section V shows the simulation results to verify the proposed algorithms. Finally， the conclusion is drawn in Section VI.

II. RELATED WORK

Recently， the successes of deep RL in single agent systems have raised increasing interest in MARL. For example，Tampuuet al.[16] directly extended the deep Q-learning(DQN) [1] to MASs， and trained each agent via independent Q-learning (IQL). IQL learns without considering the information of others， which may leads to non-stationarity and local optimal solutions [10]， [11]. To solve that problem， the CTDE based learning framework is proposed to stabilize the learning， such as value decomposition networks (VDN) [29]，Q-mixing (QMIX) [30]， MADDPG [28]， etc. The VDN and QMIX are both value based algorithms like IQL. Hence， they cannot provide deterministic policy for each agent with continuous action space. Besides， the calculation of the holistic Q-values in VDN or QMIX has limited the representations of the Q-functions. Differently from that，Loweet al.[28] proposed MADDPG which was based on actor-critic and policy gradient algorithms. MADDPG collects the observations and actions of all agents to approximate the Q-value of each agent through a critic network. The policies are approximated by agent-specific actor networks. It could be an idealized setting for MARL， especially for learning deterministic policies with continuous action spaces. To make agents cooperate with each other more efficiently， Maoet al.proposed attention MADDPG (ATT-MADDPG) [31]. ATTMADDPG enhances the centralized critic with an attention mechanism to model the policies of the teammates. However，the MADDPG-based algorithms still have limitations of exploration for complex tasks and sparse rewards.

Existing research suggests that TRL can reduce the exploration of target tasks， and avoid learning from scratch compared with traditional RL algorithms [19]–[21]. In MARL，transferring knowledge across agents [32] and tasks [33]， [34]plays an important role in generalizing the algorithms to the target domain. For instance， Yanget al.[35] proposed multiagent option-based policy transfer (MAOPT) to learn when to transfer knowledge among agents. In [36]， Omidshafieiet al.learned multiple tasks for agents with partial observation through a distilling policy. However， these TRL methods extract the knowledge from the behaviors of agents， which cannot describe the relationships between the source tasks and the target tasks. By assuming the dynamics of the environment is unchanged， and the tasks differ only in the reward functions， the idea of SFs is used to extract the useful knowledge of transferring for the target tasks.

In [37]， Dayan expressed the Q-value as an inner product of the immediate reward function and the proposed successor representation (SR). The SR is defined as a cumulative of discounted future states [37]， [38]. SR is seen as a third alternative of RL algorithms following the model-based and modelfree RL [22]. In [22]， Kulkarniet al.presented deep SR (DSR)to implement the end-to-end deep reinforcement learning.Barretoet al.extended the idea of SR from discrete to continuous spaces， and proposed the successor features and generalized policy improvement (SF&GPI) algorithms for TRL to improve the learning of unseen tasks [23]， [26]. In[24]， Barretoet al.further generalized the SF&GPI to any set of tasks， and used the reward functions in source domain as the features of target rewards. Hence， we can build the source tasks through some basic tasks， and then form the reward features of target tasks， such as [25]. By applying the DSR and decoupling the option-value functions， Yanget al.[35]also proposed MAOPT with successor representation option(MAOPT-SRO) to learn what advice to provide and when to terminate it during the knowledge transfer among agents. In order to improve the exploration of MARL， Guptaet al.[39]proposed the universal value exploration (UneVEn) algorithm by combining the multi-agent universal SFs and the generalized policy improvement. UneVEn samples a set of related tasks near the target task and learns these tasks simultaneously to achieve better coordination between agents.

In this paper， we develop a new MARL algorithm based on SFs. To improve the efficiency of the exploration for complex tasks， we first learn some basic tasks and build the reward features. Then we combine the SFs linearly with task weights to implement knowledge transfer.

III. PRELIMINARIES

In this section， we introduce the background and problem formulation about reinforcement learning， multi-agent reinforcement learning， and the successor features for transfer reinforcement learning.

A. Reinforcement Learning

Q*(s，a)=r+γQ*(s′，π*(s′)). (1)

There are many advanced RL algorithms aiming to findπ*andQ*which satisfy (1)， such as deep Q-learning (DQN) [1]，deep deterministic policy gradient (DDPG) [3]， and soft actorcritic (SAC) [41]， etc.

B. Multi-Agent Reinforcement Learning

C. Successor Features for Transfer Reinforcement Learning

In order to learn transferable features across different tasks for an RL agent， we first decompose the reward function as a linear combination with the following assumption [23]， [26].

Thus， we get a transferrable policy across the whole task space. (6) is called the SFs&GPI policy， which combines the SFs and GPI to achieve a policy with good jump-start of performance for the target task [23]， [24].

IV. MULTI-AGENT REINFORCEMENT LEARNING AND TASK TRANSFER WITH SUCCESSOR FEATURES

In this section， we first extend the idea of successor features from the discrete action space and single-agent RL to continuous action spaces and MARL， respectively. Then， we propose an SFs-based learning algorithm for MARL. Finally，we extend the algorithm to make the agents learn target tasks by transferring the knowledge of source domain.

A. Multi-Agent Reinforcement Learning via Successor Features

During the agents-environment interaction， we store the reward data to the replay buffer. Then， we approximate the reward function in (9) by minimizing

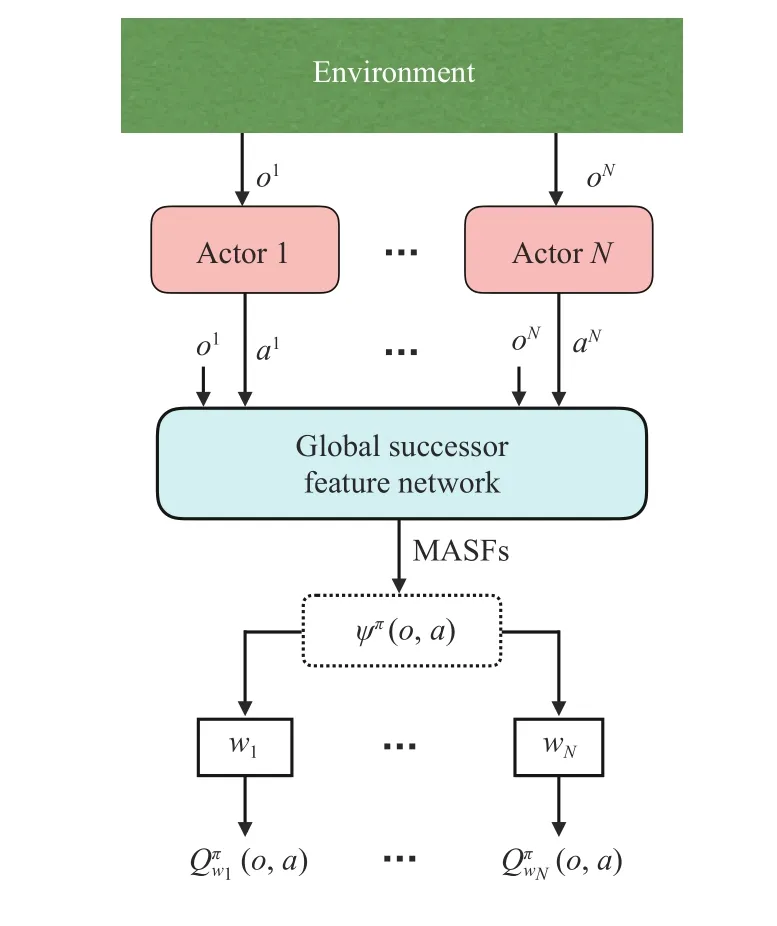
Fig. 1. Framework of MADDPG-SFs algorithm. The Q-values are computed by linear combinations with MASFs and task-specific weights. The MASFs are approximated by the GSFN.

Algorithm 1 MADDPG-SFs Require: Episode number ， mini-batch size ， discount factor γ，learning rate ， soft-update factor τ.episode=1 Ne Ne Nb αψ， αw， απ 1: for to do{oi0}Ni=1←2: Reset environment: initial observations.3: for to do ait ←πi(oit) i=1，...，N.4: ，t=0 T-1 5: Execute ， then we get and φt+1 ←φ(ot，at，ot+1).at{oit+1}N }N i=1{rit+1 i=1.6: Calculate features＜{oit，ait，oi t+1，rit+1}N 7: Append to Nb D.i=1，φt+1 ＞ D.8: Sample transitions randomly in θψ ←θψ-αψ∇Lψ.9:10:θψ，tar ←τθψ+(1-τ)θψ，tar.11: for to N do wi ←wi-αw∇Liw.12:θiπ ←θiπ+απ∇θiπJi(θiπ).13:i=1 θiπ，tar ←τθiπ+(1-τ)θiπ，tar.14:15: end for oit ←oit+1， ∀i=1，...，N.16:17: end for 18: end for

Differently from the single-agent RL， the CTDE is applied in MADDPG-SFs. During centralized training， the algorithm aims to learn a vector function ψ*(o，a) rather than a scalar functionQ*(o，a). While in decentralized execution， the policy of each agent takes only its local observation as input to explore in the environment. It should be noted that the reward weightswiare not always agent-wise. When a multi-agent team aims to achieve common goals (cooperative tasks)， the agents share one weight to learn optimal policies.

B. Knowledge Transfer for Target Tasks

Algorithm 2 MADDPG-SFKT{π*j}M1 {ψπ*j}M1 Nt Nb αψ，αw，απ Require: ， for M basic tasks， episode number ， minibatch size ， discount factor γ， learning rate ， soft-update factor τ.episode=1 Nt 1: for to do{oi0}Ni=1←2: Reset environment: initial observations.3: for to do at=(a1t，...，aNt )←π′(ot).4:at {oit+1}Ni=1 r′t+1.5: Execute ， then we get and t=0 T-1 6: Calculate features＜{oit，ait，oi φt+1 ←φ(ot，at，ot+1).i=1，r′t+1，φt+1 ＞ D′.7: Append to t+1}N Nb D′.8: Sample transitions randomly in w′←w′-αw∇Lw′.9:θ′ψ ←θ′ψ-αψ∇L′ψ.10:θ′ψ，tar ←τθ′ψ+(1-τ)θ′ψ，tar.11:12: for to N do θiπ′ ←θiπ′-απ∇Liπ′.13:i=1 14: end for oit ←oi t+1，∀i=1，...，N.15:16: end for 17: end for

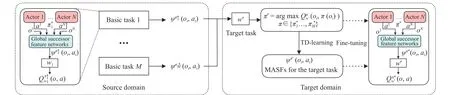
Fig. 2. Framework of the learning for π* and Qπw*′. Left part represents the source domain， which contains the basic tasks learned previously. Right part represents the learning process for the more complex target task in the target domain.

C. Theoretical Analysis of the Jump-Start Policy π′

V. SIMULATION

In this section， to verify the theoretical analysis in section IV， we evaluate the performance of proposed algorithms on two challenging multi-agent simulation environments. All simulations are run at a desktop with Intel Core i7-7700k CPU@4.20GHz under Ubuntu 18.04 operation system2The code is available at: https://github.com/wenzhangliu/maddpg-sfkt.git.

A. Environments

1) Cooperative Box-Pushing:In a cooperative box-pushing environment， two agents aim to push a box to the target position cooperatively. As shown in Fig. 3(a)， the target position is on the right part of the environment， while the box is started in the left area. Between the target and the start point of the box， there are two additional objects (obstacles) that should be avoided by the box. The box can be pushed to move if and only if two agents force it concurrently， which makes it more challenging for the box to explore the target position in the environment3The video of the simulations: https://youtu.be/w0kscgRTGz8. The observation spaces for agents are continuous， which include the information about the positions of all entities， as well as the velocities of the agents and the box. Agents take continuous actions varying from -1 to 1 on both horizontal and vertical directions. To guide the agents to move toward the box， one agent will get a +1 reward if it catches the box. The agents will get a +5 reward if the box covers the target object on the right area， but they will be penalized withrpif the box meets an obstacle. In the next part， we will show how differentrp∈{0，-0.5，-2.5，-5.0} influence the learning performance of the compared algorithms.Agents will also be penalized by -1 if they collide with each other or the wall， or if the box is pushed to the wall. As one can see， the reward of +5 is sparse for the two agents， which makes it more difficult to explore and learn the task.(PID) controller separately.

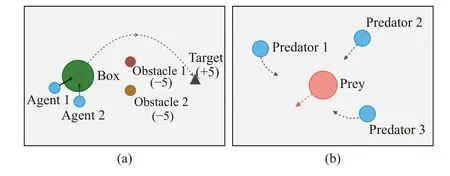
Fig. 3. The simulation environments: (a) Cooperative box-pushing; (b) Nonmonotonic predator-prey.

B. The Design of the Featuresφ

C. Simulation Results and Discussions

In the experiments， we adopt deep neural networks with two hidden layers and three hidden layers to approximate the actor networks and the GSFN， respectively. Each hidden layer is non-linearized by a leaky rectified linear units (ReLU)activation function [49]. The output layer of each actor network is activated by a tanh-function， which guarantees the actions to be continuous and bounded in [ -1，1]. The last layer of GSFN includesdnodes without activation function， wheredis the dimension of φ. Details of the learning settings for the two environments are listed in Table I. In the following experiments， the MADDPG-SFKT contains the fine-tuning steps as shown in Fig. 2. Since the action spaces are continuous in the two simulation environments， the proposed algorithms are compared with MADDPG [28]， ATTMADDPG [31]， MAOPT-SRO [35]， and UneVEn [39]. We replicate the MAOPT-SRO based on MADDPG framework with the same experiment settings in [35] for fairness. To implement the value-based UneVEn in continuous action spaces， we discretize the two dimensional continuous actions as { [0，0]，[0，-1.0]，[0，1.0]，[-1.0，0]，[1.0，0]}.

rp=0w′=w2=[0，0，1，1]T

When ， i.e.， ， we compare the MADDPG-SFs with the other algorithms in Fig. 4(a). It isfound that the MADDPG-SFs fails to outperform the other algorithms， because it learns thew′from scratch. However， it can converge to the near optimal solutions， which can be used to collect the knowledge in source domain. If we add the penalty (e.g.，rp=-0.5)， there will be significant performance decline of the baseline algorithms (as shown in Fig. 4(b)).MADDPG-SFKT can achieve the optimal solutions after 1000 episodes， while the other MADDPG-based algorithms can not converge until 4000 episodes. In Figs. 4(c) and 4(d)， we can find that the compared baselines converge to suboptimal solutions when the |rp| increases. As for UneVEn， it performs worst compared with other methods in this environment. The UneVEn learns a set of related tasks simultaneously to improve the exploration， however， the reward for target task is too sparse for the agents to achieve. Although the MADDPGSFKT performs worse at the early training stage， it can achieve more accumulative return in the long run. As shown in Fig. 5， whenrp≤-0.5， the best trained MADDPG-SFKT models always outperform the other methods. Whenrp=0，-0.5， or -2.5， the ATT-MADDPG can sometimes improve the cooperation of agents with the attention mechanism， while its performance is unstable and limited.

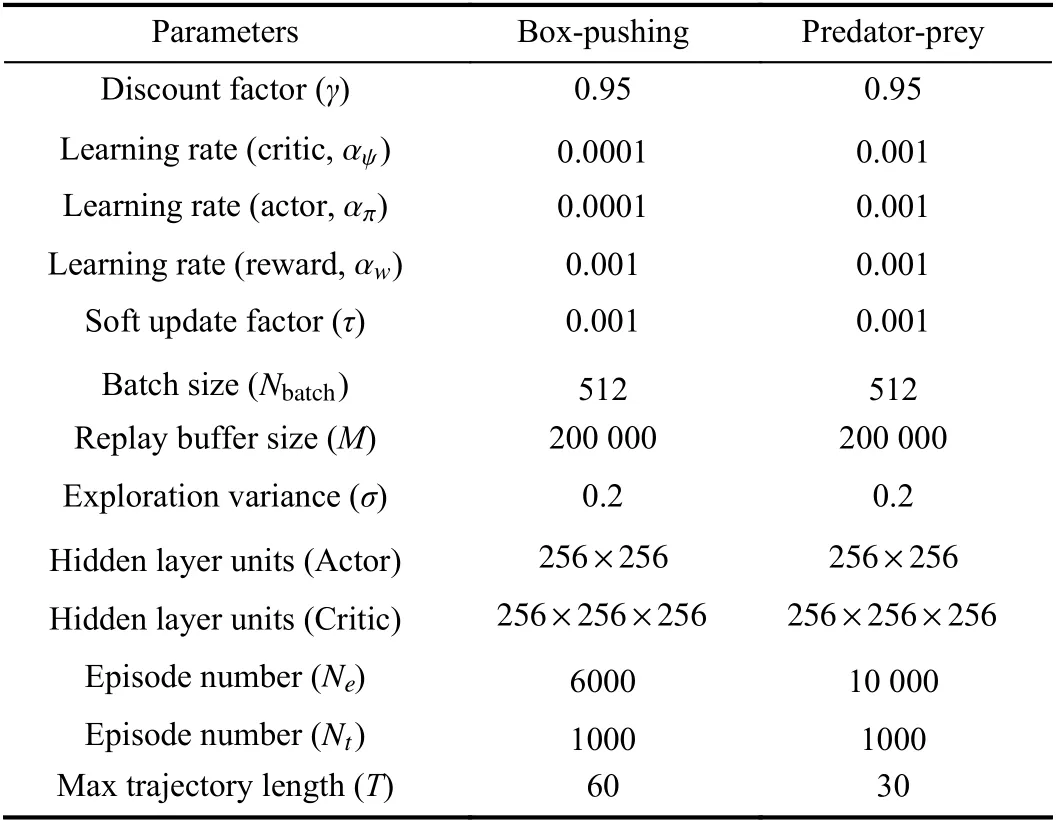
TABLE I PARAMETER SETTINGS FOR TWO SIMULATIONS

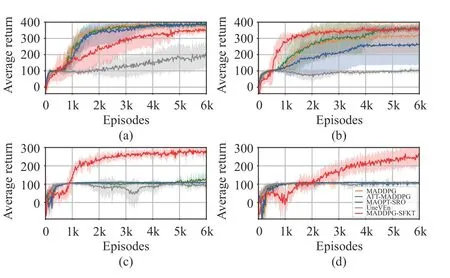
Fig. 4. The cooperative box-pushing simulation results with different obstacle penalties. (a) r p=0 ; (b) r p=-0.5 ; (c) r p=-2.5 ; (d) r p=-5.0.

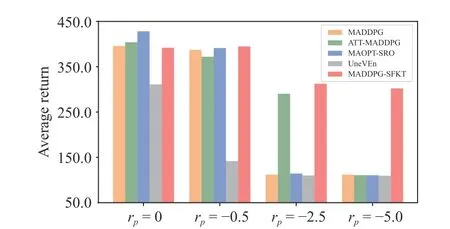
Fig. 5. The compared average return of the models for box-pushing that perform best in ten random seeds.

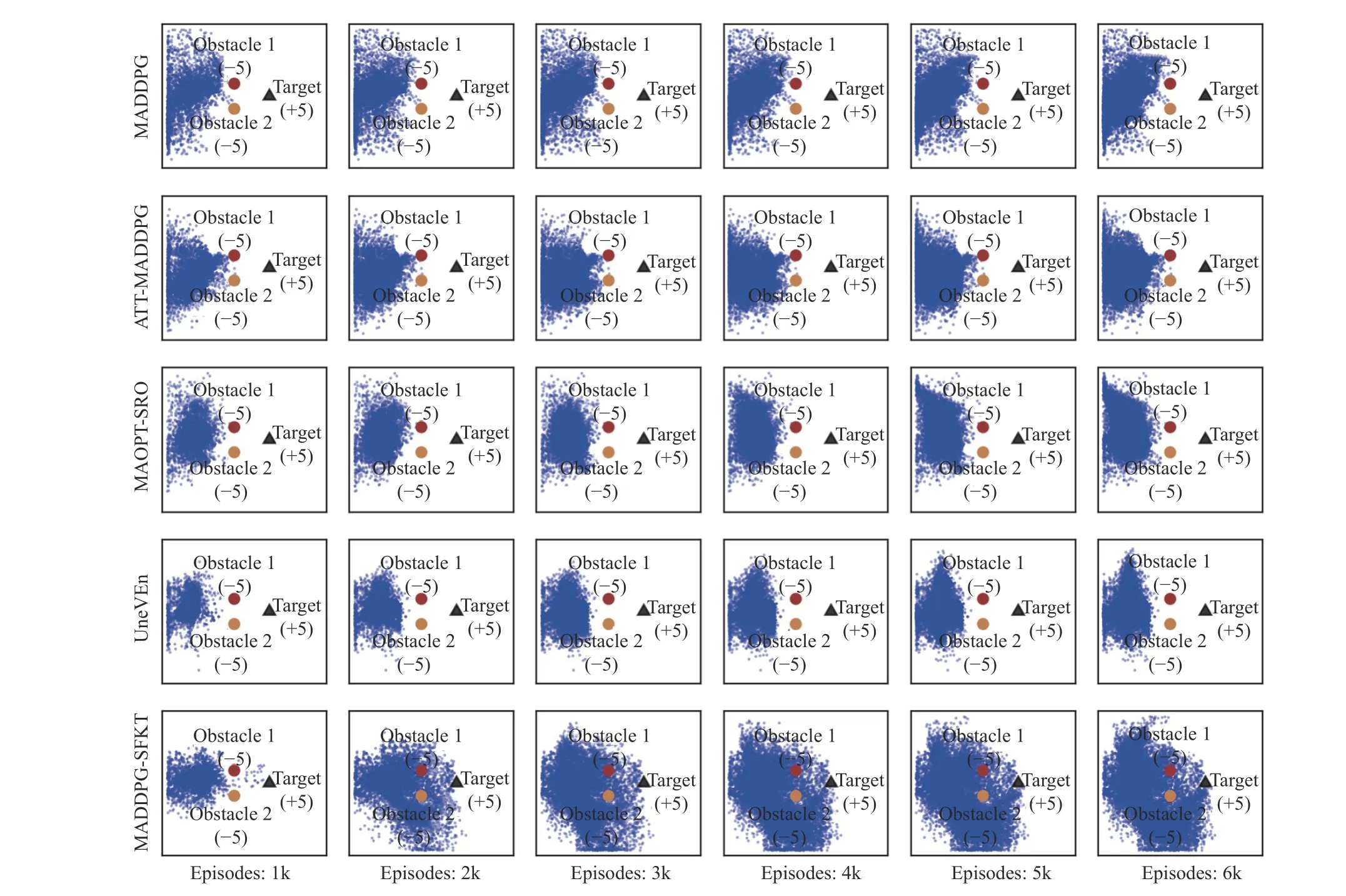
Fig. 6. The states visited at different training steps during exploration for cooperative box-pushing simulation.

To show the exploration process， we plot the states visited by the box during the training in Fig. 6. When the box collides with any of the two obstacles， two agents will be penalized withrp=-5.0. Hence， the two obstacles block the way from start position to the target position for the box. It is found that the other methods are hard to explore in the right area of the environment. If we use π′calculated by (19) as the jumpstart policy， the agents can push the box to the target position at early training stage. For example， when the training episode is 1000， 2000， or 3000 in Fig. 6， the agents with MADDPGSFKT algorithm can push the box to visit the target position even if they would get immediate penaltyrp=-5.0. To get more positive rewards at the target position in the long run，our algorithm keeps exploring the optimal path to push the box from start position to the target. That is why the performance of MADDPG-SFKT is worse than the other methods at the fist 1000 and 2000 episodes in Figs. 4(c) and 4(d)， respectively. By taking full use of the knowledge in source domain， the MADDPG-SFKT shows more efficient exploration compared with other methods.

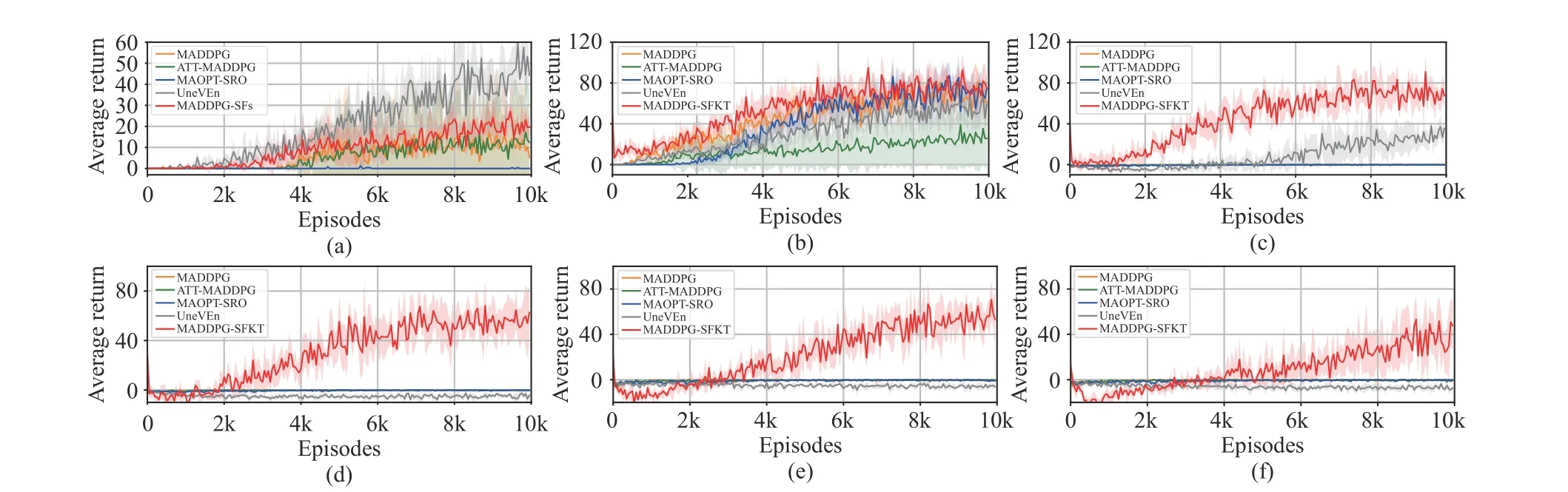
Fig. 7. The non-monotonic predator-prey simulation results with different groups of penalties， where the prey is controlled by random policy. (a)rp1 =0，rp2 =0 ; (b) r p1 =0， rp2 =1; (c) r p1 =-1， rp2 =1; (d) r p1 =-1， rp2 =-1; (e) r p1 =-2， rp2 =-1; (f) r p1 =-2， rp2 =-2.

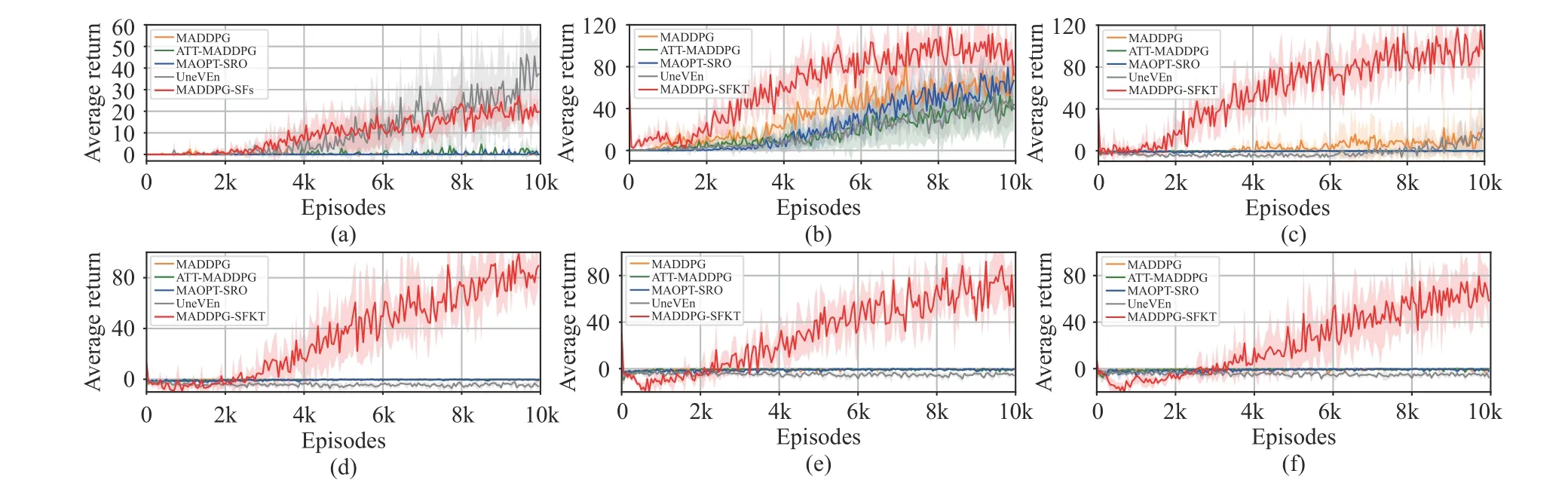
Fig. 8. The non-monotonic predator-prey simulation results with different groups of penalties， where the prey is controlled by pre-trained DDPG policy.(a) r p1 =0， rp2 =0; (b) r p1 =0， rp2 =1; (c) r p1 =-1， rp2 =1; (d) r p1 =-1， rp2 =-1; (e) r p1 =-2， rp2 =-1; (f) r p1 =-2， rp2 =-2.

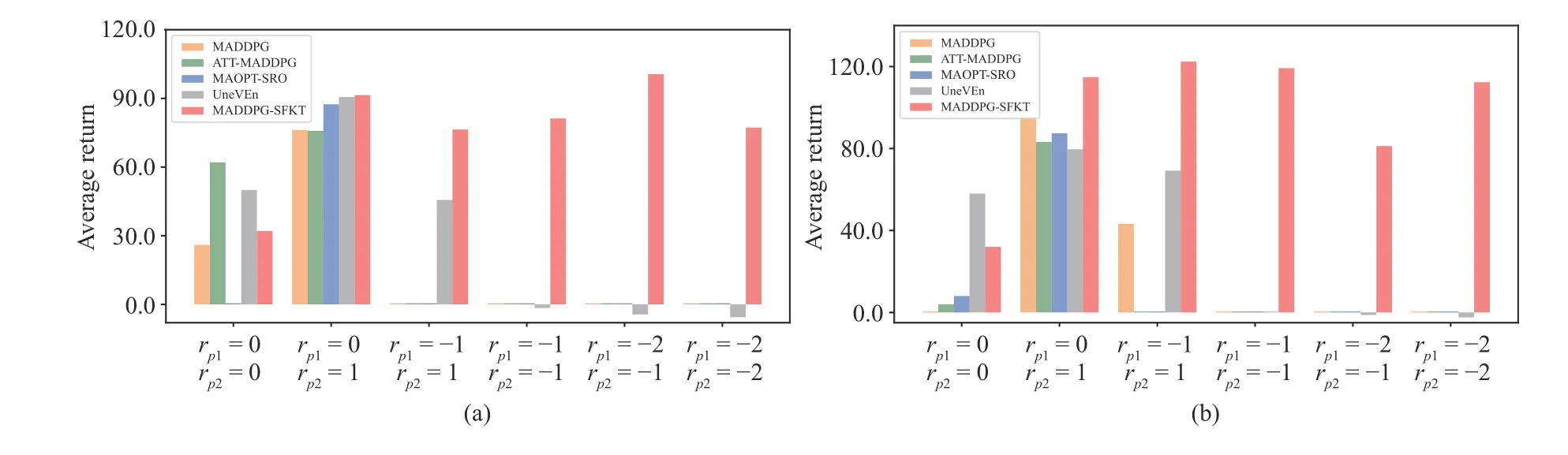
Fig.olicy and (b) DDPG policy.

It seems unfair for the other methods which learn from scratch without pre-trained models. However， because they cannot build the connections between the source domain and target domain， it is hard to get a pre-trained model which contains useful knowledge for learning different target tasks.In other words， these methods have to pre-train a model from scratch for each target task. Differently from that， once we have pre-trained these source tasks by MADDPG-SFs， we can use such knowledge to learn more different target tasks，without re-training the source tasks for each target task. That is why the proposed method outperforms the other methods on the challenging tasks.

VI. CONCLUSIONS

This paper proposes an SFs-based reinforcement learning method for cooperative MASs， which transfers knowledge from source tasks to the target task. A new multi-agent reinforcement learning framework with MASFs is introduced，which can learn not only joint optimal policies but also the MASFs and task weights. For more complex task in the target domain， traditional algorithms fail to find optimal solutions because of their limited explorations. With the MASFs and the corresponding policies learned in previous， the algorithm MADDPG-SFKT is proposed to take full use of the knowledge that was learned in the source domain， and explore more efficiently in the target environment. The theoretical analysis ensures the superiority of the exploring policy compared with the source policies， and also gives the performance bound. We evaluate the proposed algorithm in cooperative box-pushing and non-monotonic predator-prey environments. By increasing the difficulties in different simulation tasks， the experiment results have verified the proposed algorithm empirically and shown greater performance compared with state-of-the-art algorithms.