Autonomous Maneuver Decisions via Transfer Learning Pigeon-Inspired Optimization for UCAVs in Dogfight Engagements

Wanying Ruan， Haibin Duan，，， and Yimin Deng

Abstract—This paper proposes an autonomous maneuver decision method using transfer learning pigeon-inspired optimization (TLPIO) for unmanned combat aerial vehicles(UCAVs) in dogfight engagements. Firstly， a nonlinear F-16 aircraft model and automatic control system are constructed by a MATLAB/Simulink platform. Secondly， a 3-degrees-of-freedom(3-DOF) aircraft model is used as a maneuvering command generator， and the expanded elemental maneuver library is designed， so that the aircraft state reachable set can be obtained.Then， the game matrix is composed with the air combat situation evaluation function calculated according to the angle and range threats. Finally， a key point is that the objective function to be optimized is designed using the game mixed strategy， and the optimal mixed strategy is obtained by TLPIO. Significantly， the proposed TLPIO does not initialize the population randomly， but adopts the transfer learning method based on Kullback-Leibler(KL) divergence to initialize the population， which improves the search accuracy of the optimization algorithm. Besides， the convergence and time complexity of TLPIO are discussed.Comparison analysis with other classical optimization algorithms highlights the advantage of TLPIO. In the simulation of air combat， three initial scenarios are set， namely， opposite， offensive and defensive conditions. The effectiveness performance of the proposed autonomous maneuver decision method is verified by simulation results.

I.I NTRODUCTION

AIR combat， based on the size of aircraft， can be divided into one-to-one， one-to-multiple， multiple-to-multiple，and swarm-to-swarm air combat. One-to-one air combat，commonly known as a dogfight， is one of the most common and important combat form so far and the research background of this paper. Multiple-to-multiple and swarm-to-swarm air combat are the inevitable trend of air combat in the future，but also faces great challenges. Unmanned combat aerial vehicle (UCAV) can reduce casualties， and cope with harsh conditions， plays a leading role in the future air combat.Autonomy is the development direction of air combat in the future， and autonomous air combat involves a complex system， including situational awareness， maneuvering decisions and aircraft control. Among them， maneuvering decisions are the core of autonomous air combat， determining how to realize autonomous maneuvering decision for UCAV is a crucial and challenging issue.

The autonomous maneuver decision method can be roughly divided into three categories: mathematical solution， machine search， and data-driven method [1].

The mathematical solution method originated earliest. As early as in the 1990s， Isaacs [2] proposed the differential game， which was the earliest and most typical mathematical solution method and was widely applied to the pursuit-evasion problem. Later， a large number of scholars proposed improved algorithms. Baris and Emre [3] presented a differential flatness-based air combat maneuver strategy， where the differential flatness with receding horizon approach is used to generate an optimal feasible trajectory， which are parameterized through b-spline， and applied successfully to air combat between two UCAVs. The methods based on the mathematical solution are mathematically clear， but it is difficult to prove the adequacy and necessity of the mathematical solution. Moreover， its applicability is limited for complex air combat problems.

In terms of the machine search method， it is the most widely used and feasible air combat maneuvering decision method.Austinet al. [4] proposed the game-matrix approach， and adopted seven elemental maneuvers designed by National Aeronautics and Space Administration (NASA) to construct scoring matrix， where the minimax game algorithm is employed to select maneuvers. This is a simple and efficient maneuvering decision method in one-on-one engagement. On this basis， Baris and Emre [5] designed the basic maneuvers library using hybrid automaton， and constructed game matrix，and adopted the minimax game to solve the mixed strategy to obtain the optimal maneuver. The maneuvering decision method is verified in one-on-one engagement. Nelson and Rafal [6]presented a real-time autonomous decision making approach combining discretized guidance-law and game theory;similarly， it used the minimax search algorithm to select optimal maneuver and the validity of this method is verified.Virtanenet al. [7] proposed an influence diagram method to obtain the optimal flight paths accounting for given air combat maneuvers， which is an off-line method with a large amount of calculation. McGrewet al. [8] presented a maneuvering decision strategy called approximate dynamic programming for rapidly changing tactical situations， it can provide a fast response， and the flight results have successfully shown in MIT’s indoor autonomous vehicle test environment. Srivastava and Surana [9] explored Monte Carlo tree search (MCTS)for tactic maneuvering decision between two UCAVs， which employed self-play to select the optimal maneuver against adversary tactics. Bertram and Wei [10] applied Markov decision processes (MDP) to the pursuit-evasion game. The algorithm with online processing ability can be scaled to large team sizes up to 100 vs 100. The effectiveness of algorithm is verified in the 3D visualization simulation environment developed by themselves.

In terms of data-driven methods， these kinds of methods have developed rapidly in recent years. Genetic fuzzy trees(GFT) is a novel application in air combat， which was proposed by Ernestet al. [11]， [12]， where an artificial intelligence (AI) system called ALPHA is constructed using GFT. This technology combines several fuzzy inference systems (FIS) with genetic fuzzy tree for air combat decisionmaking. With this approach， the overall complex process of air combat decision-making is divided into multiple FIS， and each FIS can be trained separately. In June 2016， the ALPHA intelligent air combat system (to control four unmanned aerial vehicles (UAVs)) developed by the USA successfully defended the coastline without loss by defeating two jet fighters operated by retired fighter pilots in air combat simulation.However， GFT is only a temporary algorithm and has not been widely used and promoted. In August 2020， in the final of the ALPHA dogfight trials held by defense advanced projects research agency (DARPA)， Heron Systems won the championship. The AI algorithm they developed defeated a human pilot controlling a virtual F-16 fighter by 5:0 overwhelming victory， but the specific technologies have not been reported. It is understood that they use an AI algorithm based on reinforcement learning， similar to the multi-agent alliance training architecture in the AlphaStar algorithm [13].According to a replay of the test data， the AI of Heron Systems had a relatively simple confrontation strategy， mainly showing horizontal stable hovering maneuver， without obvious tactical maneuver characteristics. In addition， Lockheed Martin achieved a second place finish in the final of the ALPHA dogfight trials; Their approach combined a hierarchical architecture with maximum-entropy reinforcement learning， integrated expert knowledge through reward shaping，and supported modularity of policies [14]. Recently， research on reinforcement learning for air combat has been springing up. Deep reinforcement learning， inverse reinforcement learning and deep deterministic strategy gradients have been applied in autonomous aerial combat maneuver decisionmaking [15]-[17]. Chenet al. [18] designed and developed a set of UAV autonomous maneuver decision man-machine air combat system based on the Q-learning network including an air combat environment simulation subsystem， manned aircraft operation simulation subsystem， and UAV self-learning subsystem. Sunet al. [19] adopted reinforcement learning to air combat， and proposed a novel tactic emergence algorithm named multi-agent hierarchical policy gradient (MAHPG)，which is capable of learning various strategies by adversarial self-play， and is suitable in coping with complex situations.The effectiveness of the algorithm has been verified through air combat simulators. In May 2020， RAND Corporation [20]released a technical report analyzing the feasibility of using AI to assist air combat mission planning. The research team tested several learning techniques and algorithms to train intelligent agents capable of air combat planning in simulated environments. The goal was to harness the capabilities of AI systems to repeat large-scale simulations and obtain continuous improvement， thus accelerating and enriching the development of combat concepts. According to the report， AI task planning tools will have a significant speed advantage over existing manual or automated planning techniques. The method based on data-driven has high requirements for the hardware platform and requires a lot of offline training.Moreover， the acquisition of complete and effective training sets and the online real-time application of training sets are difficult issues.

However， most of the work presented above using the 3-degrees-of-freedom (3-DOF) point-mass aircraft model lack practical utility. Our simulation environment is high fidelity compared with most other works. The flight dynamics model of the F-16 aircraft with 6-degrees-of-freedom (6-DOF) is used as control object. The F-16 aircraft model is considered to be very accurate for modeling aerodynamics， which makes the problem harder undoubtedly. This is also the difficulty and bright spot of this paper. Moreover， in some studies， the aircraft performance of the opponent and ours is set to be different. Usually， the friendly aircraft is given a performance advantage over the opponent aircraft to ensure a higher probability of winning， such as in [8]. In this paper， the performance of both aircraft is identical， which can prove the effectiveness and superiority of the proposed method more objectively and truly. With regards to autonomous maneuver decision algorithms， synthesizing the above analysis， the machine search method was adopted. The creative thinking of this paper is inspired by the game-matrix and game mixed strategy. The game-matrix and minimax search algorithm are practical and effective approaches， but the maneuver library need to be designed in a different way. Additionally， the usual minimax game algorithm is for pure strategy， which is deterministic and not quite appropriate to dynamic combat situations. The mixed strategy is a good solution， but determining how to obtain the optimal mixed strategy is worth researching.Respecting this problem， this paper proposes a novel optimization algorithm named transfer learning pigeon-inspired optimization (TLPIO)， and applies it to determine the mixed strategy， and then the optimal maneuver can be obtained.

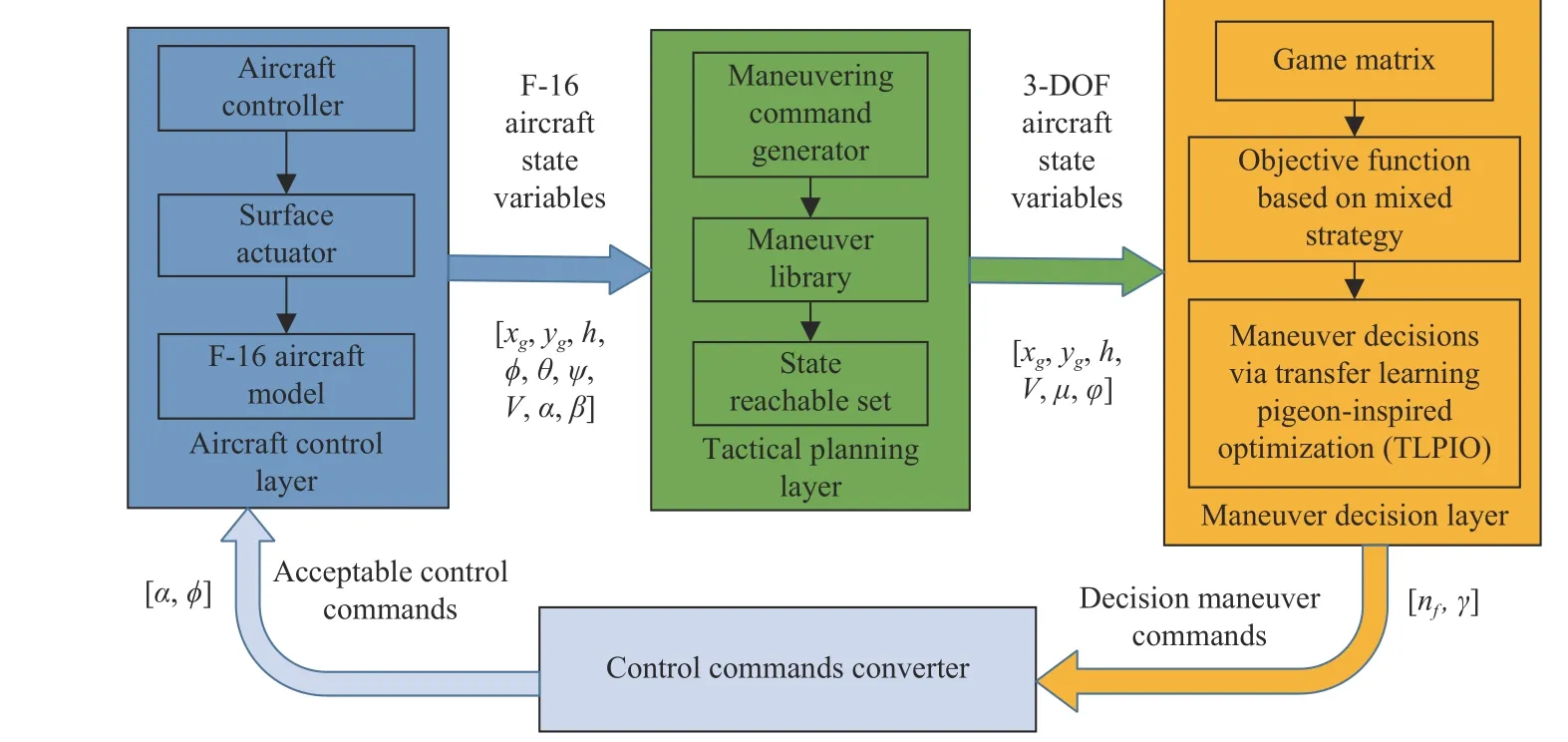
Fig. 1. The air combat system architecture of autonomous maneuver decisions via TLPIO.

Pigeon-inspired optimization (PIO) is an efficient swarm intelligence optimization algorithm proposed by Duan and Qiao [21]， which is widely used in various fields possessing well exploitation and exploration abilities [22]-[25]. However， there are few applications of the optimization algorithm to autonomous maneuvering decisions in air combat. Besides，the accuracy of the solution is very important in air combat，and the basic PIO easily falls into a local optimum. Transfer learning is a learning mechanism that uses the information obtained when solving historical related tasks to help solve new problems [26]. Inspired by it， the transfer learning mechanism is used to guide population initialization， which can significantly improve the algorithm performance， thus TLPIO is proposed. In order to show the superiority of TLPIO， several classical swarm intelligence optimization algorithms， including PIO， particle swarm optimization (PSO)and genetic algorithm (GA)， are compared with TLPIO， and the results are satisfying.

In summary， the major contributions of this paper are threefold， elaborated as follows.

1) In the aircraft control layer， we construct a flight dynamics model of the F-16 aircraft with 6-DOF with aerodynamic data to simulate the dynamics of real aircraft with the MATLAB/Simulink simulation platform. Based on the aircraft trim， the aircraft ardupilot system is designed.

2) In the tactical planning layer， the 3-DOF aircraft model is used as the maneuvering command generator to derive the control commands of the maneuver library. Then， the expanded elemental maneuver library is designed with normal load factor and bank angle as control commands. Afterwards， the state reachable set can be obtained to prepare for maneuver decisions. In addition， since the control commands of the underlying aircraft controller differ from those of the maneuver library， the control commands converting method is given.

3) In the autonomous maneuver decision layer， which is the UCAV’s brain in aerial combat， the main contributions and focus of this paper are committed. The air combat situation assessment function is designed by simple and effective orientation and range threats. Considering predicting the enemy’s mixed strategy， the mixed strategy objective function of maneuvering decisions is constructed based on the game matrix. The principle of TLPIO and the maneuver decisionmaking process via TLPIO are specialized. The convergence and time complexity of TLPIO are analyzed.

The rest of the paper is organized as follows. The air combat system architecture of the autonomous maneuver decision via TLPIO is described in Section II. Section III describes the F-16 aircraft model and its trim process as well as the control techniques. Section IV presents the maneuvering command generator and expanded maneuver library. In Section V， the autonomous maneuver decision method via TLPIO is proposed. The aerial combat situation evaluation function， mixed strategy game and the principle and convergence of TLPIO are also introduced in this section. Section VI demonstrates simulation results for comparison of different optimization algorithms and different combat scenes. The conclusions are summarized in Section VII.

II. AIR COMBAT SYSTEM ARCHITECTURE

Taking the F-16 aircraft model as the control object， a complete set of one-to-one air combat system consisting of aircraft control layer， tactical planning layer， and autonomous maneuver decision layer is designed. The overview of the air combat system architecture is given in Fig. 1.

The aircraft control layer including underlying controller and surface actuator is used to finish the flight control task.The real F-16 aircraft model takes the pilot’s manipulation as input (throttle， elevator， aileron and rudder). For the UCAV，the underlying controller needs to be designed with autonomous control commands (attack angle and roll angle) as inputs and the throttle， elevator deflection， aileron deflection and rudder deflection as outputs， so as to realize unmanned autonomous control of the aircraft.

The tactical planning layer mainly consists of the maneuver library and maneuvering command generator， serving as a connector between the aircraft control layer and maneuver decision layer. In the tactical planning layer， the F-16 aircraft state variables generated by the control layer (position， roll angle， pitch angle， yaw angle， velocity， angle of attack， angle of sideslip) are converted to 3-DOF aircraft state variables(position， velocity， flight path angle， heading angle). Based on the maneuvering command generator， the maneuver library is designed with normal load factor and bank angle as control commands. Given the maneuver library， all alternative states，i.e. the state reachable set， can be obtained. Then， the state reachable set is input into the maneuver decision layer.

The maneuver decision layer， aiming to generate maneuver commands autonomously according to the confrontation situation， is the core of the air combat system and the focus in this paper. With the state reachable set of both adversarial aircraft， the game matrix can be calculated using the situation evaluation function. Given the game matrix， the maneuver decision objective function can be designed based on the mixed strategy. The TLPIO is used to optimize the objective function to obtain the decision maneuver control commands(normal load factor and bank angle).

The decision maneuver commands (normal load factor and bank angle) are converted into the control commands (attack angle and roll angle) accepted by the aircraft control layer through the control commands converter.

III. AIRCRAFT CONTROL LAYER

A flight dynamics model of the F-16 aircraft， aircraft trim，and control technique are presented in this section.

A. Aircraft Dynamics

The nonlinear 6-DOF aircraft model of F-16 aircraft， a highfidelity flight dynamics model， is the control object in this paper. The aerodynamic coefficients and geometric data derive from the report named Nonlinear F-16 Model Description [27]， nonlinear F-16 model is described by the following equations:

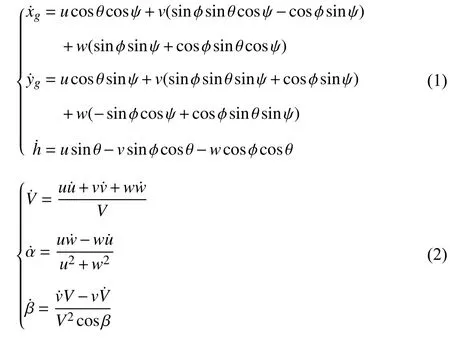
B. Aircraft Trim

The kinematics equation of the aircraft mentioned above is a set of complex nonlinear differential equations. Before analyzing the stability and reliability of aircraft and designing the controller， the aircraft trim should be performed. The socalled trim is set so that the aircraft keeps horizontal steady flight by setting the aircraft’s initial angle of attack and the angle of the elevator deflection to make the resultant force and moment of aircraft equal to be zero， that is， to determine parameters of the aircraft at the equilibrium point. Only based on trim， can the F-16 aircraft model fly stably with a variety of control commands.

Here， the nonlinear simplex method is used to trim the aircraft at different altitude and speed. The steps are as follows:

1) Set the flight parameters， such as the aircraft’s geometric parameters， moment of inertia， aerodynamic coefficient，atmospheric density， gravitational acceleration， etc.

2) Set the initial motion states of the aircraft， including speed， altitude， etc.

3) Establish the trim equations， establish the solution method of the equations， estimate the trim initial values， and calculate the optimization control variables [ α，θ，δT，δe，δa，δr].

4) Take the estimated values and body motion parameters as the initial values， calculate the external forces and moments in the body-fixed reference frame， and then input them into the nonlinear equations， and the new trim value can be obtained by iterative solutions. Determining the convergence according to the accuracy requirements of the optimized control variable. If it converges， then the trim calculation ends; otherwise，the control variables are optimized and the above process is repeated until the result converges.

In this paper， a single point trim is carried out on the F-16 aircraft， with the initial states: altitudeh=3000 m， velocityV=150 m/s， angle of attack α=3.59 deg. The control variables obtained by trim are shown in Table I.

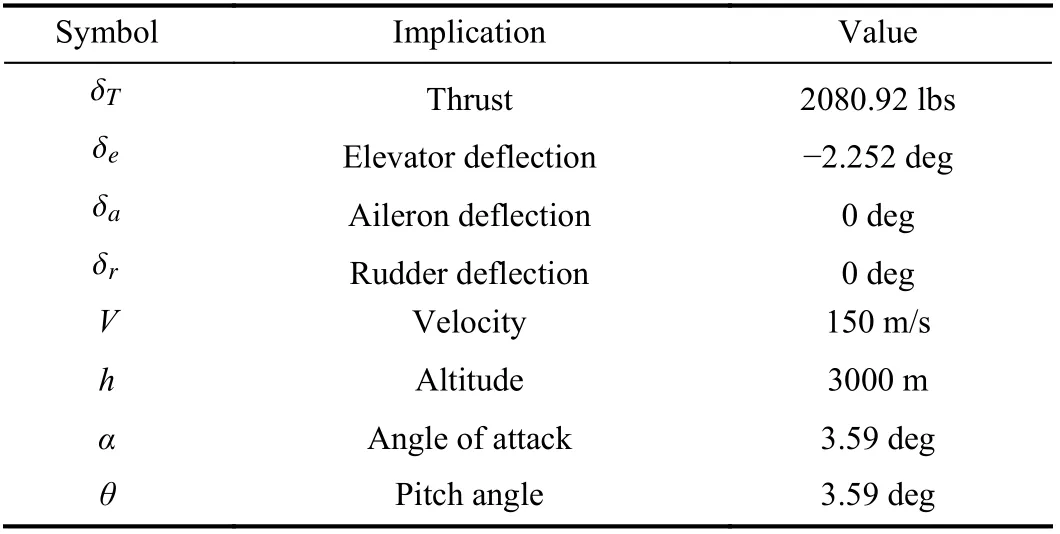
TABLE I CONTROL VARIABLES OBTAINED BY TRIM

C. Control Architecture

A brief description of the control techniques is introduced in this section. The control variables of F-16 aircraft are throttle，elevator deflection， aileron deflection， and rudder deflection.After trimming， the control input of the aircraft is the superposition of the trim values and the expected control commands. The control surface actuator structure diagram built using Simulink is shown in Fig. 2.

In order to make the aircraft stable， the longitudinal and lateral control stability augmentation system need to be designed.

The longitudinal channel refers to pitch angle control through the elevator， where the attack angle autopilot was designed， as shown in Fig. 3(a). The short-period damping of the longitudinal channel is improved by giving the pitch angle rate feedback. In the damping loop， the attack angle attitude control loop is designed， and the stability enhancement control of the longitudinal loop of the control system is realized by feeding back the attack angle information.

In the lateral channel， lateral movement refers to roll and yaw movement， mainly achieved using the through aileron channel and rudder channel. For the aileron channel，considering the feedback of roll angle and roll angle rate， the aileron control stability augmentation system by the roll angle was designed， as shown in Fig. 3(b). For the rudder channel，the feedback of the yaw angle rate and side overload are considered， and at the same time， the effect of aileron and elevator on the rudder is considered. Among them， the yaw angle rate feedback is mainly used to increase the damping of the Dutch roll mode， and the side overload feedback is beneficial in raising the Dutch roll frequency， so that the side overload and sideslip angle can be reduced in the case of roll maneuver and lateral disturbance. Similarly， the roll angle rate and attack angle feedback is aim to improve the damping. The rudder control stability augmentation system is shown in Fig. 3(c).

After completing the design of the above longitudinal and lateral control stability augmentation system， an UCAV ardupilot with the attack angle and roll angle as input control commands is obtained. The inputs of aircraft control layer are attack angle command and roll angle command. The control layer realizes the flight control of the aircraft by tracking the commands of attack angle and roll angle. The structure block diagram of aircraft control layer is shown in Fig. 4.

The tactical planning layer is used to plan how the aircraft will perform maneuvers and provides an alternative set for maneuvering decision layer. The tactical planning layer contains two main parts: Maneuvering command generator and maneuvers library. In this paper， the maneuvering command generator is designed based on the 3-DOF aircraft model and is prepared for the maneuver library and maneuvering decisions. The maneuvers library is an optional set for maneuvering decisions and is the core part of the tactical planning layer. At present， there are two ways to design the maneuver library including typical tactic maneuver library and elemental maneuver library. A typical tactic maneuver library is based on basic fighter maneuvers (BFMs)， with specific maneuvers (e.g.， Immelmann， High Yo-Yo). An elemental maneuver library is based on onboard maneuvers， and the most famous is the seven elemental maneuvers library designed by a NASA scholar [4]. Compared with the typical tactic maneuver library， the elemental maneuver library has the advantages of flexibility and small decision search space，but it requires extreme manipulation， which does not conform to the reality of air combat. Therefore， an improved elemental maneuver library is designed based on the seven elemental maneuvers library.

A. Maneuvering Command Generator

A 3-DOF aircraft model is employed as the maneuvering command generator. The 3-DOF aircraft model that simulates the performance capabilities of real aircraft can describe the aircraft barycenter motion. The state of aircraft can be computed in this way.

The equations of the 3-DOF aircraft model motion are as follows:

IV. TACTICAL PLANNING LAYER

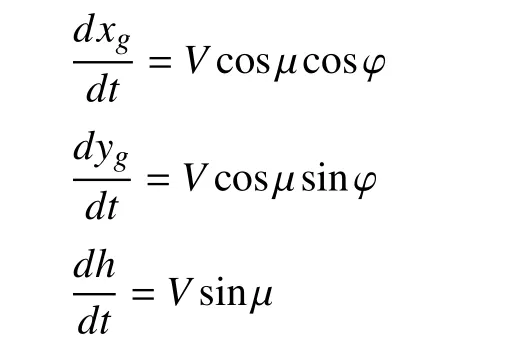
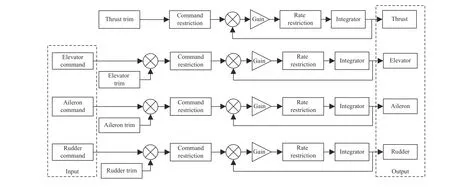
Fig. 2. The surface actuator structure of aircraft.

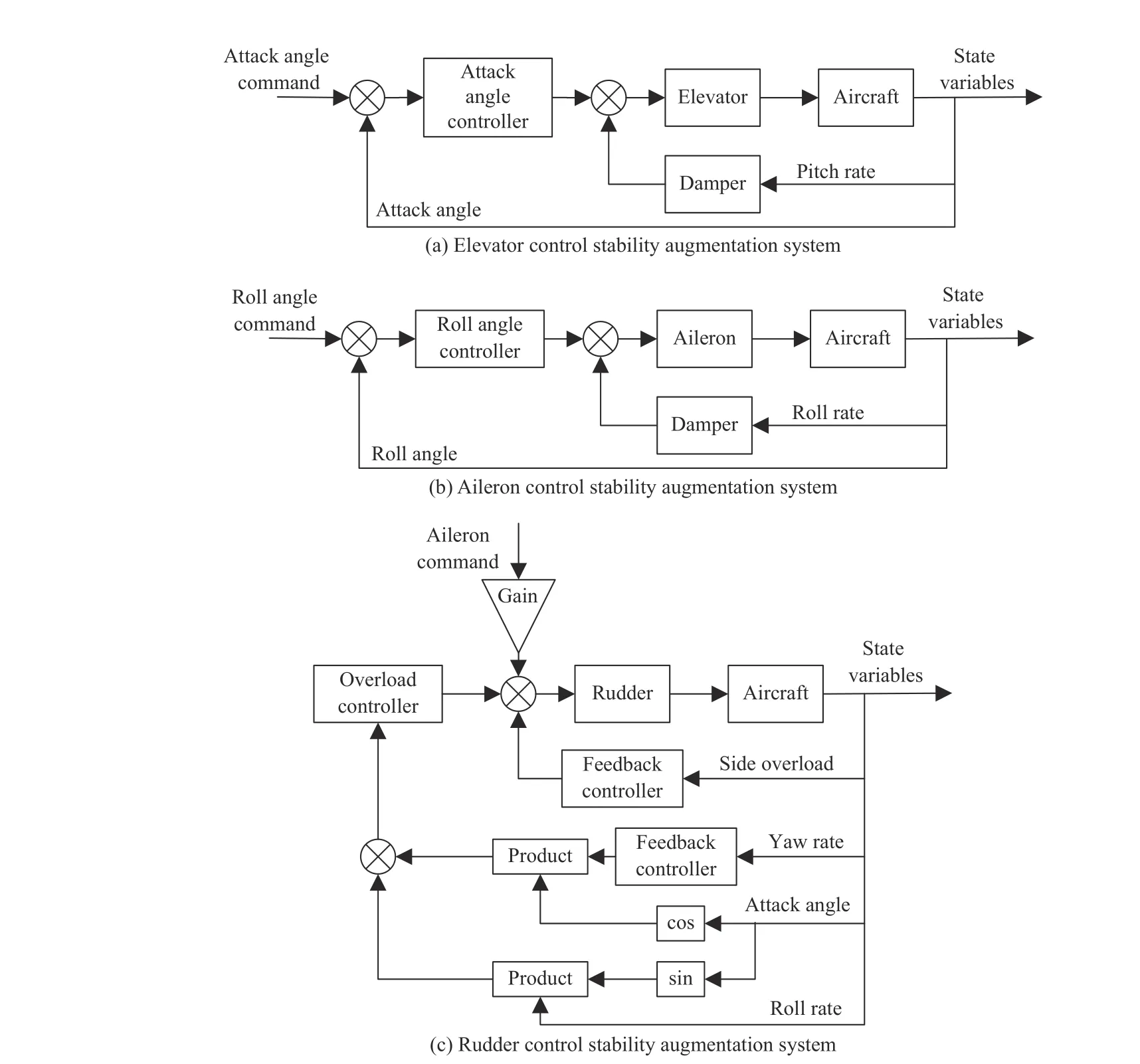
Fig. 3. The control system block diagram of aircraft.

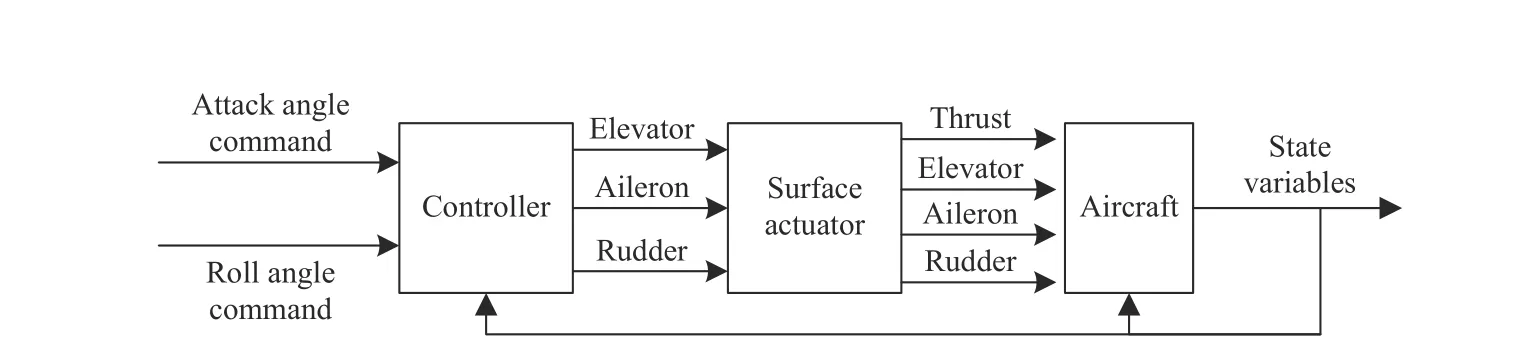
Fig. 4. The structure block diagram of aircraft control layer.

B. Maneuver Library

An maneuver library can be designed based on the maneuvering command generator above. The control variables are the normal load factornf， bank angleγ， and thrust in NASA’s elemental maneuver library， where， thrust can be controlled bynx. Since the control layer takes attack angle and roll angle as control commands，nxis kept unchanged and the maneuver library can be designed withnfandγas control variables.Besides， NASA’s elemental maneuver library involves simple control with maximum control variables， which is impractical for actual air combat. Therefore， an improved maneuvers library was designed， in which the control variable values were set within the feasible domain， so that more maneuvers could be conducted. The expanded elemental maneuvers library is described in Fig. 5.

Fig. 5. The expanded elemental maneuvers.

According to (5)， the requirements of control variable values for elemental maneuvers can be obtained. Based on this， the control algorithm is given in Table II. TheK1，K2canbe set according to the task requirements on the premise of satisfying flight restrictions and safety， in this paper，

TABLE II CONTROL ALGORITHM OF THE EXPANDED ELEMENTAL MANEUVER LIBRARY

K1∈[0，2]，K2∈[-π/4，π/4].

C. Reachable Set of Aircraft States

A reachable set is the set of all states under a specific constraint， and can be divided into forward and backward sets.Forward reachable set: starting from the initial state att0， all control variables in the control constraint set are taken， and the set of all states that can be reached att1. Backward reachable set: the set of all states at timet0that can reach the expected state att1under control constraints. In this paper， we adopt the forward reachable set.

The states reachable set of aircraft is formulated as (6)，shown in Fig. 6.

The states reachable set of aircraft can be obtained according to the following diagram.

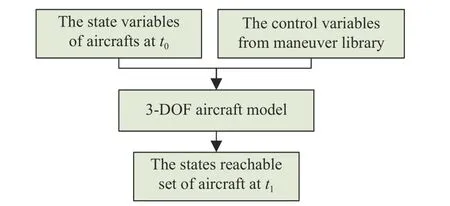
Fig. 6. The states reachable set of aircraft.

D. Control Command Converter

The input commands of the control layer are attack angleαand roll angleφ， and the control commands of maneuver library arenfandγ. Thus， there is a need to convert the commands (nf，γ) into the commands (α，φ). According to the characteristics of the aircraft， there are φ=γ ， and α=knf.Considering engineering practice， the quantitative relationship betweenαandnfcan be approximated， in this paper， i.e.，k=4.

The schematic diagram of control command converter is shown in Fig. 7.

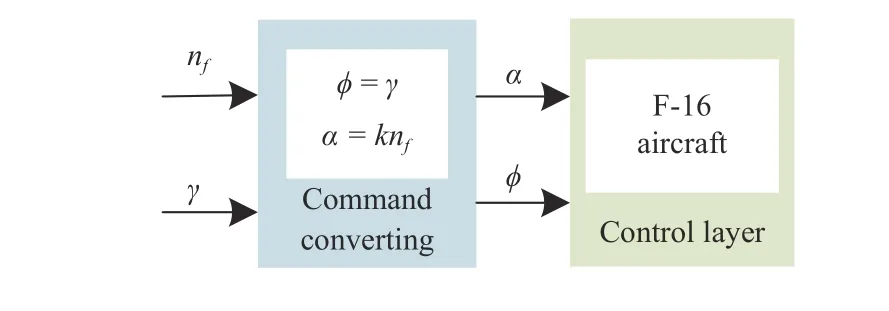
Fig. 7. The schematic diagram of control command converter.

V. AUTONOMOUS MANEUVER DECISION LAYER

The autonomous maneuver decision layer responsible for selecting the optimal maneuver from maneuver library is the core of air combat. The autonomous maneuver decision layer includes situation evaluation and game decision， etc. In this section， aerial combat situation evaluation and game mixed strategy are explained in detail. The specific process of constructing objective function using mixed strategy and implementing TLPIO the will be introduced particularly.

A. Aerial Combat Situation Evaluation

Although there is significant research and improvements on air combat situation assessment functions， the most classic and effective is the influence of orientation and range factors，so this paper also adopts this approach.

The red aircraft is regarded as a friend， and the blue aircraft is an enemy. When evaluating one aircraft’s superiority against the other， the range， friendly aircraft’s bearing angle and enemy aspect angle are used to describe the aircrafts’relationships， represented asM=(D，AR，AB)， whereDis the range， that is the distance between red and blue aircraft，ARis the bearing angle of red aircraft，ABis the aspect angle of blue aircraft.ARandABare positive quantities varying between 0 andπ.

The red and blue aircraft relative geometry is shown in Fig. 8.In air combat， the best position is located at the rear of enemy aircraft with the same heading angle. Thus， the red aircraft would want to minimize theARandAB. The blue would want the opposite. The orientation threat function is described as follows:

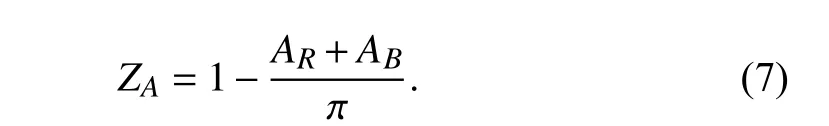
The other part of the evaluation function is the range threat function. The distance between two aircrafts play an important role in the air combat. The relationship between range and superiority is not linear， but approximately a Gaussian distribution， which is related to the missile or gun attack range of two aircraft. When the distance between two aircrafts reaches the optimal attack distance， maximum superiority is reached. The range threat function is as follows:

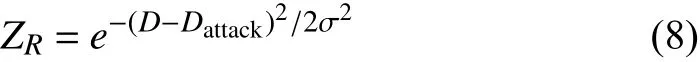
whereDis the distance between red and blue aircraft，Dattackis the mean attack range of red and blue missile or gun.σis the standard deviation， which is equal to 1000 in this paper.

The final situation evaluation function is the product ofZAandZR， presented as follows:

The higher the value ofZZ， the more dominant the red aircraft is; on the contrary， the smaller the value ofZZ， the more dominant the blue aircraft is.

B. Maneuvering Decision Objective Function Based on Mixed Strategy Game

Red and blue aircraft both use the maneuver library described in Section IV-B. Each element in the maneuvers library is a strategy， where the strategy set of red aircraft is denoted asR={r1，r2，...，rm}， the strategy set of blue aircraft is denoted asB={b1，b2，...，bn}.

The states reachable set of aircraft is prepared for maneuvering decisions， and the situation evaluation function is calculated by using the reachable set， after which the game score matrix is obtained.

The game score matrix is denoted asZ， that is， in each step，according to red and blue aircraft states， corresponding to their maneuver libraries， the situation evaluation function of each strategy can be calculated respectively， which constitutes the game score matrix represented as follows:

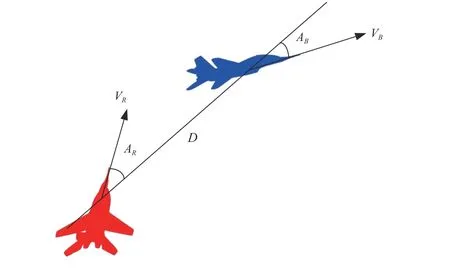
Fig. 8. The red and blue aircraft relative geometry.

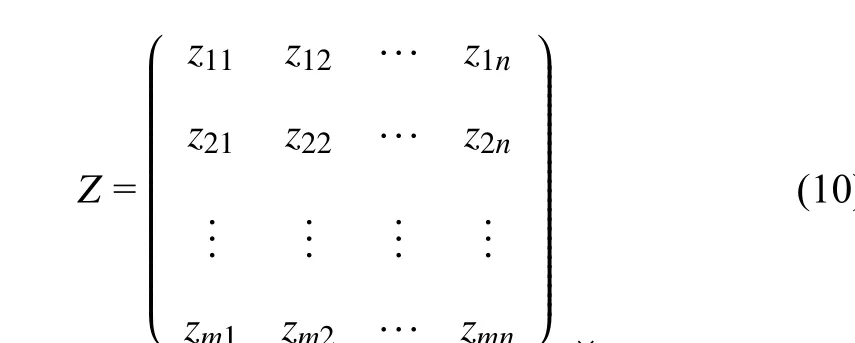
wherezijis the score when the red aircraft selects maneuver strategyriand the blue aircraft selects maneuver strategybj.

In the complete information game， only one specific strategy can be selected with each given piece of information，so this strategy is called a pure strategy. If different strategies are chosen with a certain probability for each given information， it is called a mixed strategy. The mixed strategy is the probability distribution of the pure strategy in space， and the pure strategy is a special case of the mixed strategy.

The traditional minimax algorithm is applied to the matrix game， which adopts a pure strategy， while the mixed strategy is considered in this paper， which is more suitable for complex air combat decision making problems.

The maneuvering decision process is mainly divided into two steps. The first step is to predict the mixed strategy probability of the blue aircraft， and the second step is to calculate the mixed strategy probability of the red aircraft according to the blue’s. The red and blue are a zero-sum game， each trying to maximize its own benefits and minimize the other’s. The detailed decision-making process is as follows.

Firstly， the blue’s mixed strategy of maneuver decision making is predicted according to the minimax principle and the optimization algorithm.

For the mixed strategyQmixof the blue aircraft， the benefit of the red aircraft is represented by formula (11) when it selects rowiof the game score matrixZ. However， the red aircraft would prefer to select a strategy to maximize its benefits represented as (12).

C. Transfer Learning Pigeon-Inspired Optimization

1) Basic Pigeon-Inspired Optimization:Pigeon-inspired optimization (PIO) is a bionic intelligent optimization algorithm which simulates pigeon homing behavior. During the homing process， pigeons initially navigate according to the sun and geomagnetic field， and then use landmarks to navigate when approaching their destination. These two processes are represented as a map and compass operator and landmark operator in mathematical form. The two operators are executed successively， which is the PIO algorithm， where the position of the pigeon is the feasible solution. The aim is to find the optimal solution among all the pigeons.

In the map and compass operator， the iterations areTmax1， att-th iteration， and the velocityVi(t) and positionXi(t) of pigeoniare updated according to the following:

wherefis the objective function to be optimized.

The initial population of the basic PIO is randomly generated in the feasible domain， without considering whether similar problems have been optimized before and whether effective information can be obtained from historical problems to solve current problems， which may affect the search accuracy of the algorithm. If the historical information can be reasonably utilized to generate a more beneficial initial population， the population evolution process can be accelerated.Transfer learning refers to a learning process in which knowledge learned in the old domain is applied to the new domain by using the similarity of data， tasks or models.Inspired by this， the transfer learning mechanism is introduced into PIO and the transfer learning pigeon-inspired optimization (TLPIO) is proposed. Details are covered below.

2) Transfer Learning Pigeon-Inspired Optimization:Transfer learning is an important branch of machine learning， and its essence is to use the experience of historical problems to solve new problems. Transfer learning involves two basic concepts， namely “domain” and “task”. The domain D is the subject of learning and consists of two components: The feature space X and the marginal probability distributionP(Xd)， whereXd={xd1，xd2，...，xdn}∈X，Xdrepresents the data stored in the feature space，xdiis thei-th sample.Domainis divided into the source domain Dsand target domain Dt.As the name implies， the source domain corresponds to historical problems， while the target domain corresponds to problems to be solved. The task T is the object of learning and consists of the label space Y and its corresponding functionf(·).

Definition 1 (Transfer Learning) [28]:Given the source domain Dsand source task Ts， the target domain Dtand target task Tt， the aim of transfer learning is to promote the target learning functionft(·) in Dtusing the knowledge inDsand Ts， where Ds≠Dt， or Ts≠Tt.

The followings are the explanations applied to PIO for the three problems of transfer learning: what to transfer， how to transfer and when to transfer.

“What to transfer” is the core problem of transfer learning，which aims to find the similarity between the source domain and target domain and make reasonable use of it to realize effective transfer of knowledge. In this paper， Kullback-Leibler divergence (KL divergence) is adopted to measure the similarity， as defined below.

Definition 2 (Kullback-Leibler Divergence):BothP(x) andQ(x)are the probability distributions on random variableX，the KL divergence is represented as follows:

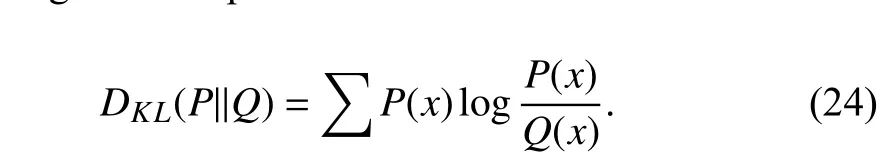
KL divergence can be used to measure the similarity between two probability distributions. The more similar the two probability distributions are， the smaller the KL divergence is. For TLPIO，P(x) represents the probability distributions of the problem to be optimized， andQ(x) represents the probability distributions of problems have been optimized.“What to transfer” is regarded as the transfer evaluation criterion， and “How to transfer” is the transfer method， they are complementary and closely related.

“How to transfer” refers to the learning algorithm. For TLPIO， the target domain can be obtained by executing the map and compass operator forTtdtimes. The historical solutions are regarded as the source domain. The number of transferring populations is calculated as follows:

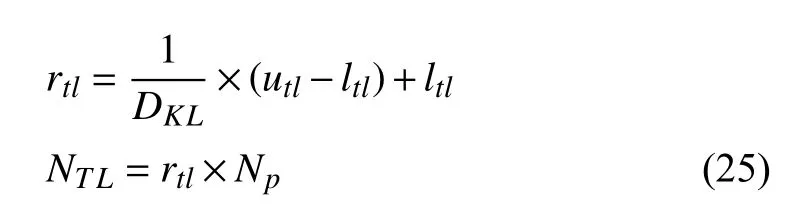
wherertlis the proportion of the transferring population，DKLis the KL divergence，utlandltlare the proportional upper limit and proportional lower limit respectively， whereutl=0.4，ltl=0.1 in this paper.Npis the number of the initialized population，NTLis the number of the transferring population.Note， ifrtl＞1， thenrtl=1.

After determining the number of the transferring population，arrange fitness values ofsource domainin descending order，and take the firstNTLas the transferring source.

“When to transfer” points out the transfer learning condition. If there is no or weak similarity between the two domains， then transfer learning will have a negative effect on the solution， which is called a “negative transfer”， so the conditions on “when to transfer” should be given. In this paper， we stipulate that transfer learning is performed whenDKL≤1.

The procedure of the proposed TLPIO algorithm is presented in Algorithm 1.

Algorithm 1 TLPIO Algorithm Input: The objective function， source domain.Output: The best solution.1: Initialize parameters.2: For i = 1 to Np do 3: Initialize the velocity and position of each pigeon.4: Calculate fitness of each pigeon and obtain .5: End for/* Form target domain*/6: For t = 1 to Ttd do 7: Update the velocity and position of pigeons by (17) and (18).8: Check whether each velocity and position exceed the boundary value， if so set it to the boundary value.Xgbest 9: Calculate fitness of each pigeon and update .10: End for 11: The updated position and fitness of each pigeon are used as the target domain/* Transfer learning*/12: Calculate KL divergence by (24).DKL ≤1 Xgbest 13: If ， do Step 14， else do Step 16， end if.14: Calculate the number of transferring pigeons NTL by (25).15: Arrange fitness values of source domain in descending order keeping unchanged， and the first NTL are selected as transferring source to replace NTL pigeons of initialized population./* Map and compass operator*/16: For t = 1 to Tmax1 do 17: Update the velocity and position of pigeons by (17) and (18).18: Check whether each velocity and position exceed the boundary value， if so set it to the boundary value.Xgbest 19: Calculate fitness of each pigeon and update .20: End For/* Landmark operator*/21: For t = 1 to Tmax2 do 22: Update the velocity and position of pigeons by (19) and (23).23: Check whether each velocity and position exceed the boundary value， if so set it to the boundary value.Xgbest 24: Calculate fitness of each pigeon and update .25: End For Xgbest

3) Convergence and Time Complexity Analysis of TLPIO:Since the initial population has no effect on convergence， the mathematical proof of convergence of TLPIO is consistent with that of PIO. TLPIO can converge to the global optimum，and the convergence analysis is given below [29].

Definition 3 (Markov Chain):A stochastic process is defined as a collection of random variables. The possible values of random variables form a setScalled the state space. If a sequence of discrete random variables {ξk，k≥0} satisfy the Markov property， namely that the probability of moving to the next state depends only on the present state and not on the previous states

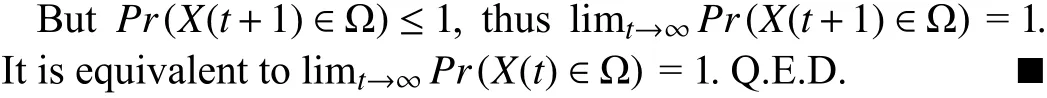
The time complexity is commonly expressed using big O notation. The population size of pigeons isNp， the dimension of each pigeon isDdim， the computational cost of objective function isCf. the iteration isTmax. The time complexity of the map and compass operator is O(Np(Ddim+Cf)). The time complexity of the landmark operator is O(NplogNp+Ddimlog×Np+CflogNp). There is a transfer process in TLPIO， in which the time complexity of the formation of the target domain is O(TtdNp(Ddim+Cf))， and time complexity of the remaining steps can be omitted. The total time complexity is O(Tmax(Np(Ddim+Cf)+NplogNp)+TtdNp(Ddim+Cf)).

D. Implementation of TLPIO for Autonomous Maneuver Decisions

For the aforementioned maneuvering decisions problem， the pigeon’s position is the mixed strategy probabilities tuple. The formula (13) is regarded as the objective function optimized by PIO， and the best mixed strategyQmix*of the blue aircraft can be obtained. It serves as the predicted the blue aircraft mixed strategy to construct the decision function of red aircraft. The formula (15) is taken as the objective function and TLPIO is used to solve the best mixed strategyPmix*of the red aircraft. Note， both of these two optimization problems are constrained， and we can turn them into unconstrained optimization problems with a little trick to accommodate the PIO/TLPIO. We set the pigeons’ positions with the range[0， 1]， in order to ensure that the sum of all dimensions is 1，and take the normalized value.

The air combat terminates when an aircraft shoots down the other or the predefined simulation time ends. Moreover， the attack weapon carried by the aircraft needs to be modeled.The weapon attack area is regarded as a cone in which theXaxis of the aircraft body is taken as the central axis and the weapon attack distance is taken as the generatrix. The central angle is 20 degrees， shown in Fig. 9. Considering the uncertainty of the weapon hit rate， the smaller the angle between the line of the target to the attacking aircraft and the line of theXaxis of the aircraft body， the higher the hit rate. In this paper，the hit ratio is set to 0.95 for the central angle within 10 degrees， and 0.9 for the central angle varying from 10 degrees to 20 degrees. When the aircraft meets the attack distance and attack angle range at the same time， determine if the enemy is hit successfully.

Fig. 9. The virtual weapon attack range of aircraft.

The flowchart of autonomous maneuver decisions via TLPIO is shown in Fig. 10.

VI. SIMULATION VERIFICATION AND ANALYSIS

A. Comparison Analysis of Optimization Algorithm

In order to verify the effectiveness of TLPIO， three standard test functions are used to construct the source domain of transfer learning， and take the modified versions of these three standard test functions as the objective function to be optimized. TLPIO is compared with several classical intelligent optimization algorithms (PIO/PSO/GA) to verify its performance. The parameters configuration of the four algorithms are reported in Table III.

Functions of transfer learning source domain are reported in Table IV， and Objective functions to be optimized are reported in Table V.

Four criterions are adopt to evaluate the algorithm performance [30] as follows.

1)Correct Rate:The correct rate is the ratio of the number of finding the optimal solution to the total number of experiments. When the error between the solution and the real optimal solution reaches 0.001， the optimal solution is considered to be found.

whereEris precision，Gbestvalis the actual optimal solution，andCbestvalis the optimal solution calculated.

The experiments were executed 30 times on each objective function and the averaged results is shown in Table VI. As can be seen from the following data， both PSO and GA have unsatisfactory effects in solving high-dimensional problems，and it is difficult to find the optimal solution. Compared with PIO， TLPIO has higher solving accuracy， and its ability to avoid falling into local optimum is significantly improved. It can be seen that population initialization has an impact on the accuracy of PIO. Although TLPIO has no absolute advantage in running time， its convergence iteration times are improved compared with PIO. The running time is not significantly reduced because it takes time to match between the source and target domains.

B. Air Combat Simulation

In order to verify the effectiveness of the autonomous maneuver decisions via the TLPIO algorithm， three different initial scenarios of dogfight engagement were set for air combat simulation. According to the initial relative position and orientation of two UCAVs， it can be divided into opposite， offensive， and defensive scenarios.

Red and blue UCAVs engage in dogfights， where red one is friendly side， blue one is the opponent. The red and blue aircraft possess the same performance giving no performance advantage to the friend side to ensure fairness and better reflect the effectiveness of the proposed algorithm. Both sides have the same weapons configuration with gun range of 800 m.The maximum velocity is 500 m/s， and the height constraint is[500， 20 000] m.

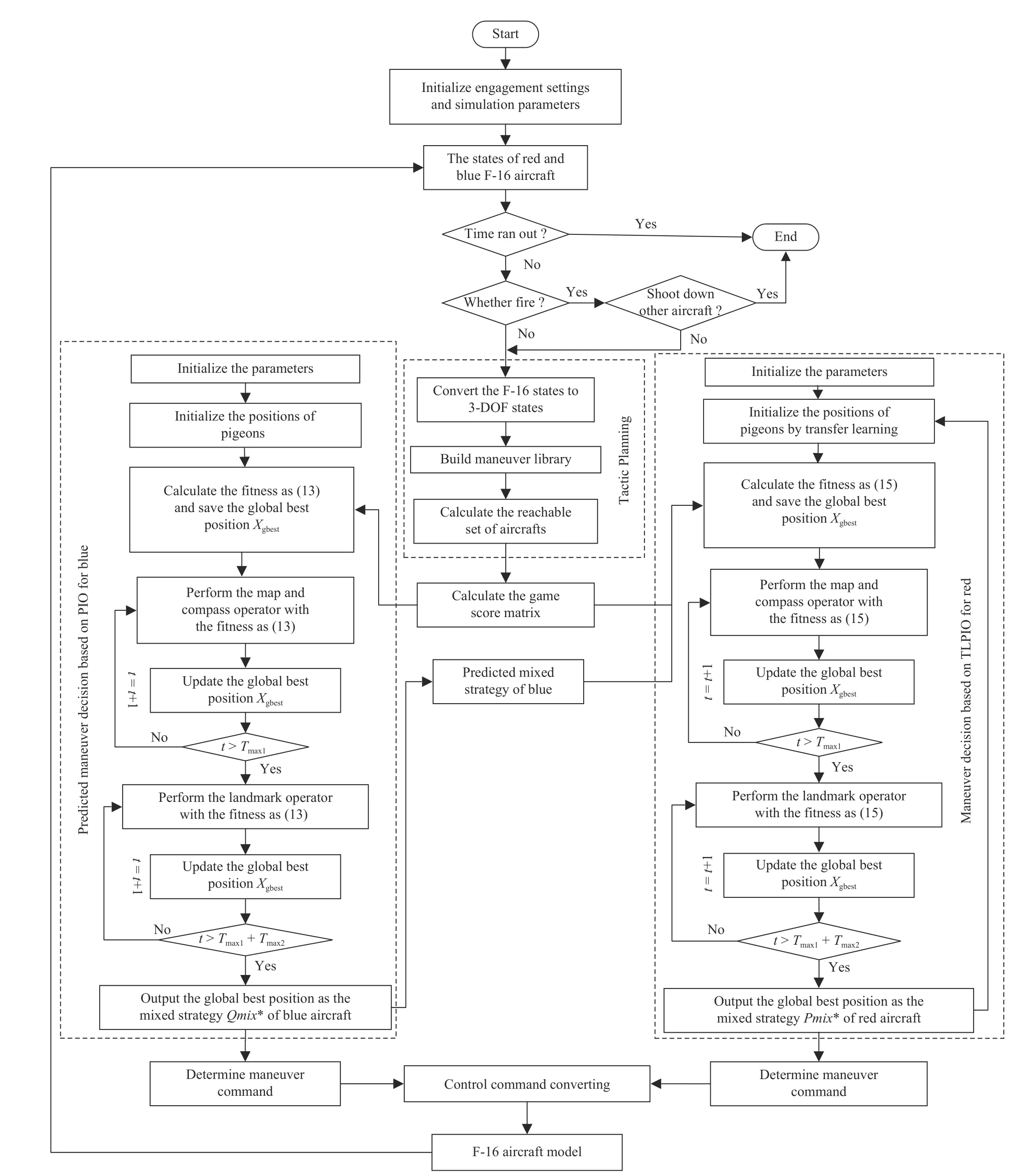
Fig. 10. The flowchart of autonomous maneuver decisions via TLPIO.

Evaluating air combat autonomous maneuver decision performance is not simply a matter of either good or bad performance. The comparisons with other autonomous maneuver decision methods (the minimax game method and stochastic game method) were given to evaluate the proposed method in a more comprehensive manner. Three metrics are chosen to represent success level: the intercept time， the offensive time and the defensive time. The intercept time is defined as the elapsed time required to maintain interception maneuvers until successfully defeating the enemy. The offensive time is measured as the elapsed time required to maintain the offensive situation. The defensive time is measured as the elapsed time required to maintain the defensive situation. These three situation (intercept， offensive， defensive) may not all exist in an engagement simulation. For example， some engagement simulations only have an offensive state and no intercept state.The shorter the interception time， the better， where the interception time is only calculated when the enemy is successfully defeated. The offensive time and defensive time cannot be used to evaluate the performance of an autonomousmaneuver decision method directly， but should be combined with the engagement process and the final outcome.

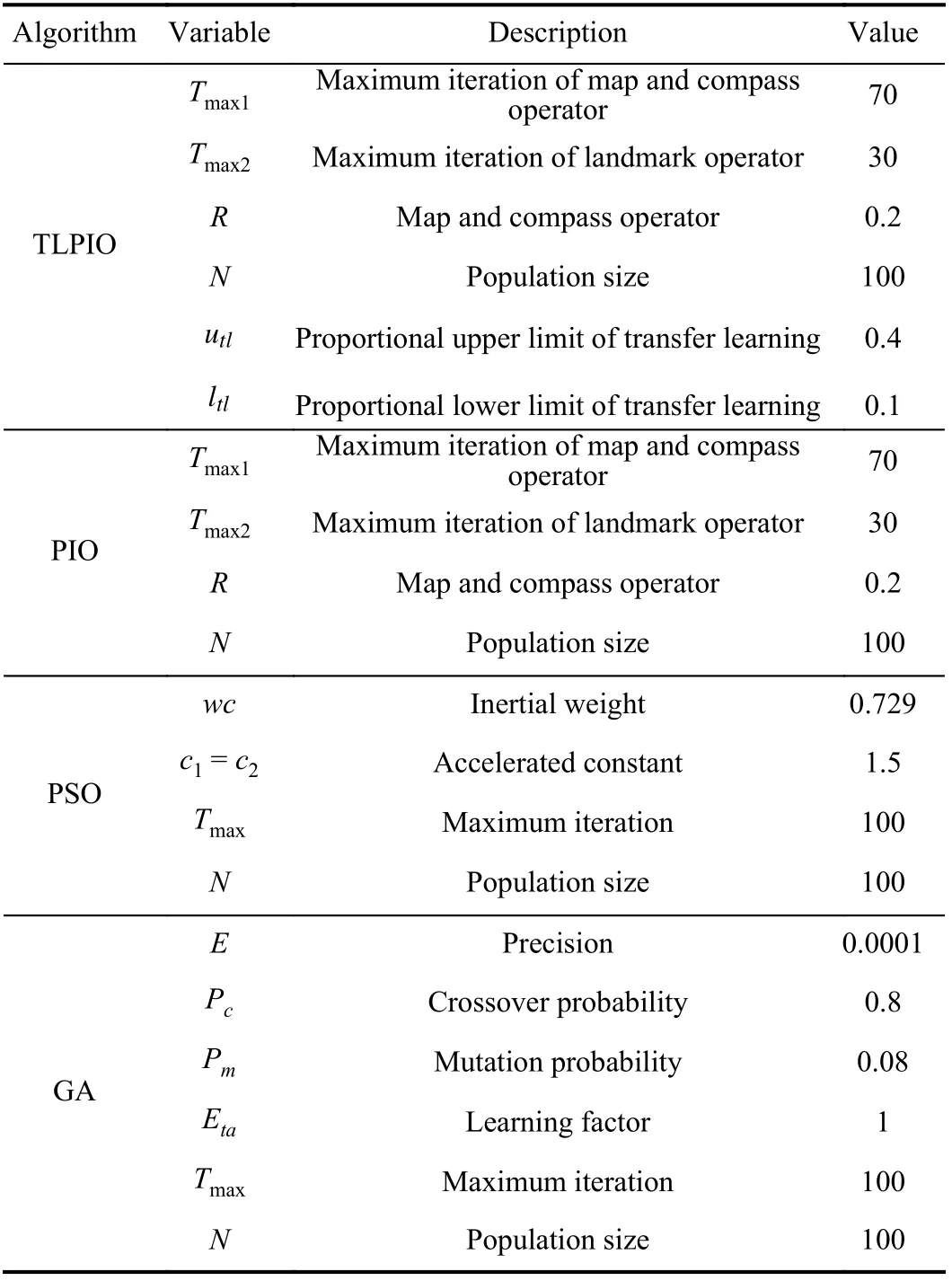
TABLE III PARAMETERS CONFIGURATION OF FOUR ALGORITHMS

TABLE IV FUNCTIONS OF TRANSFER LEARNING SOURCE DOMAIN

TABLE V OBJECTIVE FUNCTIONS TO BE OPTIMIZED

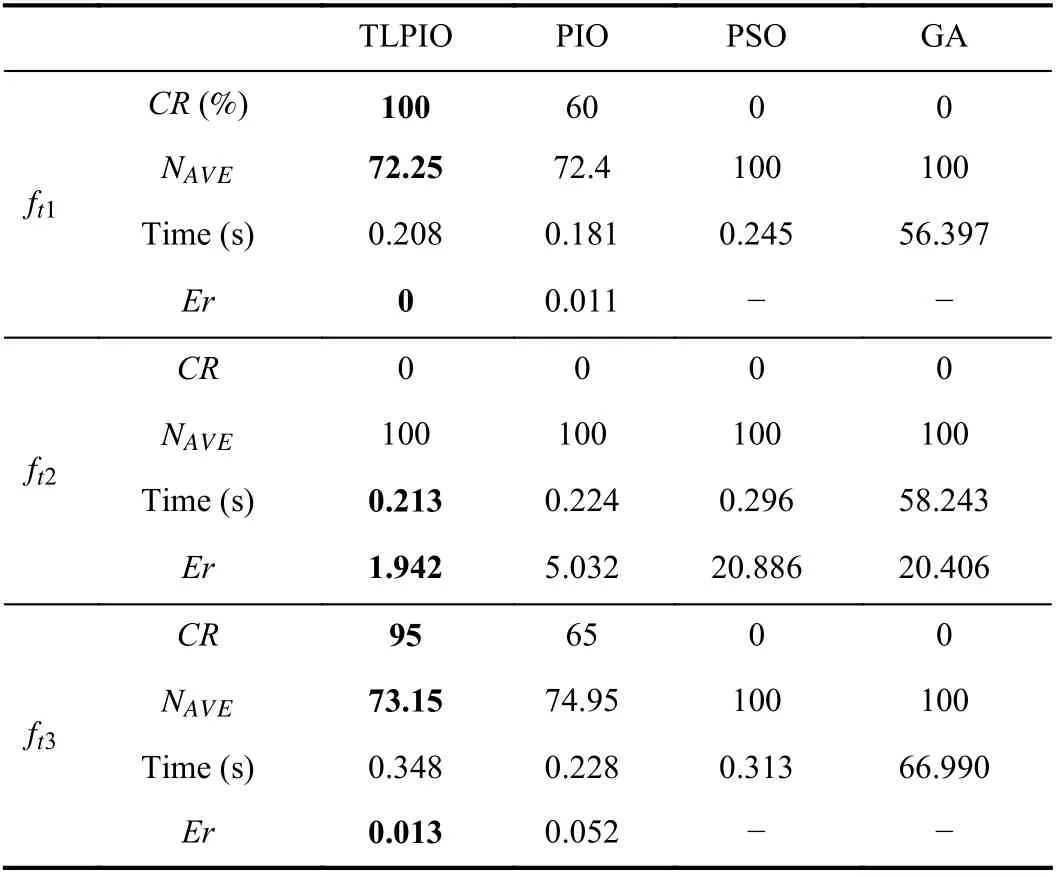
TABLE VI COMPARISON ANALYSIS OF OPTIMIZATION ALGORITHMS

The TLPIO parameters are set as follows: The map and compass factorR= 0.2， the number of pigeonN= 20， the number of iteration for map and compass operatorTmax1= 70，the number of iteration for landmark operatorTmax2= 30， and the proportional upper and lower limit of transfer learning is 0.4 and 0.1， respectively.

The simulation time of air combat is 300 s， and the sampling period of aircraft is 10 ms， and the unit maneuver time is 2 s， so the red and blue UCAV play 150 rounds.

1)Opposite Initial Scenario:The initial scenario setting of air combat is shown in Table VII. At the initial moment， the heading angle of the red UCAV is 15°， while the blue’s heading angle is 180°. Red and blue UCAVs are in a head-tohead position， and the initial flight speed and altitude of both sides are the same. The simulation results are represented in Fig. 11. As can be seen from Fig. 11(a)， from the initial moment， both sides attack the other side， and when the distance between two UCAVs is closer， both sides are in a close chase game with similar directions， and after the last big turn， the friendly UCAV takes the advantage and finally shoots down the opponent in round 122. It is proved that the red’s maneuvering decision based on TLIPO is effective and the predicted blue’s maneuvering is helpful.

TABLE VII THE INITIAL STATES OF TWO UCAVS IN OPPOSITE CASE

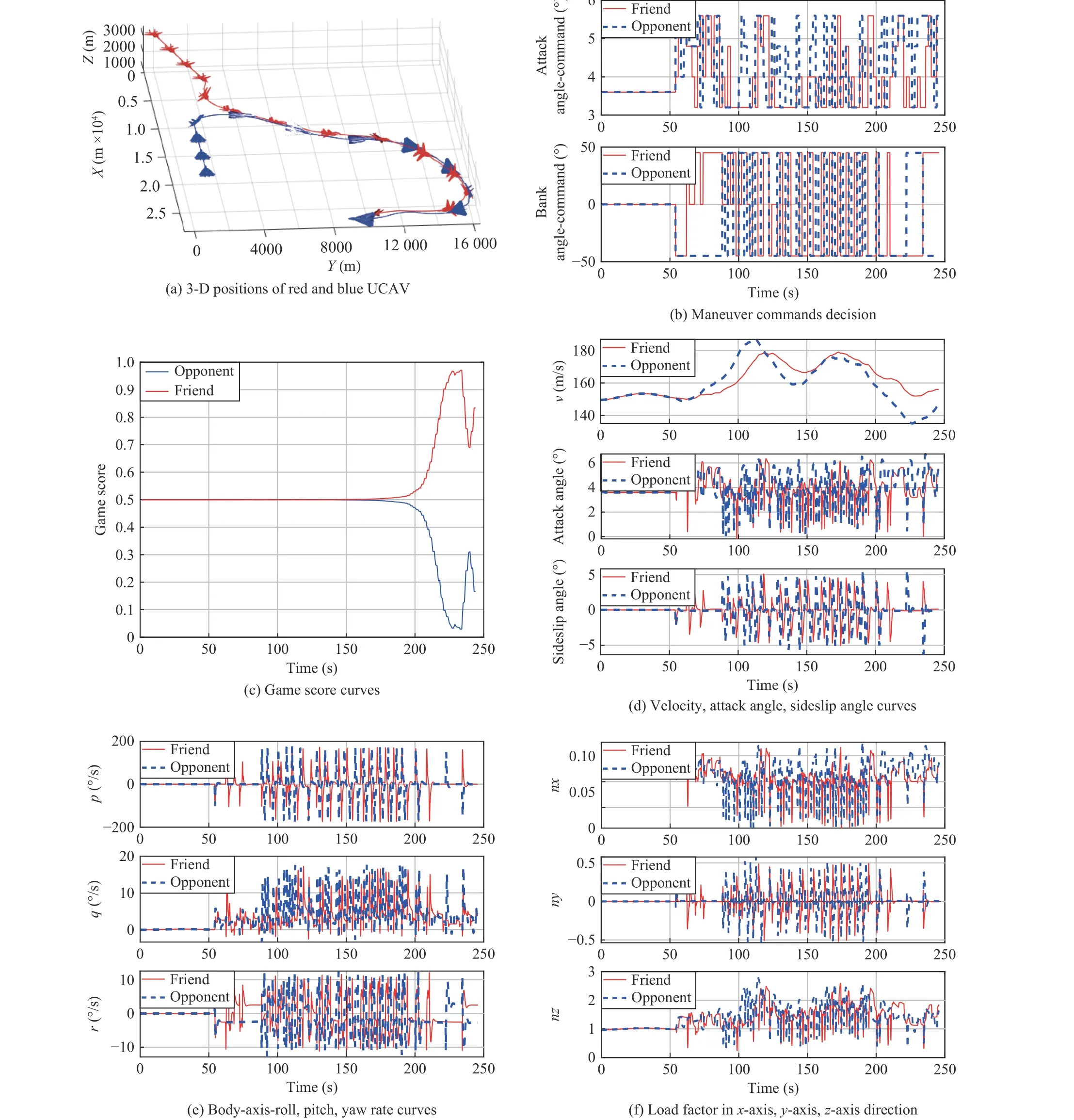
Fig. 11. Simulation results of dogfight engagement in the opposite initial scenario.

Fig. 11(b) shows the maneuver commands selected by both UCAVs at each step， including angle of attack commands and bank angle commands. Both UCAVs frequently change)commands and engage in fierce engagements， and the bank angle commands of both sides become very similar between 100 s and 200 s. This period is in the two sides’ chase game.Fig. 11(c) is the game scores of both sides， namely the situation assessment function values of both sides in each game round. It can be seen that this is a typical zero-sum game， in which the two sides are evenly matched during the first 200 s. After 200 s， the red side gradually overwhelms the blue and finally wins a large number of fights.

The velocity curve， angle of attack curve and sideslip angle curve of both UCAVs are shown in Fig. 11(d). The velocity of both sides fluctuates little， and the trend of increase and decrease is similar. The fluctuations of angle of attack and sideslip of both sides is small， but the change frequency is high. Fig. 11(e) shows the angular rate variation curves of each axis of the two UCAVs. The body-axis roll rate is the largest， followed by body-axis pitch rate， and the body-axis yaw rate， which is the smallest. Fig. 11(f) shows the load factor curves of the two UCAVs. During the first 50 s， all the load factors are almost constant， as the two UCAVs are flying towards each other from a distance during this period. When the two UCAVs get closer， they begin to shift load factors and fight.

In this scenario， the red aircraft uses minimax game method and stochastic game method respectively， the comparison of time performance is shown in Fig. 12. In Fig. 12， only the red aircraft with the proposed method wins， where the red aircraft initiated interception at approximately 250 s and eventually defeated the enemy. The interception time is 17 s， and the offensive time is 194 s. Red aircrafts using the other two methods were always in pursuit and had no intercept time and defensive time. The other two methods have little difference in offensive time and are much larger than the proposed method. It can be seen that the proposed method can win the engagement with greater probability.

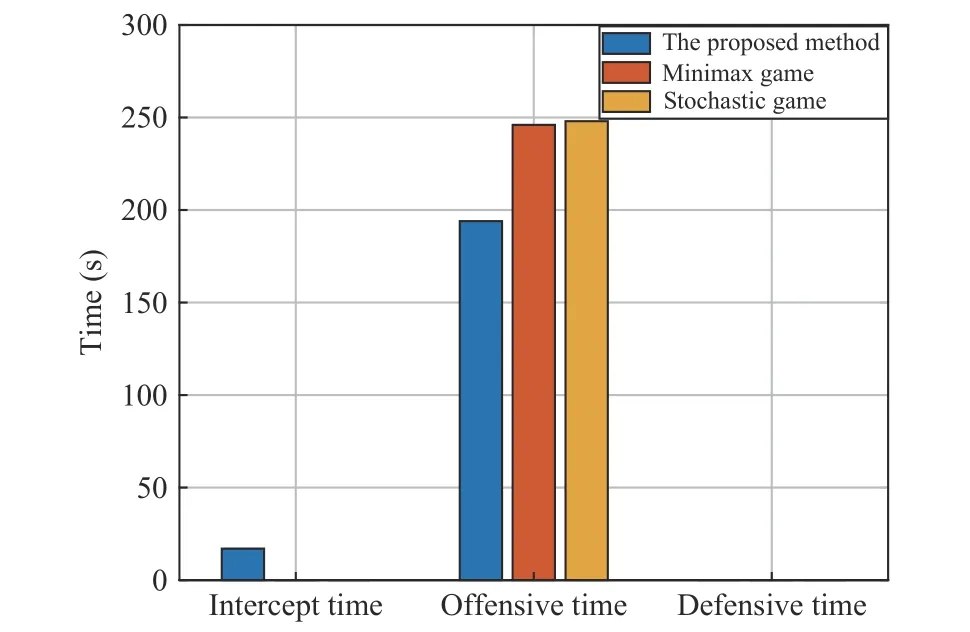
Fig. 12. Comparision analysis of time performanc results of dogfight engagement in the opposite initial scenario.

2) Offensive Initial Scenario:The initial scenario setting of air combat is shown in Table VIII. At the initial moment， the heading angle of the red UCAV is 10°， while the blue’s heading angle is 15°. This means that both sides are flying in a similar direction， and the red UCAV is in an offensive position， which gives us an advantage. The initial flight speed and altitude of both sides are the same. The simulation results are represented in Fig. 13. Fig. 13(a) shows the 3-D positions of two sides during the air combat. At first， although the friendly UCAV has a position advantage， it is not enough to attack the opponent; after a close chase， the friendly UCAV forced the opponent to turn， and then obtained enough advantage， shooting the opponent down in game round 144，which proves the effectiveness of our maneuver decision strategy.

The velocity curve， angle of attack curve and sideslip angle curve of both UCAVs are shown in Fig. 13(b). The velocities of both sides increase and then decrease gradually， and the maximum value is not more than 200 m/s， the minimum value is not less than 100 m/s. The angle of attack and sideslipfluctuate throughout with a small fluctuation range. Fig. 13(c)presents the angular rate variation curves of each axis of the two UCAVs， and Fig. 13(d) shows the load factor curves of the two UCAVs. Since the two sides are in close combat at the beginning， the angular rate and load factor change frequently throughout， and both sides tend to change in approximately the same trend.

TABLE VIII THE INITIAL STATES OF TWO UCAVS IN OFFENSIVE CASE

In this scenario， the red aircraft uses the minimax game method and stochastic game method respectively， and the comparison of time performance is shown in Fig. 14. In Fig. 14，the red aircraft with the proposed method engages in two states: the offensive state first and the intercept state later. The offensive time is 238 s and the intercept time is 30 s. The red aircraft with the minimax game method pursued the blue adversary throughout the engagement， and the offensive time is 298 s. However， the stochastic game method is failure， and there were no offensive maneuvers， defensive maneuvers， and intercept maneuvers， only flying away. Apparently， the proposed method still manages to complete the intercept in less time and with less risk.

3)Defensive Initial Scenario:The initial scenario setting of air combat is shown in Table IX. At the initial moment， the heading angle of the red UCAV is 15°， while the blue’s heading angle is 0°. This means that both sides are flying in similar direction， but the red UCAV is in a defensive position，so the opponent had superiority. The red UCAV has to use a helpful maneuver strategy quickly to evade the attack of enemy. The initial flight speed of both sides are the same. The simulation results are represented in Fig. 15. Fig. 15(a) shows the 3-D positions of the two UCAVs during the air combat.Because the friendly UCAV’s initial position is very dangerous， for a long time， the adversary UCAV chases the friendly UCAV from behind. In combination with Figs. 15(b)-15(d)， it can be seen that the friendly UCAV accelerated quickly and changed its heading angle frequently to avoid the opponent. At around 200 s， the friendly UCAV adopted a serious of effective maneuvers， similar to the Barrel Roll maneuver and continuous High YO-YO maneuver， to break the enemy’s chase advantage. This result is a proof of the validity of the autonomous maneuver decision strategy proposed. The friendly UCAV chose an optimal maneuver decision strategy to avoid the opponent’s air situation superiority and forced the blue adversary to turn around and descend， and finally escaped successfully， drawing even.

In this scenario， the red aircraft uses the minimax game method and stochastic game method respectively， and the comparison of time performance is shown in Fig. 16. In Fig. 16，the red aircrafts using all three methods had only defensive time and all were tied， whereas the defensive time varies among the three methods. The defensive time of the proposed method is shortest， indicting that the aircraft is the earliest out of danger. The minimax game method is second， and the stochastic game method is the worst.

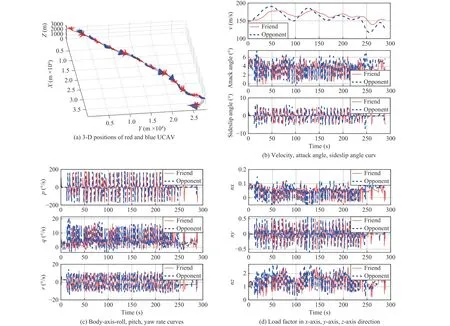
Fig. 13. Simulation results of dogfight engagement in the offensive initial scenario.

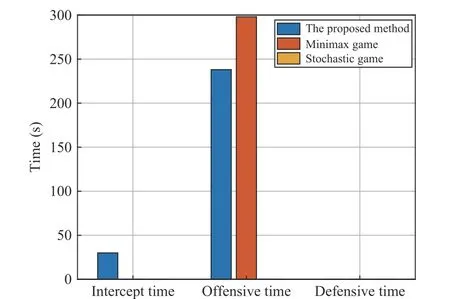
Fig. 14. Comparision analysis of time performanc results of dogfight engagement in the offensive initial scenario.

VII. CONCLUSIONS

This paper presents an autonomous maneuver decisionmethod based on a mixed strategy optimized by TLPIO，which is successfully applied to one-to-one dogfight engagement in a high-fidelity F-16 flight dynamics model.The TLPIO algorithm has good convergence and high accuracy making reasonable maneuver decisions. It is also a beneficial application of a bionic intelligent optimization algorithm combined with transfer learning in air combat decision-making. Given the same aircraft performance， three typical dogfight scenarios simulation results show that when both sides have equal conditions or the friendly side has offensive superiority， the friendly side can consistently defeat the enemy， and when the friendly side has an inferior defensive condition， it can still escape from the enemy’s chase nimbly.

TABLE IX THE INITIAL STATES OF TWO UCAVS IN DEFENSITE CASE

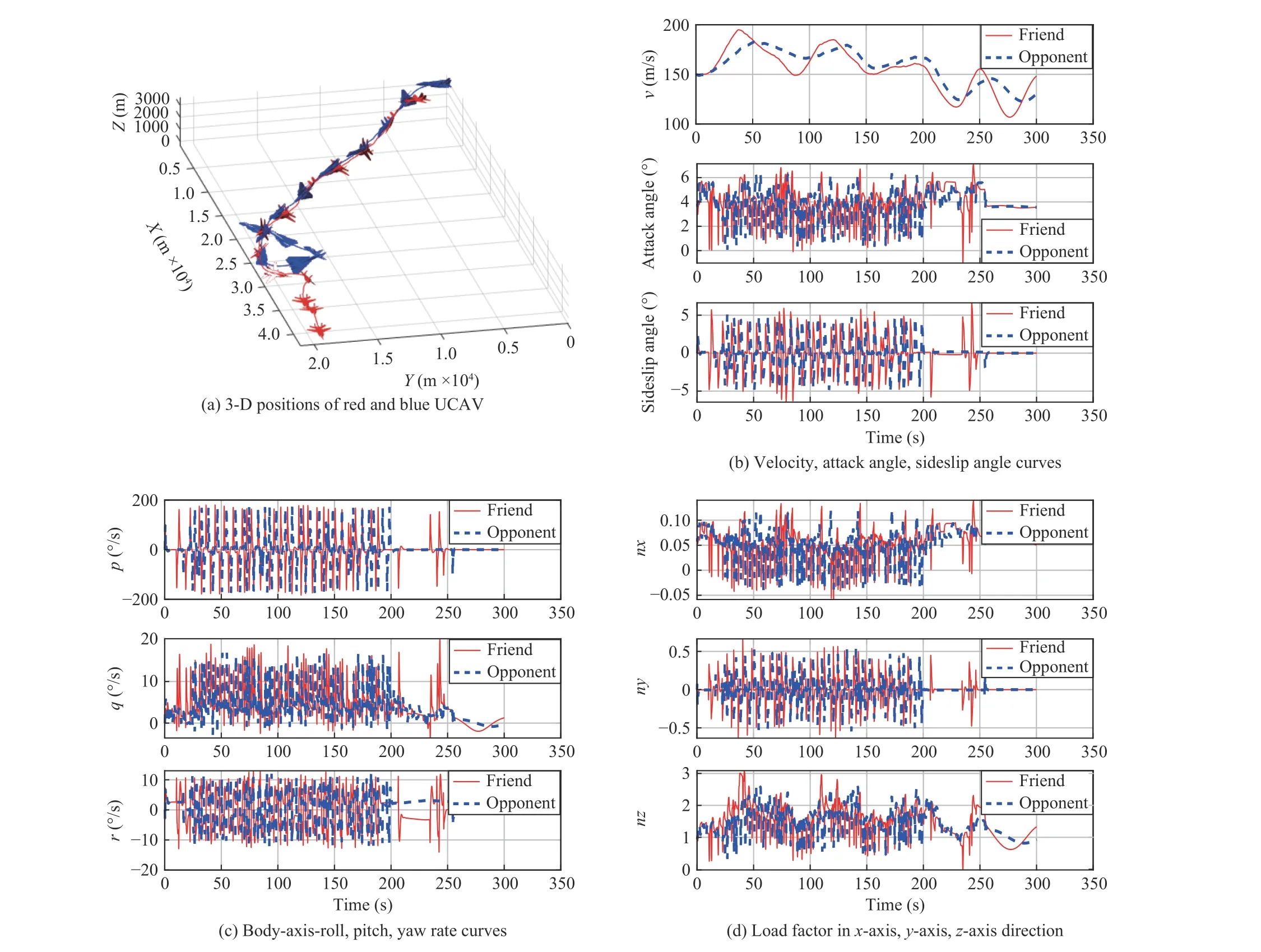
Fig. 15. Simulation results of dogfight engagement in the defensive initial scenario.

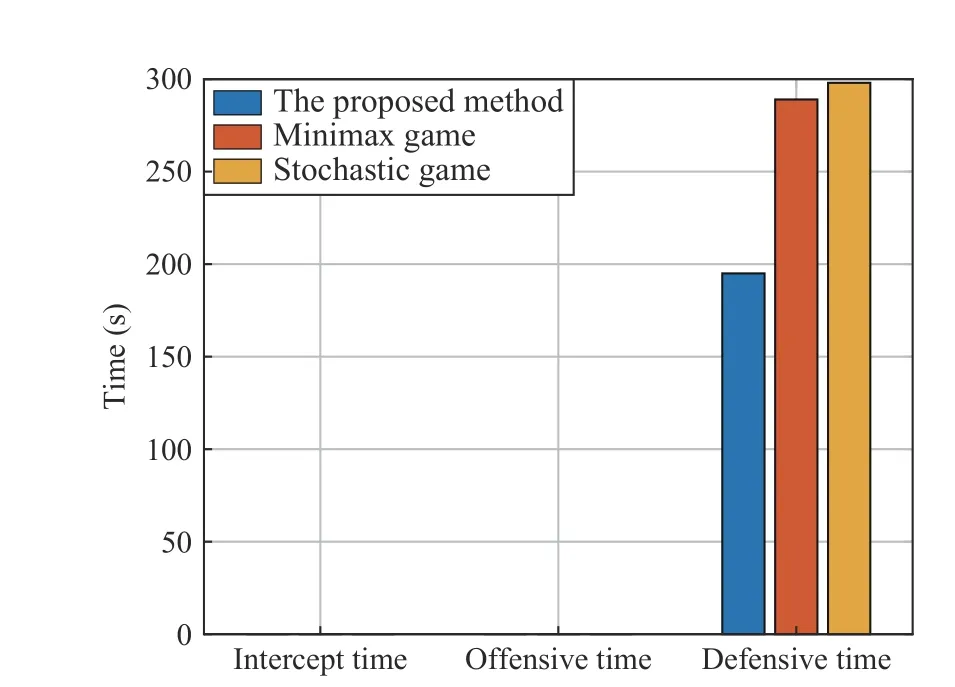
Fig. 16. Comparision analysis of time performanc results of dogfight engagement in the defensive initial scenario.