Reinforcement Learning Behavioral Control for Nonlinear Autonomous System

Zhenyi Zhang，，， Zhibin Mo， Yutao Chen， and Jie Huang，，

Abstract—Behavior-based autonomous systems rely on human intelligence to resolve multi-mission conflicts by designing mission priority rules and nonlinear controllers. In this work， a novel twolayer reinforcement learning behavioral control (RLBC) method is proposed to reduce such dependence by trial-and-error learning. Specifically， in the upper layer， a reinforcement learning mission supervisor (RLMS) is designed to learn the optimal mission priority. Compared with existing mission supervisors， the RLMS improves the dynamic performance of mission priority adjustment by maximizing cumulative rewards and reducing hardware storage demand when using neural networks. In the lower layer， a reinforcement learning controller (RLC) is designed to learn the optimal control policy. Compared with existing behavioral controllers， the RLC reduces the control cost of mission priority adjustment by balancing control performance and consumption. All error signals are proved to be semi-globally uniformly ultimately bounded (SGUUB). Simulation results show that the number of mission priority adjustment and the control cost are significantly reduced compared to some existing mission supervisors and behavioral controllers， respectively.

I. INTRODUCTION

AUTONOMOUS systems have good application potential owing to their scalability and redundancy [1]. The mission execution of autonomous systems is strictly guaranteed by using control theories such as with networked， formation，and containment control [2]， [3]. Nevertheless， these theories rely on human intelligence to design rules directly or indirectly in advance. Data-driven intelligent algorithms reduce or even avoid the dependence on human intelligence through heuristic learning [4]， [5]. Most data-driven algorithms usually lack strict theoretical guarantees such as convergence， stability and robustness. Therefore， scholars are increasingly interested in combining control theories and intelligent algorithms.

An autonomous system has to complete multiple missions together such as moving， obstacle avoidance and following，there will inevitably be conflict. The classical solutions of the multi-mission conflict problem include mission sequencing，mission scheduling and mission prioritization [6]. The mission sequencing method addresses each mission asynchronously，but it is difficult to deal with missions performed synchronously [7]. The mission scheduling method achieves optimal mission allocation， however， it has to consume a lot of online computing resources [8]. The mission prioritization method solves mission conflicts by setting the priority in advance，Nevertheless， it relies on human intelligence or expert knowledge bases [9]. Behavioral control method is the integration of mission scheduling and mission prioritization， which uses a mission supervisor to assign mission priorities [10]-[13].Particularly， the null-space-based behavioral control (NSBC)method completes the highest priority mission and executes a part of low priority missions by using null space projections[14]. However， the priority of the mission supervisor is fixed，which results in the poor dynamic performance of the NSBC method.

To overcome such problems， scholars proposed that the dynamic mission supervisors would include the finite state machine mission supervisor (FSAMS) [15]， the fuzzy mission supervisor (FMS) [16]， [17] and the model predictive control mission supervisor (MPCMS) [18]. The FSAMS first stores the mission priority in some states， then realizes the adjustment by designing the numerical state transition trigger conditions manually. The FMS first needs to design the fuzzy rules and select membership functions. Then， it adjusts the mission priority based on the output of defuzzified.Nevertheless， they depend on human intelligence to design adjustment rules， which is not optimal due to the neglect of future agent states. The MPCMS avoids having to manually design rules by using a switching mode optimal control law and improves optimality by using future forecast information.Since the optimal mission priority must be calculated on-line at each sampling instant， the MPCMS requires a lot of computing resources and storage space. Therefore， One of the motivations of this paper is to design a new mission supervisor to improve the dynamic performance of mission priority adjustment and avoid the on-line calculations，simultaneously.

However， the reference velocity changes significantly or even abruptly when the mission priority is adjusted. Most existing behavioral controllers significantly increase the control quantity to maintain good tracking performance and improve robustness. In [19]， the tracking error of the Euler-Lagrange system achieves finite time convergence by using a nonsingular fast terminal sliding mode adaptive controller(FTSMAC). In [20]， a UAV dynamic controller is proposed to track reference velocity， and the tracking error is asymptotically stable. In [21]， the NSBC method is first extended to the second-order system by designing a second-order nonlinear FTSMAC. In [22]， a fixed-time sliding mode controller is proposed to achieve the fixed-time convergence of tracking error. Since control resources always are limited and the actuators have saturation constraints， excessive consumption is undesirable. The optimal control provides a solution by balancing the control resource and the control performance[23]. However， the strong non-linearity and the inaccuracy of model degrade the control performance of model-based optimization methods. Therefore， the second motivation of this paper is to design a learning based controller to learn the agent model and the control policy， simultaneously.

Motivated by the above discussion， this paper proposes a novel two-layer reinforcement learning behavioral control(RLBC) method for a nonlinear autonomous system. On one hand， the optimal mission priority is learned by designing a reinforcement learning mission supervisor (RLMS). Both the FSAMS and the FMS rely on human intelligence design rules and ignore future state information. However， compared with them， the proposed RLMS avoids designing the rules by trialand-error learning and improves the dynamic performance of priority adjustment by maximizing a cumulative reward. The MPCMS relies on high-performance computing resources and a large amount of storage space to complete the real-time calculation of the optimal mission priority. Nevertheless，compared with the MPCMS， the proposed RLMS shifts the heavy computational burden to the off-line training process，and only stores the network weight after training. In short， the RLMS improves the dynamic performance and reduces the hardware requirements.

On the other hand， the agent model and the optimal tracking control policy are learned by designing a reinforcement learning controller (RLC). Although the lower-layer RLC is designed on the basis of the adaptive dynamic programming(ADP) theory [24]， [25]， there are still the following differences between the proposed RLBC and ADP-based methods. First， the RLBC is an integrated method of decisionmaking and control， in which the NSBC generates a reference trajectory and the RLC tracks such trajectory. Note that the multi-mission conflicts have been resolved at the upper layer.However， ADP-based methods have to use multi-objective optimization to execute multi-mission objectives， which results in complex controller design and difficult stability analysis [26]， [27]. Second， the RLMS may generate a nonoptimal reference trajectory in practical complex environments due to deep neural networks that are unexplainable and the lack of convergence of intelligent algorithms. Once the non-optimal trajectory is given and the control cost increases significantly， the RLC avoids completely tracking the trajectory by minimizing the control cost. In essence， we use the control theory to make up for the lack of interpretation and convergence of the data-driven algorithm.

The specific technological contributions of this paper are summarized as follows:

1) A novel RLMS is proposed to learn the optimal mission priority. Compared with existing mission supervisors， the proposed RLMS avoids artificially designing the mission priority adjustment rules and improves dynamic adjustment performance by trial and error learning. Moreover， the RLMS reduces hardware requirements by shifting the heavy computational burden to the off-line training process.

2) A RLC with an identifier-actor-critic structure is designed to track the reference trajectory optimally. Compared with the existing behavioral controllers， the RLC ensures the robustness and optimality by learning the nonlinear model and the optimal tracking control policy， respectively. In addition，the RLC effectively reduces the control cost of mission priority switching.

3) The tracking error and the network weight error of the identifier， actor and critic all are proved to be semi-globally uniformly ultimately bounded (SGUUB) by using Lyapunov theory. The general paradigm of mission stability with different priorities is given through mathematical induction.Both the mission completion and the control objective achievement are guaranteed theoretically.

The rest of this paper is as follows: In Section II， the preliminaries and problem statement are described. In Section III，a novel RLBC is proposed. Section IV proves the convergence and the stability of controller and mission. In Section V， a numerical simulation is studied. Section VI concludes the paper.

A. Null-Space-Based Behavioral Control

Composite behaviors are the combinations of elementary behaviors with different priorities by using null space projection. The rule design of behavior hierarchy is the same as the MPCMS. The velocity command of composite behavior

II. PRELIMINARIES AND PROBLEM STATEMENT

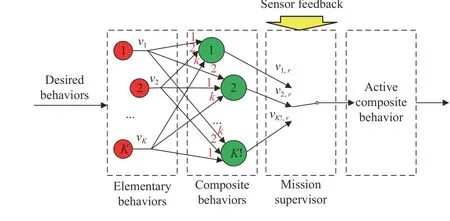
Fig. 1. The structure diagram of NSBC， in which red numbers are the mission priorities [28].

vd(t) is calculated by the following recursive scheme:

B. Modeling

Consider a nonlinear affine system as

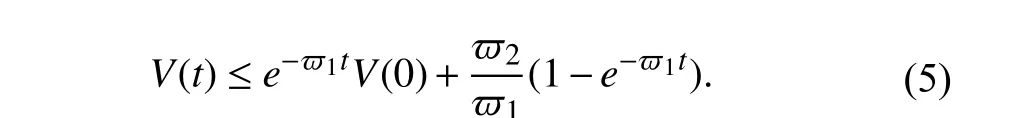
Proof (Lemma 1):The proof is similar to Lemma 1.1 of [36]and is omitted here. ■

C. Control Objective

The control objective is to design a RLBC method for a non-linear autonomous system (4) with Assumption 1 to learn optimal mission priority and reference trajectory tracking control policies in a work environment with Assumption 2，such that i) The mission priority of the agent is switched dynamically and intelligently. ii) The control performance and control resources of agent are balanced， and the tracking error converges to a desired accuracy.

III. REINFORCEMENT LEARNING BEHAVIORAL CONTROL DESIGN

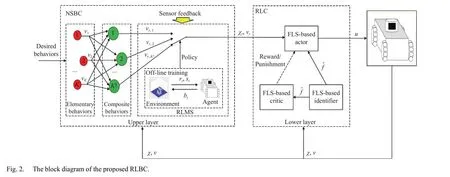
In this section， a novel two-layer RLBC is proposed for a non-linear autonomous system to realize the optimal selection of the mission priority and optimal tracking of the reference trajectory， simultaneously. The block diagram of the proposed RLBC is shown in Fig. 2. In the upper layer， a novel RLMS is skillfully designed by taking the composite behaviors of the NSBC method as the action set of the deep Q network (DQN)algorithm [37]. The prioritized experience replay [38] and the dueling structure [39] are adopted to accelerate network convergence and improve learning efficiency of RLMS，respectively. After off-line training， the learned policy guides the agent to select the mission priority optimally and intelligently. In the lower layer， a RLC with FLS-based identifier-actor-critic architecture is elaborately designed to overcome the difficulty of the analytical solution due to strong non-linearities and achieve the optimal reference trajectory tracking. The FLS-based identifier， actor and critic are developed to estimate the unknown nonlinear term， implement the control input and evaluate control performance，respectively.

A. Reinforcement Learning Mission Supervisor Design

Algorithm 1 RLMS Input: total training episodes ， the time step at the end of a turn， -greedy parameter with decay coefficient .ND Ttotal Te ε γε 1: Initialize replay memory D to capacity Q(s，b;WQ，Wα，Wβ)=V(s;WQ，Wβ)+Ab(s，b;WQ，Wα) WQ Wα Wβ 2: Initialize action-value function with random weights ， ， and .3: For episode = 1; do Ttotal

bt bt=argmaxbQ(st，bt;WQ，Wα，Wβ)9: Sample minibatch of transitions from D with priority;yz=rz+maxbz+1 ˆQ(sz+1，bz+1;W-Q，W-α，W-β)10: ;(yz-Q(sz，bz;WQ，Wα，Wβ))2 WQ Wα Wβ 4: Initialize s0 5: For t = 1; do Te 6: With ε select a random behavior ， otherwise select;bt rt st+1 7: Execute behavior and observe reward and next state;(st，bt，rt，st+1)8: Store transition in D;ND，min (st，bt，rt，st+1)11: Perform a gradient descent step on with respect to the network parameters ， ， ;st+1=st 12: Set ;NC ˆQ=Q 13: Every steps reset 14: End for 15: End for

Remark 2:With reinforcement learning， the grid environment is widely used. Up， down， left， and right are often used as actions. Note that they have no clear physical meaning. In the continuous environment， the velocity and acceleration are often used as actions， but they are artificially defined value ranges. In the RLMS， behaviors are velocity vectors calculated by (1)-(3)， and its physical meaning is the execution of mission. Therefore， the behavior set is different from traditional action set.

B. Reinforcement Learning Controller Design

Theorem 1:Using the RLC defined in (18)， (20) and (22)with the update law (19)， (21) and (23) for the non-linear agent (4) with bounded initial conditions， the design parameters are satisfied with the following conditions:

IV. STABILITY ANALYSIS

whereVuandVηare used to prove Theorem 1 and the stability of composite missions with different priorities， respectively.

Firstly， Theorem 1 is proven for control purposes. The following equation can be deduced by differentiating (26)along (7)， (19)， (21) and (23) as:

V. SIMULATION

In this section， a numerical simulation is given to prove the effectiveness of the proposed RLBC method and its superiority compared to other methods.

A. Case Study

In the simulation case， an autonomous system moves to a target position along a predefined path and avoids the obstacles near the path. The general paradigm of the agent model has been given in (4)， and the simulation uses a numerical case as [43]

The working environment of the agent is two-dimensional，and it has some static and fixed obstacles. The simulation parameters of the environment are listed in Table I.

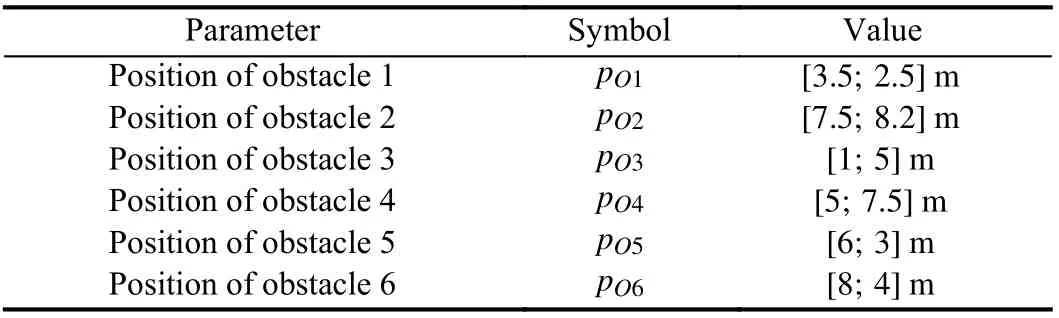
TABLE I PARAMETER VALUES OF THE ENVIRONMENT

The agent has two conflicting missions: motion mission and obstacle avoidance mission. The motion behavior ηMhas the objective of driving the agent to move to a target point along a predetermined trajectory. The mission model and the reference velocity of motion behavior are designed as

Other parameters of the RLMS are listed in Table II.

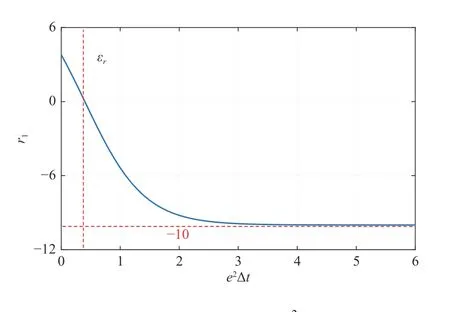
Fig. 3. The pictorial description of the - 10tanh(e2Δt-εr) function.

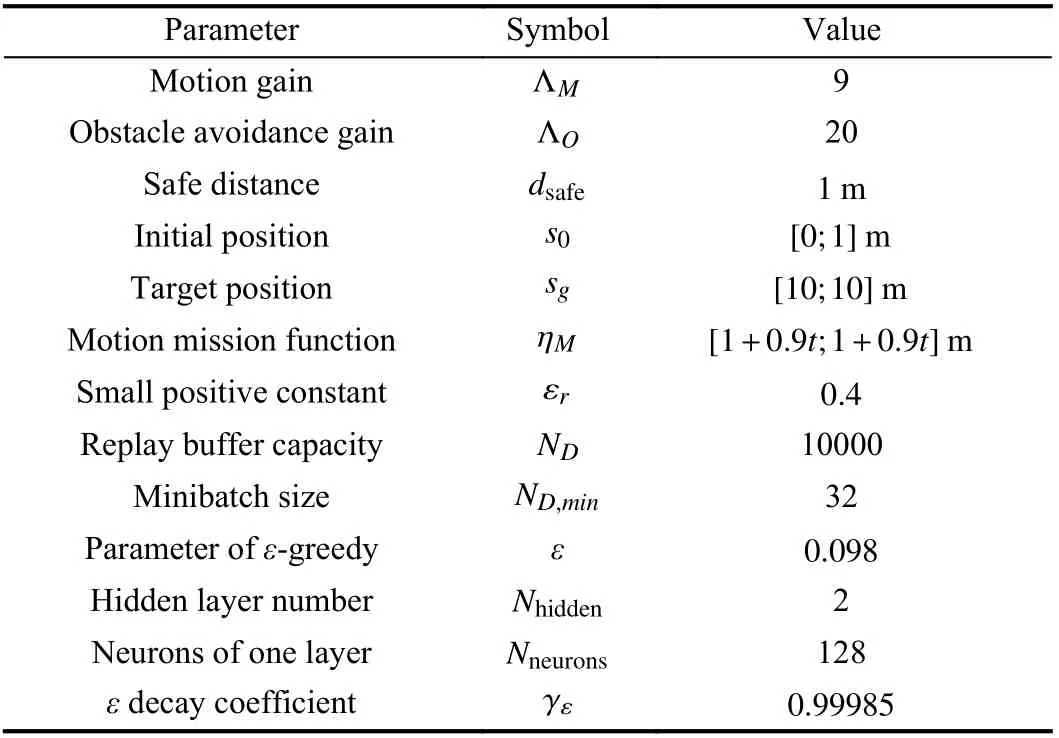
TABLE II PARAMETER VALUES OF THE RLMS

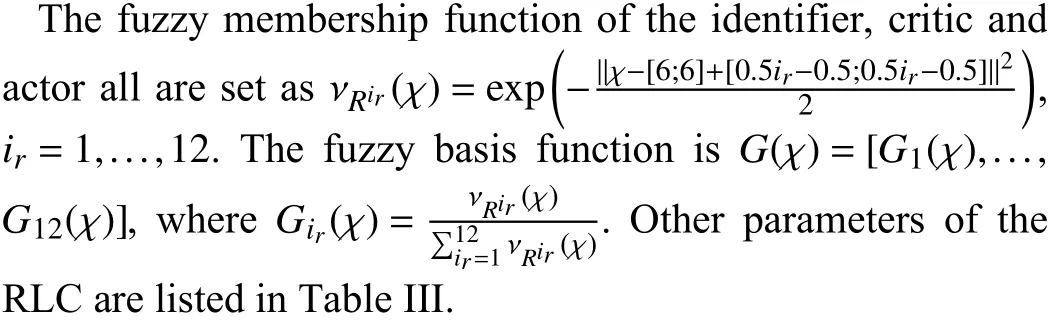
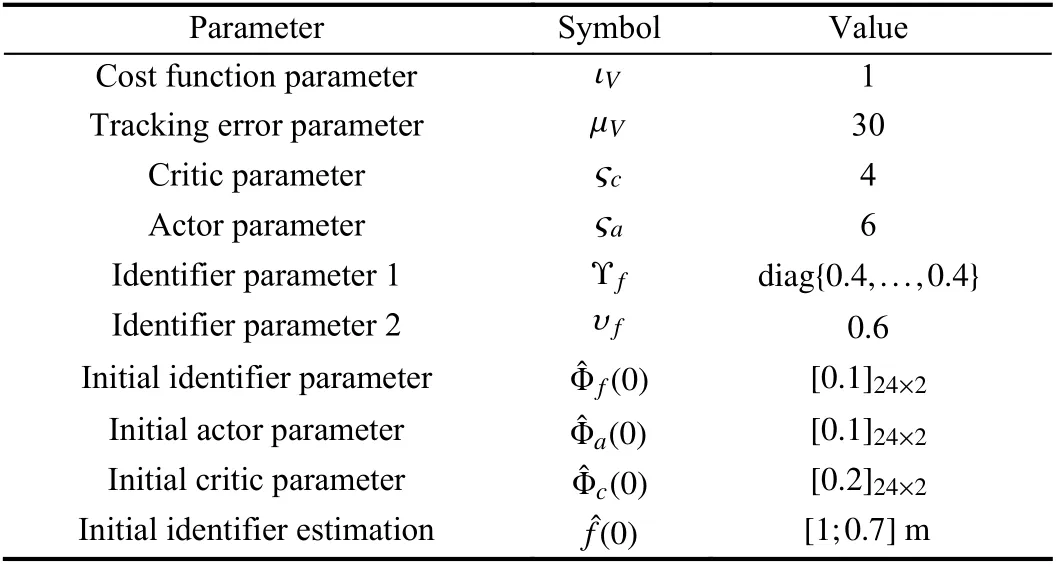
TABLE III PARAMETER VALUES OF THE RLC

B. Simulation Results

Fig. 4. The results of the agent before learning and after learning. (a) The trajectories; (b) The distances between agent and obstacles; (c) The tracking errors;(d) The mission priority adjustments.

1) The Comparison Between the Agent Before Learning and After Learning:In this comparison， the sampling frequency of RLMS is set to 100 Hz. The RLMS converges after 10 000 training episodes. Before the agent has learned， the two networks are initialized at random and the Q-value does not refer to the respectful state-behavior pair， and the agent selects composite behaviors randomly. After the agent has learned，the Q-value converges to a respectful value， and the agent selects the composite behaviors based on the learned policy.The results of the agent before learning and after learning are shown in Fig. 4， and the cost of RLMS learning is shown in Fig. 5. It can be seen from Fig. 4 that the agent has frequent and poor mission priority adjustment performance and unsuccessfully reaches the target position when the agent is not learning. Moreover， the agent achieves good mission priority adjustment performance and successfully reaches the target position when agent has finished learning. The comparison proves the effectiveness of the proposed RLMS.

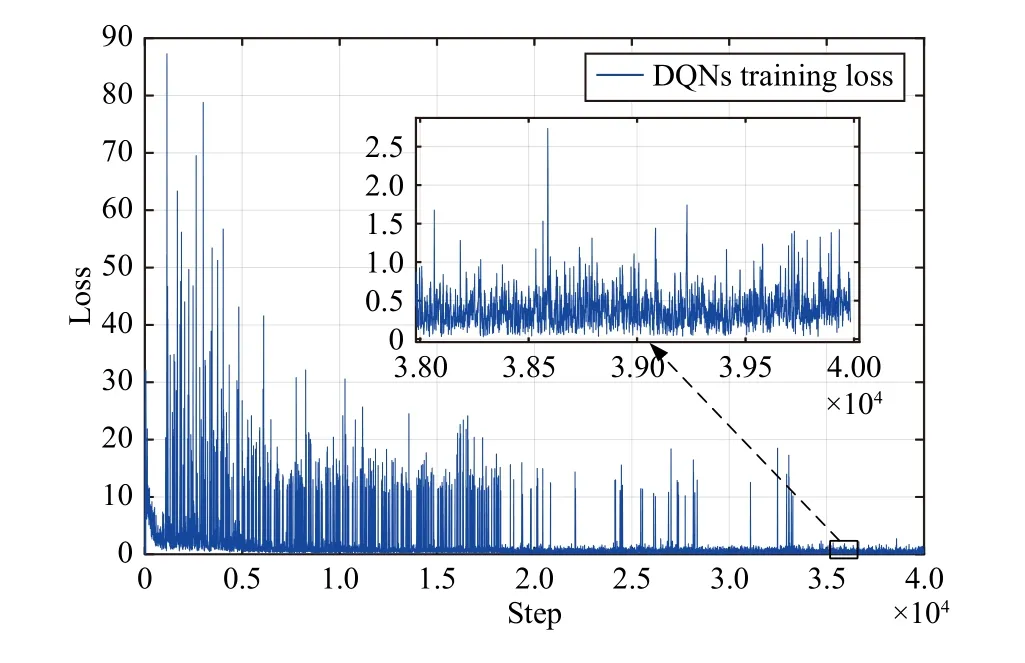
Fig. 5. The cost of the RLMS learning.

2) The Comparison Among the Proposed RLMS and Other Existing Mission Supervisors:In this comparison， the sampling frequency is first set to 100 Hz. The results of RLMS，FSAMS and MPCMS are shown in Fig. 6. It is easy to know from Fig. 6 that both RLMS and MPCMS achieve good dynamic mission priority adjustment performance， and the trajectories of agent almost coincide. However， the FSAMS has unsatisfactory mission priority adjustment performance when encountering obstacles， such as the violation of safe distance and the oscillation of trajectory. These phenomena are explained by the fact that both the RLMS and the MPCMS use the prediction state information of agent， while the FSAMS does not use it. In order to better reflect this phenomenon， we performed multiple sets of simulations at different sampling frequencies， and the results are shown in Table IV. In each sampling period， three mission supervisors need to store different data online， in which the RLMS stores the neurons of network; the FSAMS stores the variables of adjustment rule; the MPCMS stores the online calculation results of optimal priority. The online storage space requirements of three supervisors respect to the number of missions are shown in Table V. The online storage space requirements of FSAMS and RLMS are less affected by the number of missions， while the online storage space requirements of MPCMS and the number of missions is a factorial relationship. This phenomenon can be explained by fact that the MPCMS calculates and stores the optimal mission priority results at each sampling period. All results show the superiority of the proposed RLMS.

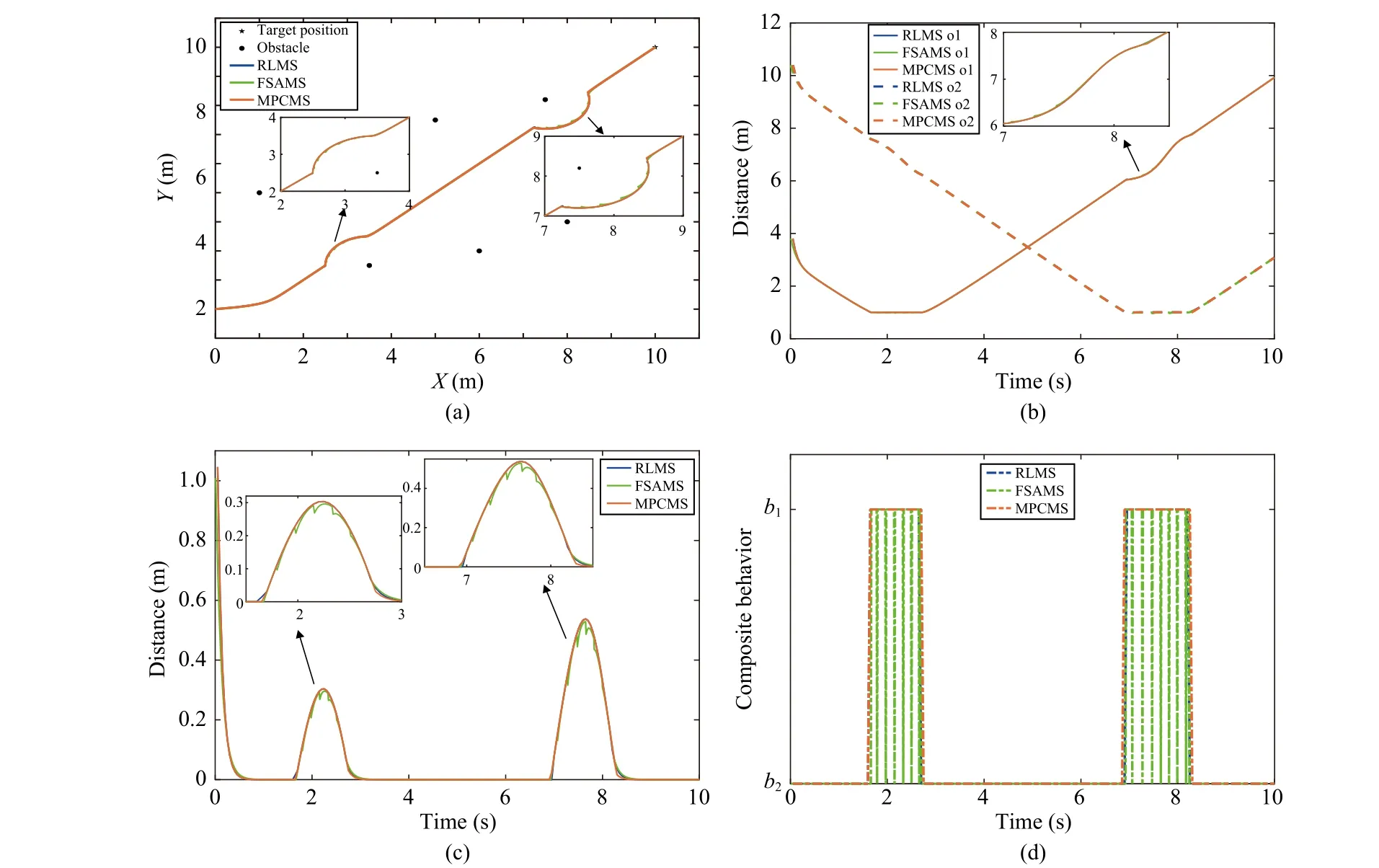
Fig. 6. The results of RLMS， FSAMS and MPCMS in the 100 Hz sampling frequency. (a) The trajectories; (b) The distances between agent and obstacles;(c) The tracking errors; (d) The mission priority adjustments.

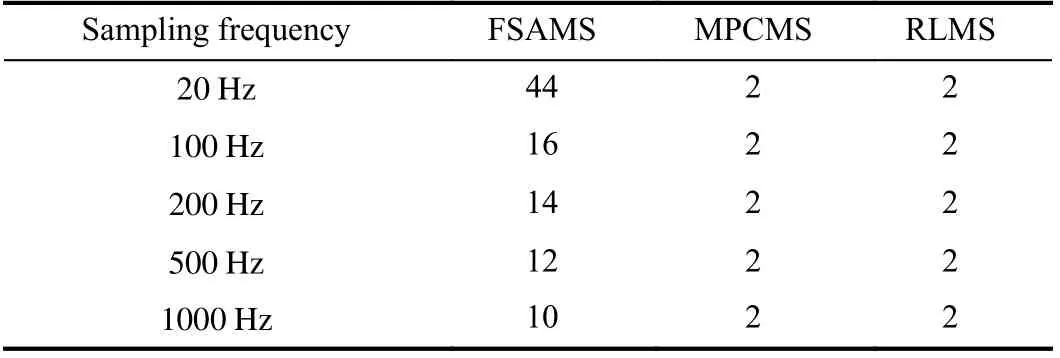
TABLE IV MISSION PRIORITY ADJUSTMENT NUMBERS OF THREE MISSION SUPERVISORS WITH DIFFERENT SAMPLING FREQUENCIES

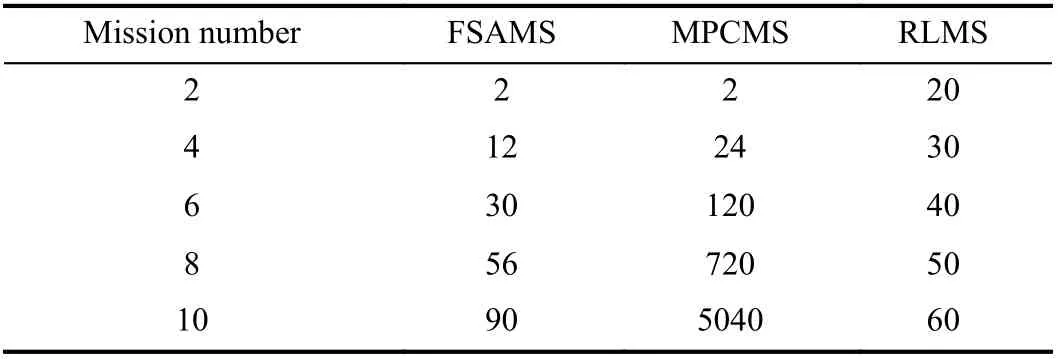
TABLE V THE ONLINE STORAGE SPACE REQUIREMENTS OF THREE SUPERVISORS WITH DIFFERENT MISSION NUMBERS

3) The Performance of the Proposed RLC:In this subsection， we verified the effectiveness of the proposed RLC.The results are shown in Figs. 7-9. Fig. 7 shows that the RLC ensures that the agent tracks the reference trajectory. Fig. 8 shows that the trajectory tracking error， the identifier parameter， the critic parameter and the actor parameter are all bounded. The cost of RLC is shown in Fig. 9. When the agent encounters the obstacle and adjusts the mission priority， the tracking error and cost of RLC increases significantly. This phenomenon is explained by the fact that the reference velocity changes significantly when the mission priority is adjusted. The tracking error of RLC is increased slightly when the mission priority is adjusted， because the RLC implements the control input in a way that balances control resources and control performance. All results prove that the proposed RLC is effective.

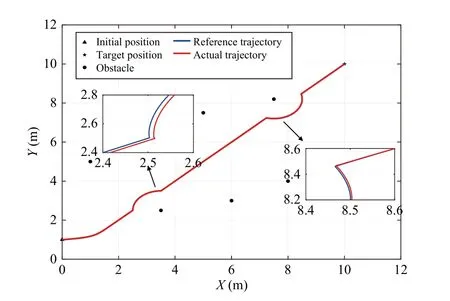
Fig. 7. The reference trajectory and the actual trajectory of the autonomous system.

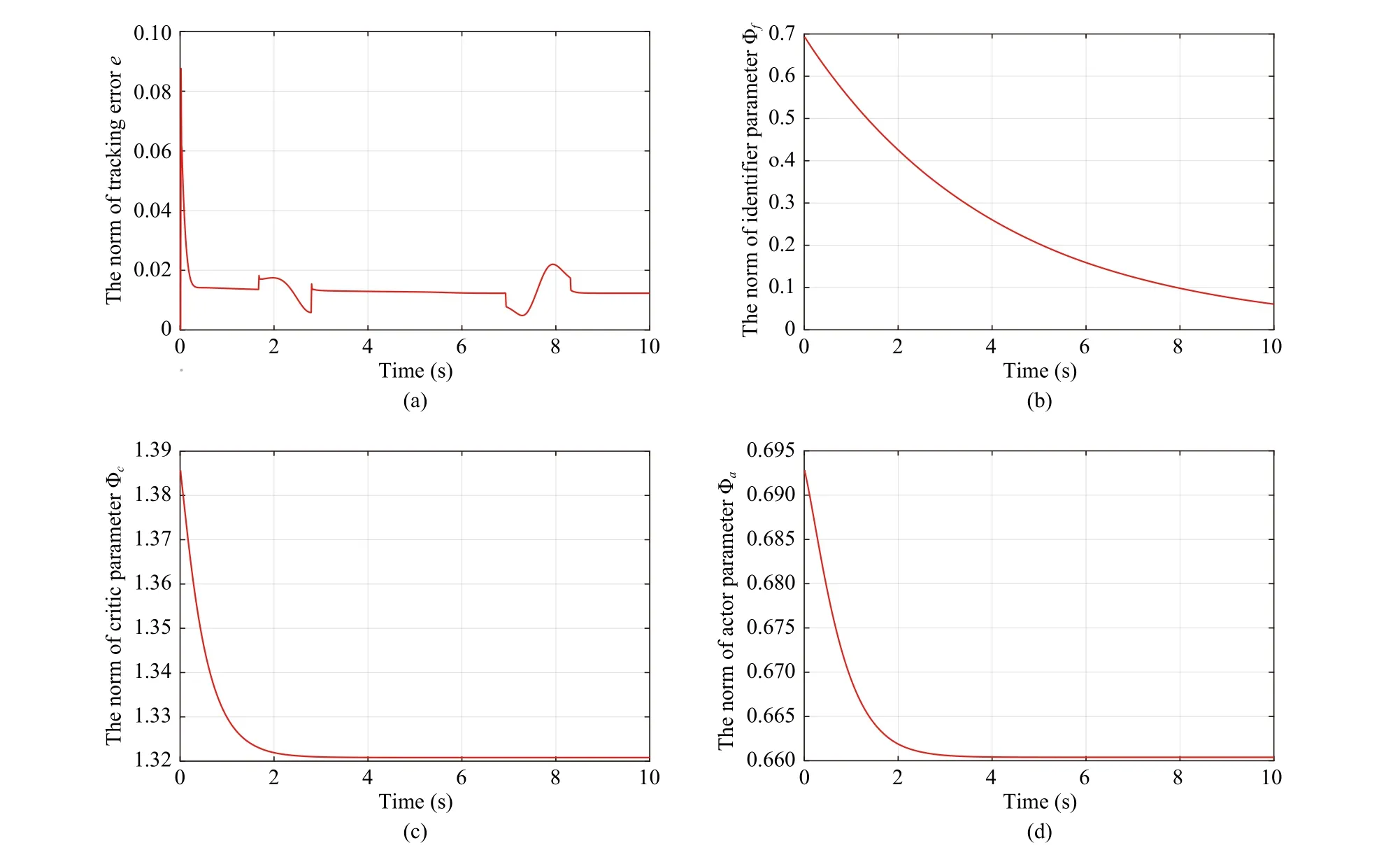
Fig. 8. The control performance results of RLC. (a) The tracking errors; (b) The identifier parameters; (c) The critic parameters; (d) The actor parameters.

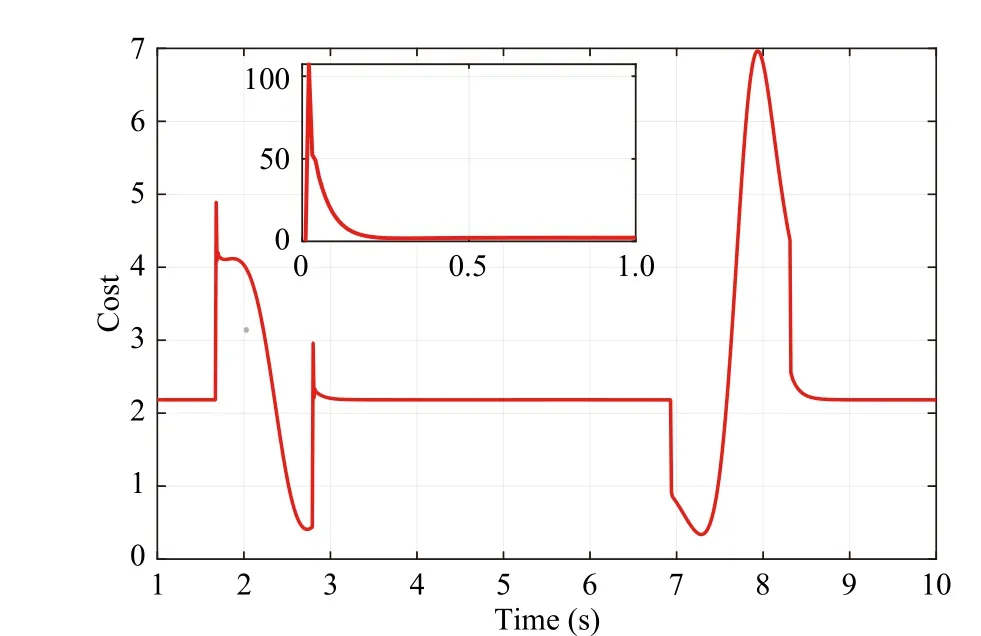
Fig. 9. The cost of the proposed RLC.

4) The Comparison Among the Proposed RLC and OtherExisting Tracking Controllers:In this subsection， the proposed RLC is compared with some existing and typical tracking controllers， such as the PID [44]， the non-robust ADP-based controller (non-RADPC) [45]， the sliding mode adaptive controller (SMAC) [21] and the finite-time adaptive fuzzy controller (FT-AFC) [46]. It is worth mentioning that the PID is a typical model-free controller; the non-RADPC is a typical non-robust optimized controller; the SMAC and the FT-AFC are typical robust non-optimized controllers. The results are show in Fig. 10. Compared with the PID， the SMAC and the FT-AFC， the RLC and the non-RADPC have smoother trajectories owing to their optimized features. The non-RADPC has the largest tracking errors due to the lack of robustness. The SMAC and the FT-AFC have relatively large control input and cost， because they provide large control inputs to ensure tracking performance. The tracking error of FT-AFC is the fastest to converge， since FT-AFC is the finitetime stable. On one hand， the RLC balances tracking error and control cost; on the other hand， the RLC has robustness using the online learning nonlinear model of agent. Therefore， the tracking error， control input and cost all are relatively small.All results show the superiority of the proposed RLC. In order to clearly reflect the efficiency of the above methods，the average time results of each iteration are shown in the Table VI. Since the iteration time of each method is at the microsecond level， they all have a real-time guarantee. On one hand， the RLC shows little difference in efficiency compared to other behavioral controllers. On the other hand， the control cost of RLC is reduced significantly， especially when mission priority is adjusted.

VI. CONCLUSION

In this paper， the shortcomings of the dynamics， optimality and intelligence of classic NSBC methodologies is overcome by utilizing RL algorithms. Since RL algorithms learn the optimal policies from interacting with a dynamic environment，the intelligent decision-making and control capabilities of an autonomous system can be improved. To reduce the dependence on human intelligence design decision rules and controllers， a novel two-layer RLBC method is proposed. By learning the optimal mission and control policies， the optimality and dynamic performance of autonomous system are guaranteed. Compared with classic NSBC methodologies，the proposed method can effectively reduce the control cost of an autonomous system to balance control performance and control resources. Specifically， in the upper layer， a novel RLMS is cleverly designed to optimally select the mission priority without artificial design rules and on-line computing.In the lower layer， a RLC is elaborately developed to optimally track the reference trajectory by using a FLS-based identifier-actor-critic architecture RL algorithm. The simulation results show the effectiveness and superiority of both the proposed RLMS and RLC. Our future work is to extend the RLMS to multi-agent systems by using multi-agent reinforcement learning algorithms and loose the Assumption 1 to deal with dynamic obstacles by resorting to multi-objective optimization methods.

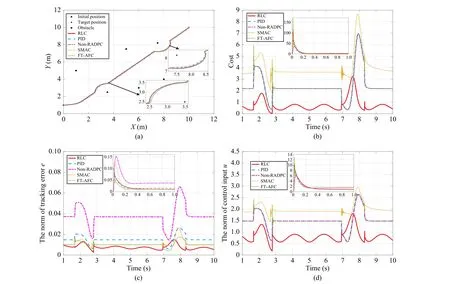
Fig. 10. The results of RLC， PID， non-RADPC， SMAC and FT-FAC in the 100 Hz sampling frequency. (a) The trajectories; (b) The costs; (c) The tracking errors; (d) The control inputs.

TABLE VI THE TIME SPENT IN EACH ITERATION OF THE FIVE METHODS

VII. SUPPLEMENTARY MATERIAL

The Python implementation of the proposed method is fully open source available at https://github.com/EzekielMok/Reinforcement-learning-mission-supervisor.git.