Data-Driven Hybrid Neural Fuzzy Network and ARX Modeling Approach to Practical Industrial Process Identification

Feng Li， Tian Zheng， Naibao He， and Qingfeng Cao

Dear editor，

This letter presents a practical industrial process identification scheme. More specifically， to improve the identification accuracy of practical process， a decoupled identification scheme is developed based on neural fuzzy network and autoregressive exogenous (ARX)model， which is based on multi-signal sources. The multiple signal sources include binary signals and random signals. Experimental results of pH neutralization process show that developed identification scheme can provide accurate identification accuracy.

Process industries may be modeled through their mechanism characteristics， called mechanism modeling. Nevertheless， it is rather difficult to select this approach because of the complexity of practical process models， which often needs to understand comprehensively practical processes characteristics. In this case， a selectable method is to establish data-driven models， which are not sensitive to process knowledge. There are many data-driven model architectures， such as Markov jump systems， state space system， and block-oriented systems. For these models mentioned， block-oriented systems can accurately various nonlinear processes [1].

Hammerstein nonlinear systems， mixing a static memoryless nonlinear subsystem and a linear dynamic subsystem， are useful configurations of block-oriented systems and has been widely applied to represent numerous practical nonlinear systems. Many methods have emerged to model the memoryless nonlinear subsystem and linear dynamic subsystem.

Modeling methods of linear dynamic subsystem mainly include impulse response， ARX， Box-Jenkins， state space model， and so on.These models can effectively describe the dynamic characteristics of the system and the interaction between variables， thus they have been widely used.

The Hammerstein nonlinear systems focus on modeling approaches of static nonlinear subsystem with high precision and extension， there are two main types of modeling approaches: linear parameter combination of known basis function and data-based nonlinear models. The former mainly include polynomials， splines，piecewise linear functions and support vector machines， but when studying multivariable systems， these methods need many parameters in modeling. Data-based nonlinear models， such as neural networks，fuzzy systems and neuro-fuzzy models， have the ability to represent complex nonlinear functions.

Thus， for practical industrial process identification， it is very important to establish the Hammerstein system which can effectively describe process characteristics. More specifically， it is to establish nonlinear subsystems with high precision and extension and linear subsystems that can meet any linear dynamic characteristics. And then effective identification methods are used to estimate of each subsystem parameters.

Related work: In recent years， a large number of substantive researches have been carried out to identify the Hammerstein system，two main identification approaches have emerged， namely synchronous identification and separation identification. The basic idea of synchronous identification approach is that parameters of hybrid nonlinear system are identified by constructing hybrid system of nonlinear subsystem and linear subsystem. Hammaret al.[2] studied output-error identification based on robust Levenberg-Marquardt algorithm for heating system benchmark. Aiming at improving convergence speed and parameters estimation accuracy， auxiliary model-based expectation maximization method is researched for Hammerstein systems with data loss [3]. Considering the Hammerstein system with dynamic disturbances and measurement noise，extended recursive least squares (RLS) identification algorithm is derived [4]. Based on data filtering technique， the parameter identification problem of multiple-input single-output Hammerstein system are considered [5]. Combining hierarchical identification principle and model decomposition technique， parameter estimation problems of two-input single-output Hammerstein finite impulse response systems are discussed [6].

Although these identification approaches mentioned can complete parameters identification， they contain parameters product term and need to be further separated using parameters separation methods，such as singular value decomposition and average method. Therefore， identification accuracy is reduced and computational complexity is increased. In addition， their nonlinear subsystems are modeled by polynomial models. If nonlinearities are not polynomial models， these approaches do not converge [7].

On the contrary， the principle of separation identification approach is to separate the identification problems of static nonlinear subsystem and linear dynamic subsystem by estimating immeasurable intermediate variables， thus nonlinear subsystem parameters and linear subsystem parameters are carried out independently. Based on special input excitation， Kothariet al.[1] adopted a new parameter identification strategy for a block-oriented Hammerstein process using Haar wavelet operational matrix. To solve the enhanced oil recovery problem for alkali-surfactant-polymer (ASP) flooding， Liet al.[8] used iterative dynamic programming optimization to study biorthogonal spatial-temporal Hammerstein modeling. To compensate for noise in the output， correlation analysis-based error compensation recursive least-square method is suggested by Li and Jia[9] for the Hammerstein model. Vanbeylenet al.[10] developed blind identification method for discrete-time Hammerstein systems from output measurements. A parametric identification for parallel Hammerstein systems using a three-step procedure is presented [11].

Compared with the existing synchronous algorithms for Hammerstein systems， a major advantage of these methods is that nonlinear subsystem parameters and linear subsystem parameters are identified independently， which improve identification accuracy. However，they only consider the interference of white noise， without taking into account colored noise.

Recently， some novel optimization algorithms， such as populationbased optimization method [12]， dwarf mongoose optimization algorithm [13]， Ebola optimization search algorithm [14]， and reptile search algorithm [15]， have been presented to handle successfully system design or engineering design， which would inspire researchers to take interest. Also， these optimization methods can be used for Hammerstein system identification.

Problem statements: Neural network and fuzzy system have been applied widely to nonlinear system modeling since that they show strong nonlinear approximation ability in recent years. It should be noted that neural networks have strong ability of the self-learning，but it is lack of reasoning ability of human brain. On the contrary， the fuzzy systems itself have no self-learning ability， which exists some limitations for practical application. Therefore， a significant technique is to apply fuzzy neural network that combines fuzzy reasoning ability of fuzzy system and self-learning of neural network as the static nonlinear subsystem. For the linear dynamic subsystem， ARX model as our discussion， owing to the potentiality that the ARX model can approximate any linear dynamical system as well as its simplicity.

Considered thatv(k) in Fig. 1 is an experimentally immeasurable quantity in the Hammerstein system， butv(k) may describe system dynamic characteristics， which increases identification difficulty.Since the static nonlinear subsystem is not activated under binary signals， specifically， the intermediate variablev(k) also shows binary signals with same frequency and different amplitude asu(k) [16].Thus， using the input approximation instead of the intermediate variable， parameters identification of nonlinear subsystem and linear subsystem can be identified separately.

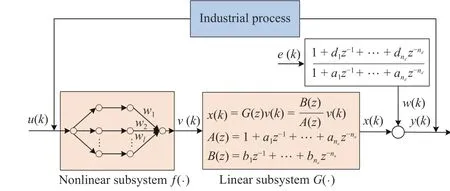
Fig. 1. Identification model of industrial process using Hammerstein system.

The main contributions are as follows:

1) Unlike to most synchronous identification， the presented method is used for separating parameters identification of nonlinear subsystem and linear subsystem， which simplifies identification process and improves identification precision.

2) By using the recursive extended technique， the influence of output noise to parameter identification accuracy is reduced.

3) For the unmeasurable intermediate variables in the identified Hammerstein system， the auxiliary model technique ensures that consistent estimation of system parameters can be obtained.

Proposed identification scheme: A three-stage separation identification scheme is designed based on multiple signals that consist of binary signals and random signals， which is called multiple signal sources Hammerstein system identification (MSS-HI)， as shown in Fig. 2. The purpose of scheme studied is to identify unknown parameters of neural fuzzy network， ARX model， and noise model.In Stage 1， the characteristics of nonlinear subsystem are not activated using binary signals， and then parameters of ARX model and noise model are identified by recursive extended least squares algorithm. In Stage 2， the width and center of neural fuzzy network are adjusted by cluster algorithm. In Stage 3， the weights of neural fuzzy network are estimated using auxiliary model-based recursive extended least squares algorithm.

The specific processes of three-stage identification are depicted as below:

Stage 1: The binary signalsu1(k) are input to the listed system and corresponding outputs arey1(k). The unmeasurable noise termse(k)of the identified system are replaced by its estimation term， so recursive extended least square approach is applied for identifying parameters of ARX model and noise model. The identification procedures of this stage are given by

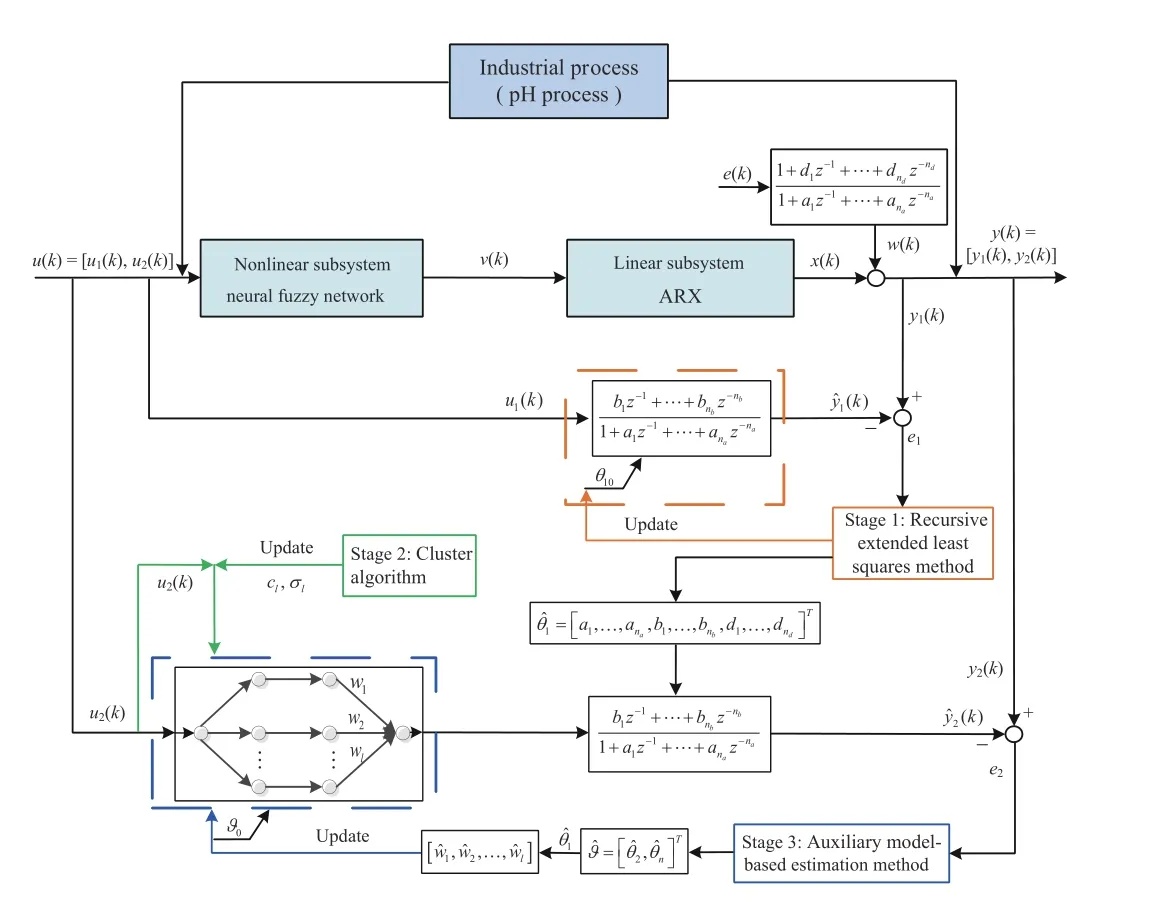
Fig. 2. Identification scheme of Hammerstein nonlinear system.

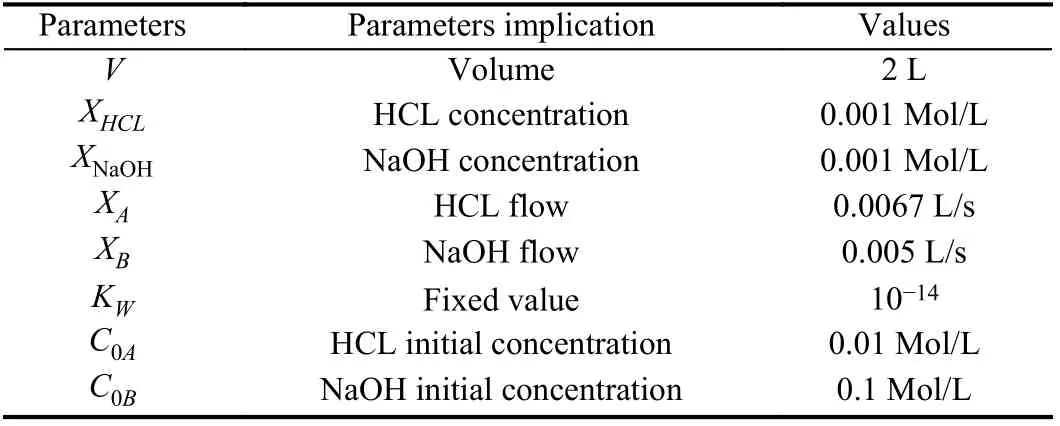
Table 1.Nominal Values

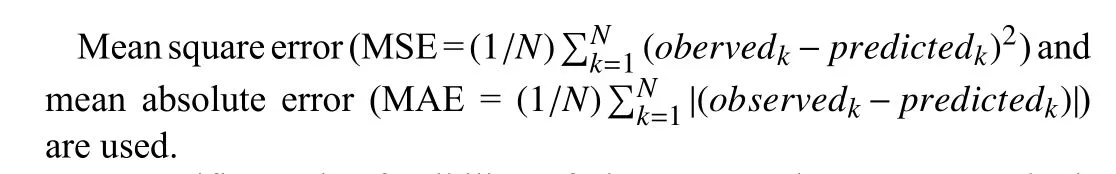
To certificate the feasibility of the presented MSS-HI method，polynomial-based Hammerstein model (PHM) method [20] and filtering-based recursive least squares algorithm (FRLS) [21]， and previous work [9] are compared. Fig. 3 shows parameters estimation error of four identification algorithms for pH process. From Fig. 3，the presented method achieves a faster convergence rate than other three algorithms， which mainly lies in that the proposed method applies separation identification technique to avoid the separation of parameter product terms appeared in [20] and [21]， and estimates noise model parameter instead of noise variance in [9].

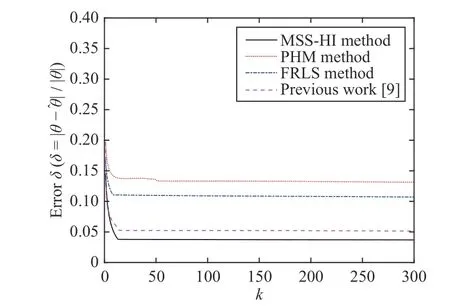
Fig. 3. Estimation error of four identification algorithms for pH process.

Remark 1: For industrial process identification， it is significant important to establish a process model that can meet the characteristics of actual process and identify it by using feasible method.The proposed separation identification scheme for the pH process modeled by Hammerstein system solves two challenge problems.Firstly， from the perspective of identification accuracy， the neural fuzzy network avoids the inevitable restrictions on nonlinear subsystem encountered by using polynomial method. Furthermore， in terms of modeling， the proposed method applies separation identification technique to avoid the separation of parameter product terms appeared in [20] and [21]， improving identification accuracy.

Random signals with [-0.5，0.5] are used for prediction purposes，the prediction outputs of pH process using three approaches are compared in Fig. 4 and Table 2. It is obvious that MSS-HI outperforms PHM and FRLS in terms of prediction accuracy. The simulation results present that the prediction precision of MSS-HI is higher than that other two algorithms in MSE and MAE. In experiments， the signal noise ratio (SNR) is set as 7.13%，λ= 0.01，ρ=2. The output noise affects prediction performance of system， with the increase of SNR， prediction performance decreases slightly.

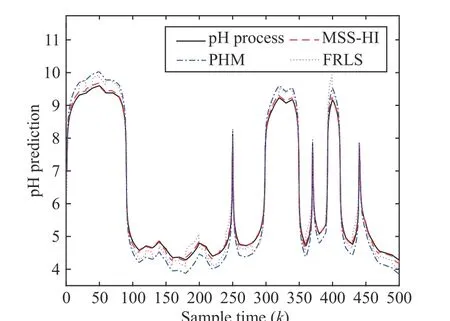
Fig. 4. Comparisons of prediction output of pH process.

Table 2.Comparison of MSEs and MAEs

Remark 2: Simulation results show that the nonlinear subsystem can be approximated exactly using suitable parametersλandρ.Smallerλand largerρlead to smaller model error， but slower convergence. Thus， the parameters selection should balance system error and convergence speed.

Remark 3: The strengths of the developed method mainly have two aspects: Firstly， the characteristics of nonlinear subsystem are not activated using binary signals， thus nonlinear subsystem parameters and linear subsystem parameters are identified separately， reducing identification complexity. Secondly， the auxiliary model technique and recursive extended principle ensure that parameters consistent estimation is obtained. In terms of weaknesses， the parameters selection ofλandρshould effectively balance system error and convergence speed. In addition， the correlation of noise at different times needs to be further studied.

Conclusions: This letter presents a separation identification scheme for pH process， in which the pH process is modeled by Hammerstein system with neural fuzzy network and ARX model. In terms of research contributions， the designed multi-signals are used to realize identification separation of the Hammerstein system， which improves identification precision. In view of the unmeasurable intermediate variables in identified Hammerstein system， the auxiliary model technique is used to obtain parameters consistent estimation. From the perspective of research limitations， the colored noise considered is only linear combination driven by white noise，the correlation of noise at different times is not researched. Our future works will be carried out from two aspects: firstly， some novel optimization algorithms [12]-[15] can be used for identification of practical process represented by Hammerstein system. In addition，the nonlinear subsystem of the Hammerstein system is modeled by deep neural network models [22].

Acknowledgments: This work was supported by the National Natural Science Foundation of China (62003151)， the Natural Science Foundation of Jiangsu Province (BK20191035)， and the Changzhou Sci&Tech Program (CJ20220065).