Symmetry and Nonnegativity-Constrained Matrix Factorization for Community Detection

Zhigang Liu， Guangxiao Yuan， and Xin Lu o

Dear editor，

This letter presents a novel symmetry and nonnegativity-constrained matrix factorization (SNCMF)-based community detection model on undirected networks such as a social network. Community is a fundamental characteristic of a network， making community detection a vital yet thorny issue in network representation. Owing to its high interpretability and scalability， a symmetric nonnegative matrix factorization (SNMF) model is frequently adopted to address this issue. However， it adopts a unique latent factor (LF) matrix for representing an undirected network’s symmetry， which leads to a reduced latent space that impairs its representation learning ability.Motivated by this discovery， the proposed SNCMF model innovatively adopts the following three-fold ideas: 1) Leveraging multiple LF matrices to represent a network， thereby enhancing its representation learning ability; 2) Introducing a symmetry regularization term that implies the equality constraint between multiple LF matrices to illustrate the network’s symmetry; and 3) Incorporating graph regularization into the model to preserve the network’s intrinsic geometry. Experimental results on several real-world networks indicate that the proposed SNCMF-based community detector outperforms the benchmark and state-of-the-art models in achieving highly-accurate community detection results.

Networks are ubiquitous in the age of the Internet. In general，multitudinous entities in a real system and their interactions form an undirected network， e.g.， wireless sensor networks and social networks. Commonly， a community in a network can be considered as its sub-graph in which a group of network nodes are connected tightly with each other through direct or indirect connections.Communities are pervasive in a network， and play a significant role in revealing its mechanism of organization and operation. Based on accurately detected communities， various network analysis tasks are facilitated， such as graph classification and social recommendation.

Related work: To date， community detection has attracted great attention from researchers， leading to a pyramid of detection models[1]. Among them， a nonnegative matrix factorization (NMF) model[2] has proven to be highly scalable and interpretable. Hence， it has been frequently applied to community detection. Given a network， an NMF-based detector works by building a low-rank approximation to the target adjacency matrix relaying on a set of nonnegative LF matrices. The achieved LFs can be considered as either the softthreshold to identify the community of a specific entity， or the input of a hierarchical community detector. For example， Lenget al. [3]present a graph-regularizedLpsmooth NMF model for data representation， which considers the intrinsic geometric information of target data and generates a smooth and stable solution. By incorporating the prior information into the factorization process， Maet al. [4] present a semi-supervised joint NMF model to improve the community detection performance in a multi-layer network.

The above-mentioned approaches， despite of their efficiency in community detection， fail to correctly represent a given undirected network’s intrinsic symmetry. SNMF works by adopting a unique LF matrix to learn a low-rank approximation to a symmetric matrix，thereby correctly representing its symmetry， which is equivalent to the Laplacian-based spectral clustering and kernelk-means， and can well be utilized to perform community detection. Yanget al. [5]present a unified interpretation to SNMF-based community detectors.Yeet al. [6] propose a homophily preserving SNMF model that combines the link topology and node homophily of a network，thereby better describing community structures. Luoet al. [7]propose to linearly or non-linearly control the scaling-factor of a nonnegative multiplicative update scheme for a graph regularized SNMF model， resulting highly-accurate community detectors.

However， existing SNMF-based models commonly adopt a single LF matrix only for ensuring its rigorous symmetry， which is actually a so strong constraint that restricts its representation learning ability[8]. Thus， this work aims to design an SNCMF-based community detector that represents an undirected network’s symmetry with multiple LF matrices， thereby achieving accurate results.

Fig. 1. Workflow for an NMF-based community detector.

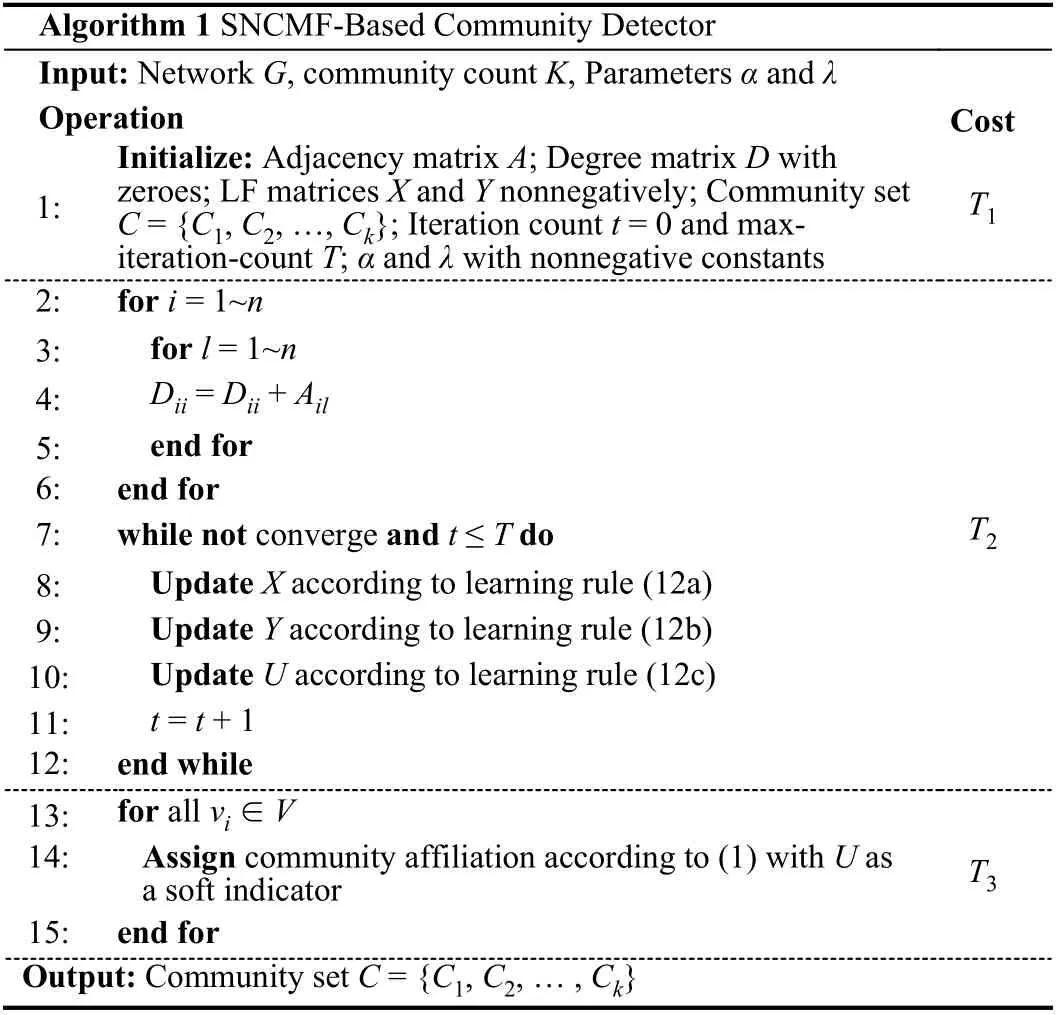
Algorithm 1 SNCMF-Based Community Detector Input: Network G， community count K， Parameters α and λ Operation Cost 1:Initialize: Adjacency matrix A; Degree matrix D with zeroes; LF matrices X and Y nonnegatively; Community set C = {C1， C2， …， Ck}; Iteration count t = 0 and maxiteration-count T; α and λ with nonnegative constants T1 2: for i = 1～n T2 3: for l = 1～n 4: Dii = Dii + Ail 5: end for 6: end for 7: while not converge and t ≤ T do 8: Update X according to learning rule (12a)9: Update Y according to learning rule (12b)10: Update U according to learning rule (12c)11: t = t + 1 12: end while 13: for all vi ∈ V 14: Assign community affiliation according to (1) with U as a soft indicator T3 15: end for Output: Community set C = {C1， C2， … ， Ck}

An SNMF-based model introduces strong symmetry into the model for precisely representing the symmetry of an undirected network.However， the unique LF matrix also leads to shrinkage of its LF space， which reduces its representation learning ability toA， as well as its performance for community detection.

Proposed community detector: A unified SNCMF model for highly-accurate community detection is presented. Its main idea is to introduce equality-constraint-based symmetry regularization along with the graph regularization into its objective， thereby achieving highly-accurate representation to the target network.

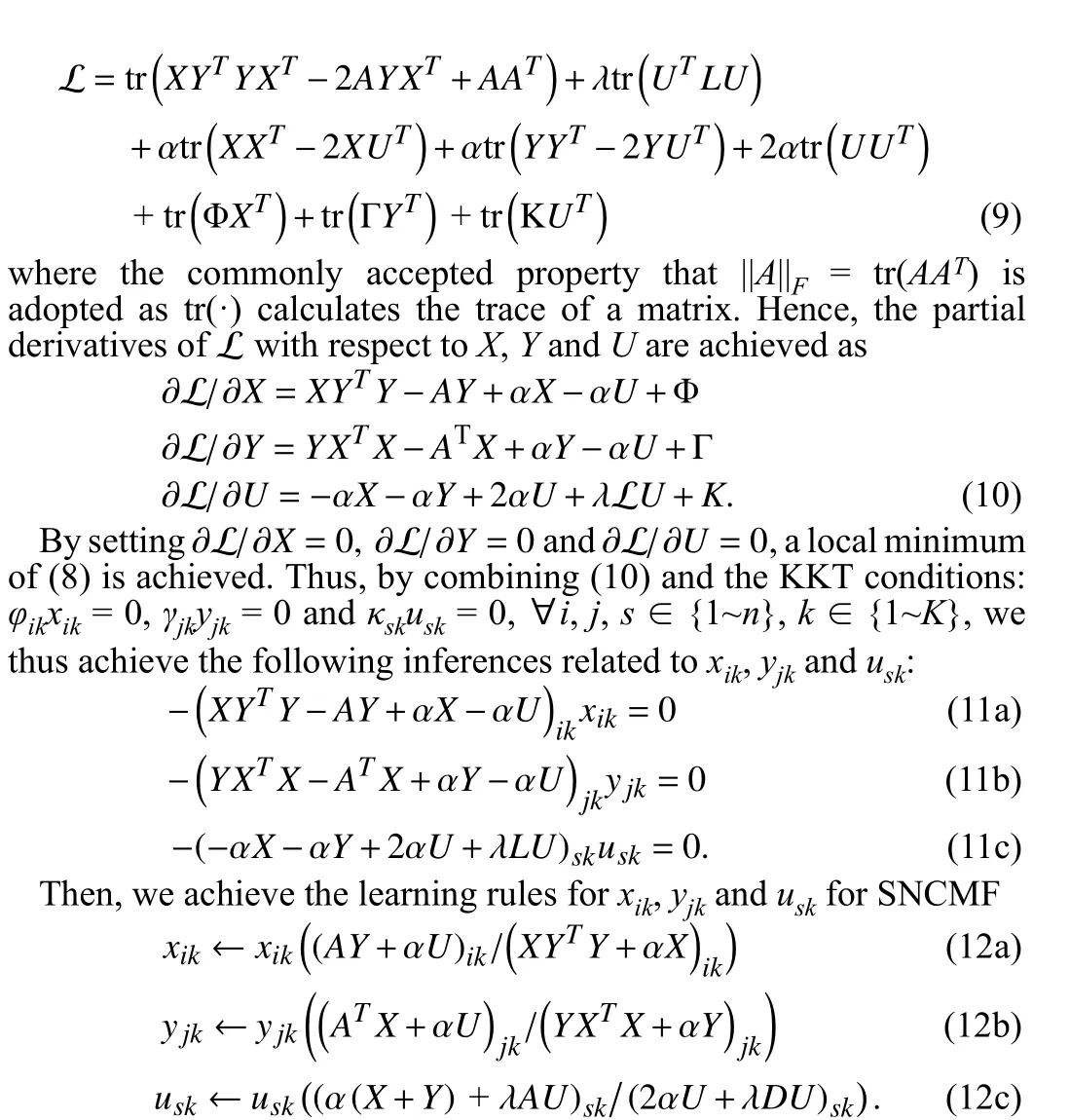
Hereto， an SNCMF-based community detector is obtained. Note that we takeUas the indicator matrix for final community division，since it actually shares the information from bothXandY.

With (12)， we thus design an algorithm for the proposed SNCMFbased community detector in Algorithm 1. According to the details shown in Algorithm 1， the time cost of SNCMF can be summarized as:TSNCMF=T1+T2+T3= Θ(n2)+Θ(n2TK)+Θ(nK) ≈ Θ(n2TK)， where the lower-order-terms are dropped sinceK＜＜n. In practice， sinceKandTare small and positive constants， the computational cost of SNCMF is approximately quadratic with the node count， which is equal to most existing NMF-based community detectors [2]-[9].Note that the time cost of the model can be greatly reduced via the help of GPU.

Experiments: For evaluating the performance of SNCMF， six publicly-available networks from real applications are used in our experiments as shown in Table 1. Normalized Mutual Information(NMI) for measuring the similarity between the resulted community assignment and the ground-truth community information is taken as the indicator to evaluate the detection accuracy of involved models[5]， [7]， [8]. Note that the NMI is in the scale of (0， 1)， as large NMI stands for high performance of a detection model.

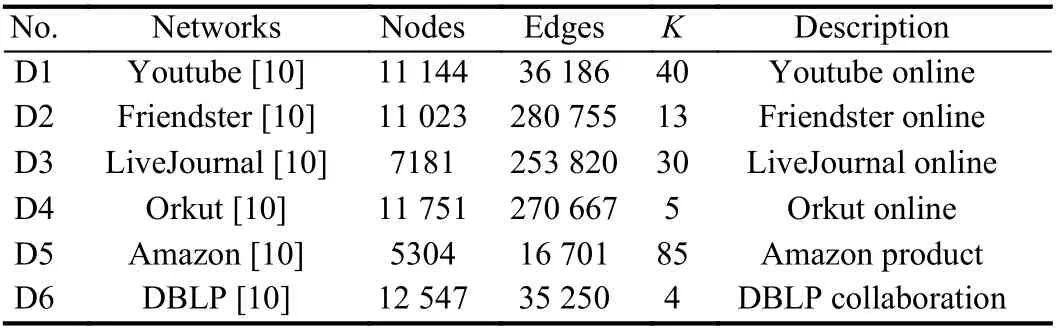
Table 1.Details of Adopted Networks

We compare our method with nine benchmark and state-of-the-art models: NMF [2]， GNMF [11]， SNMF [5]， GSNMF [5]， NSED [12]，SymNMF [13]， DeepWalk [14]， LINE [15]， and HPNMF [6].

To obtain objective experimental results， hyper-parameters are set as follows. For LINE and DeepWalk， we perform the experiments by the default settings in their official toolkits. For graph regularized models， i.e.， GNMF， GSNMF and SNCMF， the graph regularization coefficientλis uniformly set at 100 according to [11]. For HPNMF，both of its parameters， i.e.，λandγ， are set at one， according to [6]. In addition， for SNCMF， we set its symmetry regularization parameter，i.e.，αat 2–8uniformly on all datasets.

In addition， the final experiment results are achieved by repeating each separate experiment 20 times with various initial hypotheses.Average NMI values of ten involved methods on six social networks are summarized in Table 2. Moreover， the corresponding statistical test results， i.e.， Win/Loss counts， Friedman ranks， andp-value ofWilcoxon test， are also provided in Table 2. From the results， we have the following findings:

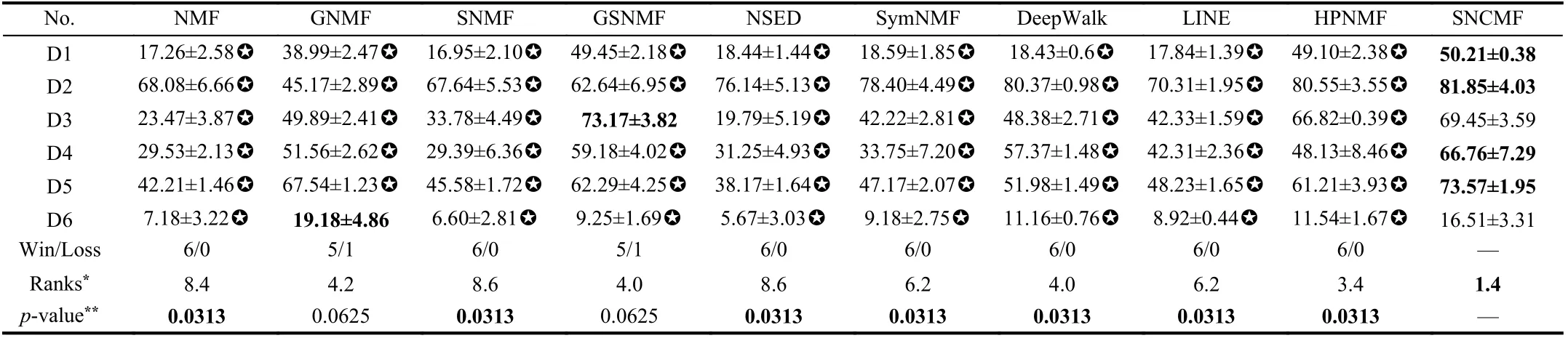
Table 2.Community Detection Performance (NMI%±STD%) of Tested Models on Each Network (✪ Indicates That SNCMF Win the Compared Models)

1) Symmetry regularization enables an NMF-based community detector to achieve higher accuracy. As shown in Table 2， we see that SNCMF outperforms GNMF on five testing cases out of six in total significantly with a confidence level at 90%.

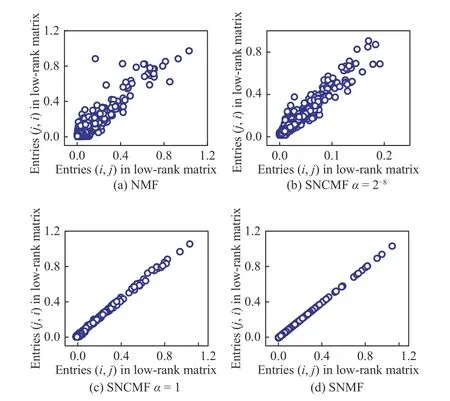
Fig. 2. Data distribution in Aˆ on D1.

Conclusions: This work presents a novel SNCMF model that adopts both symmetry and graph regularizations to accurately represent an undirected network. Empirical studies on six real-world social networks demonstrate that an SNCMF-based community detector achieves higher community detection accuracy than the benchmark and state-of-the-art methods. Thus， we conclude that the representation to the symmetry of a target undirected network and the LF space should be well balanced as in an SNCMF model for achieving highly accurate community detection results.

We plan to handle the problem of hyper-parameter adaptation via evolutionary computation techniques such as the particle swarm optimization (PSO) algorithm [16] in our future work.

Acknowledgments: This work was supported in part by the CAAI-Huawei MindSpore Open Fund (CAAIXSJLJJ-2021-035A)，and the Doctoral Student Talent Training Program of Chongqing University of Posts and Telecommunications (BYJS202009).