Adaptive Containment Control for Fractional-Order Nonlinear Multi-Agent Systems With Time-Varying Parameters

Yang Liu， Huaguang Zhang，，， Yingchun Wang，，， and Hongjing Liang，，

Abstract—This paper investigates adaptive containment control for a class of fractional-order multi-agent systems (FOMASs)with time-varying parameters and disturbances. By using the bounded estimation method， the difficulty generated by the timevarying parameters and disturbances is overcome. The command filter is introduced to solve the complexity problem inherent in adaptive backstepping control. Meanwhile， in order to eliminate the effect of filter errors， a novel distributed error compensating scheme is constructed， in which only the local information from the neighbor agents is utilized. Then， a distributed adaptive containment control scheme for FOMASs is developed based on backstepping to guarantee that the outputs of all the followers are steered to the convex hull spanned by the leaders. Based on the extension of Barbalat’s lemma to fractional-order integrals， it can be proven that the containment errors and the compensating signals have asymptotic convergence. Finally， three simulation examples are given to show the feasibility and effectiveness of the proposed control method.

I. INTRODUCTION

DURING the past few decades， there has been a great deal of research in regards of the cooperative control of the nonlinear multi-agent systems (MASs)， such as [1]–[6]. Early works focused on MASs with integer-order dynamics.However， some phenomena can be explained by the cooperative group behavior of agents with fractional-order dynamics rather than classical integer-order dynamics， such as robot formation [7] and high-speed aircraft formation. Then，the cooperative control for nonlinear fractional-order multiagent systems (FOMASs) has been developed. In [8]， an adaptive feedback control was constructed to guarantee consensus control for FOMASs under direct topology.Further， the authors designed fault-tolerant consensus control for the FOMASs in [9]. Note that the existing results for the fractional-order nonlinear systems were limited to timeinvariant systems (the uncertain parameters were constants).However， the time-varying parameters and disturbances exist in the practical operating environment， which affect the control performance of the systems.

The adaptive backstepping method， as a classical control method， has been widely used for the control design of the nonlinear systems in the lower triangle structure [10]–[13].Especially with the development of the intelligent algorithms，such as fuzzy systems [14]–[17] and neural networks[18]–[23]， the adaptive control methods for uncertain nonlinear systems have been greatly promoted. For nonlinear systems with uncertain time-varying parameters， the adaptive control method is still valid， and some pioneering works have been proposed. In [24]， the authors proposed the so-called congelation of variables method， and a structured adaptive approach was provided for the strict-feedback nonlinear system. For time-varying MASs， a cooperative tracking control was designed in [25]， in which tracking errors were steered to converge into the neighborhood of origin. In [26]， a smooth nonlinear function was utilized to compensate for time-varying parameters and disturbances， and asymptotic tracking was achieved. In [27]， two identification algorithms were developed to identify the time-varying parameters in finite-time and fixed-time. In [28]， three stable adaptive tracking schemes for multi-input-multi-output nonlinear systems with time-varying control coefficients were designed.However， all the results are concerned with integer-order nonlinear systems. To the best of our knowledge， there is no result for the fraction-order nonlinear system with timevarying parameters. Due to the specific characteristics of the fractional-order calculation， the obtained results on the integer-order dynamic system can not be directly extended to the fractional-order case. As a result， it is important to develop the control method for the fractional-order nonlinear system with time-varying parameters.

It is noteworthy that the problem of “complexity explosion”with adaptive backstepping control cannot be ignored. To address this concern， scholars have been seeking a solution. In[29]， fractional dynamic surface technology was constructed，in which a novel signal was generated to substitute the virtual control signal in the controller design. In [30]， a fractionalorder command filter-based adaptive backstepping control was developed for the fractional-order nonlinear system， in which the computational burden was effectively reduced.Nevertheless， most existing references only focused on the single fractional-order system. Little effort is devoted to exploring command filter-based adaptive control for the FOMASs.

Motivated by the above-mentioned content， this paper investigates containment control for nonlinear FOMASs with time-varying parameters and disturbances. As one of the basic cooperative behaviors， containment control involves steering each follower to the convex hull spanned by multiple leaders[31]–[34]. Such a problem is not trivial and rather challenging due to the following reasons: On the one hand， due to unknown time-varying parameters and disturbances， it is necessary to identify uncertainties and try to compensate for them in the controller design. On the other hand， due to the distributed containment error containing information from neighborhood agents， then， determining how to effectively construct the compensating signals and coordination transformations is complex， which is a significant difference from the command-filter control for the single system. The contributions of this paper are threefold:

1) This paper is the first effort to explore adaptive containment control for the nonlinear FOMASs with unknown time-varying parameters and disturbances. The bounded estimation approach is designed to overcome the difficulty generated by time-varying parameters and disturbances.

2) The command filter is introduced to reduce the complexity of controller design in the backstepping method.What’s more， a novel distributed error compensating scheme is constructed to counteract the effect of the filter errors，which only utilizes local information from the neighborhood agents.

3) The hyperbolic tangent function with time-varying integrable function is skilly incorporated into the controllers and the compensating signals， which can effectively compensate for the time-varying parameters， disturbances and filter errors.

The remainder of this paper is arranged as follows. The preliminary fractional-order calculation and graph theory are given， and the control problem is stated in Section II.A recursive procedure based on the command filter backstepping method is developed， and the stability is analyzed in Section III. Simulation results and conclusions are shown in Sections IV and V， respectively.

II. PRELIMINARY

A. Fractional Calculation

At first， some definitions and lemmas of the fractional calculation are provided as follows.

B. Graph Theory

C. Problem Statement

Remark 1:Assumptions 1 and 2 are the general conditions in the command filtered backstepping， such as [29]， [30].Assumption 3 is a common condition for the containment control of the MASs， which can confirm that no agent is isolated. Assumption 4 is a necessary condition for the systems to be controllable.

The control objective of this paper is to design a distributed cooperative control scheme such that all the output signals of the followers are driven to converge into the convex hull spanned by the leaders.

III. THE CONTROL DESIGN AND STABILITY ANALYSIS

In this section， combining the command filtered backstepping and the bounded estimation approach， an adaptive distributed control scheme for the FOMASs will be established， in which a class of novel coordination transformations and a distributed compensating scheme are constructed.

A. The Control Design for The FOMASs

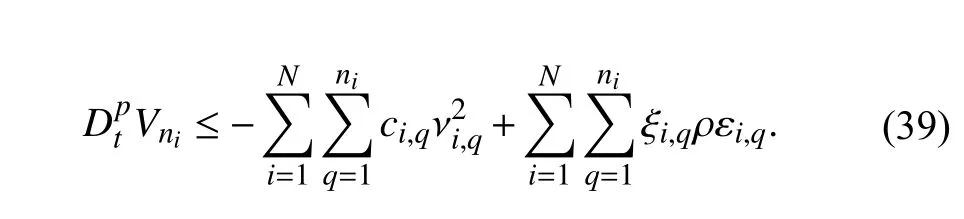
B. The Stability Analysis

Theorem 1:Consider the FOMASs consisting ofNfollowers (1) andMleaders. Suppose that Assumptions 1–4 hold and the initial conditions are satisfied. Then， under the control input (17)， (31)， (37) and the adaptive laws (18)， (32)，(38)， the containment control can be achieved， and all the signals in the control system are bounded. The compensating signals (5)-(8) have an asymptotic convergence.

Proof:Performing the fractional integration on both sides of inequality (39) gives

Fig. 1. The topology of the leaders and followers for Example 1.

IV. SIMULATION

Three examples will be given to verify the feasibility and validity of our proposed method in Section III. The simulations are implemented in MATLAB R2018b and SIMULINK， and the configuration of the computer is Intel (R)core (TM) i5-8400 CPU @ 2.80 GHz. In simulation， a MATLAB FOTF toolbox for dealing with fractional calculus and fractional control is employed， which can be obtained from the references [42]， [43].

Example 1:A group of networked FOMASs consisting of two leaders and three followers is considered. The communication graph between the followers and leaders is shown in Fig. 1. Then， the Laplace matrix is given as

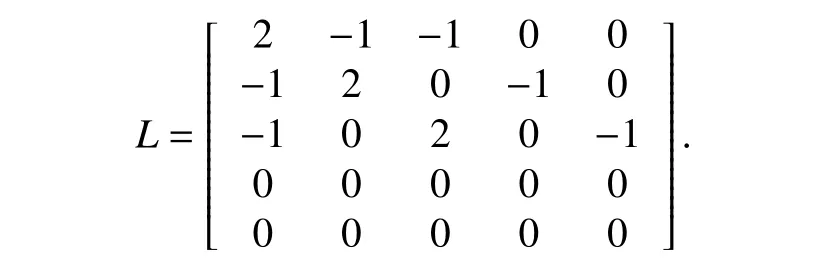
The dynamic of each follower agent is described as follows:

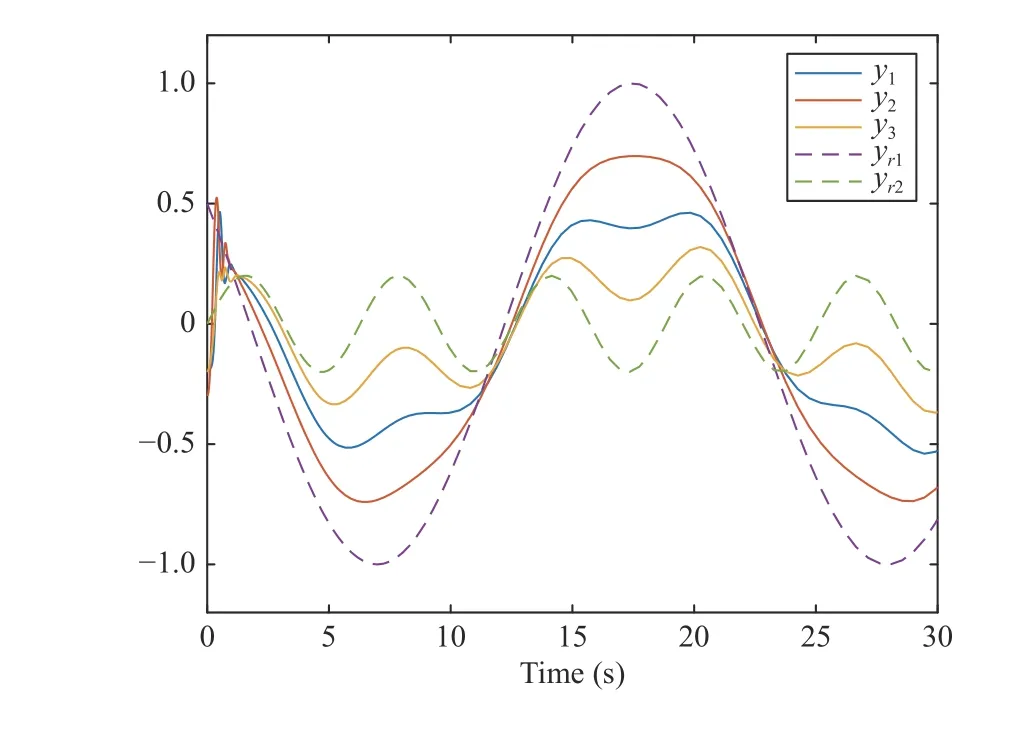
Fig. 2. The performance of the containment control strategy.

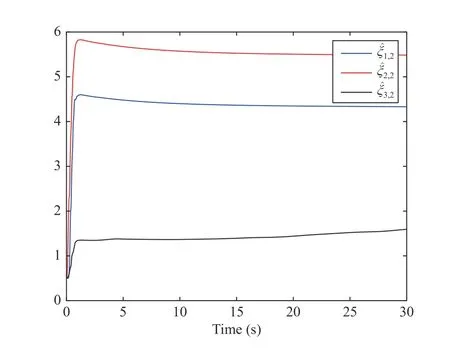
Fig. 3. The trajectories of the adaptive parameters ξ ˆi，2.

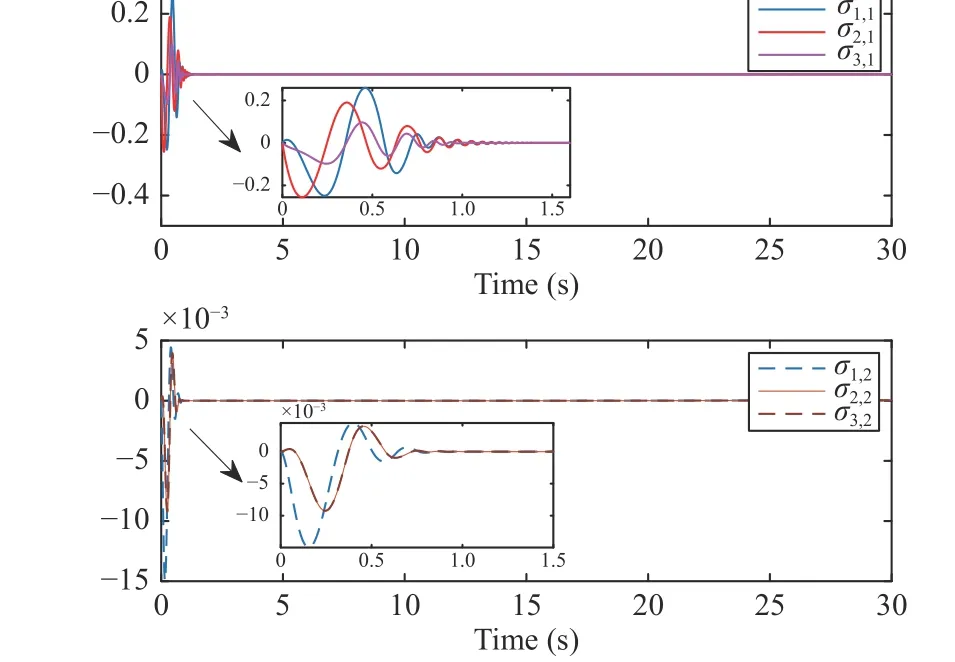
Fig. 4. The trajectories of compensating signals σ i，j.

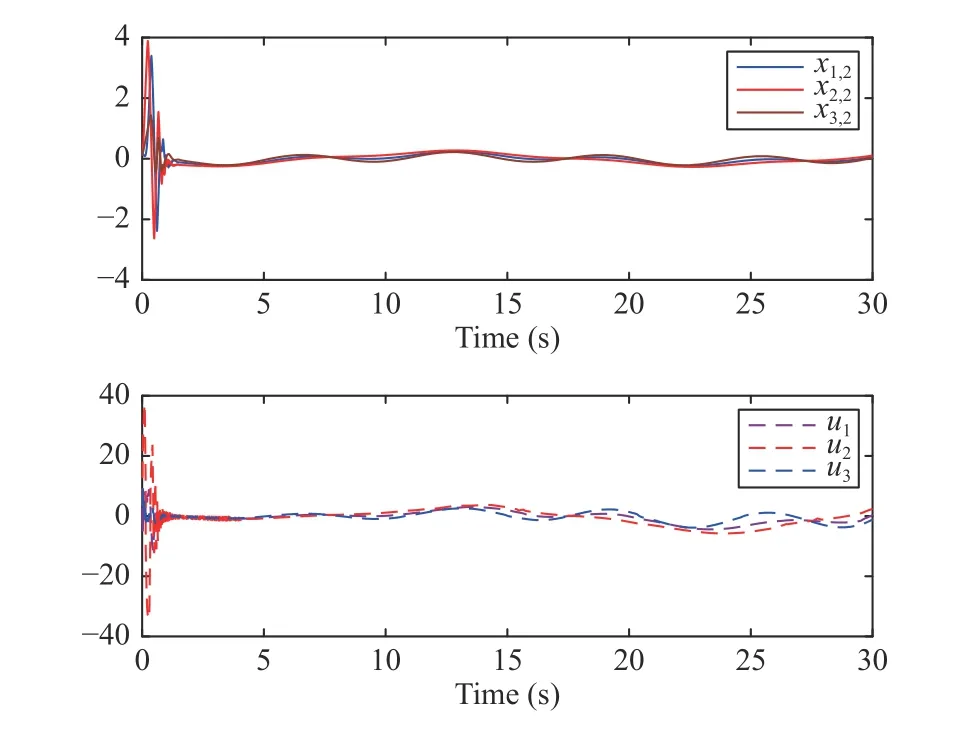
Fig. 5. The trajectories of control input signals ui.

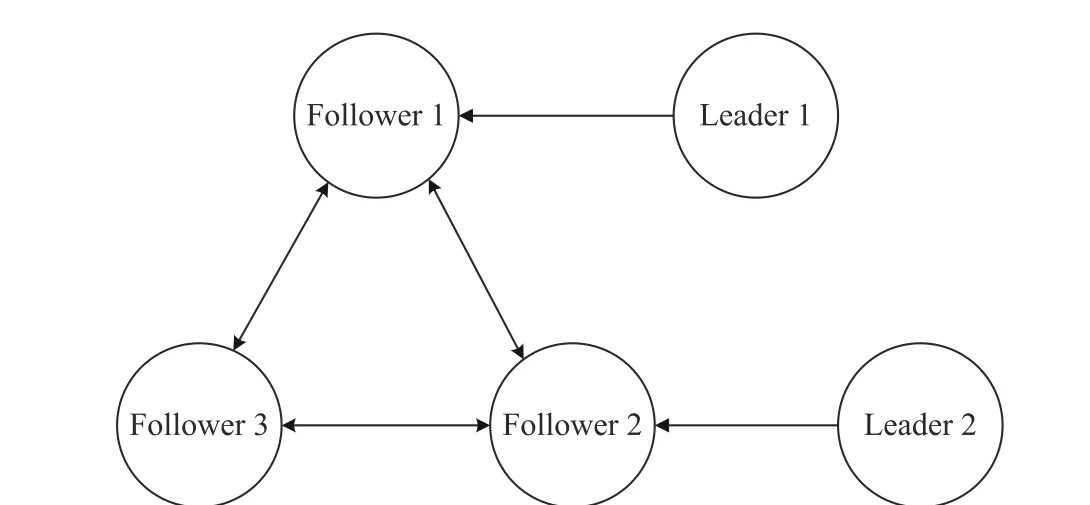
Fig. 6. Topology of the leaders and followers for Example 2.

The simulation results are given in Figs. 7-9. From Fig. 7，it can be seen that the output signals of the follower agent 1，agent 2， and agent 3 are driven to converge to the convex hull spanned by the two leaders. The systems’ statesxi，2and the control inputsuiare depicted in Fig. 8. The trajectories of the adaptive parameters are given in Fig. 9， in which the parameters ξ ˆi，jconverge to a constant. From Figs. 8 and 9， the conclusion that the signals in the controlled system can be derived.

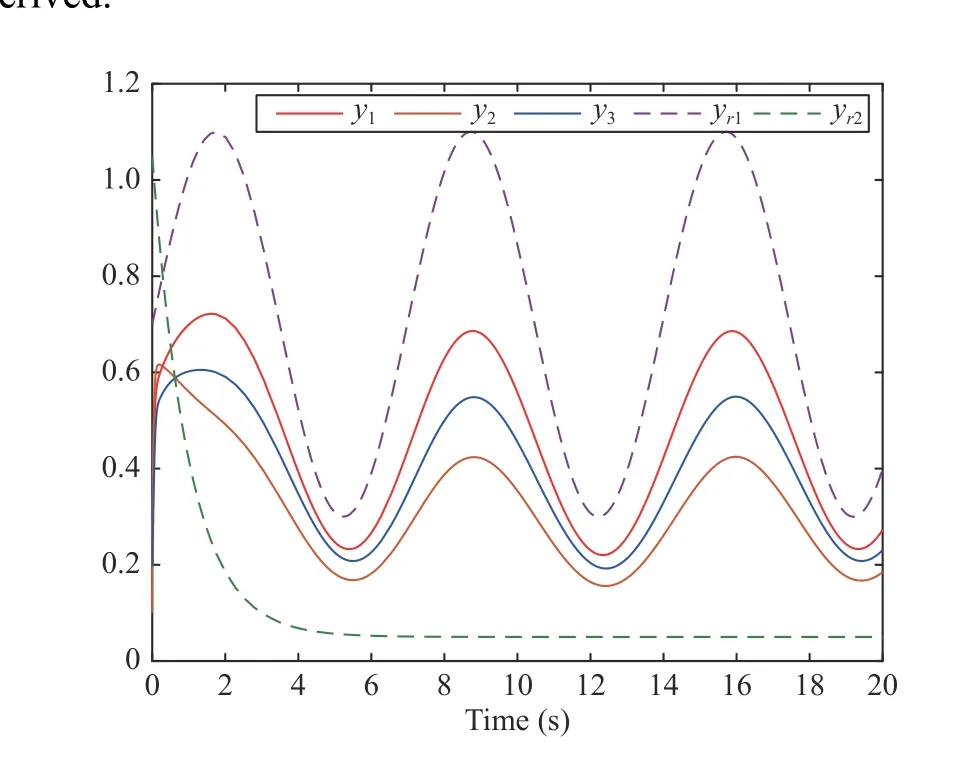
Fig. 7. The performance of containment control.

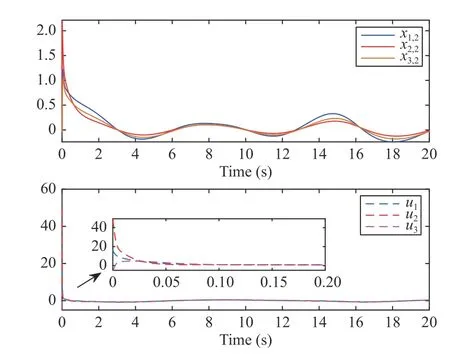
Fig. 8. The trajectories of the systems’ states xi，2 and the control inputs ui.

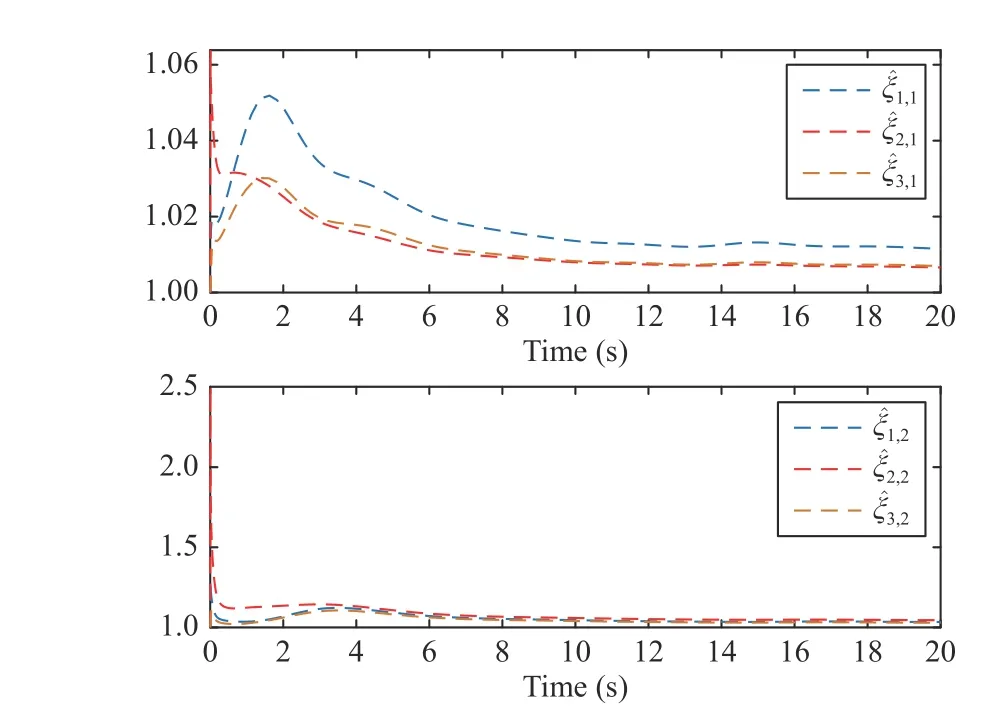
Fig. 9. The trajectories of the adaptive parameters updating.

To further verify the effectiveness of our proposed control algorithm， a practical example is provided， in which the class single-machine-infinite bus power system is considered the follower agent. The structure of this system is given in Fig. 10.The communication topology is defined as the same as that in Example 1.

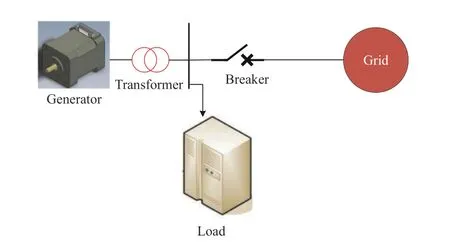
Fig. 10. Structure diagram of the single-machine-infinite bus power system.

Example 3:Consider the networked FOMASs consisting of the single-machine-infinite bus power system as the followers，in which the dynamic of each follower agent is described as[44]:

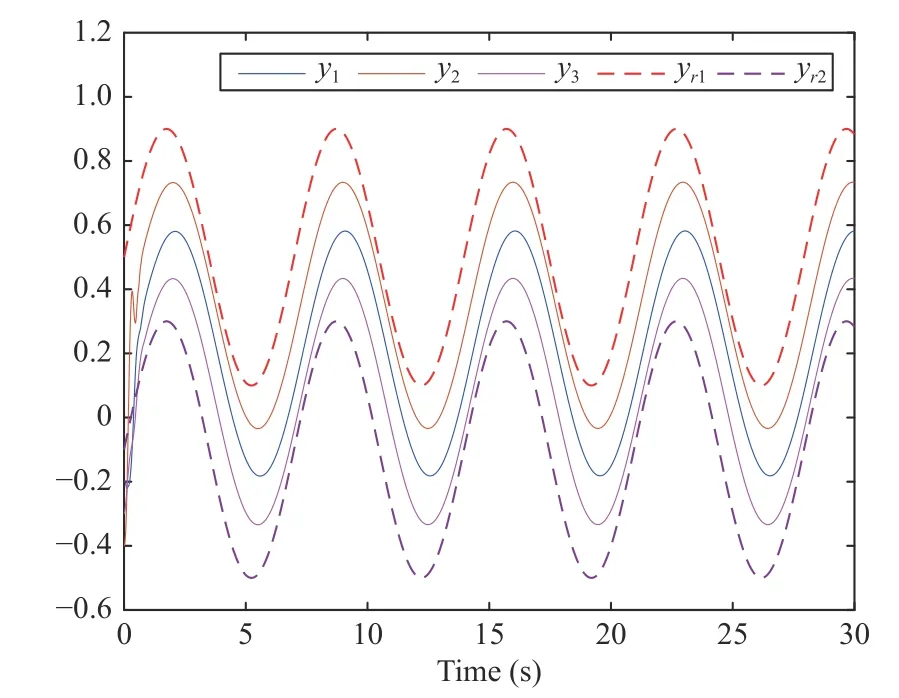
Fig. 11. The performance of containment control.

In order to further show the advantage of our proposed control method， the comparison of the containment errorei，1between the control method in [45] and that in this paper is given in Fig. 14. It can be seen that， under our proposed control scheme， the smaller containment errorsei，1are obtained.

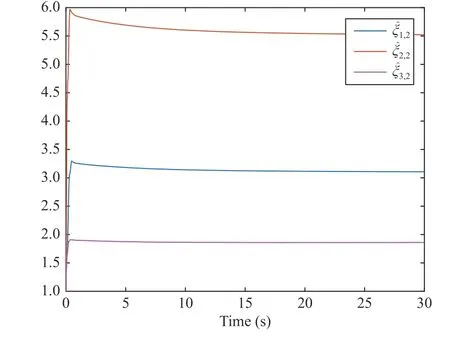
Fig. 12. The trajectories of the adaptive parameters ξ ˆi，2.

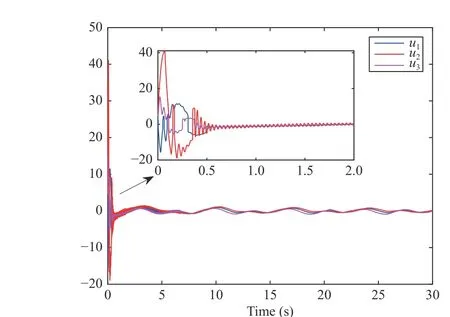
Fig. 13. The trajectories of control input ui.

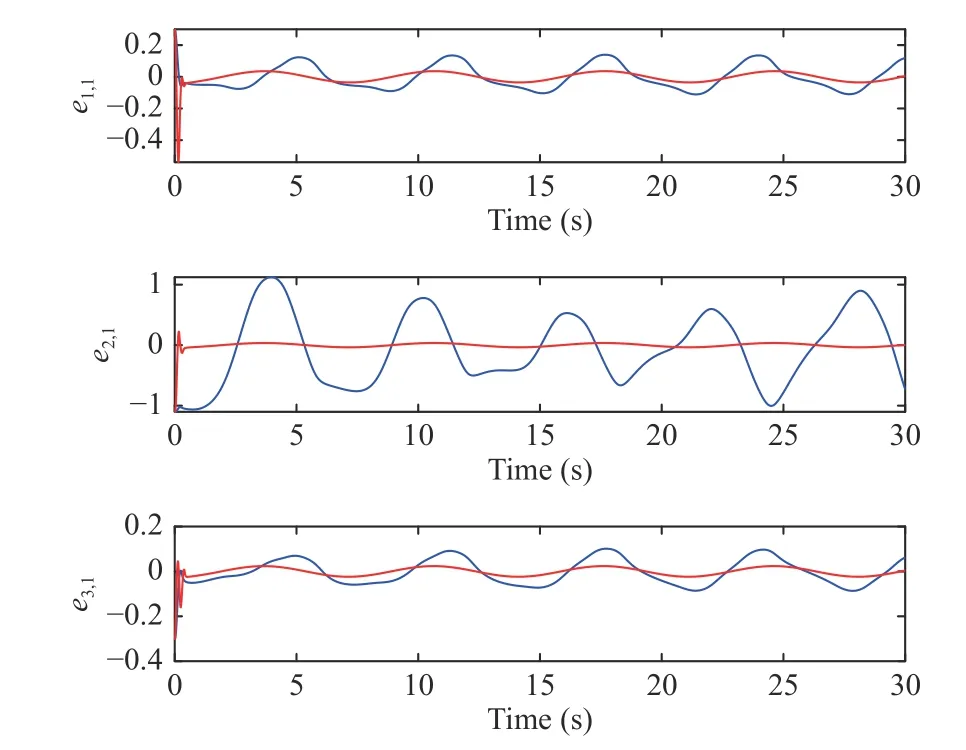
Fig. 14. The comparison of the containment error ei，1 between the control method in [45] (blue line) and our proposed control method (red line).

V. CONCLUSION

This paper has developed an adaptive distributed containment control for the FOMASs with time-varying parameters and disturbances. The bounded estimation approach has been applied to compensate for the effect of time-varying parameters and disturbances. By constructing a distributed error compensating scheme， a novel command filter backstepping has been developed， which can effectively compensate for filter errors and confirm the asymptotic convergence of the compensating signals. With the help of the extension of Barbalat’s lemma to fractional-order integrals，the asymptotic convergence of the containment errors is proven. In future works， more attractions will be attached to the bipartite containment and consensus control for the timevarying FOMASs with time-delay [46]–[48].