Hierarchical Cooperative Control of Connected Vehicles: From Heterogeneous Parameters to Heterogeneous Structures

Manjiang Hu， Lingkun Bu， Yougang Bian，，， Hongmao Qin， Ning Sun，Dongpu Cao， Senior，， and Zhihua Zhong

Abstract—As one of the typical applications of connected vehicles (CVs)， the vehicle platoon control technique has been proven to have the advantages of reducing emissions， improving traffic throughout and driving safety. In this paper， a unified hierarchical framework is designed for cooperative control of CVs with both heterogeneous model parameters and structures.By separating neighboring information interaction from local dynamics control， the proposed framework is designed to contain an upper-level observing layer and a lower-level tracking control layer， which helps address the heterogeneity in vehicle parameters and structures. Within the proposed framework， an observer is designed for following vehicles to observe the leading vehicle’s states using neighboring communication， while a tracking controller is designed to track the observed leading vehicle using local feedback control. Closed-loop stability in the absence and presence of communication time delay is analyzed， and the observer is further extended to a finite time convergent one to address string stability under general communication topology.Numerical simulation and field experiment verify the effectiveness of the proposed method.

I. INTRODUCTION

IN recent years， the connected vehicles (CVs) technique has been developed rapidly [1]. As one of the typical applications of CVs， vehicle platoon control has been widely studied， since it has great advantages on improving energy consumption and driving safety [2]， [3] and increasing traffic throughput [4].

Early vehicle platoon studies can be traced back to the PATH project carried out in 1980s [5]， [6]. Nowadays， the platoon control technique has been applied to many occasions[7]， e.g.， cooperative control of CVs in unsignalized intersection [8]. Recently， a new conceptual on-demand transportation application， called the intelligent vehicle stream (IVS) system，has been proposed in China. In this application， the advantage of the platoon control technique has been efficiently utilized.As shown in Fig. 1， the IVS system contains multiple CVs and a dedicated ring road. The CVs run in a platoon in the main lane and may enter or leave the platoon to pick up or drop off passengers under the charge of a vehicle scheduler. By using the platooning technique， the IVS system is more flexible than the subway system and may have better traffic throughput and lower travel delay.

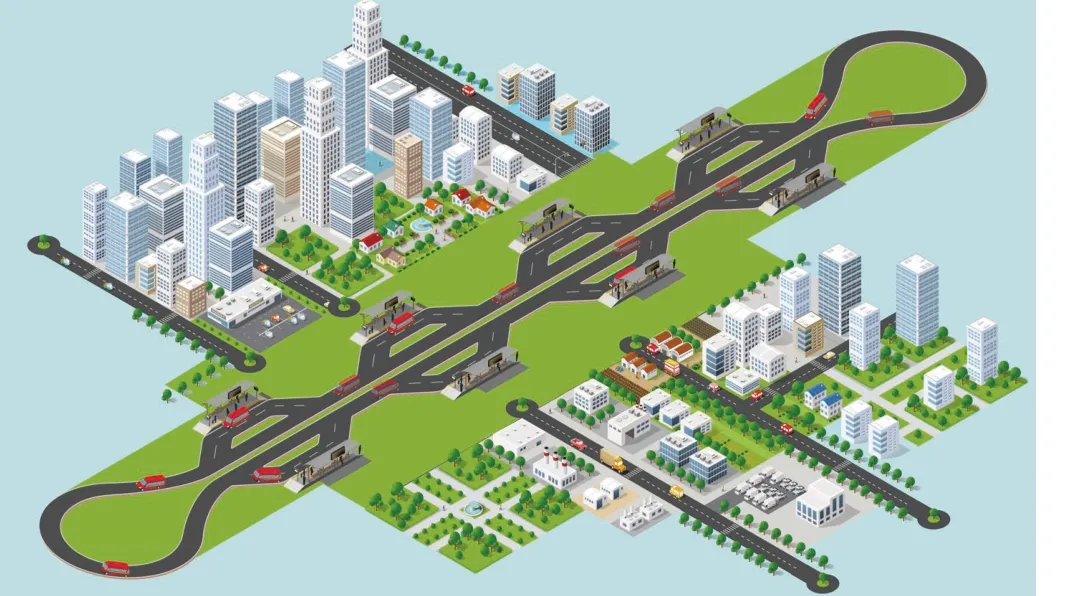
Fig. 1. Illustration of the intelligent vehicle stream system.

In vehicle platoon control， vehicle dynamics has a great influence on controller design. Considering a linear vehicle dynamics model， Zhenget al. [9] studied internal stability when all the eigenvalues of the information flow topology(IFT) matrix are real numbers based on eigenvalue decomposition and the Routh-Hurwitz criterion. Liet al. [10]extended [9] to the case where the IFT matrix has complex eigenvalues and designed a distributed controller with an exponential convergence rate. Differently from the homogeneous vehicle dynamics models mentioned above， Zhenget al.[11] considered heterogeneous parameter vehicle models in stability analysis by exploiting the lower triangular structure of directed acyclic graphs. Bianet al. [4] further extended [11]to the multiple predecessors following (MPF) topology to study the relationship between heterogeneous time headway，dynamics time lag， and control gains. Liet al. [12] proposed an adaptive learning law for heterogeneous multi-agent systems to deal with the unknown nonlinear dynamics. Based on the theory of partial differential equation， Ghasemiet al.[13] analyzed the internal stability of platoons with heterogeneous vehicles under the bidirectional topology. Besides， Liet al. [14] proposed a new car-following model considering the communication probability of the beacon transmission and designed a nonlinear consensus-based longitudinal control algorithm for vehicle platoon consensus control. This work was further extended to a distributed nonlinear consensus delay-dependent control algorithm in [15] for a CV platoon，which can ensure that vehicles smoothly reach the consensus state with respect to position and velocity. Yanget al. [16]designed a decentralized formation controller by adopting the“extension-decomposition-aggregation” process based on the formation stability conjecture， and formation stability was analyzed via a scalar Lyapunov function. Recently， some novel control methods and research directions have been proposed， e.g.， Zuet al. [17] studied multiple vehicle collision avoidance based on a distributed real-time trajectory planning algorithm; Gaoet al. [18] proposed a novel data-driven adaptive optimal approach for connected automated vehicle(CAVs) ensuring the asymptotic stability of the overall system; Gao and Jiang [19] proposed an improved global adaptive dynamic programming (ADP) algorithm which globally stabilizes nonlinear vehicle systems in an optimal sense for cooperative adaptive cruise control problem of CAVs; Chenet al. [20] proposed an economic adaptive cruise control (Eco-ACC) strategy based on action dependent heuristic dynamic programming for electric vehicles in a carfollowing scenario， and the proposed strategy does not rely on the domain knowledge of vehicle dynamics and can obtain the approximate optimal control effort under model-free conditions.

In a vehicle platoon， time delay in vehicle-to-vehicle (V2V)communication is inevitable and will affect the system performance greatly. To address this issue， Di Bernardoet al.[21] applied the Lyapunov-Razumikhin theorem to analyze distributed consensus strategy for vehicle platoon in the presence of heterogeneous communication delays. Wuet al.[22] designed a cooperative controller of multi-vehicle system affected by random communication time delay to ensure internal stability based onH∞methods. Ge and Orosz [23]designed an optimal control for platoon system considering both communication delay and driver reaction. Gaoet al. [24]applied robust control method to analyze heterogeneous vehicle platoon suffering from communication delay. Besides，Elahiet al. [25] addressed the design ofH∞consensus control for multi-agent systems under random packet dropout and communication delay.

As is generally known， small perturbations might be amplified and grow into a stop-and-go pattern， causing great loss of efficiency and high risks of accidents when string instability occurs. On the contrary， the platoon size is easily scalable and new vehicles can join the formation if string stability is guaranteed [26]. Therefore， string stability is of great significance， which describes the ability to attenuate errors. In terms of string stability， existing studies have proposed different definitions. Fenget al. [27] made a comprehensive summary of various string stability definitions and deeply analyzed the relationship， advantages， and disadvantages of each definition. The commonly used definition includes strong frequency domain string stability (SFSS) [28]and time-domain string stability (TSS) [29]. Seileret al.[30]concluded that the predecessor-following topology (PF) leads to string instability under linear feedback control， while the predecessor-leader-following topology (PLF) on the contrary.Bianet al.[4] analyzed the relationship between time headway and string stability of homogeneous vehicle platoon and obtained the lower bound of time headway using the SFSS definition. To get rid of the limitation of homogeneous time headway above， Ankem and Darbha [31] analyzed string stability of heterogeneous time headway using the homogeneous vehicle model， which requires time headway to decrease with the increase of vehicle index. The definition of SFSS is often used in homogeneous linear vehicle models， and the behavior of spacing errors as they propagate through a vehicle platoon can be characterized by a transfer function [4]， [30]，[31]. The norms of the transfer function above can determine the string stability from the perspective of energy， which makes deriving a unified analytical conclusion guaranteeing string stability easier. However， the string stability of heterogeneous vehicles is facing great challenges. The errors are related to heterogeneous dynamics， consisting of not only the self-vehicle’s dynamics， but also neighbor vehicles’.Furthermore， the heterogeneous dynamics of neighbor vehicles are greatly coupled through communication topology.The above leads to two great challenges: 1) the errors for heterogeneous vehicles platoon do not amplify or attenuate uniformly regardless of whether the system is string stable or not; 2) various communication topologies make it difficult to draw a unified analytical conclusion. Therefore， it is of great significance to find a definition for heterogeneous vehicle platoons that can not only ensure system performance， but also facilitate theoretical analysis， which will be discussed in Section V.

The idea of hierarchical control is widely used in the field of vehicle platoon control， but it has quite different meanings in terms of specific problems. Duretet al. [32] proposed a hierarchical decision and control framework for automated truck platoons to facilitate lane-changing maneuvers of surrounding vehicles near on-ramps and off-ramps. The tactical layer uses a first-order traffic flow model to generate decisions， while the operational layer uses a third-order longitudinal dynamics model to control truck accelerations.Chenet al. [33] designed a cooperative merging strategy for CAVs based on a hierarchical control approach， where a tactical controller and an operational layer controller work together to select gaps for the merging of on-ramp CAVs. Guo and Yue [34] designed a hierarchical controller which consists of a feedback linearization controller and a robustH∞controller to guarantee individual vehicle stability and string stability of the platoon. Izadiet al. [35] proposed a twolayered hierarchical structure for managing the fleet of vehicles during faulty conditions， i.e.， upper-level fault diagnosis and lower-level fault-tolerant decentralized receding horizon controllers. Although the hierarchical idea is applied in various fields in different ways， it still brings new solutions to the challenges mentioned below.

As mentioned above， the authentic vehicle dynamics model can effectively improve the performance of the system.However， different vehicle dynamics models may determine which analysis method of the system to select [4]， [9]–[11].For instance， in [9]， a linear state feedback controller was designed for the linear homogeneous vehicle dynamics model.The whole system was written as a state space description through the Kronecker product， and then the large-scale system was decoupled into several sub-systems through eigenvalue decomposition. This method required that the eigenvalues of the IFT matrix were all positive real numbers. Based on [9]， [10] extended the IFT matrix with real positive eigenvalues to a general matrix， and then decoupled the system matrix into subsystems with matrix complex eigenvalue decomposition. However， [10] still focused on linear homogeneous vehicle dynamics models [11] considered the parametric heterogeneity of vehicle dynamics and derived the system characteristic equation by determinant transformation method instead of eigenvalue decomposition used in [9] and [10].Reference [4] adopted the same method as [11] and obtained similar conclusions. Differently， [11] was suitable for the directed acyclic IFT， while [4] was suitable for the multiplepredecessor following topology.

In summary， most of the existing studies mentioned above are based on a third-order vehicle model with a homogeneous or heterogeneous time lag in acceleration response (e.g.， [4]，[9]–[11]， [24]). In this case， the platooning vehicles accept desired acceleration inputs and share a homogeneous model structure but heterogeneous model parameters. However， in practice， the dimensions or the internal structure of the matrix representing the dynamic state transition is quite different due to the different characteristics of vehicle dynamics. For example， some vehicles may have a desired-velocity control mode， i.e.， they only accept desired velocity input， especially when designing a platoon controller for modified product vehicles [36]， [37]. In this case， the platooning vehicles suffer from not only heterogeneous model parameters but also heterogeneous model structures. These systems’ state equations cannot be written by the Kronecker product; moreover，multiple heterogeneous vehicles will be coupled due to the various IFT. It is difficult to decouple by using matrix transformation or eigenvalue decomposition used in the existing literature， let alone drawing a unified conclusion. Moreover，we take the communication delay into account， which also brings greater complexity. Therefore， it will bring great challenges to platoon controller design and system analysis，which requires a new approach to solve the current challenges.

Fortunately， the hierarchical idea above brings us new enlightenment. To solve the problem mentioned above， this paper designs a unified hierarchical framework for platoon control of CVs with both heterogeneous model parameters and structures. Some preliminary work has been reported in [38].The contribution of this paper is as follows:

1) A unified hierarchical framework consisting of an observing and a tracking layer is proposed for platoon control of connected vehicles with both heterogeneous model structures and parameters for the first time. This framework separates neighboring information interaction from local dynamics control， which helps address the parameter and structure heterogeneity in vehicle dynamics. This method extends the study of model parameter heterogeneity [4]， [11]，[39] to the case of both heterogeneous model parameters and structures， which increases the application range of the proposed method.

2) Within the proposed framework， the necessary and sufficient conditions for the time delay-free system stability are derived by using the Routh-Hurwitz criterion. Further， the stability condition in [38] is extended to account for communication time delay， and the upper bound of admissible communication time delay is derived， which facilitates controller implementation in real applications.

3) To account for string stability， the upper-level observer is extended to a finite-time convergent one so that the observer error converges fast to facilitate string stability analysis. On this basis， the relative error transfer function is derived to guide the selection of controller gains. Compared with [4]，[21]， the proposed method provides an effective approach for string stability guarantee under more general IFT， which enlarges the range of feasible IFT in platoon control design.

The rest of this paper is arranged as follows. Section II presents the preparation work， which includes node dynamics，information flow topology， and platoon control objective.Section III presents the design of controller structure. In the Section IV， the observer and tracking errors are analyzed， and the necessary and sufficient conditions for the stability of the system in the presence of communication time delay are derived. Based on the finite time observer， the sufficient condition to guarantee string stability is given in Section V.Finally， numerical simulation and field experiment verify the effectiveness of the proposed theory in Section VI and the last Section VII concludes the whole paper.

Notations:Denote by R and R+the sets of real numbers and positive real numbers， respectively， and byINanNdimensional identity matrix. Denote by λi(A) the eigenvalues of matrixA， and by R e(m) the real part of a complex numberm. Denote by d iag{r1，...，rN} a diagonal matrix with diagonal elementsr1，...，rN. For any positive integerN， define F={1，2，...，N}. Denote by Nithe neighbor set of vehiclei.Denote by ⊗ the Kronecker product. Denote by ||·||∞the infinite norm. And sign(·) denotes sign function. Define(·)[α]=sign(·)×|·|α.

II. PLATOON SYSTEM MODELING

Consider a vehicle platoon consisting of 1 leading vehicle andNfollowing vehicles indexed from 0 toN， consecutively.In this section， the dynamics models of the leading vehicle and following vehicles are introduced firstly， then the IFT is described using the graph theory， and platoon control objective is presented.

A. Dynamics of the Leading Vehicle

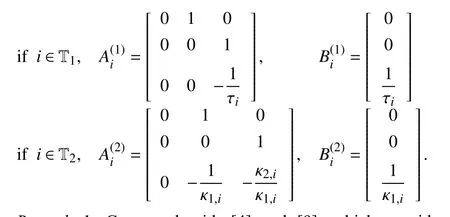
B. Dynamics of the Following Vehicles

Remark 1:Compared with [4] and [9]， which consider vehicles with homogeneous and heterogeneous parameters，model (5) considers vehicles with not only heterogeneous parameters but also heterogeneous structures. This poses challenges for the design and analysis of heterogeneous vehicle platoons.

C. Communication Topology

D. Platoon Control Objective

III. HIERARCHICAL PLATOON CONTROLLER DESIGN

In this section， we propose a hierarchical controller for platoon control of vehicles with heterogeneous parameters and structures. As shown in Fig. 2， the hierarchical control framework consists of an upper-level observing layer and a lower-level tracking layer. Correspondingly， each following vehicle has an upper-level observer and a lower-level tracking controller. Within this framework， their function and design are as follows:

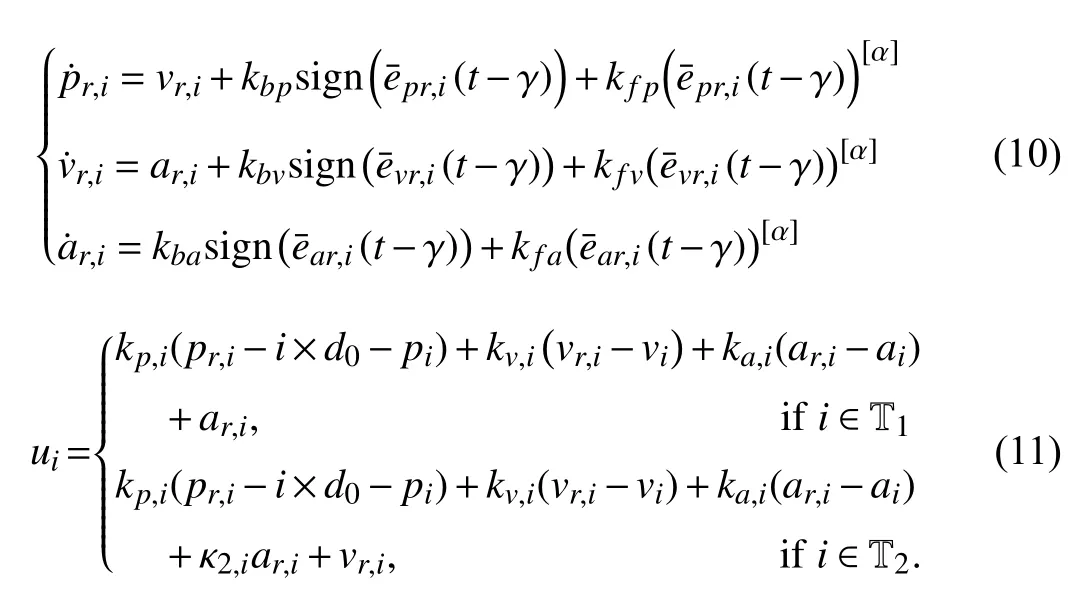
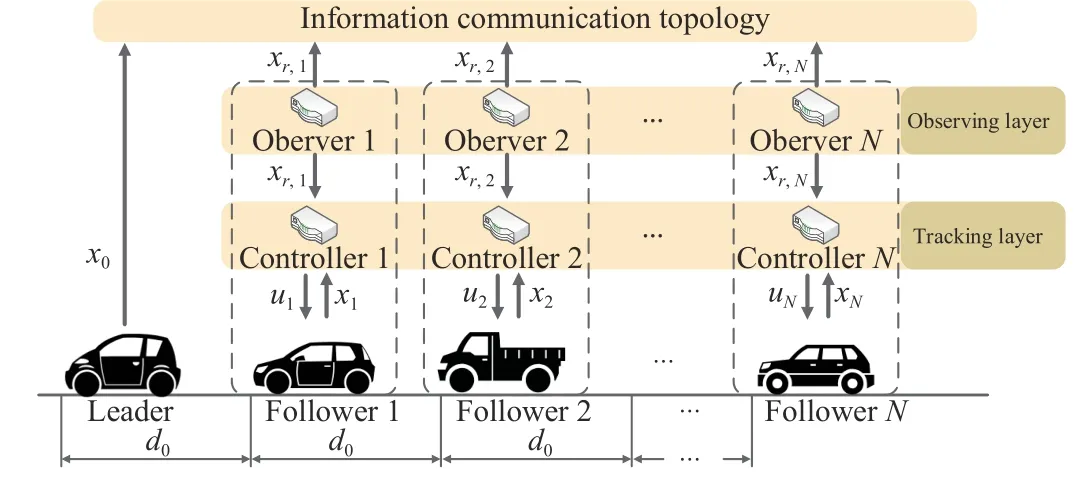
Fig. 2. Framework of the hierarchical platoon controller [40].

A. Upper-Level Observer Design

B. Lower-Level Tracking Controller Design

Remark 2:Differently from the existing platoon controllers for CVs with heterogeneous model parameters [4]， [11]， [39]，the proposed method separates neighboring information interaction from local dynamics control. In detail， the upperlevel observer uses neighbor information to generate local reference signals， while the lower-level controller uses the local reference signal for tracking control. The proposed unified framework simplifies the design process for heterogeneous vehicle platoons since one does not need to consider the communication topology during tracking controller design.

Remark 3:Differently from the widely used pure feedback controllers [4]， [11] for CVs with heterogeneous model parameters， the tracking controller (11) considers both feedforward and feedback， so that the following vehicles can achieve asymptotically tracking even if the leading vehicle moves with a non-zero acceleration (see Sections IV and V).

Remark 4:The proposed controller (11) is designed for cooperative control of 2 types of CVs. In practice， in the case of multiple types of CVs， the proposed method can still be used as long as there exist matrices Γiand Πisuch that regulator equation (12) holds forA0，Ai，Bi.

IV. SYSTEM STABILITY ANALYSIS

This section analyzes the stability of the hierarchical platoon controller in the presence of communication delay. The observing error is deduced first， after which the tracking error and system lumped error are then analyzed. Finally， the stability criterion of the system is presented.

A. System Error Analysis

B. Asymptotic Stability Criterion in the Absence of Time Delay

First， we consider the case of zero communication time delay. We directly present the following system stability theorem， which has been given in one of our previous work[38].

C. Asymptotic Stability Criterion in the Presence of Time Delay

Next， we consider the impact of communication time delay.Based on the above analysis， we firstly present a lemma on system stability with time delay， and then the asymptotic stability criterion for the proposed hierarchical platoon controller is provided.

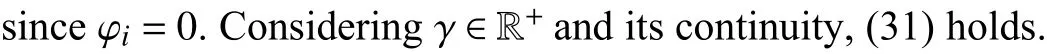
According to Corollary 1， the upper bound of the maximum feasible communication time delay is enlarged by 3/2 times，which helps increase the robustness of the proposed controller to unreliable V2V communication.

In fact， the range of observer and controller gains given in Theorems 1 and 2 only guarantees that the observing and tracking errors can asymptotically converge to 0. In practical applications， the gains should be carefully adjusted to balance the convergence rate and vehicle performance.

String stability is an important performance index in the field of vehicle platoon control. However， as mentioned above， the definition of homogeneous string stability in frequency domain is difficult to be applied to heterogeneous platoons. In addition， Shaw and Hedrick [26] presented that the errors can depend on the position of the vehicles within the platoon and it is not obvious if the errors will reach a limit，or keep growing larger as the platoon length increases.Fortunately， the definition of TSS can address the issues above and the challenges raised in Introduction.

Definition 1 [27]:The heterogeneous vehicle platoon has time-domain string stability (TSS) if given any ϵ ＞0， there exists a δ ＞0 such that sup|xi(0)|＜δ ⇒sup||xi(t)||∞＜ϵ for alli.

We know that the tracking errors are related to not only the self-vehicle dynamics but also the observation errors， which is further related to the dynamics of neighbor vehicles due to the coupling of communication topology. However， various communication topologies make it difficult to draw a unified analytical conclusion for string stability criterion. Therefore，we firstly extend the asymptotically convergent observer designed above to a finite-time convergent one which can get rid of the communication topology’s limitation and weaken the coupling relationship within neighbor vehicles， and then present a string stability criterion when the observing errors converge to zero.

A. Finite Time Observer

V. STRING STABILITY ANALYSIS

B. String Stability Criterion

Based on the above finite-time observer， the observation converges to the true value of the leader state afterT. Hence，the information topology is simplified to the leader following(LF) topology， which has been studied in [26]. Then according to the heterogeneous vehicle string stability definition provided in [26]， we derive the criterion of string stability by extending [26] from heterogeneous parameters to heterogeneous structures.

In the section， numerical simulation and field experiment are carried out to verify the effectiveness of the proposed theorems.

We consider a platoon consisting of 1 leading vehicle and 7 following vehicles， as is shown in Fig. 3. Obviously， its communication topology satisfies Assumption 1. The vehicle types and dynamic parameters are given in Table I where vehicle dynamics parameters are modified from [37]. The observer and tracking controller gains shown in Table I are initially chosen according to the proposed criteria and then fine-tuned through trial and error. The leading vehicle’s initial states arep0(0)=0 m，v0(0)=0 m/s，a0(0)=0 m/s2and its velocity profile is given in (40). The following vehicles’ initial states arepi(0)=-i×d0m ，vi(0)=0 m/s，ai(0)=0 m/s2，i∈F:

VI. NUMERICAL SIMULATION AND FIELD EXPERIMENT

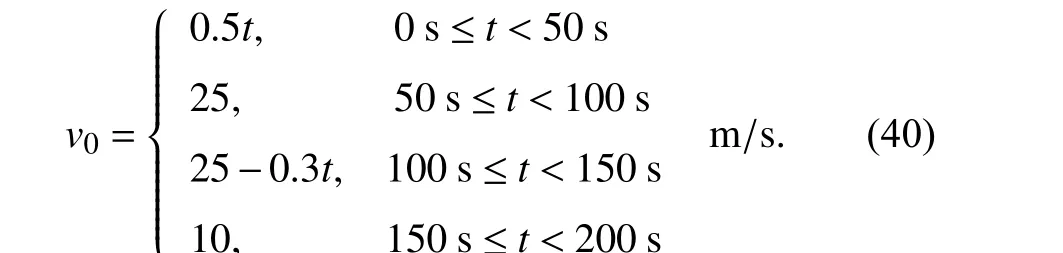
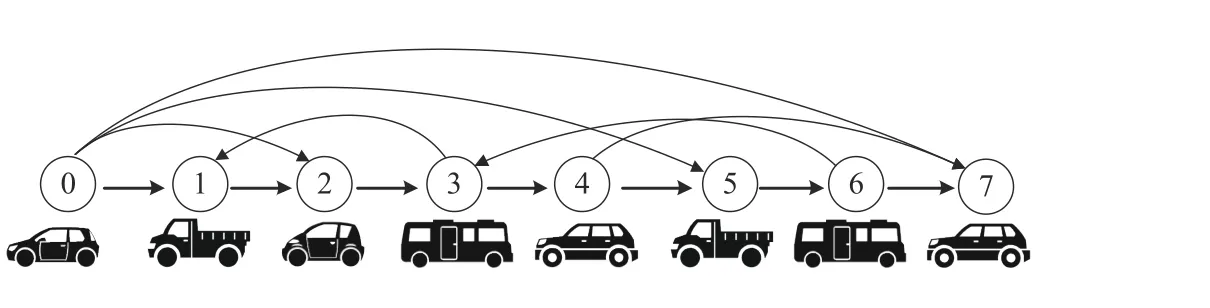
Fig. 3. Communication topology of the vehicle platoon.

A. Numerical Validation of System Stability

In this simulation， we validate system stability by using the asymptotically convergent observer. Two different control models corresponding to (10) and (11) are built in Matlab/Simulink to address the structural and parametric heterogeneity of vehicle dynamics. We assume that the upper bound of communication time delay is γ*=0.5 s， and we use random time delay to better validate the robustness of the proposed controller. In addition， a disturbance of velocitye-1.5(t-25)sin(3t)[45] is applied to the leading vehicle att=25 s， and a same onee-1.5(t-75)sin(3t) is applied to the following vehicles att=75 s to account for external disturbance and parameter mismatches brought by inaccurate feedback linearization. Here we choosekf#=1.2 based on Theorem 2 noting that |λmax(LP)|=5.0457 in Fig. 3. Fig. 4 shows the simulation results.

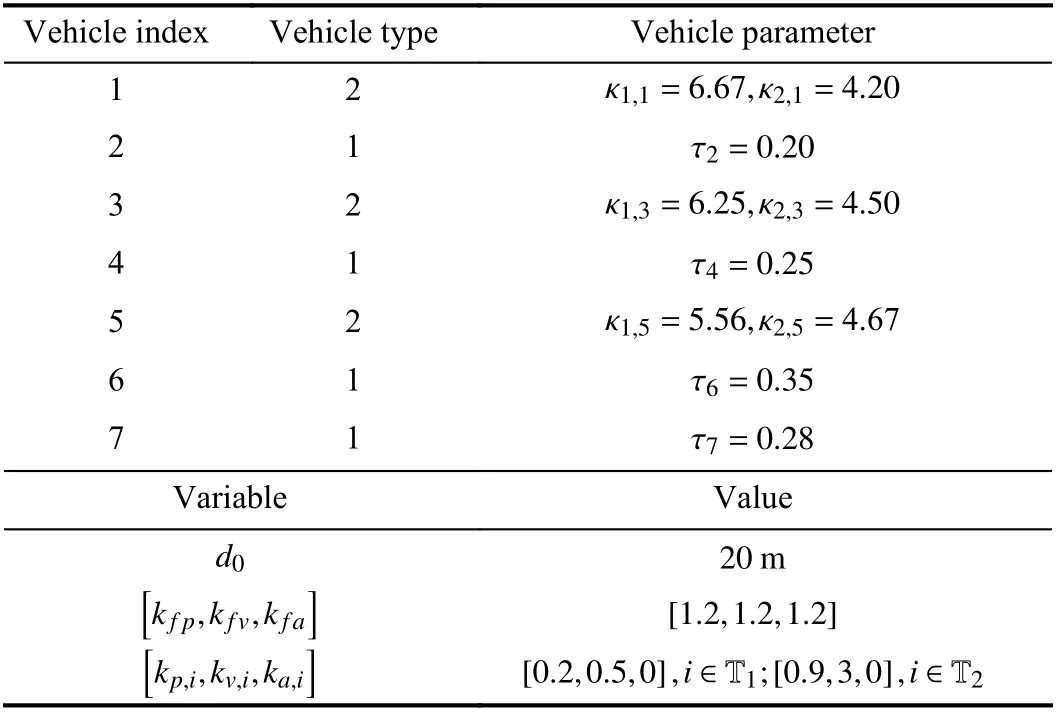
TABLE I SIMULATION PARAMETERS

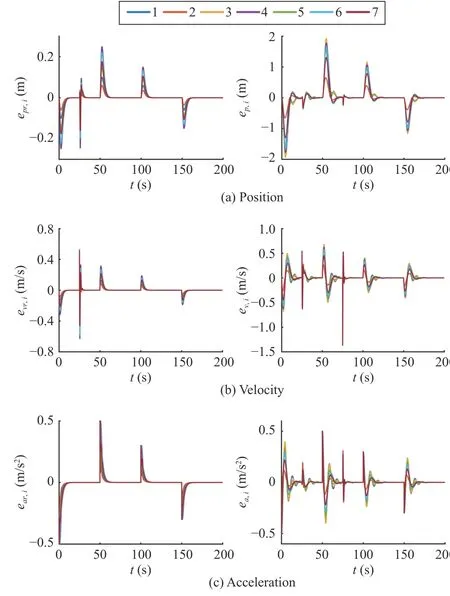
Fig. 4. Observing error and tracking error profiles with random communication time delay.

As Fig. 4 shows， the observing errors and tracking errors of the following vehicles asymptotically converge to zero when the leading vehicle finishes its acceleration and deceleration.Near 0 s， 50 s， 100 s， and 150 s， the observing errors and tracking errors change greatly because of the sudden change of the acceleration of the leading vehicle. At about 25 s， the observing errors of position and velocity fluctuate greatly since the leading vehicle suffers from imposed disturbance. At about 75 s， the tracking errors fluctuate greatly due to the external disturbance of the following vehicles. In addition， it can be seen that the observing errors are near 0 at 75 s， which indicates that the disturbance imposed on a single following vehicle will not affect the observing errors and the performance of the whole platoon system. This demonstrates the advantage of the proposed hierarchical control framework.The roughness of the vehicle state profiles is due to the randomness of communication time delay. Fig. 5 shows the control input of each following vehicle. Similarly， the larger variation of control input occurs near 0 s， 50 s， 100 s， and 200 s.In addition， control input less than 0 indicates braking for the vehicles that belonging to T1. These results confirm the validity of Theorem 1.

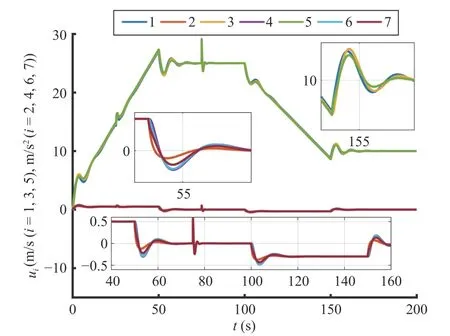
Fig. 5. Control inputs of following vehicles in the case of asymptotically convergent observer.

Remark 7:As shown in Fig. 4， since the proposed controller has an inherent feedforward and feedback format， the following vehicles can track the leading vehicle better than the methods in [4]， [11] that only consider state feedback.Meanwhile， compared with the robust control method in [46]that views model heterogeneity as a type of parameter uncertainty， the proposed method allows for heterogeneous feedback gain design to achieve more accurate tracking and faster convergence.

B. Numerical Validation of String Stability

In this simulation， we validate string stability by using finite-time convergent observer (32)， and the controller gainskb#，kf#(#=p，v，a)are selected according to (33). The platoon and parameter settings of the experiment in Section VI-A are still used. As shown in Fig. 6， the following vehicles’ finitetime observers generate local reference signals using the information from neighbor vehicles， which are almost identical with the true values of the leading vehicle state.Therefore， it is acceptable to simplify the general IFT to the LF topology.

Fig. 6. Local reference signals generated by the finite-time ovserver.

As Figs. 7(a)-7(c) show， the tracking errors of position，velocity， and acceleration asymptotically converge to 0.Moreover， Fig. 7(d) shows the propagation of relative errors.It is observed that the position tracking errors are attenuated along the platoon， which confirms the string stability.

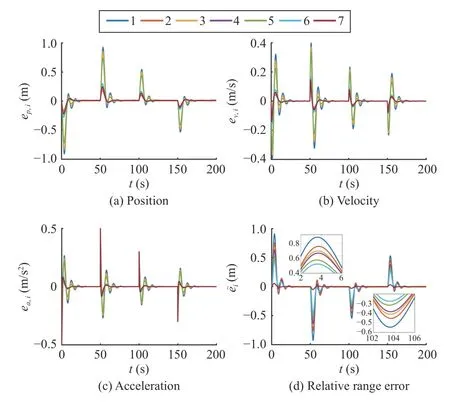
Fig. 7. Tracking control error and relative range error profiles.

C. Field Experiment Validation

Furthermore， field experiment is carried out on real test vehicles to validate the performance of the proposed method in applications， see Fig. 8. The bottom-layer control of the test vehicles has two control modes， i.e.， they accept either the desired velocity or the desired acceleration control modes，which naturally brings structural heterogeneity. Besides， the individual difference of the test vehicles in the motor，driveline， and tire modules directly brings parametric heterogeneity. The IFT in Fig. 3 is still used. The vehicles communicate with each other through WiFi， whose maximum communication time delay is 10 ms. The leading vehicle’s initial states arep0(0)=0 m ，v0(0)=0 m/s，a0(0)=0 m/s2and its velocity profile is given in (41). The following vehicles’ initial states arepi(0)=-i×d0m ，vi(0)=0 m/s，

ai(0)=0 m/s2，i∈F.

Fig. 8. Three vehicles used in the field experiment validation.

Since we only have 3 test vehicles， we conduct the experiment in four steps. 1) Before the experiment， the timevarying trajectory of the leading vehicle is pre-generated and stored locally in the 3 vehicles. In the next steps， the following vehicles read the leading vehicle’s information by accessing the local memory to simulate receiving the above information through wireless communication when they need it. 2) During the experiment， we first label the 3 vehicles with indices 1， 2，and 3， respectively. Then we carry out a platoon control experiment by using these vehicles， and their driving information over time， e.g.， their position， velocity， and acceleration， is saved locally for the ones which require obtaining it. It is noted that the 3 vehicles exchange information through wireless communication， and obtain the leading vehicle’s information by accessing local memory prestored in 1). 3) Then we re-label the 3 vehicles with indices 4，5， and 6， respectively， to continue the platoon control experiment， and these vehicles can use the stored information of vehicles 0， 1， 2， and 3 in chronological order for feedback control. 4) Finally， we conduct the experiment of the 7th vehicle in the same way. To identify the model parameter of the test vehicles， we use the system identification toolbox of MATLAB， as is done in [37]， and obtain the time lag parameters κ1，i，κ2，iin (4) and τi， shown in Table II.

TABLE II THE IDENTIFICATION OF THE TIME LAG PARAMETERS

Fig. 9 shows that the position error and velocity error change greatly when the leading vehicle changes its velocity abruptly at 0 s， 15 s and 30 s， and then asymptotically converge to 0. It can be seen from Fig. 9(b) that the velocity error fluctuates slightly， which is due to the factors such as road roughness and state measuring error. Fig. 10 shows the relative position errors between adjacent vehicles. It can be seen that the range error is uniformly bounded， which meets the requirement of heterogeneous string stability.

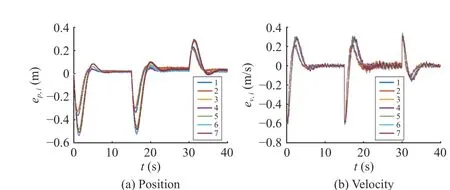
Fig. 9. Tracking error profiles in the field experiment.

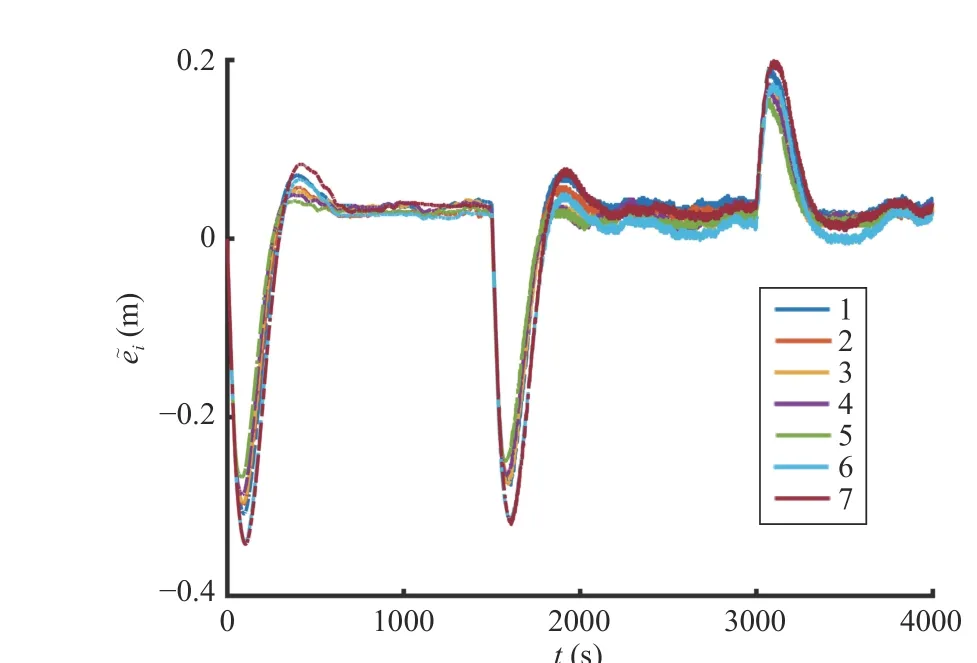
Fig. 10. Relative range error profiles in the field experiment.

The above results demonstrate the effectiveness of the proposed methods. We further would like to clarify that the proposed methods are also applicable to vehicle platoons with pure parametric heterogeneity since it provides a more general framework compared with the existing literature.

VII. CONCLUSION

This paper has studied platoon control of connected vehicles with heterogeneous parameters and structures suffering from communication time delay. A system stability criterion has been proposed on the range of control gains and the upper bound of communication time delay. Based on the finite-time observer technique， the transfer function of range error propagation has been derived for ensuring the string stability of the heterogeneous platoons. In the future work， communication package drops will be studied to further improve the robustness of the proposed method. Besides， in mixed traffic system， a fusion control strategy of human driving vehicles with consideration of driving style and CAVs may be carried out [47].

APPENDIX PROOF OF THEOREM 2

Proof:According to the two conditions of Lemma 1， the proof is divided into two steps.

Step 1:According to the proof of Theorem 1，Ac+Adis Hurwitz when (28) and (29) hold since the set given by (28)and (29) is a subset of (23) and (24). This satisfies the first condition in Lemma 1.