Adaptive Consensus Quantized Control for a Class of High-Order Nonlinear Multi-Agent Systems With Input Hysteresis and Full State Constraints
2022-09-08GuoqiangZhuHaoqiLiXiuyuZhangChenliangWangChunYiSuSeniorandJiangpingHuSenior
Guoqiang Zhu, Haoqi Li, Xiuyu Zhang,,, Chenliang Wang,,, Chun-Yi Su,Senior,, and Jiangping Hu, Senior,
Abstract—For a class of high-order nonlinear multi-agent systems with input hysteresis, an adaptive consensus outputfeedback quantized control scheme with full state constraints is investigated. The major properties of the proposed control scheme are: 1) According to the different hysteresis input characteristics of each agent in the multi-agent system, a hysteresis quantization inverse compensator is designed to eliminate the influence of hysteresis characteristics on the system while ensuring that the quantized signal maintains the desired value. 2) A barrier Lyapunov function is introduced for the first time in the hysteretic multi-agent system. By constructing state constraint control strategy for the hysteretic multi-agent system, it ensures that all the states of the system are always maintained within a predetermined range. 3) The designed adaptive consensus output-feedback quantization control scheme allows the hysteretic system to have unknown parameters and unknown disturbance, and ensures that the input signal transmitted between agents is the quantization value, and the introduced quantizer is implemented under the condition that only its sector bound property is required. The stability analysis has proved that all signals of the closed-loop are semi-globally uniformly bounded.The StarSim hardware-in-the-loop simulation certificates the effectiveness of the proposed adaptive quantized control scheme.
I. INTRODUCTION
WITH the rapid development of the concept of multiagent system in the control field, its far-reaching significance has caused the trend of the control scheme to change from a single system to a multi-agent system, which is also a hot topic in the research of control systems at present and even in the future. Moreover, the collaborative consensus control scheme derived from this emerging field has gradually stepped into the eyes of the scholars, that is, designing a kind of controller that can reasonably use the signals of each agent to make its output reach a consensus. Up to now, the consensus control based on multi-agent systems has achieved certain results [1]–[6], and more details can be found from the references.
However, the focus of the above research is on the first and second-order systems whose model details are known. In fact,in the control system, the uncertainty of the model is inevitable. As we all know, using adaptive control to handle systems with uncertain models has always been an enduring hot-spot issue in the control area [7]. Therefore, how to combine adaptive control and consensus control belonging to a multi-agent system has become a critical research item of multi-agent control. The combination of the above two methods is discussed in detail in [8]–[13]. With the passage of time, the control methods of high-order nonlinear multi-agent systems have gradually improved. Some controllers are designed based on state feedback [14]–[17], and some are based on output feedback [18]–[20]. Reference [19] further discussed the multi-agent system with unknown parameters.However, the proposed method requires a great number of data exchanges between agents, which may increase the communication burden to a certain extent. Reference [20] has a good solution to the communication burden problem in [19],and on this basis, the quantizer is elegantly introduced to further reduce the communication burden. Nevertheless, the high-gain K-filter proposed in [20] is not applicable to multiagent system with complex characteristics. None of the above references consider the state constraints, hysteresis, and other complex characteristics that the actual system may have. The research on the characteristics of the system itself needs to be supplemented.
In engineering application, it is often encountered that the actual model is limited by output or state [21]–[25], and the constraint set required for such situation can be considered as the safety state set of the actual system or the optimal operating state set of the engineered system. In order to deal with the system containing constraints, it is an admirable way to introduce a barrier Lyapunov function in the controller design process. In [24], the barrier Lyapunov function is introduced to the nonlinear pure feedback system with full state constraints to guarantee that the system does not violate the constraints. In [25], an adaptive controller with the barrier Lyapunov function is designed for SISO nonlinear systems with constraints and unknown control direction. All of the above studies are aimed at single system, but for multi-agent systems, the combination of barrier Lyapunov function and adaptive consensus control is an effective way to solve the state constraint problem. But so far, although there are many references for multi-agent systems with output constraints[26]–[29], the existing research on high-order nonlinear multiagent systems with full state constraints is very limited.Among them, [30] designs a consensus tracking controller for multi-agent systems with full state constraints, and uses the observers to measure the state of the system and the unmeasured state of the adjacent agent. However, this control strategy is not suitable for multi-agent systems with hysteresis nonlinearity or quantized input. It can be found that the research of high-order multi-agent systems with full state constraints needs to be further studied.
Hysteresis nonlinearity is a ubiquitous phenomenon in actual control systems, such as actuators of multi-machine power system [31], microgrid system [32] and mechanical system [33], where the presence of hysteresis nonlinearity may significantly reduce the execution efficiency of the actuator and eventually lead to oscillation or even instability of the control systems [34]–[37]. Hitherto, there are a lot of excellent research to solve the hysteresis phenomenon[38]–[41]. In the multi-agent system, the existence of hysteresis will not only greatly reduce the execution efficiency of the actuator, but also seriously reduce its performance. The Bouc-Wen differential model is one of the widely accepted hysteresis nonlinear models in mechanics, and it has been discussed in [42], [43]. In [43], the Bouc-Wen differential hysteresis model was described in detail, and an adaptive controller based on the inverse hysteresis model was constructed, which can eliminate the effect of hysteresis on a single system and achieve a good control effect. Reference[44] carried out further research on the basis of [43], and truly substituted the method of eliminating hysteresis into the multiagent system, and proposed a distributed adaptive outputfeedback consensus tracking control when the system has actuator hysteresis. In addition, there are few studies on such issues. Thus, it merits a deeper probe.
In the multi-agent system, which requires massive information exchanges, signal transmission is also one of the key points to be considered. When the number of agents increases, the burden of data communication will increase sharply. Not only that, the gradual increase in the number of modern digital devices has made it necessary for the signals of the actual system to be digitized before they pass through the communication channel. Therefore, quantizers have gradually attracted the interest of many scholars [45]–[50] as an effective means that can reduce the communication burden and discretize the signals. But it is worth noting that there are still vacancies in the quantized control of multi-agent systems.In [50]–[52], this vacancy is made up. By combining the quantized controller of single system proposed in [53]–[55]with high-order multi-agent systems, the control problem of quantizer in high-order multi-agent system is solved ingeniously. However, there is still a lot of research space for the quantitative control of multi-agent systems when it encounters full-state constraints and input hysteresis.
Aiming at a class of high-order nonlinear multi-agent systems with input hysteresis, this paper proposes an adaptive consensus quantization control strategy with full-state constraints, and has the following characteristics:
Firstly, in order to resolve the quantization hysteresis nonlinearity in multi-agent systems, inspired by [43], a hysteresis quantization inverse compensator is established,which not only eliminates the difficulty of input hysteresis for controller design, but also achieves the quantized control of the hysteretic multi-agent system.
Secondly, to cope with the state constraints of the system,the barrier Lyapunov functions are introduced into the hysteretic multi-agent system for the first time, by integrating this technology into the design process of the backstepping controller, all the states of the hysteretic system will not exceed the restriction conditions.
Finally, an output-feedback adaptive consensus state constraint quantized control algorithm is proposed for highorder nonlinear hysteretic multi-agent systems with unknown parameters and unknown disturbance. In addition, the realtime tracking control ability of the proposed control strategy is verified by HIL simulation.
The rest of the paper is organized as follows. In the Sec tion II, the model of multi-agent system is proposed and the preliminary knowledge is introduced. Sections III and IV,respectively carry out the design of the controller and stability analysis. Section V validates the effectiveness of the proposed control scheme through hardware-in-the-loop simulation.Finally, the conclusion is drawn in Section VI.
A. Algebraic Graph Theory
The topological structure of a set ofNnonlinear multiagents withn-order can be represented by an undirected graph G=(V,E), which consists of a set of node setV={1,...,N}and a set of edge set E ⊆V×V of the form (i,j), wherei≠j.It should be noted that if (i,j)∈E, it means thei-th andj-th agents can obtain mutual information during the signal exchange process. The adjacency matrixAwhich can represent the neighbors of each agent is defined as follows:
II. PROBLEM STATEMENT AND PRELIMINARIES
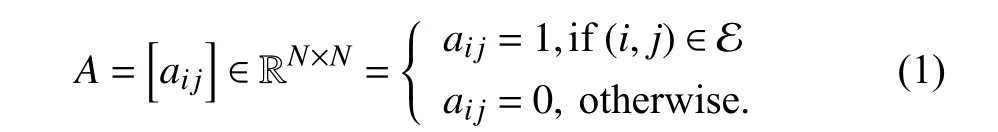


B. System Dynamic
The dynamics of thei-th agent in the following outputfeedback form is described by:

Remark 1:The high-order multi-agent dynamics (3) is an output feedback canonical form of nonlinear system which is widely used in literatures, e.g., [20], [56] and [57]. One feature of this model is that each agent has similar dynamic characteristics. In addition, the dynamic models investigated in [51] and [58] are switched high-order multi-agent systems,and each agent has its own switching signals and the switching time can be asynchronous, this model is suitable for under-actual mechanical system with weakly coupled. However, under certain conditions, the switched high-order multiagent system in [51] and [58] can be transformed into (3).
C. Hysteresis Quantization Inverse Compensator
In order to accurately describe the hysteresis nonlinearity in the system, inspired by [42], assume that the hysteresis quantization nonlinearity of each agent can be represented by a kind of Bouc-Wen hysteresis quantization model


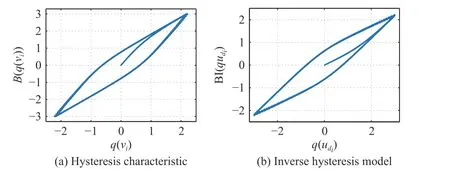
Fig. 1. Hysteresis quantization characteristic of i-th agent and its inverse compensator.

Fig. 2. Control signal transformation after hysteresis quantization inverse compensation.

Remark 2:The hysteresis quantization model defined in (4)is derived from the Bouc-Wen model [42] and improved,which not only retains the characteristic of the B-W model to express hysteresis nonlinearity well, but also takes the quantized input into account. It can be seen in subsequent simulations that the hysteresis quantization inverse compensator (7) proposed in this paper can be perfectly compatible with quantized input signal, and has better versatility than the traditional B-W inverse model [43], [44] in the face of hysteretic systems.
D. Quantizer

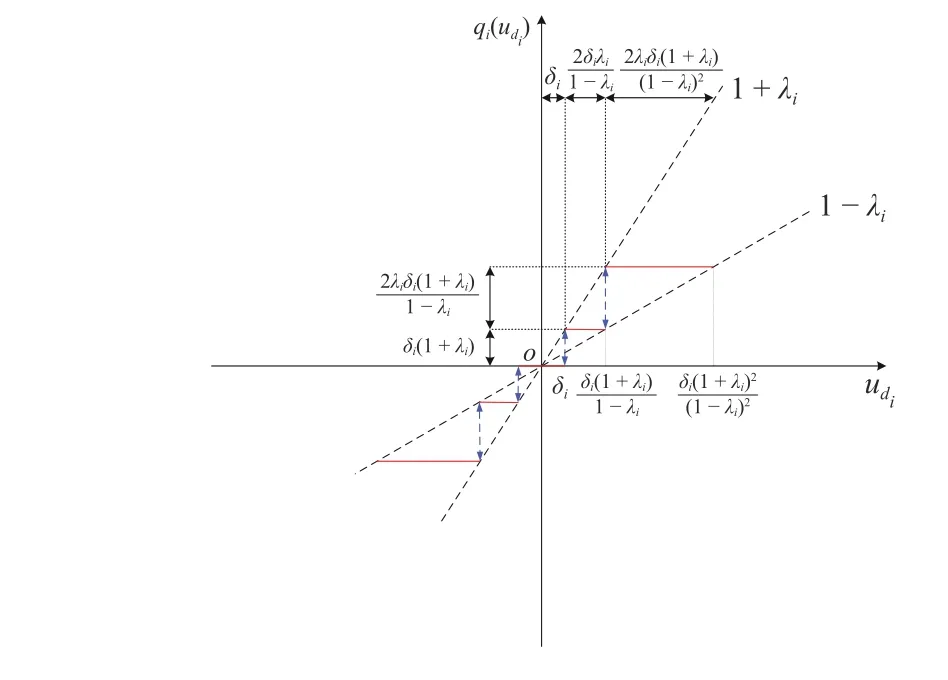
Fig. 3. Truncated logarithmic quantizer.
Remark 3:The sector bound property introduced in [54] can represent many typical quantizers, such as the two most popular quantizers: logarithmic quantizer and hysteresis quantizer [50], [51]. Both are currently the mainstream quantization methods. For the logarithmic quantizer, a certain fan-shaped bounded area can correspond to many quantizers with the same quantization density. For the hysteresis quantizer, which is composed of two quantizers with the same quantization density but different quantization values, it has more quantization levels but only one quantizer is working at the same time. The quantized value is “direct change” in the logarithmic quantizer, and “indirect change” in the hysteresis quantizer, that is, when the quantized value is converted from one value to another, the latter quantizer will have some dwell time before a new transition can be made.
Remark 4:Quantized control can effectively reduce the communication burden by quantifying the control signal,which is widely used [45], [46], [48], and actuator hysteresis nonlinearity is also common in practical physical systems[31], [32], [34]. In recent years, some outstanding works on quantized control for signal nonlinear system with actuator hysteresis have also been reported, such as [34], [35] and [36].It should be noted that a multi-agent system is composed of multiple single systems, so it is feasible to consider the input quantization and input hysteresis simultaneously in theoretical point of view. To our best knowledge, few relevant literature have been reported on the design of multi-agent control system by considering both input quantization and actuator hysteresis, therefore, the work of this paper is interesting. At the same time, the hysteresis phenomenon of actuator and the communication quantization problem between multi-agents also widely exist in actual physical system, so it is also very meaningful in the field of practical engineering application.
According to (9) and (10), the system (3) can be rewritten as

In this section, an adaptive consensus quantized control scheme with the barrier Lyapunov function is proposed for trajectory tracking control of high-order nonlinear multi-agent systems. Define the following barrier function:

III. THE PROCESS OF THE CONTROLLER DESIGN







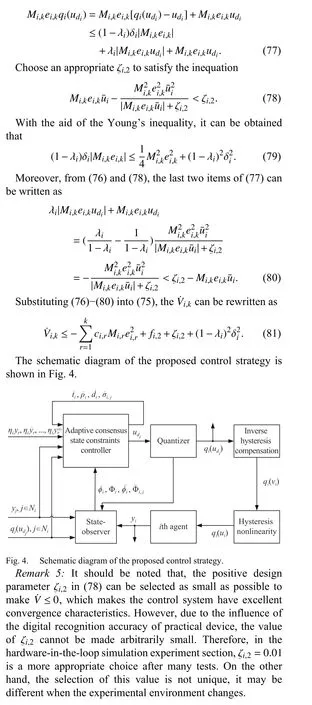
IV. STABILITY ANALYSIS
By synthesizing the above controller design procedure, the stability analysis of the whole closed-loop system can be summarized as the following Theorem, and the relevant theorem proving process is also given.

V. HARDWARE IN THE LOOP SIMULATION RESULTS
In this paper, the validity of the designed controller is verified on the Hardware-in-loop Testing Platform. The actual experimental environment is shown in Figs. 5 and 6, where the following modules are included:

Fig. 5. The experimental environment for simulation verification.
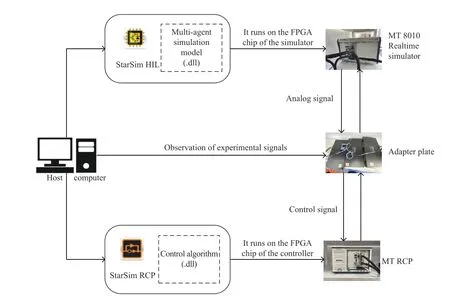
Fig. 6. The experimental system architecture.
NI PXIe-1071, the MT rapid control prototype (RCP), this experimental equipment with Kintex-7 325T FPGA @Xilinx,and 16 analog I/O channels with transmission rate of 1 MS/s.This device is utilized to verify the effectiveness of the proposed adaptive consensus quantized controller, and complete the real-time operation of the control code. Furthermore, the equipment used can also send the control signals to multi-agent model which is running on the MT Real-time simulator.
NI PXIe-1082, MT real-time simulator (RTS) with Kintex-7 325T FPGA chip, 16 bits synchronized analog I/O has a data transfer rate of 1 MS/s. It supports FPGA simulation for the multi-agent systems. The simulator accepts the control signal and calculates the response of the multi-agent system in real time and outputs to the controller box. The RTS, RCP and the signal adapter board constitute a closed loop experimental system.
Adapter plate:It is used to realize the signal connection between the RCP and the RTS.
Host computer:Using the StarSim RCP software to download the controller algorithm and the Matlab/Simulink multi-agent system model into the RCP and Realtime simulator, respectively.
In this section, consider a group of multi-agents consisting of four single arm robot manipulators to verify the adaptive consensus quantized control scheme in this paper, and its dynamics equations [59] are

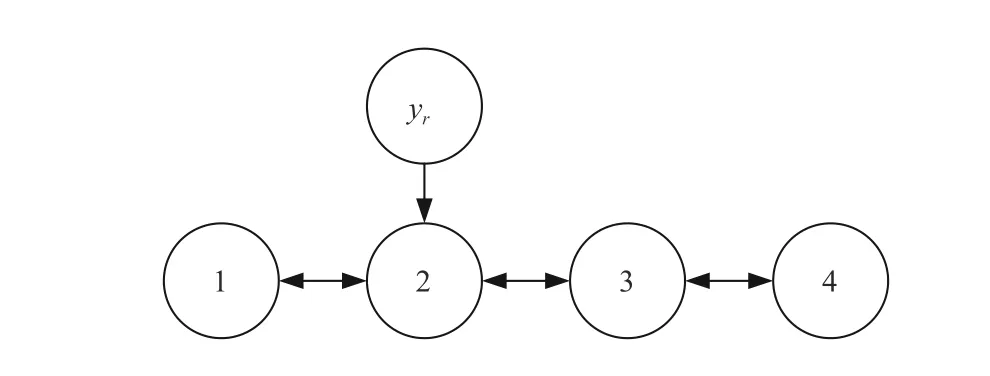
Fig. 7. Communication topology diagram for (82).



Fig. 8. The tracking trajectory of y r, yi, i=1,...,4.
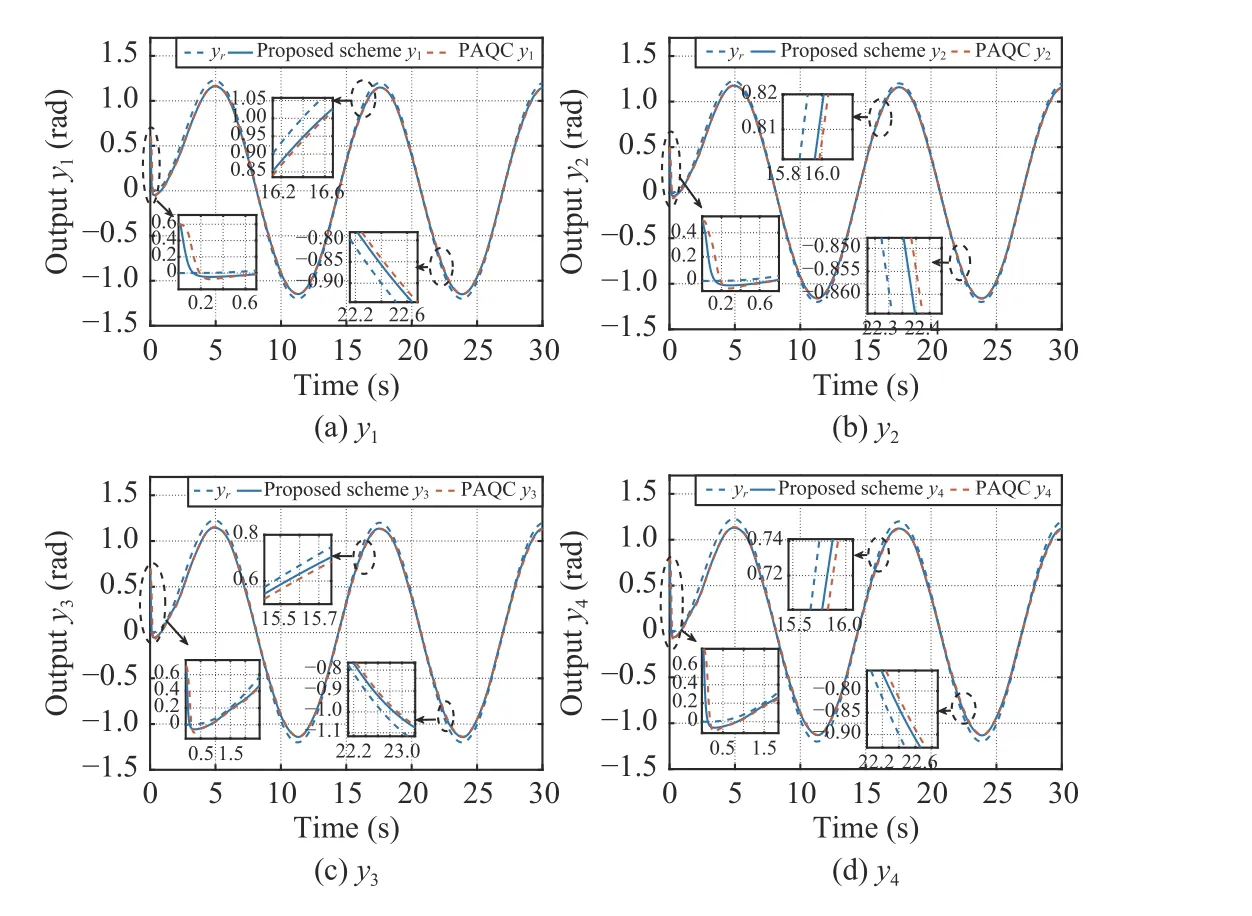
Fig. 9. Tracking performance comparison.
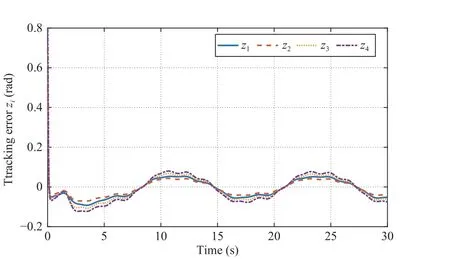
Fig. 10. The tracking error of z i, i=1,...,4.

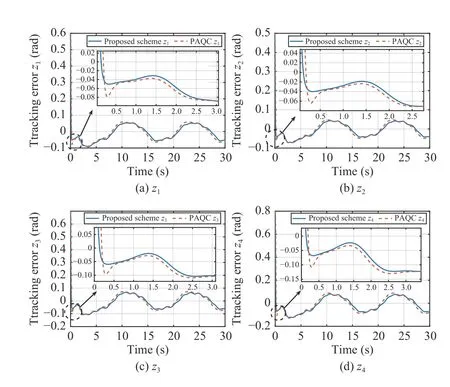
Fig. 11. Tracking error comparison.
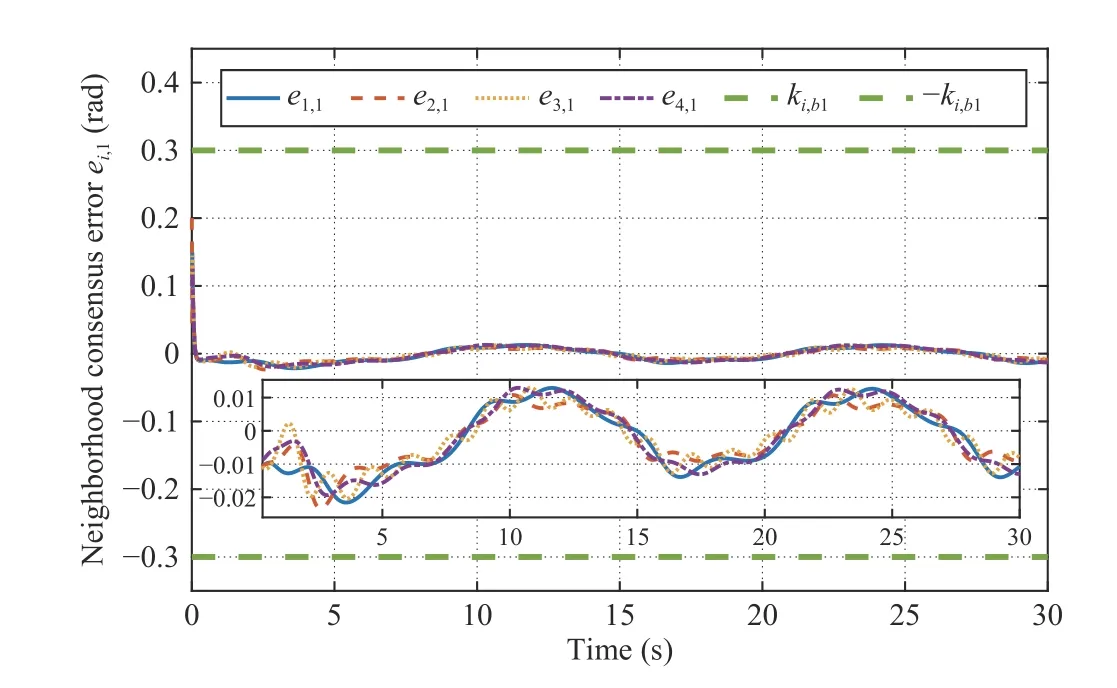
Fig. 12. Neighborhood consensus error e i,1, i=1,...,4.
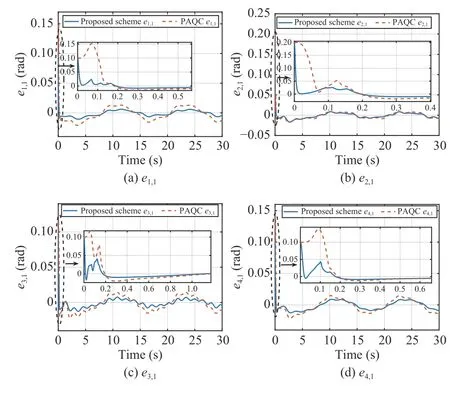
Fig. 13. Neighborhood consensus error comparison.
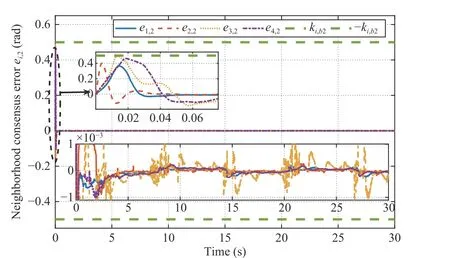
Fig. 14. The second error surface e i,2, i=1,...,4.
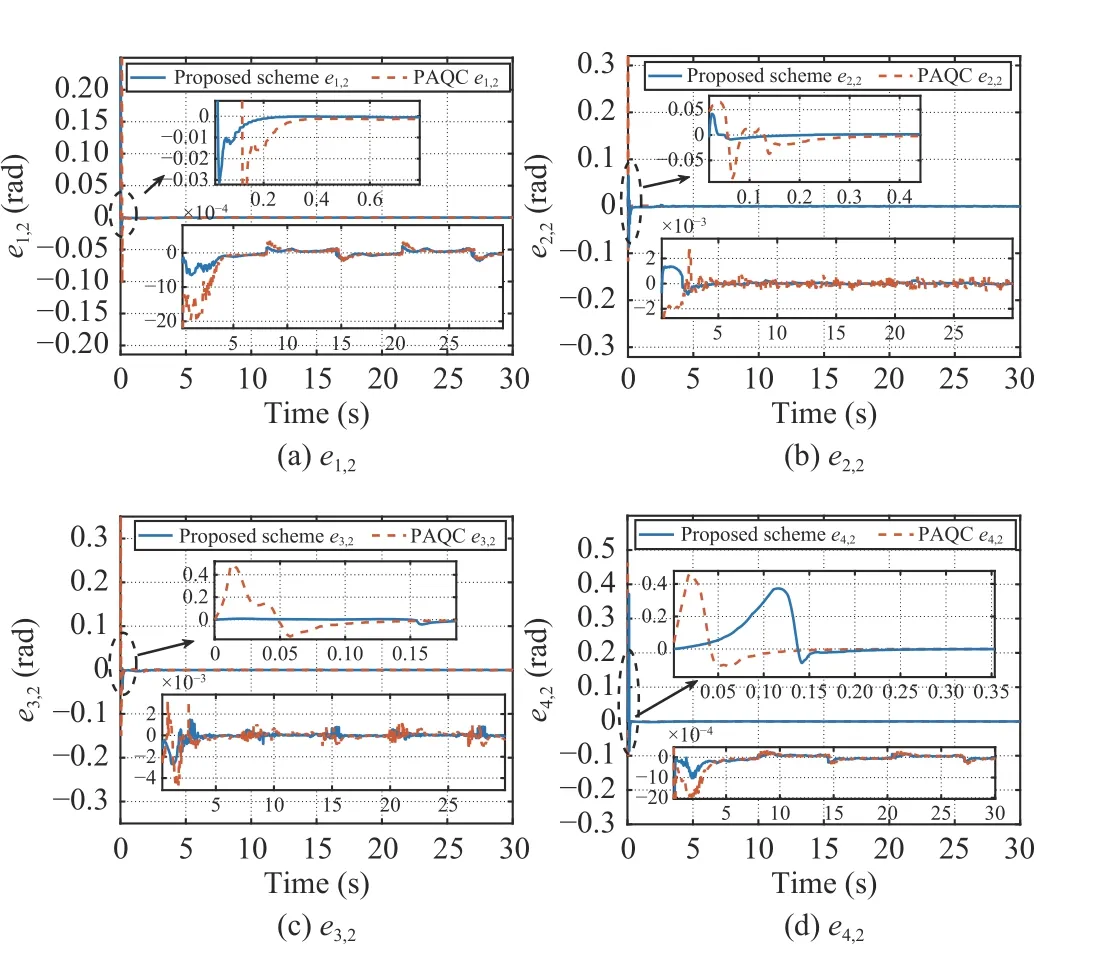
Fig. 15. The second error surface comparison.

Fig. 16. Desired input u d1, hysteresis compensation input v1 and actual input u1.

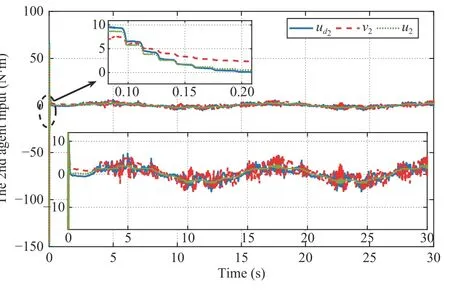
Fig. 17. Desired input ud2 , hysteresis compensation input v2 and actual input u2.

Fig. 18. Desired input ud3 , hysteresis compensation input v3 and actual input u3.
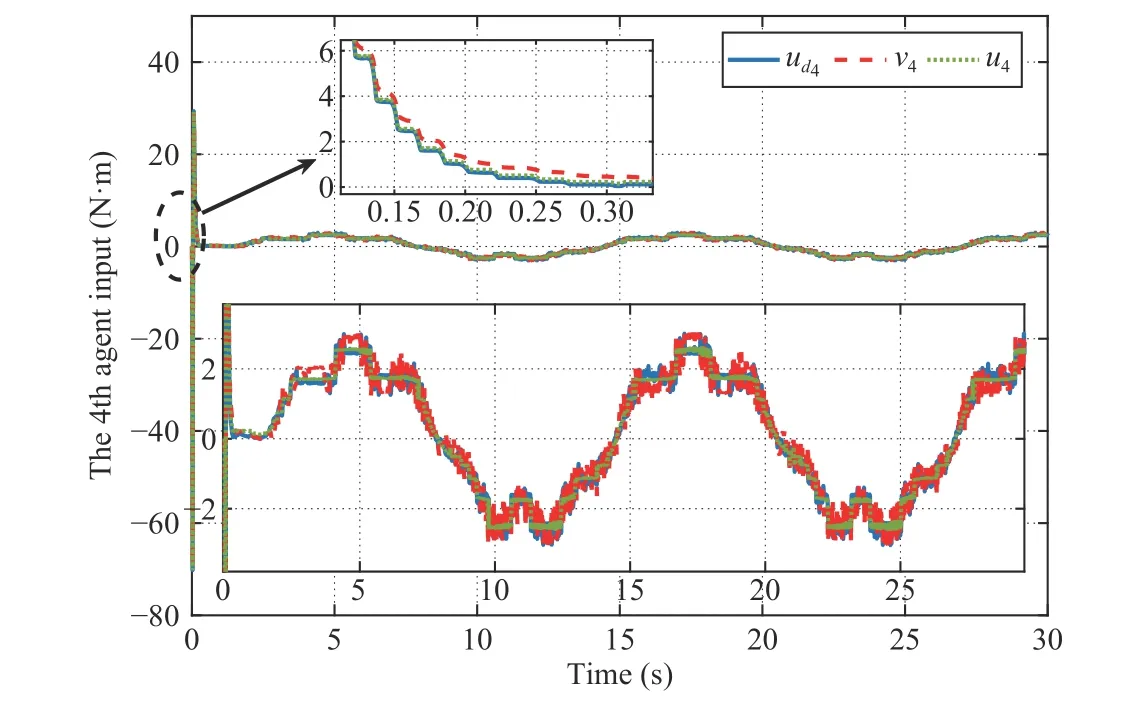
Fig. 19. Desired input ud4 , hysteresis compensation input v4 and actual input u4.
Remark 6:The design parameters of the proposed control strategy could be selected as follows:Step 1:The design parameters ζi,1and ζi,2should be as small as possible within the allowable range of the actual system according to (97) and(98);Step 2:Based on the property of high-gain K-filter [20]and (36), the value ofaicould be determined, and then, according to (99), the value ofεcould also be obtained;Step 3:Similarly to Step 2, by using (88) and (99), the remaining design parametersci,1, ...,ci,k, θdi, θσij, θρi, θℓi, βρi, βℓi, Γdi,Γσi jcould be selected.
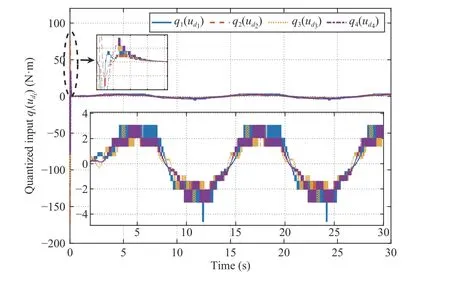
Fig. 20. Quantized input q i(udi), i=1,...,4.
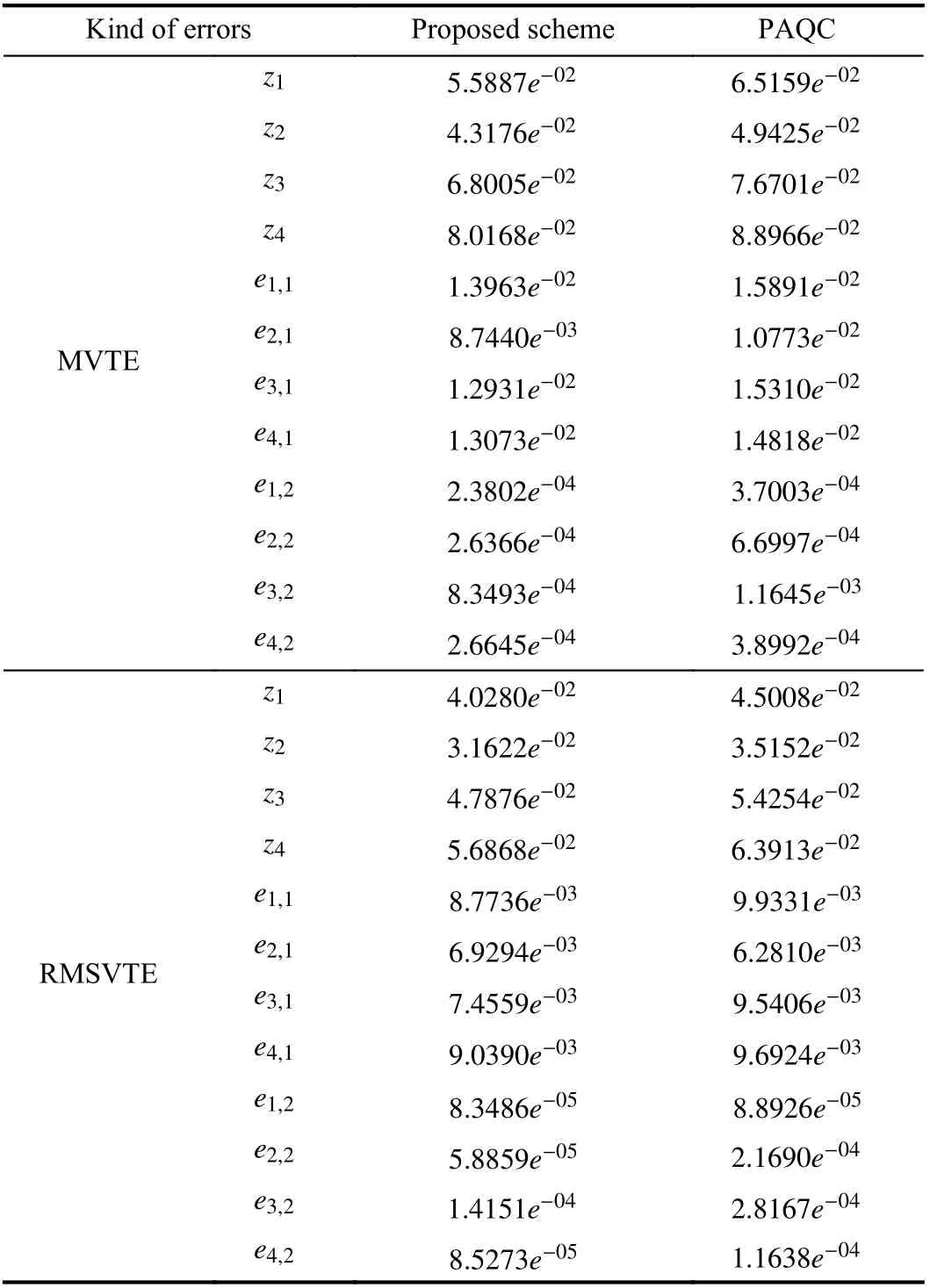
TABLE I THE MVTE AND RMSVTE
VI. CONCLUSION
An adaptive consensus quantization output feedback controller has been investigated for a class of high-order multi-agent systems with full state constraints and input hysteresis. By introducing the barrier Lyapunov function, the full state constraints problem of the nonlinear multi-agent systems is addressed. And a corresponding inverse hysteresis model is established for the hysteresis nonlinearity of each agent. Moreover, by designing a quantization controller, the communication burden of the system is greatly reduced. The effectiveness of the proposed control method has been experimentally verified on the Hardware-in-loop Testing Platform. It has been proved that all the signals in the closedloop system are semi-globally uniformly bounded.
APPENDIX PROOF OF THE THEOREM 1



杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Autonomous Maneuver Decisions via Transfer Learning Pigeon-Inspired Optimization for UCAVs in Dogfight Engagements
- Interval Type-2 Fuzzy Hierarchical Adaptive Cruise Following-Control for Intelligent Vehicles
- Efficient Exploration for Multi-Agent Reinforcement Learning via Transferable Successor Features
- Reinforcement Learning Behavioral Control for Nonlinear Autonomous System
- An Extended Convex Combination Approach for Quadratic L 2 Performance Analysis of Switched Uncertain Linear Systems
- Adaptive Attitude Control for a Coaxial Tilt-Rotor UAV via Immersion and Invariance Methodology
