基于多项式修正的LSTM网络流量预测

靳明飞

（合肥工业大学 安徽 宣城 242000）

0 引言

随着互联网的迅速发展，使用人群日益增加。同时，网络安全问题也越发复杂。网络流量是网络传输的关键因素，能更好地反映出网络系统的工作状态。许多常见的网络攻击流量特征十分明显。通过对网络流量预测与分析，使相关人员能更好地进行网络管理以及预防可能出现的网络攻击。

目前，国内针对网络流量预测方法大部分是基于规则、范例或基于数理统计等推理技术，如SVM、贝叶斯信念网络等。随着深度学习中循环神经网络的发展，其在网络故障检测中具有极大潜力，受到了学者们广泛关注和应用。

本文将利用不同结构的LSTM神经网络对流量数据进行特征提取，再利用多项式拟合的方法，并基于强化学习的思想，对不同的特征进行修正，从而得到预测效果更准确的LSTM模型。

1 基于多项式修正的LSTM模型设计

1.1 基于多项式修正的LSTM模型总体设计

基于强化学习（将多个模型的输出结果通过某一规则融合修正从而得到更符合需求的模型）的思想，本文设计出基于多项式修正的LSTM模型。利用多个LSTM模型对同一数据样本的不同特征进行特征提取与迭代训练。最后利用多项式拟合的方法对不同LSTM模型的输出进行多项式加权修正，以此来取得更好的预测结果。此外，不同的LSTM模型可以并行训练，减少模型整体的训练时间，极大提高模型的训练效率。总体模型结构设计见图1。

其中数据集来自CICIDS中的网络流量数据。初期通过数据分析、数理统计等手段划分出内生性特征和外生性特征数据集，分别将其输入到不同结构的LSTM模型中。LSTM模型的搭建采用了Tensorflow2框架中的序列组网，可以高效地进行模型的训练。而最后多项式修正的目的是寻求一组合适的系数｛a1,a2,…,an｝，尽量保证拟合方程得到的数据尽可能地与实际样本数据相重合。通过多项式拟合来相互修正两个LSTM模型结果的偏差，从而达到更精确地预测值Y′。至此，基于多项式修正的LSTM模型可以简化为：

Y（x1,x2）=a0+a1x12+a2x22+a3x1x2+a4x1+a5x2

其中，x1为LSTM_1模型的输出（提取结果1)，x2为LSTM_2模型的输出（提取结果2)。具体步骤如下所述。

1.1.1 数据预处理

通过不同的预处理方法，构造内生性特征的样本集和外生性特征的样本集。

1.1.2 内生性特征数据

（1）选取相邻时期的流量速率分别作为自变量和因变量。

（2）进行数据归一化，防止不同量纲的影响(归一化后的x=(x-xmean)/(xmax-xmin))。

（3）通过滑动窗口[1](选取输入滑动窗口大小k=400，标签滑动窗口大小j=64）的方法构造样本集。构造历史时刻样本集和训练标签样本集。

划分结果为：对于第i个样本，其输入为：xi=ri,ri+1,ri+2,…ri+k,(k=400)。

对应的标签为：yi=ri,ri+1,ri+2,…,ri+j,(j=64)。

（4）划分训练集和验证集，比例为8∶2（划分训练集和验证集必须在构造完滑动窗口之后进行。如果提前划分将打乱数据的时序结构，将会无法达到预期的结果）。

1.1.3 外生性特征的提取

（1）选取外生性特征，见表1，包含Flow_rate,Flow_IAT_Std,Bwd_Packets/s，Init_Win_bytes_forward等共11个特征。

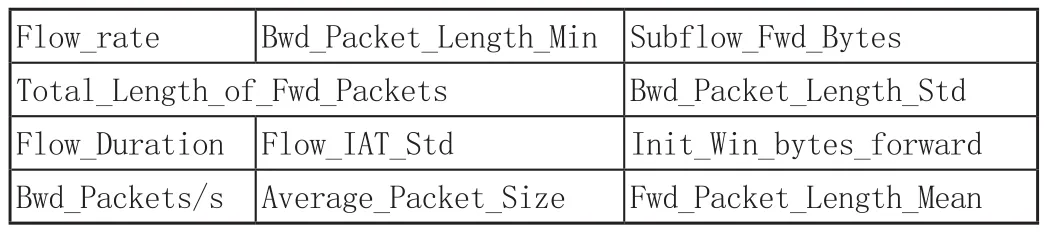
表1 外生性特征

（2）进行数据归一化处理，消除特征中不同量纲之间的影响。该步骤必须进行，否则容易造成“梯度爆炸或梯度消失”等问题。

（3）通过滑动窗口（选取输入滑动窗口大小k=400，标签滑动窗口大小n=64）的方法构造样本集。构造历史时刻样本集和训练标签样本集。

划分结果为：对于第个样本，其输入为

Xi=[r1,i,r1,i+1,r1,i+2,…,r1,i+k;r2,i,r2,i+1,r2,i+2,…,r2,i+k;…;rj,i,rj,i+1,rj,i+2,…,xj,i+k;]

其中j为特征个数。

第个样本标签为：yi=r1,r2,r3,…,rn-1,rn。

（4）划分训练集和验证集，比例为8∶2。

1.2 LSTM_1的设计

LSTM_1是通过LSTM神经网络和全连接网络的组合，使得计算后的结果尽可能地逼近真实值Y。同时，利用Loss函数作为评估标准，不断地通过迭代训练模型更新网络参数至模型收敛，从而达到预测的目的。

其中的LSTM神经网络是为解决RNN不能学习长期历史信息的问题而提出的模型，其独特“门机制”在时间序列预测方面颇见成效。该模型特殊的“记忆细胞”将自身的真实值与之前积累的外部信息相互结合，从而利用长期的信息进行学习[2]。LSTM神经网络结构见图2。

其中LSTM单元内部由各种“门”结构组成，每一个“门”结构发挥一种特定的功能，其中不同的“门”发挥着不同的作用。

遗忘门：完全保持历史信息或者完全摆脱历史信息(反映历史信息的自相关系数)。计算公式为:ft=σ(Wf·[ht-1,xt]+bf)。输入层门：决定将更新哪些值。计算公式为：。更新门：放弃了关于旧信息并添加新信息。计算公式为:Ct=ft*Ct-1+it*Ct~。输出门：决定要输出的单元状态的哪些部分。计算公式为。上述使用的激活函数均为：tanh(x)=(ex-e-x)/(ex+e-x)。

LSTM_1的内部结构及其参数见表2。表2从左至右，对应图2中的由下至上，括号内的参数为depth的值，参数共计616 440。该部分模型共有3个LSTM层，2个Dropout层和1个Dense(全连接)层。使用多层的LSTM可以更充分地提取数据的历史信息。Dropout层可以随机选取样本进行训练，预防过拟合现象的出现，使得模型在验证集中也能够取得较好的效果。

表2 LSTM各层模型选择1

以内生性数据特征作为该模型的输入，构建batch依次送入LSTM_1模型进行训练模型的参数，并将真实的结果值作为标签。

该部分模型的Loss函数选取平均绝对误差MAE(X,h)=1/mh(xi)-yi|，其中m为样本个数，h为回归函数，yi为真实值。优化器(optimizer)选取RMSprop(均方根反向传播)。其训练步骤为：（1）从训练集中取m个样本为｛x1,...,xm｝,对应的目标为yi。（2）将数据样本输入至LSTM自回归模型计算结果及损失。（3）计算各层梯度:g=1/m▽θ∑iL(f(xi;θ),yi)。（4）累积平方梯度：E[g2]t=ρ*E[g2]t-1+(1-ρ)*gt2。（5）计算参数更新。（6）重复上述步骤直至收敛，得到最终的模型及其参数值。

1.3 LSTM_2的设计

LSTM_2的内部网络结构与LSTM_1相似，但在层结构的搭建上有所不同。

LSTM_2模型的层结构及其参数，见表3，从左至右，对应图2中由下至上，表3中的3个Dense层作为整体的全连接网络层，参数共计1 428 572。LSTM_2模型依旧采用了3层的LSTM层，但为了增加该模型的性能，使用了3个DNN全连接层，且额外添加了l1，l2约束，使得模型具有更高的鲁棒性和健壮性。

表3 LSTM各层模型选择2

以外生性数据特征作为该模型的输入，构建batch依次送入LSTM_2模型进行训练模型的参数，并将真实的结果值作为标签。

该部分模型的Loss函数选取均方误差Mse(X,h)=1/m(h(xi)-yi)2,其中m为样本数，h为回归函数。优化器(optimizer)选取Adam(Momentum+RMSProp)。其训练步骤为：（1）从外生性特征样本中取出m个样本｛X1,X2,...,Xm｝（其中Xi=｛xi1,xi2,...,xij|j:特征数｝）),对应标签为yi。（2）将样本数据和标签输入多特征LSTM模型计算结果及损失。（3）计算各层梯度。（4）更新矩估计：。（5）修正偏差：。（6）更新初始值：。（7）重复上述步骤直至收敛，得到最终的模型及其参数值。

经过了50轮的训练后，LSTM_1(左)和LSTM_2(右)模型的训练结果(loss值)见图3。

2 预测结果及分析

为了比较本文提出的模型的准确度以及性能，选择了传统的GRACH模型、LSTM自回归模型以及基于多特征的LSTM模型进行对比。上述各个预测效果见表4。

表4 预测模型效果对比

图4(a)、图4(b)、图4(c)分别为GRACH模型[3-4]、LSTM自回归模型以及基于多特征的LSTM模型的预测效果。其中GRACH模型的预测仅能反映出某种趋势，而且失真比较严重。此类预测模型的优点是所需特征简单，且不需要大量数据来支撑训练，可依靠自身历史信息的相关性来进行预测。但此方法受到一定程度的限制，需要数据具有自相关性且必须通过相应的数据检验才能保证其准确性，否则会造成严重的失真现象。

LSTM自回归的预测结果如图4(b)所示。与GARCH模型相比较，LSTM神经网络的优势及其能够学习长期历史信息的特性，使得其在拟合优度方面已经有了极大地改善，尤其是对于一些处于极点的值有了准确的预测效果。如图4(c)所示，再增加多特征后的LSTM自回归模型[5-6]在原有基础上预测准确度有所提升，同时也说明了外生变量在一定程度上对于数据的预测有优化作用。这证明了本文提出区分外生性特征和内生性特征的必要性。基于多项式修正的LSTM模型的预测结果见图5。

虽然本文提出的模型相比于基于多特征的LSTM模型的准确程度并未有明显增加。但是后者在训练过程中极易因“输入过于复杂或产生稀疏矩阵”等情况而出现“梯度消失”等问题，从而造成训练效果不佳，甚至出现负数的情况。而本文设计的多项式修正的LSTM模型由于采用的是“强化学习”的思想，恰好可以有效减少此类问题的出现。多项式修正的详细结果见表5。

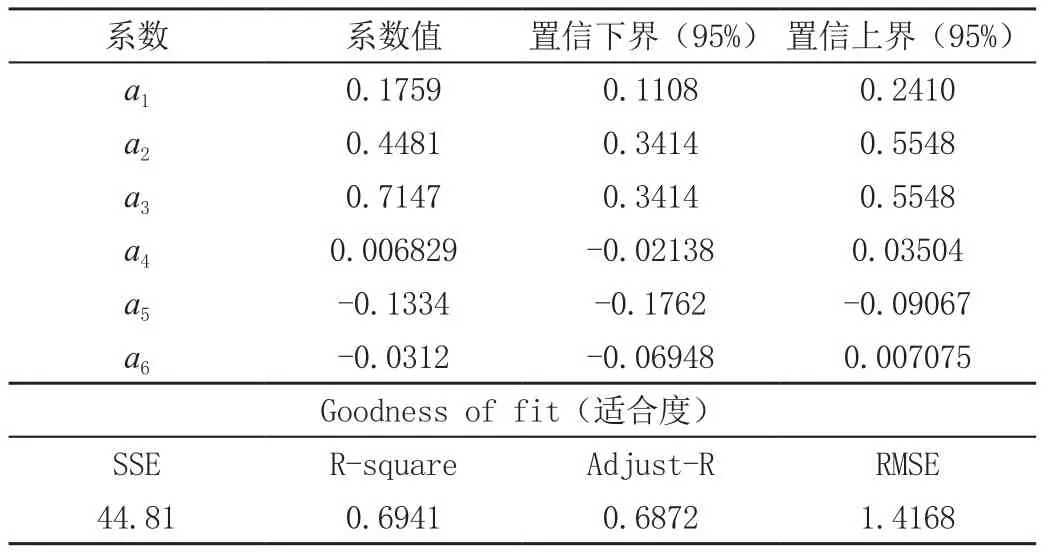
表5 多项式修正系数解析

由此表得出最终的多项式修正LSTM模型的计算公式为：y(x1,x2)=0.18+0.45x12+0.71x22+0.06x1x2-0.13x1-0.03x2。

3 结语

综上所述，对于不同的模型有着不同的应用场合。当所拥有的数据样本有限时，此时无法建立LSTM模型，只能采用对数据样本数量要求不高的GARCH模型。当拥有较多的数据样本支撑时，可以采用LSTM自回归模型和多特征LSTM模型进行预测。这两者的区别在于前者对于输入特征的要求简单，易于获取，但预测的准确度不及后者。而后者虽然预测准确度较高，有较大的抗干扰能力，但其需要多个特征的输入，而较多特征会使网络的复杂度呈指数级增长，将耗费大量时间进行训练，甚至训练无法收敛。因此，本文提出的方法可以使得多个LSTM模型同时训练，极大地降低了模型训练以及达到收敛所需的时间。并且最后将各模型的输出结果通过多项式拟合修正，得到一个性能更好，准确度较高的融合模型。

此外，当数据集划分不同输入特征后，仅有一个内生性特征时，本文提出的模型将会“退化”LSTM自回归模型，可以适用于对多维输入数据获取不易的场合。