武汉近41年浅层地温演变特征及气候影响因素分析
2022-09-07杨培强樊帆曹恒煜
杨培强,樊帆,曹恒煜
(1.武汉市蔡甸区气象局,湖北 武汉 430100;2.长江大学经济与管理学院,湖北 荆州 434000;3.武汉市气象局,湖北 武汉 430040)
0 引言
近年来,气候变化逐渐成为国际社会的重要关切[1],全球气候变暖已成为不争的事实[2].2018年IPCC发布的《全球升温1.5 ℃特别报告》指出,全球每十年升温(0.2±0.1)℃,预计全球气温在2030—2052年会比工业化之前的水平升高1.5 ℃[3].与此同时,近130多年(1880—2012年)来,全球地表平均温度上升约0.85 ℃[4].中国气象局气候变化中心发布的《中国气候变化蓝皮书(2020)》显示,中国是全球气候变化的敏感区和影响显著区,1901—2019年,中国地表年平均气温呈显著上升趋势,近20年是20世纪初以来的最暖时期[5].浅层地温是最重要的农业生产、生态环境条件之一,地温变化将深刻影响农业生产和生态环境[6-8],可见研究地温的气候变化特征具有重要的意义.近些年,地温变暖的现象越来越受到关注,各地学者已开展诸多关于不同地区、不同深度地温变化规律及成因的相关研究[9-18].但是,由于各地气候、地理和土壤性质的差异性,区域性的地温变化特征及其与控制因素的响应关系仍缺乏较全面的研究.
武汉市作为国家中心城市,随着城市化进程的不断推进,城镇化与生态环境协调发展的问题也日益突出[19].本研究运用气候学分析统计方法,对武汉1980—2020年浅层地温的变化趋势及其对大气中相关影响因素的响应关系进行分析研究,旨在为应对区域气候变化、合理利用气候资源和生态文明建设提供科学依据.
1 资料来源
本研究采用武汉国家基本气象站(以下简称武汉站)1980—2020年浅层地温资料作为研究主体,主要是考虑浅层地温距离地表近,受气候扰动的影响较大[20],更易揭示其与气候变化的关系,根据浅层地温为“距离地面0 cm至40 cm(不含0 cm和40 cm)深度处的土壤温度”的定义[21],最终选用5、10、15、20 cm地温观测项目作为研究对象.按照我国气象划分法,设定春季为每年3—5月份、夏季为6—8月份、秋季为9—11月份、冬季为12月份—次年2月份[22],以此统计整理出月、季和年序列,用以分析武汉1980—2020年浅层地温的变化特征及其对大气中相关影响因素的响应关系.
引起气象要素观测数据变化的因素,既有气候变化的自然因素,也有台站迁站等人为因素,目前国内部分地区的气象站在迁站后出现了气象要素序列非均一性的问题[23-27].2010年武汉站迁移站址(表1),其地温序列在迁站后(2010年)存在明显降低现象(图1).为分析浅层地温显著降低是自然因素还是人为因素引起,选取蔡甸国家一般气象站(以下简称蔡甸站)浅层地温资料做对比分析,蔡甸站观测资料均一性较好且距武汉站较近,经检验蔡甸站浅层地温序列在2010年后变化较平缓且未发生显著降温现象,同时武汉站在2009年开展了为期一年的对比观测试验(新站与旧站同时运行),经实际观测,新站5~20 cm地温年平均值较旧站分别降低0.7、0.6、0.3、0.3 ℃.综合来看,台站迁站是武汉站浅层地温序列在2010年显著降低的主要因素,气温序列也有类似现象及成因,具体分析不再赘述.
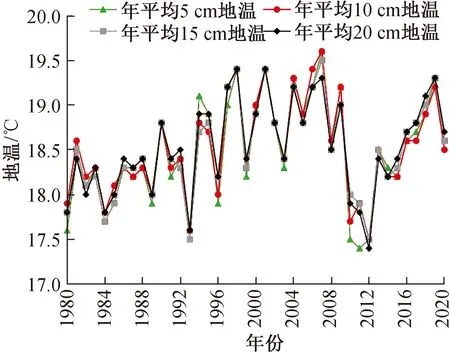
图1 1980—2020年武汉浅层地温年平均变化

表1 武汉国家基本气象站站址变动情况表
2 研究方法
2.1 非参数Mann-Kendall趋势检验在Mann-Kendall检验中,设时间序列数据xi(1,2,…,n)是n个独立的、随机变量同分布的样本.定义某样本序列变化趋势统计量S为:
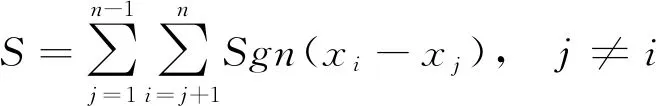
(1)
其中Sgn(xi-xj)为符号函数,当自变量为正数、零、负值时分别为1、0、-1,因此定义Sgn(xi-xj)为:
(2)
S为正态分布,其均值为0,方差Var(S)=n(n-1)(2n+5)/18.当选择的样本为长序列(n>30)时,标准化的正态分布变化趋势统计量Z的计算式为:
(3)
在双边趋势检验中,对于给定的显著性水平α,若︱Z︱≤Z1-a/2,则接受原假设H0(无变化趋势),若|Z|>Z1-a/2,则原假设H0是不可接受的,时间序列数据存在明显的升高或降低趋势.Z为正值表示升高趋势,负值则表示降低趋势.且︱Z︱≥1.28、1.64、2.32时,表示分别通过了置信度90%、95%、99%显著性检验.
2.2 Mann-kendall检验法突变分析在Mann-Kendall检验中,设时间序列数据xi(1,2,…,n)是n个独立的、随机变量同分布的样本.定义某时间样本序列变化趋势统计量Sk为:
(4)

(5)
给定显著性水平α=0.05,查正态分布表,若|UFk|>1.96,则表明序列存在明显的趋势变化,UFk正值表示升高趋势,负值则表示降低趋势,将统计序列UFk的所有数值在折线图中连一条曲线(UF),通过信度检验(±1.96)可得出其是否有明显的变化趋势.之后,把此方法应用到反序列中,计算得到另一条曲线(UB),两条曲线在置信区间内的交点则确定为突变点.
2.3 相关系数利用斯皮尔曼相关系数进行序列相关性分析,公式如下:
(6)
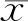
2.4 气候倾向率采用一元线性方程进行气候倾向率研究,即:
y=a0+a1t
(7)
其中,y为平均地温,a0为常数,a1为线性趋势项,t为时间,a1×10为拟合出的一元线性方程斜率的10倍,表示武汉多年平均浅层地温每10 a的演变趋势.如果拟合出的方程斜率大于0,即a1>0时,表示浅层地温总体上呈升高的变化趋势;反之表示序列总体上呈降低的变化趋势.
3 武汉近41年浅层地温演变特征
3.1 浅层地温年际变化特征武汉浅层地温(5~20 cm)近41年平均值分别为18.49、18.53、18.52、18.53 ℃;浅层地温近41年年序列中,年均值最高为19.6 ℃,出现在2007年(5 cm、10 cm地温),最低值为17.4 ℃,出现在2011年(5 cm),各层地温年均最高与最低值差值非常接近(2.0~2.2 ℃).总体来看(图1),武汉浅层地温的年平均值整体呈波动状缓慢升高趋势, 且各土层地温变化趋势较为一致.
3.2 Mann-Kendall检验法进行年际变化趋势分析将武汉近41年浅层地温年平均序列采用Mann-Kendall检验法进行序列趋势检验,首先确定样本序列变化趋势统计量S,再通过标准化处理,得出标准化的正态分布变化趋势统计量Z,如表2所示,不同深度浅层地温的Mann-Kendall变化趋势检验统计结果为正且大于1.64,表明浅层地温序列整体存在显著升高的变化趋势,并且均通过了置信度95%的显著性检验,同时各层浅层地温趋势检验统计量Z值较为接近(1.87~2.37),表明5~20 cm地温的变化趋势具有较好的一致性.

表2 1980—2020年武汉浅层地温变化趋势检验统计结果
3.3 Mann-Kendall检验法进行年际变化突变检验为进一步研究各序列演变情况,采用Mann-Kendall检验法进行序列突变检验.近41年武汉浅层地温突变检验结果详见图2,其中图2(a)、(b)、(c)、(d)分别演示了5~20 cm地温年序列的演变特征和突变情况.由4图中UF、UB曲线变化可以发现,不同深度地温在1980—2020年的演变过程大体较相似,但也存在局部的差异性.从序列变化趋势来看,各层浅层地温序列在1984—1986年期间检验出的UF曲线低于X轴(UF<0),同时10 cm地温在1986—1990年的UF值也小于0,其他年份的5~20 cm地温UF曲线均高于X轴(UF>0),且在2000—2009年期间均超过了阈值线(U0.05=1.96),检验结果表明,各层浅层地温在1980—2020年期间虽然存在持续时间较短的降低过程,但总体处于不断升高的趋势,且在2000—2009年期间存在显著升高的变化过程,并通过了置信度95%的显著性检验;从序列突变情况来看,4个分图中检验出的UF和UB两条曲线均在2001—2002年期间有多个交点,根据Mann-Kendall突变检验算法定义及上文关于迁站对武汉站浅层地温序列影响的分析结果得出,武汉5~20 cm地温在1990年、2017年前后存在气候突变,5 cm和20 cm地温在2009年发生的突变是台站迁站等人为因素引起的.

图2 1980—2020年武汉浅层地温突变检验曲线图
4 武汉近41年浅层地温变化的气候影响因素分析
4.1 相关性研究地表与大气的联系最为紧密[28],采用斯皮尔曼相关系数的分析方法,研究武汉近41年年均浅层地温与年均气温、风速、气压、日照以及年降水量这5个气候因子之间的相关性.浅层地温与不同气侯因子相关性研究统计结果(表3)表明,浅层地温与气温等气候因子均存在不同程度的相关关系.
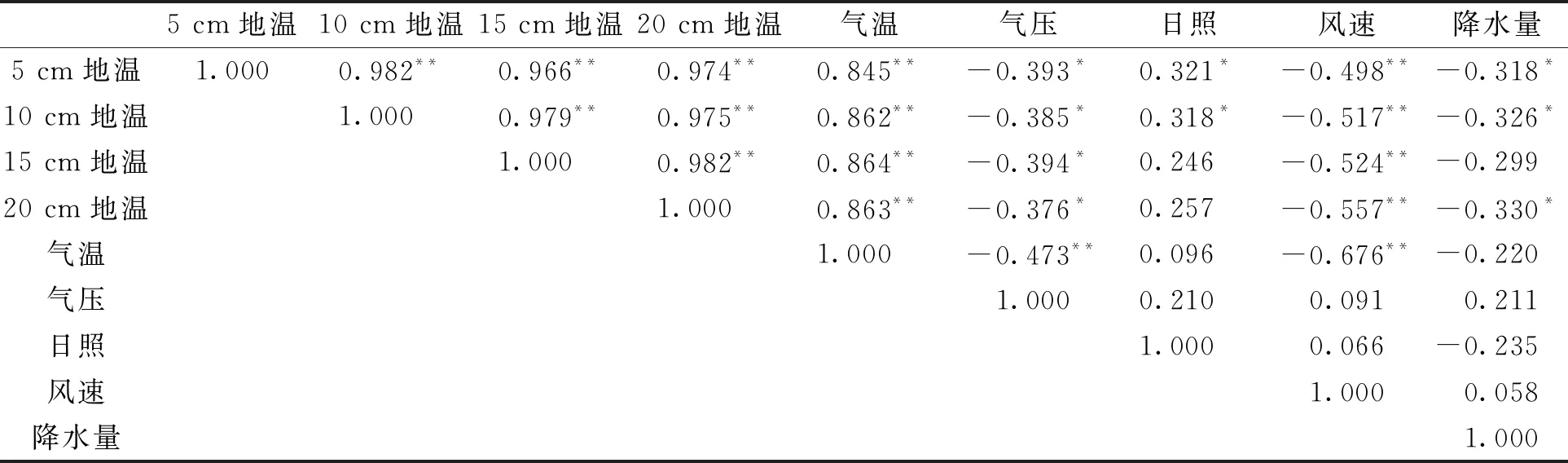
表3 1980—2020年武汉浅层地温与不同气候因子相关性研究统计结果
从浅层地温与气温相关性来看,其相关系数均大于0.845,且通过了0.01的显著性检验,表明气温与浅层地温之间存在较强的正相关关系.浅层地温与风速、降水量、气压、日照等气候因子也存在弱相关关系,其中与风速的相关程度相对较高,且通过了0.01的显著性检验.综合来看,气温的升高是浅层地温显著增温的最主要因素,风速、降水量、气压、日照作用次之.从不同深度的浅层地温之间的相关性来看,其相关系数均超过了0.966,且通过了0.01的显著性检验,说明各层地温之间存在极强的正相关关系.
4.2 浅层地温及气温月变化剖面图分析在相关性研究中发现浅层地温与气温序列存在较强的正相关关系,但与其他气候因子相关程度较弱.通过作垂直剖面图(图3)进一步研究浅层地温及气温月变化关系,图中纵坐标自下而上依次为气温、5 cm地温、10 cm地温、15 cm地温、20 cm地温5个观测项目,横坐标表示月份.从地气温差变化来看,各月浅层地温与气温的差值均为正值,表明同月气温较地温明显偏低,地表对大气的加热作用大于冷却作用,以向大气输送热量居主导地位[29].在四季中夏季地气温差最小,表明夏季太阳辐射较强,气温升幅较快,地表对大气的加热作用相对变小;从逐月变化情况来看,各月平均地温与气温的最低值均出现在1月,其后逐步升高,7—8月达到峰值,随后逐渐降低,月变化较为同步.

图3 1980—2020年武汉气温和浅层地温月平均剖面图
4.3 浅层地温与气温变化趋势的关系利用1980—2020年的年均气温和年均5 cm地温资料,建立一元线性回归方程(图4),所建函数在该区间内具有明显的单调性(单调增加),进一步反映了5 cm地温与气温的变化趋势存在较强的同步性,其他深度的浅层地温与气温变化的关系大体相同,不再重复赘述.
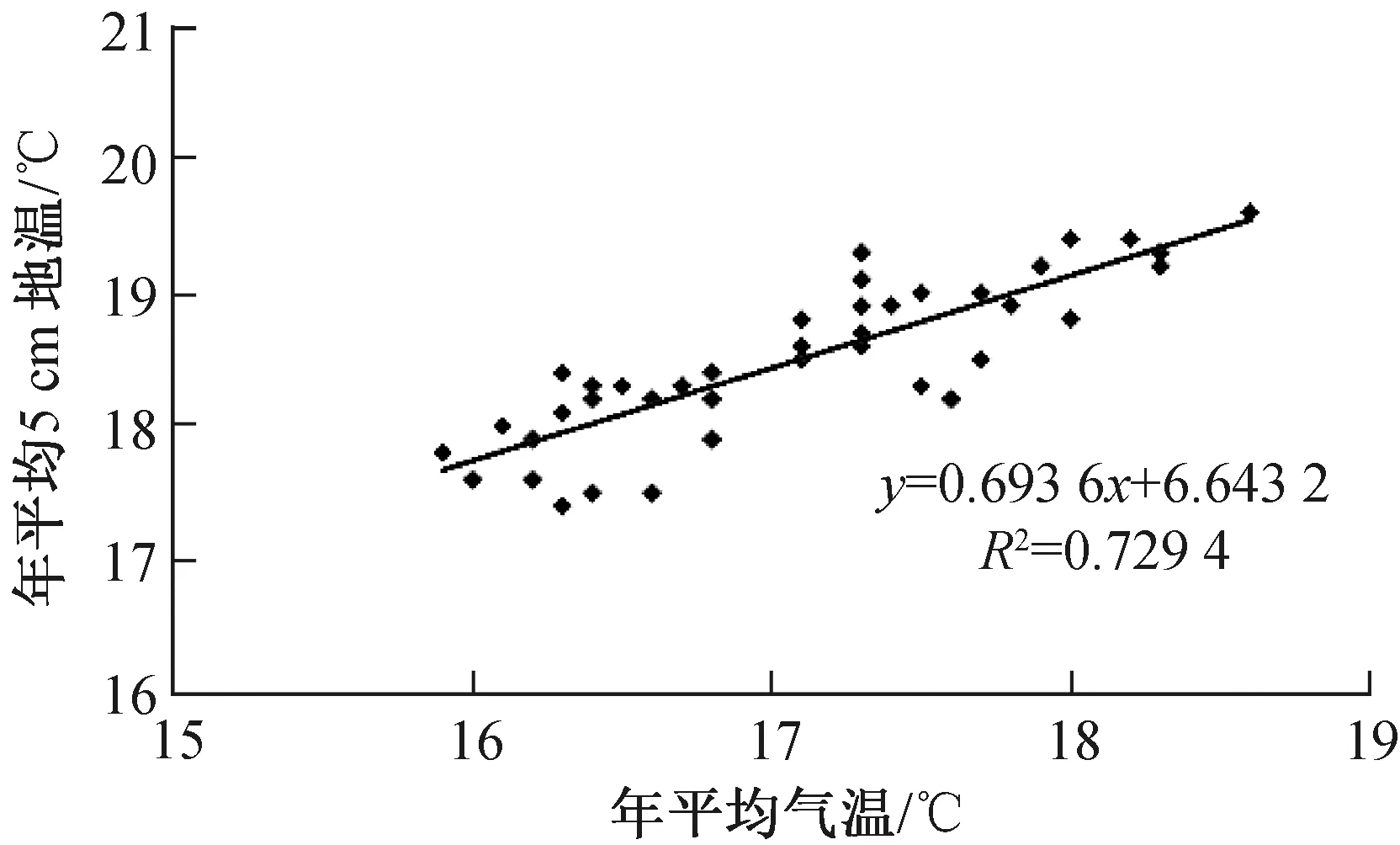
图4 1980—2020年武汉5 cm年均地温和年均气温线性回归关系
4.4 浅层地温与气温的气候倾向率变化关系武汉近41年浅层地温和气温的四季气候倾向率变化情况如表4所示.从全年气候倾向率变化来看,浅层地温对气候变暖的响应也较强[30],武汉浅层地温和气温均呈明显的升高趋势,但浅层地温升温率低于气温,其中浅层地温升幅为0.117~0.151 ℃/10 a,气温升幅为0.279 ℃/10 a;从四季气候倾向率变化来看,浅层地温与气温均为春季升温率最大,春季升温率最大表明了浅层地温的显著升高主要得益于春季气温的升高[31],但是浅层地温在夏季升温率最低,气温则在冬季升温率最低,说明浅层地温与气温不同季节气候倾向率变化也存在一定的非对称性.

表4 1980—2020年武汉浅层地温与气温四季气候倾向率变化 ℃·(10a)-1
近41年武汉浅层地温与气温在各年代气候倾向率变化如表5所示.从整体情况来看,浅层地温与气温存在一个逐渐加速变暖的过程,其中,1980s期间浅层地温与气温缓慢升高,1990s期间升温率逐渐加快,但在2000s期间气候倾向率均为负值,台站迁站是影响气候倾向率为负值的主要因素,并非气候变化因素引起,2010s期间又出现更加显著的升温过程;从各年代升温变化来看,浅层地温与气温均在1980s升幅最小,气温在1990s升幅最大,浅层地温则在2010s期间升温更为显著,且其升温幅度超过了气温.

表5 1980—2020年武汉浅层地温与气温不同年代气候倾向率变化
4.5 浅层地温与各气候因子关系的多元线性回归预测模型和效果检验在相关性研究中发现,影响浅层地温的气候因子有多个,然而各因子之间相互影响、关联复杂,例如气温和日照之间可能存在共线性的问题,这时因子之间相关程度的强弱并不能完全代表实际情况.故需通过多元线性回归方法,得出浅层地温对气候因子变化的响应关系,最终建立浅层地温与各气候因子关系的预测模型.不同季节武汉浅层地温与各气候因子的多元线性回归响应关系详见表6,其中回归方程中的x1、x2、x3、x4、x5和y分别代表气温、风速、日照数、降水量、气压与浅层地温,各回归方程共线性问题良好,拟合情况较好.

表6 不同季节武汉浅层地温与各气候因子的多元线性回归响应关系
利用浅层地温多元线性回归预测模型和2021年1—9月观测资料,得出同时段内的不同深度浅层地温预测值,不同深度月平均地温预测值与实测值的绝对误差详见表7,其数值均在1 ℃以下(包含1 ℃),0.5 ℃以下(包含0.5)的误差数值占比66.7%,其中最大和最小绝对误差分别为1 ℃、0 ℃.通过实际检验的预测值与实测值误差总体较小,预测模型拟合较好,精度较高.

表7 不同深度月平均地温预测值与实测值的绝对误差 ℃
5 结论
本文中主要利用武汉1980—2020年地面气象实际观测资料(浅层地温和气温、气压、降水量、日照、风速),采用了Mann-Kendall检验法、相关性研究、气候倾向率、线性回归等研究方法,对武汉1980—2020年浅层地温的演变规律及其与气温、风速、气压、降水量以及日照数等气候因子变化的相关关系进行分析,并建立多元线性回归预测模型.主要有以下结论:
1)武汉浅层地温在1980—2020年期间虽然存在持续时间较短的降低过程,但总体处于不断升高的趋势,且在2000—2009年期间存在着显著升高的变化过程,这种显著升高的趋势检验通过了置信度95%的显著性检验.
2)在Mann-Kendall趋势检验中,浅层地温趋势检验统计量Z值较为接近(1.87~2.37),表明武汉各层浅层地温的变化趋势具有较好的一致性,在Mann-Kendall突变检验中,武汉5~20 cm地温在1990年、2017年前后存在气候突变,5 cm和20 cm地温在2009年发生的突变是台站迁站等人为因素引起的.
3)气温的升高是浅层地温显著增温的主要因素,风速、气压、日照、降水量作用次之,其中浅层地温与气温之间有较强的正相关关系(相关系数0.845~0.864).同时各层浅层地温序列之间存在极强正相关关系(相关系数0.966~0.982).
4)近41年浅层地温与气温不仅存在较明显的同步性,还存在一定的非对称性.其中,浅层地温和气温都呈明显的升高趋势,浅层地温升温率总体低于气温升温率,但浅层地温在2010s期间升温更为显著,且其升温幅度超过了气温;浅层地温的显著升高主要得益于春季气温的升高,浅层地温与气温均为春季升温率最大,但浅层地温在夏季升温率最低,而气温则在冬季升温率最低;浅层地温与气温同时存在一个逐渐加速变暖的过程;浅层地温与气温最低值均出现在1月,7—8月达到峰值.
5)浅层地温与各气候因子关系的多元线性回归预测模型经实际检验的绝对误差均在1 ℃以内,0.5 ℃以下的误差数值占比66.7%,其中最大和最小绝对误差分别为1 ℃、0 ℃.模型误差小、精度高,较好地拟合浅层地温对气候因子变化的响应关系.
致谢论文撰写过程中湖北省气象服务中心陈正洪教授对笔者进行了指导、提出了宝贵的修改建议,在此表示衷心感谢.
