锅炉飞灰BP-WA算法优化控制策略

章家岩，陈雨薇，宋澜波，冯旭刚

(1.安徽工业大学电气与信息工程学院，安徽 马鞍山 243032；2.湖南华菱涟源钢铁有限公司能源总厂， 湖南 娄底 417009)

飞灰含碳量是影响锅炉热效率的重要指标之一，影响燃煤锅炉飞灰含碳量的因素多且杂，包括煤种、锅炉设计结构、运行参数等，所以采用简单的公式无法对其进行估算[1].针对此情况，国内外众多学者采用了多种先进测量方法对飞灰含碳量的在线测量问题进行深入研究，主要以软测量和信息融合方法为主.其中，李霞等[2]将迭代混沌映射替代高斯分布，结合涡流搜索算法设计了一种基于量子迭代混沌的涡流搜索算法预测模型，解决了模型迭代过程中陷入局部最优与解单一问题，但该研究并未考虑飞灰含碳量输入参数过多问题，导致全局搜索时间较慢，预测结果的实时性与准确性不高.洪昌少等[3]采用一种基于BP/RBF神经网络耦合模糊规则，对电站机组燃烧控制进行建模，解决了发电效率和NOx排放的综合问题，但其针对锅炉燃烧优化应用问题尚未做出更深一步的研究.神经网络已被广泛应用于工业现场控制问题，且取得了良好的应用效果，但较为先进的网络如RBF神经网络、卷积神经网络等结构较为复杂，难以适用于复杂的工业现场环境.为此，本研究将BP神经网络引入测量环节，在其基础上针对目前飞灰含碳量在线测量存在样本误差以及输入参数过多等问题，采用信息熵改进标准BP神经网络的误差函数，此外，采用主元分析剔除飞灰预测模型冗余参数，提高模型应用性.同时，建立以最低飞灰含碳量为目标函数的狼群寻优模型，实时调整发电机组运行中各工况参数，提高其运行效率.最后将改进后的优化算法通过Matlab验证其有效性，可为电厂锅炉实际运行工况调整的实时性、准确性和高效性做出重要指导作用.

1 基于信息熵的改进型BP神经网络算法

1.1 BP神经网络的基本原理BP神经网络是一种多层前馈型神经网络，可表达难以建模的非线性系统，信号在该网络中前向传递，误差反向传播，通过训练使网络具备预测非线性系统输出的能力[4].图1给出一个三层BP网络结构，每一层的权值都可以通过学习来调整[5].因其具有较强的非线性处理能力，已被逐步应用于飞灰含碳量的在线监测研究中.BP神经网络在应用过程中初始权值和阈值随机选取，容易出现局部收敛极小点，从而降低拟合效果，导致预测与期望的误差仍然比较大.所以针对这一问题，对BP神经网络进行改进[6-7].

图1 BP神经网络结构

1.2 BP神经网络误差函数改进

1.2.1 基于信息熵的误差函数改进 假设神经网络所训练飞灰工况参数样本集合为R={(ri,zi),i=1,2,…,m}，系统的输出干扰为n1～N1(0,σ)时，则此时系统的输出可设为zi=g(ri)+ni，其中g(ri)为飞灰样本真实参数，ni为随机干扰噪声，无法准确判断其模型信息，并对系统实际输出进行干扰补偿.但如果在f(r,w)上加上已知分布的干扰n～N(0,β2),之后调整神经网络的权值与阈值以及β2使得z=f(r,w)+n与zi=g(ri)+ni相互逼近，此时，只要z=zi，得到的f(r,w)即为系统的实际输出g(ri).

将该集合R中每个工况参数的信息量I(ri)的数学期望记为信息熵H(R).则有：

(1)

对于时间ri来说，若将该时间下的工况参数发生的概率记为pi，则:

(2)

为避免采用BP网络训练模型时，受样本数据误差影响而产生“过拟合”问题，须对其网络结构做出改进.

1.2.2 神经网络的学习误差函数改进设计 在BP模型中加入干扰N，得到预测结果f(r,w)的方差为β2，此时将(r,z)在输入输出空间R·Z中发生概率记为pw，σ(r,z)，将r在整体输入空间中概率密度记为p(r).

(3)

设定样本噪声为n1，此时定义真实系统为z=g(r)+n1，其概率记为Pw,σ(r,z)，方差为σ1.此时定义pw，σ(r,z)与z=g(r)+n1之间的信息熵为I：

I=I(Pw1,σ1(r,z)，Pw,σ(r,z))

=J(w,σ)+Hw1

(4)

其中

(5)

其中

(6)

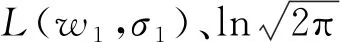
(7)

且Hw1=J(w1,σ1)与权值w和方差σ无关.

有且仅有两种网络权值与方差都相等的情况下，二者之间的概率描述为0，也即二者信息距离等于0,此时可用f(r,w)来精准表述真实系统g(r).所以将0作为信息距离的设定值，并以此信息距离函数作为BP模型的学习误差函数模型，并对BP模型结构进行优化改进，可达到降噪效果.因此，将上述已改进的BP网络模型设定最优化目标：信息距离0进行训练，过程如下.

min{I(Pw1,σ1(r,z),Pw,σ(r,z)),σ≥0}

(8)

又Hw1=J(w1,σ1)与w,σ无关，简化得

min{J(w,σ),σ≥0}

(9)

即令J(w,σ)作为神经网络误差函数.再将简化后的神经网络误差函数J(w,σ)结合神经网络预测泛化误差Eg大小，过程如下：

(10)

其中z(r)为实际输出值，f(r,z,w,σ)为神经网络模型.则J(w,σ)可表示为：

(11)

由于w,σ暂且未知，所以在误差函数优化设计过程中，将该优化过程转变为最小二乘问题进行处理可减少算法优化步骤.

σ2=Eg(w)

(12)

因此，对神经网络误差函数优化等价于：

(13)

由式(13)可知，J和Eg的关系为线性正相关.由于式(13)中Eg与扰动信号具体参数不明，所以需要先由输入样本数据集D来构造Eg与方差的相关函数.

由式(12)得出Eg与样本方差均值相关，所以Eg(w)可做如下变换：

(14)

考虑到用f(r,w)+n去逼近样本集D，因此误差ni可表示为：

ni=zi-f(w,ri),(ri,zi)∈D

(15)

且ni的分布满足N(0,σ2)，因此采用下式对此σ2进行逼近：

(16)

将式(16)代入式(13)，则误差函数为：

(17)

从上述过程可知，误差函数J(w,σ)经过优化改进，已经较未改进之前简化了所需优化参数的数量.用此时的误差函数式(17)来进行BP算法的权值优化，可较大程度地降低噪声对优化过程的影响.

2 飞灰含碳量预测模型建立与实现

飞灰含碳量是与锅炉效率密切相关的重要参数，因此只有对飞灰含碳量准确测量才能保证锅炉的效率[8].对飞灰含碳量造成直接或间接影响的工况种类较多，若将所有工况参数都作为网络输入，则会增加网络输入层节点与整体复杂程度，从而降低模型效率.但如果只针对主要影响工况的参数进行选取，会造成预测模型失真等问题.因此，本研究采用主元分析法，对输入参数进行筛选，减少不必要的影响参数种类，保留影响因素较高的参数，保证预测模型的可靠性，筛选过程如下.

2.1 主元分析法介绍对于n组飞灰样本，假设各组样本中含有P个值：R1,R2,…,RP.整体样本参数可用矩阵R表示：

(18)

将飞灰参数的影响值样本中各工况参数Ri以及它们各自的权重系数aii进行线性组合来表示各工况参数对于飞灰参数的影响值：

(19)

简化F得：

Fi=ai1R1+ai1R2+…+ai1Rp(i=1,2,…,p)

(20)

式中，Ri,Fi为n维向量，a1i2+a2i2+…+api2=1(i=1,2…，p).

2.2 主元计算分析对于n维飞灰参数样本R=(R1,R2,…,Rn)T其协方差矩阵为：

(21)

得到样本的协方差矩阵Cr后，计算其特征值λi和与对应特征向量ui，并以各参数样本所得出的特征值大小顺序计算出各工况参数对飞灰含碳量的主元贡献值.

(22)

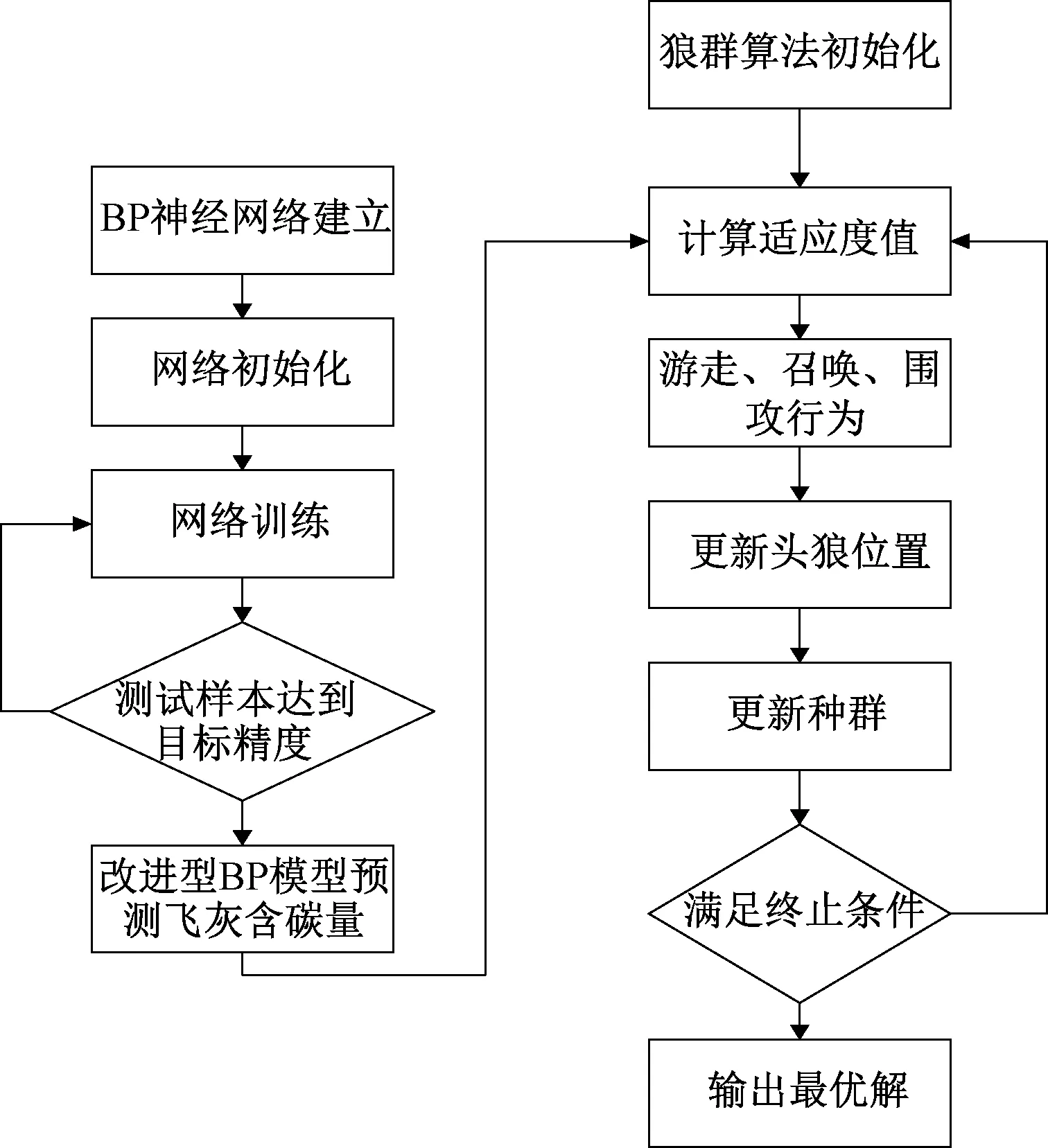
选择前m个较大特征值的特征向量作为变换矩阵TT=(u1,u2,…，um)(m

2.3 输入变量选择飞灰含碳量的高低主要受煤质及锅炉运行参数的影响，根据相关文献，以基碳、基氢、基氧、基硫、基灰分、基水分、挥发分、灰分、水分、低位发热量、煤粉浓度、锅炉负荷、一次风速、二次风门开度、配风方式、燃烧器摆角以及烟气含氧量等20余种各工况参数作为改进型BP神经网络预测模型的输入参数，飞灰含碳量作为预测模型的输出[9].以飞灰含碳量作为目标变量，通过OPC通讯方式从工厂DCS系统中采集数据，时间间隔为1 min/组，共200组.选取其中160组数据作为改进后网络模型训练样本参数，剩余40组作为验证.选取样训练样本参数前，须对数据参数进行数据归一化处理，使样本数据参数都处于[-1，1]区间内，以消除数据差异化对训练结果的影响.数据处理过程如式(23)所示.

(23)

其中，rmax、rmin分别为上述工况种类中某一种工况的最大值与最小值，rk为第k个变量的值.

3 改进型BP-WA算法优化控制研究

3.1 基于改进型BP模型飞灰预测研究将改进型BP网络模型在matlab环境中运行，依次确定网络传输函数tansig、学习函数trainlm、权值调整函数learngdm以及性能函数mse.网络输入层根据主元影响因素设置为20，输出层为1，隐含层根据公式及经验设置为10.精度误差值设置为0.001，最大迭代次数设置为1 000.

网络仿真模型采用Z=sim(net,P)，其中P为飞灰模型样本参数，Z为预测模型输出.将200组样本训练参数输入进行仿真训练，分别以改进BP网络模型预测效果与标准BP网络模型进行预测，图2所示为两种算法预测效果对比.

图2 改进型BP神经网络与标准BP神经网络预测结果对比

由图2可知，与标准BP网络模型相比，改进型BP网络模型预测结果更接近样本参数真实值，预测精度更高.为更精确地分析两种模型预测精度差异，将两种模型预测误差及误差值百分比进行相关仿真运算，图3、图4分别为改进BP模型前后误差值及误差百分比对比.

图3 改进型BP神经网络与标准BP神经网络预测误差值对比

图4 改进型BP神经网络与标准BP神经网络预测误差百分比对比

分析图3、图4误差值对比图可知，改进型BP模型误差值范围整体集中在[-0.1,0.1]，而标准BP模型误差值波动较大，相比改进模型整体误差值更高.将误差精度进行比较，改进型BP模型平均误差为0.020 8，平均误差百分比为4.22%，而标准型平均误差为0.032 9，平均误差百分比10.35%.改进型BP神经网络平均预测误差百分比仅为3.02%，普通型BP神经网络平均预测误差百分比为4.99%.可见本文中改进算法的预测效果更好且精度更高，可进一步运用至锅炉飞灰含碳量优化过程中.

3.2 基于改进型BP-WA算法飞灰优化控制根据现场锅炉实际运行工况及电厂分布式控制系统(DCS)可知，部分工况参数较为复杂，耦合因素较多.如何简化计算参数数量，提高运算速度，将飞灰含碳量预测结果反馈到DCS系统进行优化控制是目前研究的难题[10].结合现场工艺情况并在保证优化调整参数过程中不会对机组稳定运行造成影响的范围内，可供选择的优化参数种类分别为燃烧器摆角、配风方式、煤粉浓度和一次风速.

综上所述，将燃烧器摆角、配风方式、一次风浓度和一次风速当做目标优化参数，利用狼群算法(WA)[11-12]寻优上述4个燃烧参数，结合改进型BP神经网络寻求最优飞灰含碳量.设计算法步骤如图5所示.

图5 改进型BP-WA算法的机组飞灰含碳量优化控制策略流程图

分别以上述4种工况参数作为待优化目标，根据锅炉飞灰含碳量相关工艺要求，设定以飞灰含碳量为最小值的目标函数，并结合改进型BP神经网络模型，设定目标函数MinC如式(24)所示：

MinC=f(ri,w,v)，ri∈R

(24)

其中C为改进型BP算法输出值，i为工况参数个数，ri为各工况参数值，w,v为网络模型权值参数，R为所选取的工况参数数据.

采取狼群算法对锅炉飞灰含碳量进行优化控制，以式(24)为目标函数，设置算法参数：Tmax=500，种群规模N=50，探狼个数S=10，搜索步长h=1，搜索方向α=5，优化结果分析如图6所示：

图6 适应度变化曲线

分析图6可得，在20次迭代过后，适应度值稳定于3.29，达到当前工况可调整范围内的最小飞灰含碳量值，较初始飞灰含碳量值降低3.50.将优化后的一次风速、煤粉浓度、二次风配风方式和燃烧器摆角以及飞灰含碳量各工况参数变化值如表1所示，飞灰含碳量优化后效果如图7所示.

表1 算法优化后各主要工况数据变化

图7 算法优化效果

从图6和图7中可以看出，随着迭代次数的逐渐增加至20次后，适应度值不再变化，飞灰含碳量递减趋势较为明显.分析表1可以看出，当一次风速设定在27.7 m/s、煤粉浓度设定值为0.398 kgc/kga，燃烧器摆角设定为8.4°时为最佳燃烧工况，结合飞灰含碳量与上述工况变化分析，飞灰含碳量和适应度曲线的变化趋势大致相同，证明了本研究控制算法的实际有效性.

4 结论

本研究以某冶金自备电厂350 MW燃煤锅炉为对象，对BP神经网络误差函数进行改进，以提高对于输入样本存在方差未知的正态噪声干扰的预测精度，建立了飞灰含碳量的软测量模型.受到正态分布的噪声干扰时，改进型BP神经网络模型逼近效果更好，仿真验证结果表明，改进型BP神经网络与标准神经网络算法的均方误差分别为0.020 8和0.032 9，验证了模型的有效性.此外，将改进型BP网络结合WA算法建立飞灰含碳量优化控制模型，以现场工艺中可调工况参数为调节量进行仿真实验，结果表明改进型BP-WA控制策略应用前后,飞灰含碳量值由6.79%降低至3.29%，验证了本研究所提出的优化控制策略的有效性，能够为现场运行人员提供指导，具有一定程度的工程应用价值.