格蕴涵代数的Ω-犹豫模糊子代数
2022-09-07姜曼卢金梅
姜曼,卢金梅
(1.西安交通工程学院公共课部, 陕西 西安 710300;2.郑州轻工业大学数学与信息科学学院,河南 郑州 450000)
0 引言
自从模糊集[1]的概念被提出后,模糊集已经应用到生活中的各个方面.由于需要考虑元素之间非此即彼的关系,Atanassotv K[2]提出了直觉模糊集;为了解决生活中数据的区间性,Zadeh[3]提出了区间值模糊集;因为要处理不相容事物的两极性,张文冉[4]提出了双极值模糊集;由于自然界中的大部分问题的解决方案并不是确定的,Torra V[5]提出了犹豫模糊集;在Ω集的基础上,Yong B J等[6]提出了Ω-模糊集.在模糊蕴涵代数[7]的基础上,1993年徐扬[8]提出了格蕴涵代数的概念.有关模糊蕴涵代数的子代数的研究,现阶段学者们做了大量工作:比如刘熠[9]等研究了区间值(α,β)模糊格蕴涵子代数;秦学成等[10]在格蕴涵代数研究了区间值模糊子代数;傅小波等[11]研究了格蕴涵代数(∈,∈∨q(λ,μ))-模糊子代数;特别地,傅小波等[12-13]在格蕴涵代数中研究犹豫模糊LI理想与反犹豫模糊滤子.本研究把犹豫模糊集、Ω-模糊集与格蕴涵代数相结合,研究格蕴涵代数的Ω-犹豫模糊子代数及其性质,一系列结果对研究格蕴涵代数有重要的意义.
1 预备知识
定义1.1[14]设(L,∨,∧,′,→,O,I)是有界格,O是最小元,I是最大元,′:L→L是格中偏序≤的逆序对合对应,→:L×L→L是一个映射.称(L,∨,∧,′,→,O,I)是一个格蕴涵代数,如果∀x,y,z∈L,满足下列条件:
1)x→(y→z)=y→(x→z);
2)x→x=I;
3)x→y=y′→x′;
4) 若x→y=y→x=I,则x=y;
5) (x→y)→y=(y→x)→x;
6) (x∨y)→y=(x→z)∧(y→z);
7) (x∧y)→y=(x→z)∨(y→z).
简称L是格蕴涵代数.
定义1.2[15]设X,Ω为非空给定集合,映射A:X×Ω→[0,1]称为X的Ω-模糊集.
定义1.3[5]设X是一个非空经典集合,一个X上的犹豫模糊集F的定义如下:
F:{(x,hF(x))|x∈X},
其中hF(x)是由区间[0,1]上若干个不同值构成的集合,表示X中的元素x属于集合F的若干种可能隶属度.
设F为X中的犹豫模糊集,P([0,1])为区间[0,1]的幂集,称集合
X(F,γ):={x∈X|γ⊆hF(x)}
为F的犹豫水平集,其中γ⊆P([0,1]).记X中的犹豫模糊集为HF(X).
定义1.4[5]对于F∈HF(X),犹豫模糊元hF(x)的下界和上界分别定义如下:
下界:hF-(x)=minhF(x),上界:hF+(x)=maxhF(x).
犹豫模糊集的3基本运算补、并和交分别定义如下:
1)补:对于F∈HF(X),它的补元Fc定义为:
hFc(x)=∪{1-h|h∈hF(x)},
补运算满足对合律,即(Fc)c=F.
2)并:F,G∈HF(X),F和G的并F∪G定义为:∀x∈X,
hF∪G(x)=hF(x)∪hG(x)={h∈hF(x)∪hG(x)|h≥max(hF-(x),hG-(x))}.
3)交:F和G的交F∩G定义为:
hF∩G(x)=hF(x)∩hG(x)={h∈hF(x)∪hG(x)|h≤min(hF+(x),hG+(x))}.
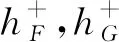
引理1.1[14]设L是格蕴涵代数,∀x,y∈L,则
1)O→x=I,x→I=I,I→x=x,x→O=x′;
2)x≤y当且仅当x→x=I;
3)x∨y=(x→y)→y.
定义1.5[14]设A⊆L,称A是L的一个格蕴涵子代数.如果A满足下列条件:
1)(A,∨,∧,′)是(L,∨,∧)的带有逆序对合、的有界子格;
2)若x,y∈A,则有x→y∈A.
引理1.2[14]设L是格蕴涵代数,A是L的一个非空子集,则A是L的一个格蕴涵子代数,如果∀x,y∈L,满足下列条件:
1)O∈A,
2) 若x,y∈A,则有x→y∈A.
定义1.6[14]设L是格蕴涵代数,A是L的一个非空子集,则A是L一个模糊格蕴涵子代数,如果∀x,y∈L,满足下列条件:
1)A(I)=A(O);
2)A(x→y)≥A(x)∧A(y).
引理1.3[8]设A是L的一个模糊格蕴涵子代数,则∀x∈L,A(I)=A(O)⊇A(x).
定义1.7[14]设L,M是格蕴涵代数,称蕴涵同态f:L→M为格蕴涵同态,如果∀x,y∈L,满足下列条件:
1)f(x→y)=f(x)→f(y);
2)f(x∨y)=f(x)∨f(y);
3)f(x∧y)=f(x)∧f(y);
4)f(x′)=(f(x))′.
设映射f:L→M为格蕴涵同态,若f是单射,则称f是单同态;若f是满射,则f是满同态;若f是双射,则称f是同构.
引理1.4[14]设L、M是格蕴涵代数,映射f:L→M为满格蕴涵同态,则f(O)=O.
定义1.8[14]设L1、L2是格蕴涵代数,规定(L1×L2,∨,∧,′,→,O,I)的运算如下:
∀x,y∈L1×L2,x=(x1,x2),y=(y1,y2),其中xi,yi∈Li(i=1,2).
1)x∧y=(x1∧x2,y1∧y2);
2)x∨y=(x1∨x2,y1∨y2);
4)x→y=(x1→x2,y1→y2);
5)O=(O,O),I=(I,I).
引理1.5[14]L1×L2在定义1.8 运算规定下构成一个格蕴涵代数.称L1×L2为格蕴涵代数L1、L2的乘积格蕴涵代数,简称为直积.
说明:上述引理1.1~1.2,1.4~1.5,定义1.1,1.5~1.8在文献[14]中第二章,本章系统介绍了格蕴涵代数的定义与基本性质,子代数、直积,同态与同构定理.
定义1.9[11]设A、B分别是格蕴涵代数L1、L2的模糊子集,∀x,y∈L1×L2,定义映射:
A×B:L1×L2→[0,1],(A×B)(x,y)=A(x)∧B(y),
则A×B是L1×L2的模糊子集,并称A×B是为A、B的直积.
2 格蕴涵代数的Ω-犹豫模糊子代数
定义2.1设X,Ω为非空给定集合,映射A:X×Ω→P([0,1])称为X的Ω-犹豫模糊集.记X上的全体Ω-犹豫模糊集为ΩHF[X].
定义2.2设A:L×Ω→P([0,1])∈ΩHF[L].如果∀x,y∈L,∀δ∈Ω,满足下列条件:
1)hA(O,δ)⊇hA(x,δ);
2)hA(x→y,δ)⊇hA(x,δ)∩hA(y,δ).
则称A是L的Ω-犹豫模糊子代数.记L的全体Ω-犹豫模糊子代数为ΩHFS[L].
定义2.3设A:L→P([0,1])∈HF[L].如果∀x,y∈L,满足下列条件:
1)hA(O)⊇hA(x);
2)hA(x→y)⊇hA(x)∩hA(y).
则称A是L的犹豫模糊子代数.记L的全体犹豫模糊子代数为HFS[L].
定理2.1设A:L×Ω→P([0,1])∈ΩHF[L].若A∈ΩHFS[L],则∀x,y∈L,∀δ∈Ω,有下列性质成立:
1)hA(I,δ)=hA(O,δ);
2)hA(x,δ)=hA(x′,δ);
3)hA(x∨y,δ)⊇hA(x,δ)∩hA(y,δ);
4)hA(x∧y,δ)⊇hA(x,δ)∩hA(y,δ).
定理2.1的证明1) ∀x∈L,∀δ∈Ω,首先,由于A∈ΩHFS[L],因此hA(O,δ)⊇hA(x,δ),取x=I,则hA(O,δ)⊇hA(I,δ);其次hA(I,δ)=hA(O→O,δ)⊇hA(O,δ)∩hA(O,δ)=hA(O,δ).
综上可得,hA(I,δ)=hA(O,δ).
2)∀δ∈Ω,∀x∈L,由于A∈ΩHFS[L],根据引理1.1,首先有:
hA(x,δ)=hA(I→x,δ)=hA(x′→I′,δ)=hA(x′→O,δ)⊇hA(x′,δ)∩hA(O,δ)=hA(x′,δ).其次,hA(x′,δ)=hA(x→O,δ)⊇hA(x,δ)∩hA(O,δ)=hA(x,δ).
因此可得,hA(x,δ)=hA(x′,δ).
3)∀δ∈Ω,∀x,y∈L,由A∈ΩHFS[L],根据引理1.1,可以得到hA(x∨y,δ)=hA((x→y)→y,δ)⊇hA(x→y,δ)∩hA(y,δ)⊇(hA(x,δ)∩hA(y,δ))∩hA(y,δ)=hA(x,δ)∩hA(y,δ).
4)∀δ∈Ω,∀x,y∈L,由于A∈ΩHFS[L],根据引理1.1和定理2.1的条件2)、3),有hA(x∧y,δ)=hA((x∧y)′,δ)=hA(x′∨y′,δ)⊇hA(x′,δ)∩hA(y′,δ)=hA(x,δ)∩hA(y,δ).
定理2.2设A:L×Ω→P([0,1])∈ΩHF[L].A∈ΩHFS[L]当且仅当∀γ∈(0,1],R(A,γ)Ω≠∅是L的子代数.其中定义
R(A,γ)Ω={x∈L|hA(x,δ)⊇γ,∀δ∈Ω}.
定理2.2的证明“⟹” ∀δ∈Ω,由于R(A,γ)Ω≠φ,因此∃x0∈R(A,γ)Ω,即hA(x0,δ)⊇γ.又由于A∈ΩHFS[L],因此hA(O,δ)⊇hA(x,δ)⊇γ,即O∈R(A,γ)Ω;如果x∈R(A,γ)Ω并且y∈R(A,γ)Ω,那么有hA(x,δ)⊇γ和hA(y,δ)⊇γ成立.
即hA(x→y,δ)⊇hA(x,δ)∩hA(y,δ)⊇γ,hA(x→y,δ)⊃γ,因此x→y∈R(A,γ)Ω.综上可得,R(A,γ)Ω≠∅是L的子代数.
“⟸”∀δ∈Ω,假设∃x0∈L,我们有hA(O,δ)⊂hA(x0,δ),令hA(O,δ)⊂γ⊆hA(x0,δ),因此R(A,γ)Ω≠φ.由于R(A,γ)Ω是L的子代数,即O∈R(A,γ)Ω,因此hA(O,δ)⊇γ,这与hA(O,δ)⊂γ产生矛盾.所以∀δ∈Ω,∀x∈L,hA(O,δ)⊇hA(x,δ).

定理2.3设A:L×Ω→P([0,1])∈ΩHF[L],A∈ΩHFS[L]当且仅当∀γ∈(0,1],R(A,γ)⊃Ω≠φ是L的子代数. 其中定义
R(A,γ)⊃Ω={x∈L|hA(x,δ)⊃γ,∀δ∈Ω}.
定理2.3的证明同定理2.2的证明.
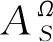

记L的全体Ω-犹豫模糊特征函数为ΩHFCF[L].
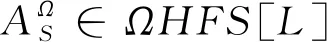
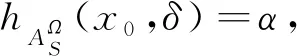
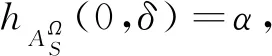
定理2.5设A:L×Ω→P([0,1])∈ΩHF[L].A∈ΩHFS[L]当且仅当Aδ∈HFS[L],定义Aδ:L→P([0,1]),∀x∈L,∀δ∈Ω,其中hAδ(x)=hA(x,δ).
定理2.5的证明“⟹”若A∈ΩHFS[L],则∀x,y∈L,∀δ∈Ω.首先hAδ(0)=hA(0,δ)⊇hA(x,δ)=hAδ(x);其次,hAδ(x→y)=hA(x→y,δ)⊇hA(x,δ)∩hA(y,δ)=hAδ(x)∩hAδ(y).因此可得,Aδ∈ΩHFS[L].
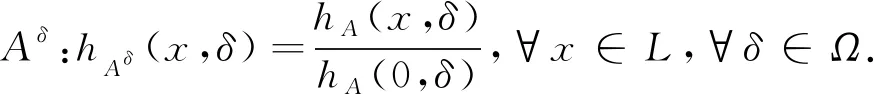
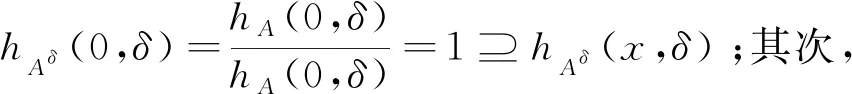
定理2.7设A、B∈ΩHFS[L],则A∩B∈ΩHFS[L].
定理2.7的证明若A、B∈ΩHFS[L],则∀δ∈Ω,∀x,y∈L.首先hA∩B(O,δ)=hA(O,δ)∩hB(O,δ)⊇hA(x,δ)∩hB(x,δ);其次hA∩B(x→y,δ)=hA(x→y,δ)∩hB(x→y,δ)⊇(hA(x,δ)∩hA(y,δ))∩(hB(x,δ)∩hB(y,δ))=(hA(x,δ)∩hB(x,δ))∩(hA(y,δ)∩hB(y,δ))=hA∩B(x,δ)∩hA∩B(y,δ).
即A∩B∈ΩHFS[L].

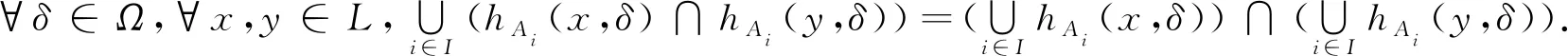
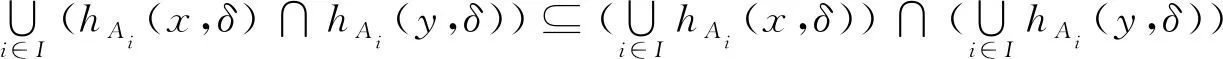



设A∈ΩHF[X],0≤k≤1,∀x∈X,δ∈Ω,定义A∪k,A∩k为:
hA∪k(x,δ)=hA(x,δ)∪k,hA∩k(x,δ)=hA(x,δ)∩k.
定理2.9若A∈ΩHFS[L],则A∩k∈ΩHFS[L].
定理2.9的证明若A∈ΩHFS[L],则∀δ∈Ω,x,y∈L.首先,hA∩k(O,δ)=hA(O,δ)∩k⊇hA(x,δ)∩k=hA∩k(x,δ);其次,hA∩k(x→y,δ)=hA(x→y,δ)∩k⊇(hA(x,δ)∩hA(y,δ))∩k=(hA(x,δ)∩k)∩(hA(y,δ)∩k)=hA∩k(x,δ)∩hA∩k(y,δ).因此可得A∩k∈ΩHFS[L].
定理2.10若A∈ΩHFS[L],则A∪k∈ΩHFS[L].
定理2.10的证明若A∈ΩHFS[L],则∀δ∈Ω,x,y∈L.首先,hA∪k(O,δ)=hA(O,δ)∪k⊇hA(x,δ)∪k=hA∪k(x,δ);其次,hA∪k(x→y,δ)=hA(x→y,δ)∪k⊇(hA(x,δ)∩hA(y,δ))∪k=(hA(x,δ)∪k)∩(hA(y,δ)∪k)=hA∪k(x,δ)∩hA∪k(y,δ).
综上可得,A∪k∈ΩHFS[L].
3 格蕴涵代数的Ω-犹豫模糊子代数的同态与直积
定理3.1设L1、L2是格蕴涵代数,映射f:L1→L2为格蕴涵满同态映射.若A∈ΩHFS[L1],则f(A)∈ΩHFS[L2].
定理3.1的证明∀y1,y2∈L2,因为映射f:L1→L2为格蕴涵满同态映射,所以∃x1,x2∈L1,使得f(x1)=y1,f(x2)=y2,且f(O)=O,从而∀δ∈Ω.
定义:
hf(A)(y,δ)=∪{hA(x,δ)|f(x)=y,δ∈Ω}.
首先hf(A)(O,δ)=∪{hA(x,δ)|f(x)=O,δ∈Ω}=∪{hA(O,δ)|f(O)=O,δ∈Ω}⊇∪{hA(x1,δ)|f(x1)=y1,δ∈Ω}=hf(A)(y1,δ);其次,hf(A)(y1→y2,δ)=∪{hA(x,δ)|f(x)=y1→y2,δ∈Ω}⊇∪{hA(x1→x2,δ)|f(x1→x2)=y1→y2,δ∈Ω}=∪{hA(x1→x2,δ)|f(x1)→f(x2)=y1→y2,δ∈Ω}⊇∪{hA(x1,δ)|f(x1)=y1,δ∈Ω}∩∪{hA(x2,δ)|f(x2)=y2,δ∈Ω}=hf(A)(y1,δ)∩hf(A)(y2,δ).综上可得,f(A)∈ΩHFS[L2].
定理3.2设L1、L2是格蕴涵代数,映射f:L1→L2为格蕴涵同态映射,若B∈ΩHFS[L2]当且仅当f-1(B)∈ΩHFS[L1].
定理3.2的证明“⟹” 若B∈ΩHFS[L2],则∀y1,y2∈L1,∀δ∈Ω.
定义:
hf-1(B)(y,δ)=hB(f(y),δ),δ∈Ω,
首先,hf-1(B)(O,δ)=hB(f(O),δ)⊇hB(f(y1),δ)=hf-1(B)(y1,δ);其次,hf-1(B)(y1→y2,δ)=hB(f(y1→y2),δ)=hB(f(y1)→f(y2),δ)⊇hB(f(y1),δ)∩hB(f(y2),δ)=hf-1(B)(y1,δ)∩hf-1(B)(y2,δ).
于是,f-1(B)∈ΩHFS[L1].
“⟸”若f-1(B)∈ΩHFS[L1],∀y1,y2∈L2,因为f:L1→L2为格蕴涵满同态映射,所以∃x1,x2∈L1,使得f(x1)=y1,f(x2)=y2,且f(O)=O.因此∀δ∈Ω,首先,hB(O,δ)=hB(f(O),δ)=hf-1(B)(O,δ)⊇hf-1(B)(x1,δ)=hB(f(x1),δ)=hB(y1,δ);其次,hB(y1→y2,δ)=hB(f(x1)→f(x2),δ)=hB(f(x1→x2),δ)=hf-1(B)(x1→x2,δ)⊇hf-1(B)(x1,δ)∩hf-1(B)(x2,δ).
综上可得,B∈ΩHFS[L2].
定义3.1设A∈ΩHF[L1]、B∈ΩHF[L2],定义映射∀(x1,x2)∈L1×L2,∀δ∈Ω,A×B:[L1×L2]×Ω→P([0,1]),其中
hA×B((x,y),δ)=hA(x,δ)∩hB(y,δ),
则称A×B为L1×L2的Ω-犹豫模糊子集,并称A×B为A、B关于Ω的直积.
记L1×L2上的全体Ω-犹豫模糊子集为ΩHF[L1×L2].
定理3.3设A∈ΩHFS[L1]、B∈ΩHFS[L2],则A×B∈ΩHFS[L1×L2].
定理3.3的证明若A∈ΩHFS[L1]、B∈ΩHFS[L2],首先,∀(x1,x2)∈L1×L2,∀δ∈Ω,hA×B((O,O),δ)=hA(O,δ)∩hB(O,δ)⊇hA(x,δ)∩hB(x,δ)=hA×B((x,y),δ);其次,∀(x1,y1),(x2,y2)∈L1×L2,∀δ∈Ω,hA×B((x1,y1)→(x2,y2),δ)=hA×B((x1→x2,y1→y2),δ)=hA(x1→x2,δ)∩hB(y1→y2,δ)⊇(hA(x1,δ)∩hA(x2,δ))∩(hB(y1,δ)∩hB(y2,δ))=(hA(x1,δ)∩hB(y1,δ))∩(hA(x2,δ)∩hB(y2,δ))=hA×B(x1,y1)∩hA×B(x2,y2).综上可得,A×B∈ΩHFS[L1×L2].
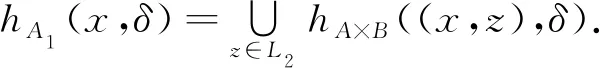
定理3.4若A×B∈ΩHFS[L1×L2],则A1(x,δ)∈ΩHFS[L1],B1(y,δ)∈ΩHFS[L2].
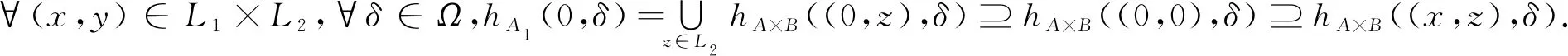

综上可得,A1(x,δ)∈ΩHFS[L1].
类似地,可得B1(y,δ)∈ΩHFS[L2].
