基于非线性干扰观测器的二阶欠驱动系统轨迹跟踪控制

徐增勇 程 赟 韦延方

(河南交通职业技术学院汽车学院 河南 郑州 450000)2(河南理工大学电气工程与自动化学院 河南 焦作 454000)

0 引 言

欠驱动系统是一类控制输入少于系统自由度的系统[1-2]。由于它具有减少能量消耗、简化控制器设计和增强控制系统对执行器故障的容错率的优点，被广泛应用于实际工业和生活领域[3]，比如近期比较流行的四旋翼无人机和平衡小车都属于欠驱动系统。同时，由于欠驱动系统具有强非线性、强耦合等特性，可以用于验证研究人员设计的控制策略的有效性，也被广泛应用于理论研究和教学研究[4]，许多高校将经典的小车倒立摆欠驱动系统作为自动化学科的实验教学器材。在过去一段时间，欠驱动系统的主流控制方法还是PID[5]、极点配置和LQR[6]，虽然上述方法能很好地完成控制任务，但是线性化的前提导致了控制器的鲁棒性较差，系统的建模误差、外部扰动和非线性特性对控制器的性能影响较大，甚至会导致系统不稳定。随着控制理论的不断向前发展，以及人们对控制器性能的要求越来越高，系统的不确定性成为了高性能控制器设计过程中不可忽视的问题，系统的模型也不是完全已知，甚至完全未知。为了应对越来越复杂的控制环境和越来越严格的控制条件，许多优秀的控制方法被应用到欠驱动系统中，控制器的鲁棒性作为控制系统关键性能指标受到广泛的重视。自适应控制方法[7]由于具有根据系统动态来自适应调节控制器参数的特点被认为是一种解决复杂非线性系统的有效控制策略，但自适应控制方法在处理系统参数扰动和外部扰动的能力上显得捉襟见肘了。近些年来，很多研究学者将人工智能的方法引入欠驱动系统的控制中来，如神经网络[8]、模糊系统[9]、深度学习等。由于神经网络和模糊系统具有逼近任意非线性方程的能力[10]，所以被广泛应用到欠驱动系统控制器设计中。常见的方法就是利用神经网络和模糊系统来估计系统的不确定性，通过与其他控制策略结合来设计出鲁棒性强的控制器。但是，这些万能逼近器的应用会加大控制器的复杂度而导致应用的困难。滑模控制(Sliding Mode Control,SMC)作为流行的控制策略用于处理系统不确定性问题和欠驱动系统鲁棒控制设计。滑模控制策略具有对参数扰动和外部扰动不敏感、响应迅速和易于实际应用的优点[11]。干扰观测器(Disturbance Observer,DO)作为观测器的扩展用法，被用于估计系统的扰动，因此受到了广泛关注。为了处理系统的确定性，基于干扰观测器的滑模控制策略被应用到欠驱动系统的控制问题中。文献[12]通过严格反馈将欠驱动系统转换成标准级联形式，从而设计了基于非线性干扰观测器的滑模控制策略。但是文献中的转换方法并不适用于Ⅱ型欠驱动系统[2]。文献[13]针对带有非匹配扰动的机器人欠驱动系统设计了基于高阶干扰观测器的滑模控制方法。本文利用文献[14]提出的非线性干扰观测器(Nonlinear Disturbance Observer,NDO)来处理系统中的未建模误差、参数扰动和外部扰动。这种新型观测器具有结构简单、参数易于设计的优点，同时避免了需要知道扰动先验知识的缺点。将其与分层滑模控制器结合，可以设计出强鲁棒性的控制器。控制系统的稳定性也通过Lyapunov方法进行了严格的理论分析，使其能更好地应用于不同的二阶欠驱动系统。最后，通过对比仿真实验证明了本文提出的控制策略在满足控制目标的前提下，具有很好的鲁棒性。

1 系统描述

根据拉格朗日方程[2],2阶欠驱动系统的动态方程表示如下：

(1)

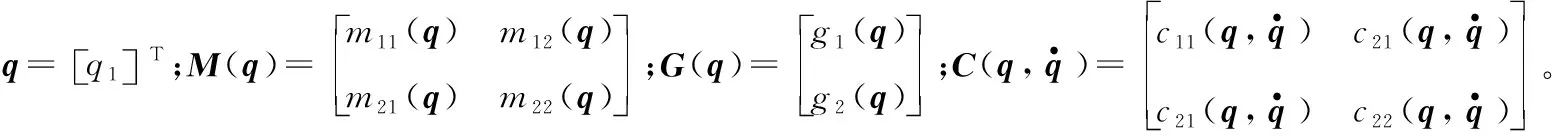
(2)

式中：Δf1(x)、Δf2(x)、Δb1(x)和Δb2(x)是系统的未建模误差和参数扰动；d1(t)和d2(t)代表系统的外部扰动；u为系统的控制输入。

首先，系统跟踪误差如下：

(3)

式中：x1d和x3d是期望的跟踪轨迹。

根据式(2)和式(3)可以得到如下的误差动态方程：

(4)

式中：d1all=Δf1+Δb1u+d1和d2all=Δf2+Δb2u+d2为系统的不确定性扰动总和，本文将利用NDO补偿控制系统的扰动总和。为了完成跟踪控制目标，我们做出如下符合实际情况的假设。

2 控制器设计

本文引用文献[14]提出的观测器来估计和补偿式(4)中不确定性扰动总和，从而提高控制器的鲁棒性。

引理1根据式(2)和假设2，用于估计不确定扰动总和d1all和d2all的观测器形式如下：

(5)

(6)

(7)

(8)

定义如下两个子滑模面：

(9)

式中：c1和c2为需要设计的正参数。然后定义如下的总滑模面：

s=cs1+s2

(10)

式中：c是需要设计的正参数。根据式(4)和式(9)，总滑模面的导数如下：

d2all+(c3b1+b2)(ueq1+ueq2+uw)

(11)

式中：控制率u=ueq1+ueq2+uw,ueq1和ueq2表示滑模控制的等效控制率，uw为切换控制率。

系统的等价控制率设计如下：

(12)

ηsgn(s)+ks)/(c3g1+g2)

(13)

图1为控制器的设计结构框图。

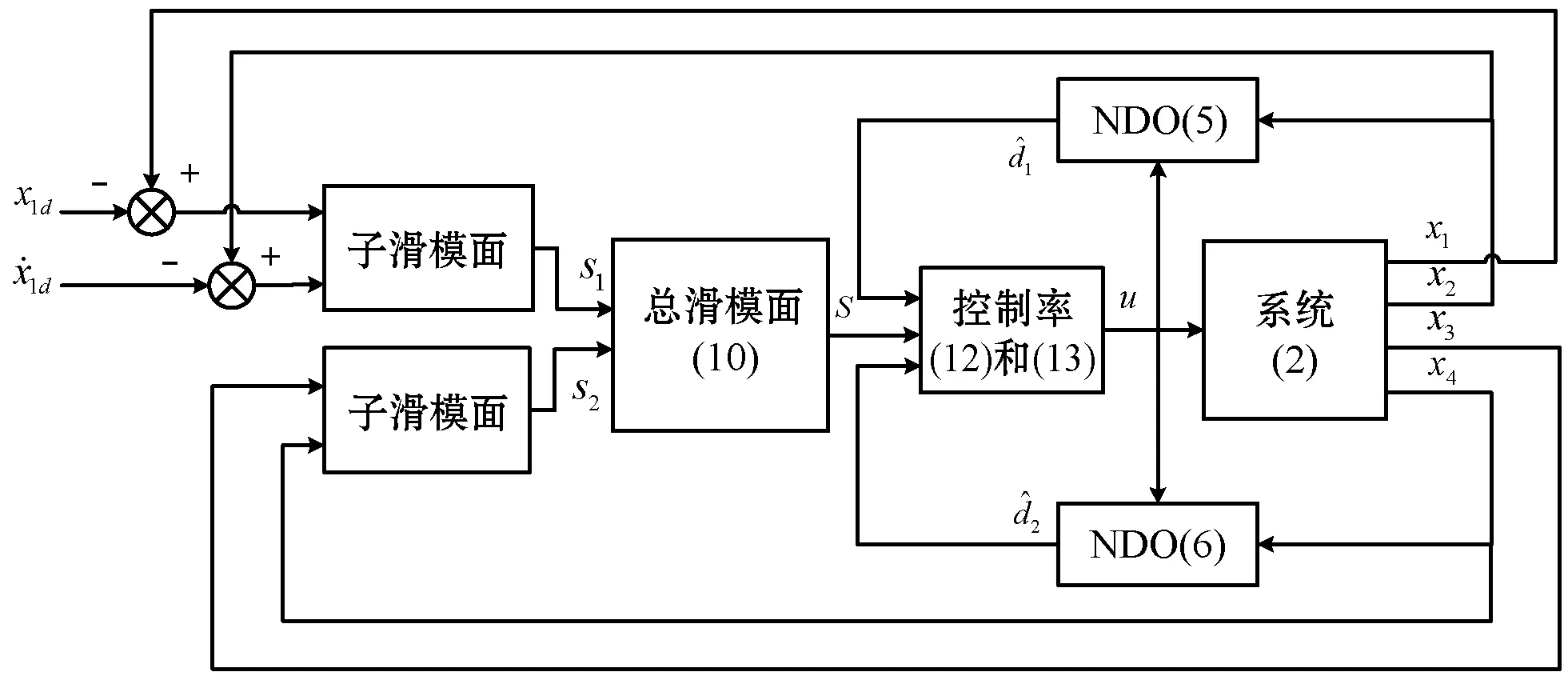
图1 基于非线性干扰观测器的分层滑模控制器设计框图

定理1对式(2)描述的欠驱动系统，如果滑模面的设计为式(12)和式(13)，并且控制器的参数设计满足：

k>0,η>c3μ1+μ2

(14)

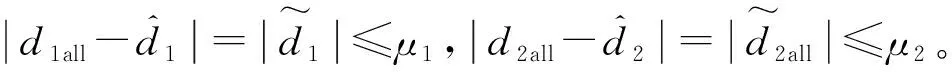
证明:选择如下的Lyapunov函数:

V=s2/2

(15)

根据式(4)和式(9)，将式(15)求导可得：

c2x4+f2+d2all+(c3b1+b2)u)

(16)

然后将式(12)和式(13)代入式(16)则有：

-(η-c3σ1-σ2)|s|-ks2

(17)

将式(17)两边进行积分操作，则有：

(18)

然后：

(19)

由于Lyapunov方程满足V(t)≥0,所以：

(20)

然后：

(21)

根据Barbalat引理[16]有：

(22)

因为控制器参数选择满足式(14)，所以：

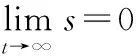
(23)

定理1证明完毕。

3 仿真研究

为了证明提出的控制策略的有效性，本节将经典欠驱动系统小车倒立摆[2]作为仿真对象，图2为小车倒立摆的系统结构。其中：x=x1；θ=x3；在仿真研究中，控制对象的物理参数选择如下：M=1.2 kg，m=0.15 kg，l=0.5 m，g=9.8 N/kg；系统的初始状态为x=[0,0,0,0]T。为了证明控制器的优越性，选择文献[17]和文献[5]进行对比仿真。为了方便表达，本文提出的控制器用N-SMC表示，将文献[17]的控制器用A-SMC表示，将文献[5]提出的控制策略用D-PID表示。三种控制器的参数如表1-表3所示。

图2 小车倒立摆系统示意图

表1 N-SMC设计参数

表2 A-SMC设计参数

表3 D-PID设计参数

注意1为了验证控制器的有效性，对比仿真实验中N-SMC和A-SMC滑模面参数的选择相同，其中：λ1和λ1是自适应律参数；PID1和PID2分别为小车位置和摆杆摆动闭环的控制参数。

在仿真实验中，控制器设计目标是使小车跟踪期望的跟踪轨迹0.5sin(0.5t)，并且摆杆在一定范围内摆动保持竖直状态。

仿真实现分为两种情况，每种情况对应一种不同的扰动形式。

情况1在仿真进行到15 s的时候，输入端加入2sin(t)的扰动量。仿真结果如图3-图5所示。

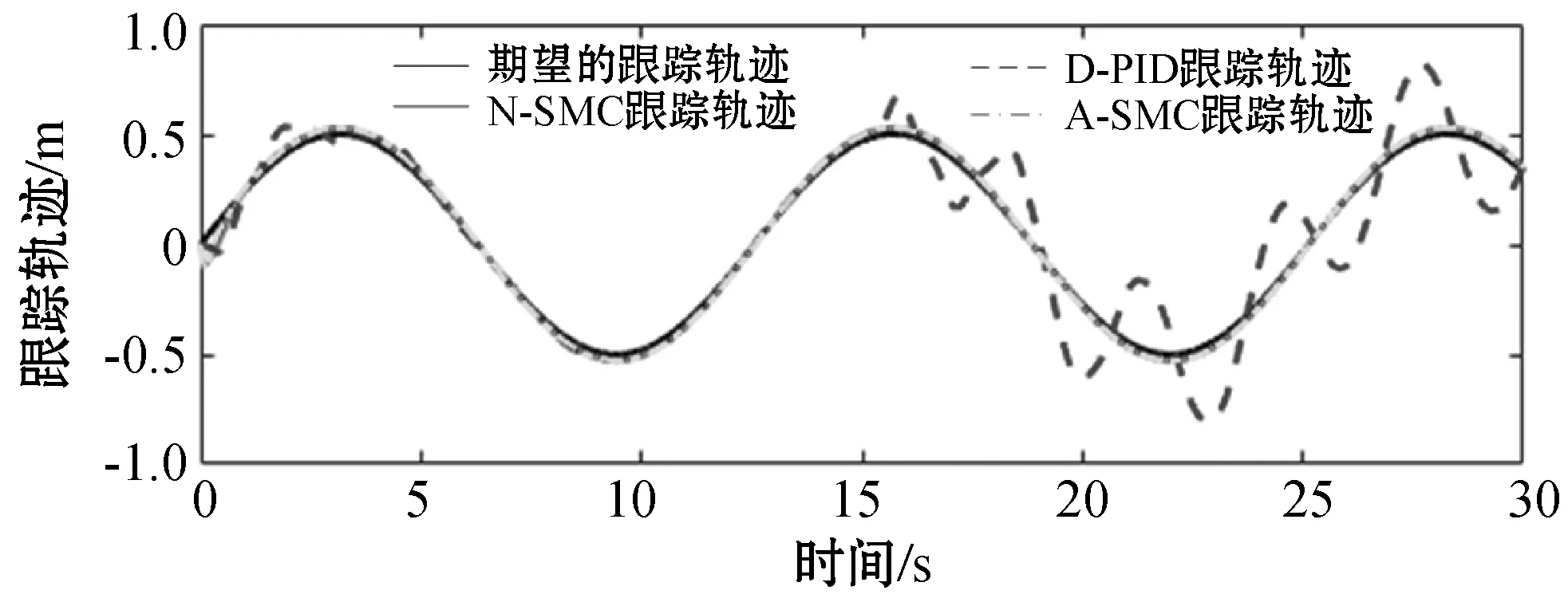
图3 带有输入扰动的跟踪效果

图4 带有输入扰动的跟踪误差

图5 带有输入扰动的摆杆摆动角度

可以看出，三种控制器都能很好地跟踪期望的轨迹并保持摆杆处于竖直状态。但是，在15 s时加入输入扰动后，D-PID的跟踪误差和摆杆摆动角度大幅度增加。而N-SMC和A-SMC基本没有受到影响，结果说明本文提出的控制器对输入扰动具有很好的抑制作用。

情况2本次实验用于测试控制系统对参数扰动的抗扰能力，在仿真进行到15 s的时候，将系统的物理参数M从1.2 kg变成5 kg。仿真结果如图6-图8所示。

图6 带有参数扰动的跟踪效果

图7 带有参数扰动的跟踪误差

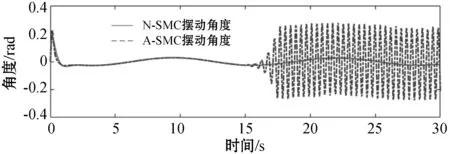
图8 带有参数扰动的摆杆摆动角度

注意2在参数扰动仿真实验中，D-PID控制器在较大参数扰动下已经发散从而影响控制效果的对比，故没有将D-PID的控制结果放入仿真结果图6-图8中。

从上述的仿真结果图可以看出，A-SMC控制器在加入大的参数扰动后跟踪误差出现了高频大幅度振动，摆杆的摆动角度也出现了高频大幅振动，而N-SMC基本没有受到影响，仿真结果证明了本文提出的控制器具有很好的鲁棒性。

4 结 语

本文针对二阶欠驱动系统跟踪控制问题提出一种基于非线性干扰观测器的分层滑模控制策略。通过引用一种新型非线性干扰观测器用于补偿系统的不确定性扰动，结合分层滑模控制策略，设计出一种具有强鲁棒性的控制器。对比仿真表明，本文设计的控制器对外部扰动和参数扰动具有很好的抑制作用。同时，通过严格的Lyuapnov稳定性分析，证明了控制系统闭环稳定性。