多模态高维数据关联分析的联合协同回归模型

王凯明 李荣鹏 肖玉柱 宋学力

(长安大学理学院 陕西 西安 710064)

0 引 言

在大数据时代，伴随着信息技术的快速发展和数据获取手段的多样化，产生了大量的多模态高维数据。多模态高维数据的关联分析实现模态间信息的互补，可提高数据的使用价值。然而在进行多模态高维数据关联分析时，对不同模态数据进行简单的整合并不能保证挖掘任务的有效性，且经常出现过拟合现象。因此，研究有效的模型在防止过拟合的同时实现多模态数据的关联分析，然后得到多模态高维数据中的重要信息，支撑后续的决策、预测，具有重要的现实意义，也是现阶段大数据研究关注的重要课题之一[1-2]。

在统计学习中,线性回归(Linear Regression,LR)和典型相关分析(Canonical Correlation Analysis,CCA)是研究变量间关系的两个常用统计模型。其中，线性回归主要针对单模态数据,研究变量组与响应变量之间的线性依赖关系；而典型相关分析主要针对两模态数据,通过典型变量的相关性来刻画变量之间相关性[3]。然而，现实任务中的单模态或者多模态数据，经常会存在样本特征维度(或属性维度)远大于样本数的现象，这会导致统计学习的严重过拟合或者维数灾难问题，所以需要从样本的高维特征空间里提取或者选择较少的“重要”的特征来解决或者缓解过拟合问题以及维数灾难问题。利用某些向量范数(如l1范数)的稀疏性能，通过对目标进行正则惩罚来实现特征选择，是近年来研究者们常用的方法[4-5]。稀疏线性回归(Sparse Linear Regression,SLR)[4]和稀疏典型相关分析(Sparse Canonical Correlation Analysis,SCCA)[5]就是基于这个思想发展的具有特征提取功能和统计分析功能的新模型。针对已知响应变量数据的多模态数据，兼顾响应变量的监督作用和两模态数据的关联性背景，结合SLR与SCCA进行多模态数据的特征选择[6-7]可以实现有监督的多模态数据特征提取以及相关关系研究。文献[6]组合了SLR与SCCA模型得到协同回归模型(Collaborative Regression,CoReg)，并用于乳腺癌多模态数据的特征选择，得到与乳腺癌多模态数据及其响应变量保持一致的重要特征。文献[7]组合上述两个模型得到多任务协同回归模型(Multi-Task Collaborative Regression,MT-CoReg)，并应用于精神分裂症多模态数据的特征选择，该模型对变量进行分组，在多模态数据之间，以及多模态数据与响应变量之间进行“强迫”回归,提高了特征选择的准确度。值得注意的是，在CoReg模型和MT-CoReg模型中均假设所有样本数据分布规律相同，然而实际问题中，数据往往来自不同状态的样本，并且不同状态的样本数据之间存在显著的差异[8](例如：来自不同疾病状态病人的数据分布不同；来自不同年龄段个体的数据分布亦可能存在显著差异)。因此，在模型中考虑不同类样本数据的分布差异性更适合实际数据的分布规律，也有利于类相关特征选择。一种简单的想法就是对样本分类，对每一类样本单独处理。这样可进行类相关信息的选择，但是导致可用的样本数量较少，增加了学习难度并且容易忽略不同类样本数据之间的共同信息的选择，使得其实际应用受到限制。因此，本文考虑对不同种类样本进行联合分析，通过多类多模态数据信息的互补实现类相关特征选择。

针对上述问题，本文考虑Fused lasso[9]的融合作用，在文献[6]中模型的基础上加入Fused lasso惩罚构建本文的模型。文献[9]中Fused lasso惩罚通过对回归系数中相邻元素之差进行l1惩罚达到回归系数融合的目的，可保证回归系数具有光滑性。本文考虑对不同类样本的典型向量进行Fused lasso惩罚，使得不同的典型向量之差具有稀疏性，不同典型向量中相同坐标分量之间具有光滑性。就是通过Fused lasso惩罚实现了K类样本的联合。

本文首先构建联合协同回归模型(Joint Collaborative Regression,Joint-CoReg)，其主要思想为：根据先验信息(如年龄、疾病状态等)将样本分为K类,通过协同回归模型进行变量之间以及变量与标签之间的相关性分析，然后使用Fused lasso实现K类样本之间的联合作用，最后使用l1范数得到类相关的稀疏典型向量。求解其中一模态数据的一个典型向量，另一模态数据的K个不同典型向量有两方面的原因。一方面，考虑模型在实际问题中的应用。例如影像遗传学研究中，通常采集脑图像数据和基因数据来研究某些疾病(如精神分裂症、阿尔茨海默病等)，研究人员希望找到与疾病相关的共同病变脑区和导致不同疾病状态的不同致病基因[10]，此时共同病变脑区和不同致病基因正好分别对应我们模型中的一模态数据的一个典型向量和另一模态数据的K个不同典型向量。另一方面，限制其中一模态数据属于共同类克服了多类样本直接组合的数据不匹配问题，提高了模型求解的稳定性。

1 方 法

1.1 稀疏回归模型和稀疏典型相关分析模型

设X=[X1；X2；…；Xn]与Z=[Z1；Z2；…；Zn]为已标准化的两模态样本数据，其中Xi∈R1×p，Zi∈R1×q表示样本的第i个分量数据，i=1,2,…,n；Y∈Rn为样本的响应变量数据。

数据X与其响应变量数据Y之间的回归模型可以表示为：

在Xω和Zν方差确定的条件下，两模态数据X和Z的典型相关分析模型可以表示为：

然而，对于常见的高维度、小样本的问题，以上模型通常会出现过拟合现象，导致模型无法求解。文献[5,8]考虑l1范数的稀疏作用，在上述模型中加入l1范数稀疏惩罚，构造基于稀疏惩罚的回归模型和典型相关分析模型。

数据X与其响应变量数据Y之间的稀疏回归模型可以表示为：

式中：λ为待定参数。通过求解稀疏回归系数ω挖掘数据X和Y之间的稀疏线性关系。

在Xω和Zν方差确定的条件下，两模态数据X和Z的稀疏典型相关分析模型可以表示为：

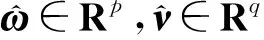
文献[6]结合稀疏回归模型和稀疏典型相关分析模型提出协同回归模型，其目标函数如下：

该模型在响应变量数据Y的监督下得到两模态数据X和Z之间具有最大相关性的稀疏典型向量，但是忽略了不同类样本数据的分布信息性，增加了类相关特征选择的难度。

1.2 联合协同回归模型

考虑包含多类样本的两模态数据X∈Rn×p，Z∈Rn×q。按样本种类将数据分为X=[X1；X2；…；XK],Z=[Z1；Z2；…；ZK],Xk∈Rnk×p,Zk∈Rnk×q表示第k类样本,k=1,2,…,K。对X、Z、Y进行联合协同回归，建立目标函数：

(1)

式中：ω∈Rp×1,υk∈Rq×1，k=1,2，…,K,分别是X和Zk对应的典型向量,a、λ1、λ2为可调参数，λ1、λ2用于调节ω、υk的稀疏程度。通过求解目标函数分别得到关于X和Zk(k=1,2,…,K)的典型相关变量。

不同类样本之间的联合，使用以下Fused lasso惩罚项实现：

Fused lasso惩罚项对不同类的典型向量之差进行稀疏惩罚，保证不同典型向量的相同分量之间具有光滑性。通过Fused lasso惩罚和l1范数惩罚得到类相关稀疏典型向量。参数a控制υk(k=1,2,…,K)之间的融合程度。特别地,当a=0时,各类样本之间无融合作用，此时模型等价于对K类样本分别协同回归；当a=∞时，所有类别的样本被视为一类，其对应的典型向量υk完全相同，此时模型等价于将K类样本作为整体协同回归。

1.3 模型优化算法

为了保证联合协同回归模型(1)解的唯一性，我们对典型向量ω、νk的范数(或长度)加以约束，将优化问题(1)转化为以下约束优化问题：

(2)

将式(2)中的l2范数按照向量内积展开，去掉展开式中常数项(常数项不含决策变量，不影响优化问题求解最小值)，优化问题转化为如下形式：

(3)

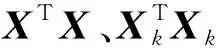
(4)

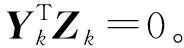
(5)

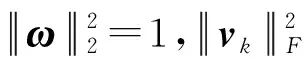
(6)

(7)

式中：c为非负参数,当c=0时标签数据变为0，此时模型只进行协变量(多模态数据)之间的相关性分析，模型相当于联合典型相关分析模型[8]。随着c的增大，T中绝对值较大的元素变化幅度较大。因此在参数选择中选择合适的c有利于样本中较重要特征的选择[14]。

由以上推导,式(2)的求解可以转化为式(5)求解(当K=2时，使用式(7)代替式(5))。式(5)(或式(7))中ω、vk为决策变量，固定ω，式(5)(或式(7))为另一决策变量vk的凸函数，反之亦然。可以使用块坐标下降法对式(5)(或式(7))分式(8)-式(9)两步进行迭代求解：

(8)

(9)

为求解式(8)和式(9),引入如下引理。

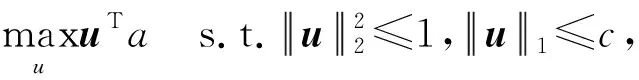
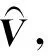
(10)

(11)

式(10)为Fused lasso信号逼近的一种特殊情况。通过融合、稀疏和正则化三步对其进行求解，由文献[15]得到式(10)求解算法。优化问题(8)和问题(9)可分别应用引理1和引理2得以求解。下面给出联合协同回归模型详细求解算法[6,13]，如算法1所示。

算法1Joint-CoReg算法

输入:标准化数据:X∈Rn×p,Xk∈Rnk×p,Zk∈Rnk×q,Y∈Rn×1，可调参数a,λ1,λ2

输出:ω和υk

(1) 初始化ω∈Rp×1,υk∈Rq×1,k=1，2，…，K

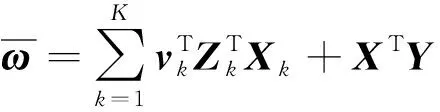
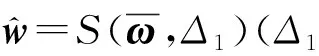
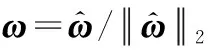
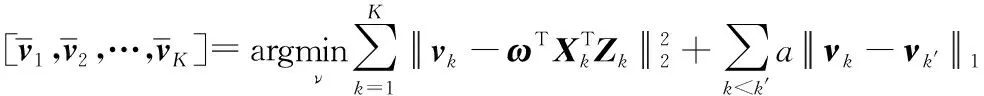
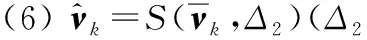
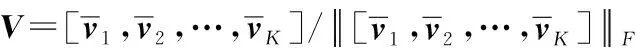
(9) 重复步骤(2)-步骤(8)，直到算法收敛

1.4 模型的应用

多模态高维数据关联分析模型，在防止高维数据过拟合的同时，通过模态间信息的互补挖掘数据中隐藏的价值，具有重要的现实意义。本文建立联合协同回归模型，该模型可有效地防止过拟合，且进行多模态数据的关联分析，最终得到数据的重要信息。数据的重要信息在模型中则表现为稀疏典型变量中非零元素。通过数据的重要信息可以进一步进行分类、预测等诸多任务，其应用范围非常广泛。

为了验证本文模型得到的重要信息有效性，将模型用于特征选择，直接对比本文模型求得的实验结果和真值，二者越接近说明模型越有效。

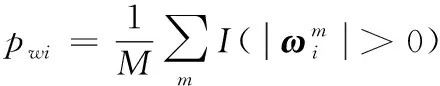
式中：I为示性函数；m1为给定阈值；Sωi为选择特征的集合。对于Zk的典型向量,给定阈值m2，利用同样的方法进行特征选择。

2 实验与结果分析

2.1 生成模拟数据

考虑包含两类样本的两模态数据,每一类样本包含n个样例。数据构造方法与文献[5,8]中数据构造方法相类似。首先构造潜变量hk={hki|i=1,2,…,n},hk∈Rn×1,hki～N(μk,δ)(k=1,2,…,K),不同的μk来构造不同类别的样本；其次产生X和Yk的典型向量α和βk,α∈R1×p,βk∈R1×q,α和βk中分别包含m和r个非零的元素，其中非零元素为需要选择的特征；最后得到Xk和Zk：Xk=hkα，Zk=hkβk。不失一般性，此处给定两类样本，且μ1=-1,μ2=1,n=100，特征数p=q=500，典型向量的稀疏度m=r=150。

2.2 参数选择

该模型有四个可调参数λ1、λ2、a、c(两类样本的情况考虑参数c)，其中λ1,λ2控制典型向量的稀疏程度，a控制各Zk的典型向量的相似程度，c的大小反映响应变量数据的重要程度。为了保证模型的稳定性,本文分两步进行参数选择：第一步，根据文献[16]指出的参考解的稀疏程度进行参数选取。本文根据需要保留的特征数量指导λ1、λ2的选取。第二步：在参数λ1、λ2确定的情况下，给定a和c的备选区间[10-2,10-1,100,101,102]，使用自助法(bootstrapping)从已有的样本中产生M组不同的训练样本和测试样本，用网格搜索的方法，选择使得测试集和训练集相关系数平均绝对误差取得最小值的一组参数a和c，作为参数a和c的最优值，模型使用的参数值在实验部分均给出。测试集和训练集相关系数平均绝对误差计算公式如下：

式中：corrtrain为训练集上的Pearson相关系数，corrtest为测试集上的Pearson相关系数。

2.3 实验结果分析

联合协同回归模型在保证典型变量之间有较高相关性的前提下通过典型向量选择重要特征，本文在实验部分从典型变量的相关性和特征选择准确率两方面验证模型的有效性。其中典型变量之间的相关性使用Pearson相关系数描述,特征选择准确性使用ROC曲线来描述。给定特征向量的稀疏度(λ1、λ2给定),研究参数a和c对典型变量的相关性和特征选择准确率的影响(不同参数a和c将模型转化为其他模型，相当于对比实验)。

表2给定最优参数λ1、λ2、a，研究参数c的变化对典型变量相关性的影响，c分别取值0、50、100、150。实验结果表明，c取值为50和100时相关性略高于c取值为0和150时的相关性,但是在四个取值下所得相关性相差不大。表3给定参数λ1、λ2、c，研究参数a的变化对典型变量相关性的影响。a分别取值0、10、20、1 000，实验结果表明a取值为0时取得最大的相关性,在a的四个取值下所得相关性相差不大。所以，表1和表2表明特征选择稀疏度给定(λ1、λ2给定)的情况典型变量相关性对参数a、c不敏感，说明本文模型可以保证多模态数据之间(协变量之间)的相关性。

表1 参数c对数据相关性影响对比

表2 参数a对数据相关性影响对比

ROC曲线反映了在不同参数下模型选择特征的准确度，其中ROC曲线越靠近(0,1)点，说明特征选择准确率越高。图1给定最优参数λ1、λ2、a,研究参数c的变化对样本数据X的特征选择准确性的影响,ROC图像表明c=50和c=100时模型选择特征的准确度明显高于c=50和c=150时特征选择的准确性。c=0时响应变量的取值为零,此时去掉了表型变量数据对特征选择影响，特征选择准确率降低,由此说明在表型变量数据的监督下可提高模型特征选择的准确性；c=100时加大了响应变量数据的作用,减小了协变量的影响,降低了Joint-CoReg模型特征选择的准确率。图1说明响应变量数据在一定程度上影响特征选择的准确率，对响应变量数据给定合适的权重可以提高模型特征选择的准确率。

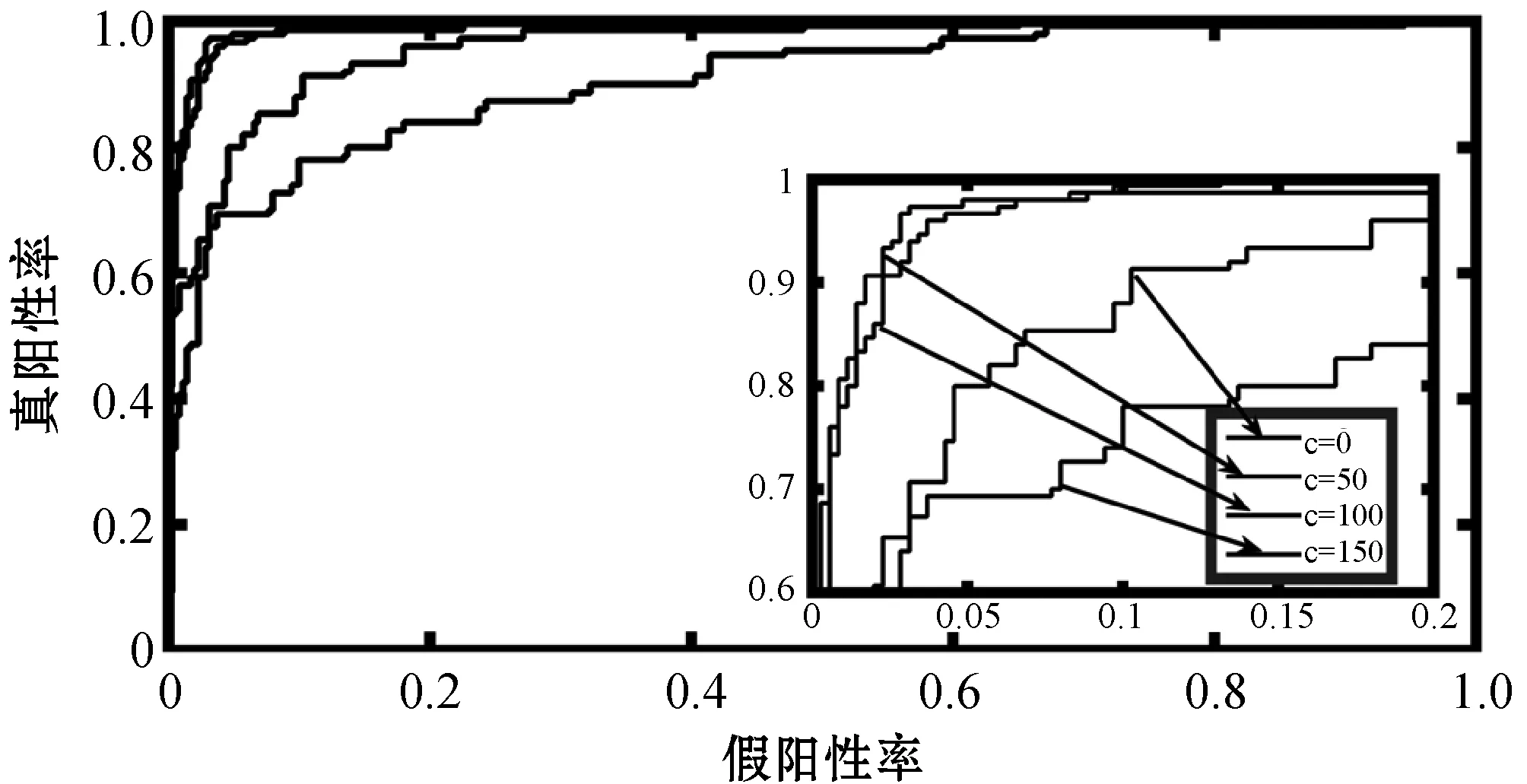
图1 不同参数c对应数据X中特征选择的ROC曲线

图2和图3反映了在最优参数λ1、λ2、c下,不同的参数a对样本数据Z的特征选择的准确性的影响。可以看出a=10和a=20时特征选择的准确度相差不大,a=0和a=1 000时模型的特征选择准确性明显低于a=10和a=20的准确度。a=0时Joint-CoReg模型对各类样本的典型向量无融合作用,此时模型相当于对各类样本分别协同回归，a=1 000时Joint-CoReg模型使得各样本的典型向量完全融合为一类，此时相当于将所有样本数据视为同类,图2和图3说明Joint-CoReg模型特征选择准确率高于CoReg模型特征选择准确率，Joint-CoReg模型具有选择类特征信息的能力。

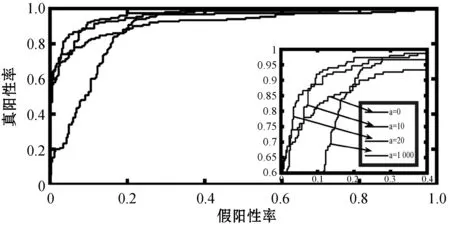
图2 不同参数a对应变量Z1特征选择的ROC曲线

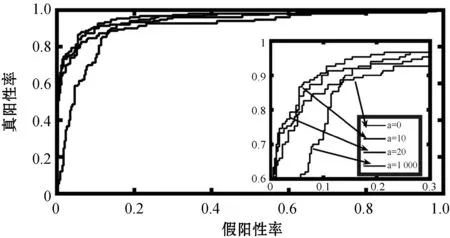
图3 不同参数a对应变量Z2特征选择的ROC曲线

3 结 语

本文建立了联合协同回归模型用于多模态高维数据的关联分析。 该模型在协同回归模型中加入Fused lasso惩罚来实现多类样本之间的联合作用, 实验结果中类相关特征的选择表明Fused lasso可以有效地实现多类样本的联合作用。模型求解部分对模型进行必要的简化，得到高效的迭代求解算法，该简化过程可保证模型的有效性，对于高维数据的模型求解具有重要参考意义。实验构造模拟数据，通过特征选择的准确率验证模型有效性，使用ROC曲线对比不同模型特征选择的准确率。实验结果表明，Joint-CoReg模型在保证变量相关性的同时实现了类相关特征选择，较CoReg模型有更高的特征选择准确率。模型建立过程中，在标签变量数据引入参数，并在实验部分讨论该参数变化对模型的影响，通过对比实验得出结论：对标签变量数据给定合适权重可提高模型性能。