基于预测校正的落角约束计算制导方法

刘子超，王江，何绍溟,*，李宇飞

1. 北京理工大学 宇航学院，北京 100081 2. 北京理工大学 无人机自主控制技术北京市重点实验室，北京 100081 3. 北京理工大学 信息与电子学院，北京 100081

随着现代防御技术的发展，装甲车辆、舰船、防御工事等目标的防御能力显著提升。当导弹以一定的角度命中这类目标时，能够得到更好的打击效果，因此一些制导律的设计中引入了落角约束。Ryoo等基于能量最优性能指标，选取剩余飞行时间的函数为性能指标的权函数，推导了最优落角约束制导律。张友安等应用Schwarz不等式求解了有无控制系统动力学情况下最优制导律的一般表达式。Erer等在比例导引律的基础上附加角度约束偏置项，通过偏置项缩小落角误差，实现落角控制。Liu等针对使用脉冲发动机控制的飞行器，提出了带角度约束的最优脉冲制导律。Park等选取剩余飞行距离的函数为性能指标的权函数，推导了带视场角约束的落角约束制导律。郭建国等将终端攻击角度约束转化为终端视线角约束，利用螺旋控制算法设计了一种二阶滑模变结构制导律。He等建立了时变加权视线角误差动力学，基于李雅普诺夫稳定性理论设计了滑模制导律。Kim等则在落角约束问题的基础上引入了视场角约束，提出了不依赖相对距离与视线角变化率的滑模制导律。在具有落角约束的制导律设计中，应用最多的是最优控制和滑模变结构控制思想。但是最优制导律对假设条件依赖性强，鲁棒性较差，滑模制导律又容易发生抖振，如何提高落角约束制导律的鲁棒性和稳定性仍然是飞行器制导系统设计的关键问题。

随着计算机技术的快速发展，几乎所有学科都走向定量化和精确化，从而产生了一系列计算性的学科分支。在飞行器制导控制领域，计算制导也获得了越来越多的关注。传统制导研究一般需要引入一些假设条件来推导解析制导律，例如常值速度假设，并且无法处理复杂的制导问题；而计算制导一般不依赖假设条件简化制导问题，而是使用数值计算方法生成制导指令，伪谱法制导以及深度学习制导都属于计算制导。

根据系统模型在计算制导中的应用，可以将计算制导算法分为两类：① 基于模型的计算制导算法；② 基于数据的计算制导算法。基于模型的计算制导采用参数化方法将连续空间的最优控制问题求解转化为非线性规划问题，通过数值计算求解规划问题获得最优解；基于数据的计算制导方法则是以深度学习为主要工具，从飞行数据中学习制导指令或系数与飞行状态之间的映射关系，根据飞行器的飞行状态动态调节制导指令，从而使飞行器状态收敛至期望的约束。

随着人工智能技术的发展，深度学习在制导控制领域的应用备受关注。深度学习计算量相对更少，能够提高计算制导的实时性，并且对非线性函数具有良好的拟合能力，因此近几年学者们对深度学习在制导控制领域的应用开展了大量研究。方科等使用深度监督学习根据当前飞行状态预估到达时间，然后根据时间误差对视线角走廊进行动态调整，该方法调整形式较为简单，但是没有考虑最优性指标。Shalumov使用深度强化学习设计了突防制导律，结合滑模制导的思想，学习制导律的切换策略。余跃和王宏伦使用深度监督学习处理传统预测校正制导算法的实时性问题，使用深度神经网络代替传统算法对导弹运动微分方程组的积分，提高了算法的实时性。Furfaro等使用深度强化学习训练制导律的系数，实现再入飞行器软着陆，但是整条弹道的奖励值需要在得到终端状态之后才能进行计算，存在稀疏奖励问题，初期收敛速度较慢，训练效率较低。

本文基于预测校正制导思想，结合监督学习和深度学习，提出了一种基于学习的计算制导方法(Learning-based Computational Guidance, LCG)。该方法首先训练深度监督学习预测落角，然后以偏置比例导引法为基础，使用深度强化学习输出偏置项，使预测落角向期望落角收敛。本文的主要贡献如下：① 提出了一种新的计算制导框架，该框架除了解决落角约束以外，能够推广应用于其它约束条件，如飞行时间约束，落速约束等；② 使用深度监督学习实时预测终端状态后引入深度强化学习模型中，解决了深度强化学习模型的稀疏奖励问题，提高了训练效率；③ 针对落角控制问题设计了考虑最优性指标的强化学习奖励函数，降低了能量消耗。

1 问题描述

针对二维平面下导弹攻击固定目标的落角约束问题建立弹目相对运动的数学模型，如图1所示。图中：为导弹飞行速度，为弹道倾角，、、分别表示升力、阻力、重力；为弹目视线角；为弹目相对距离；表示弹道轨迹。

图1 弹目相对运动模型Fig.1 Relative motion model of missile and target

导弹的运动学微分方程如下

(1)

式中：(,)表示导弹在平面中的位置；为导弹质量。各气动力为

(2)

式中：为升力系数；为阻力系数；为导弹的参考面积；为重力加速度；表示动压:

(3)

其中：为空气密度。

在导弹飞行过程中，攻角一般较小，气动系数可近似表示为

(4)

(5)

为了满足落角约束，导弹的终端位置与弹道倾角应当满足如下关系

=,=,=

(6)

式中：下标f表示终端状态；下标d表示期望状态。

虽然本文仿真模型以及方法设计基于二维纵向平面开展，但是本文提出的方法可以应用于三维场景。在三维场景中，滚转稳定导弹的制导问题可以分解至水平通道和垂直通道，解耦为两个独立的问题并分别进行分析。将本文的训练结果应用于二维纵向平面，然后将训练场景更换为水平通道，使用本文设计的算法训练适用于水平通道的模型，即可在三维场景的两个通道分别使用两个计算制导模型，实现三维场景制导。

2 带落角约束的计算制导框架

本文设计的LCG框架以偏置比例导引律为基础，偏置比例导引律一般具有如下形式

=+

(7)

式中：为比例导引制导律(Proportional Navigation Guidance, PNG)，负责缩小导弹的零控脱靶量(Zero Effort Miss, ZEM)；为偏置项，负责使预测落角收敛至期望落角。为了抵消重力的影响，中引入了重力补偿，表示为

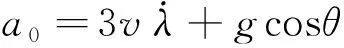
(8)

引入落角约束后，LCG框架如图2所示。该框架由两部分组成：深度监督学习预测模块(Deep Supervised Learning Module, DSLM)与深度强化学习校正模块(Deep Reinforcement Learning Module, DRLM)。在学习阶段，首先通过离线采集的标注数据训练DSLM，令DSLM学习飞行状态与落角之间的映射关系；当DSLM训练完成后，即可实时预测落角误差，令DRLM通过仿真飞行实验与导弹试错交互，使用交互生成的数据训练DRLM，改进偏置项的生成策略。当DRLM训练完成后，即可结合DSLM预测的落角误差实时动态地调节偏置项，使落角误差收敛。

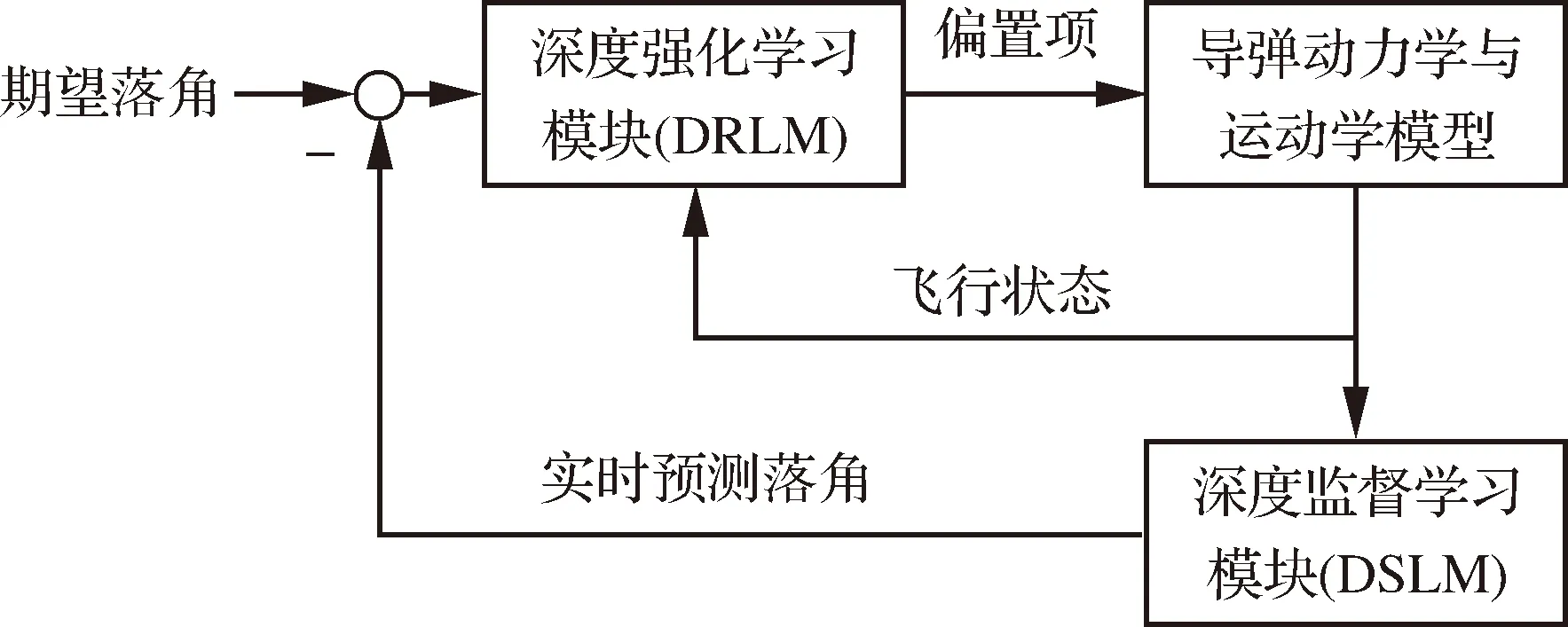
图2 带落角约束的计算制导框架Fig.2 Framework of learning-based computational guidance with impact angle constraint

在传统的预测校正制导中，预测模块使用弹道积分，根据导弹的当前状态预测终端状态，然后校正模块根据预测值与期望值的偏差调整控制指令，使偏差逐渐收敛。本文所提出的算法基于预测校正思想设计，其中DSLM根据飞行过程中实时变化的状态在每个周期预测终端落角，计算落角误差；DRLM根据落角误差生成制导指令并执行后，DSLM再基于新的状态预测落角。

训练DSLM使用的离线标注数据按照如下方式采集。首先令式(7)中的=0，制导律即退化为PNG。如果目标静止或机动形式已知，不考虑环境带来的扰动，一组发射状态生成的弹道具有唯一性，弹道上任意一点的飞行状态已知时，这条弹道对应的落角即可唯一确定；如果目标机动形式未知，随着导弹剩余飞行时间缩短，目标的机动范围逐渐缩小，落角预测误差随之收敛；由于DSLM使用飞行过程中的状态预测落角，不存在误差累积问题，当环境存在偏差或模型不准确时，落角预测误差也会随着导弹剩余飞行时间的缩短而收敛。在DSLM的训练数据采集阶段，以PNG为制导律，引入气动系数摄动，通过蒙特卡洛实验获取大量弹道数据，然后将飞行状态标注为输入数据，将终端状态标注为输出数据。

DRLM将制导模块视为智能体，将智能体以外的其它部件统一视为环境。智能体以导弹的飞行状态为输入，以偏置项为输出，以获得最大的总环境奖励值为目标，在与环境的试错交互中不断改进制导策略；环境奖励根据预测误差及其它约束项计算得出。相比传统方法，DRLM不需要求解制导指令与约束项之间的解析关系，因此不依赖假设条件来简化模型，也可以将一些过程约束引入制导律设计中。

与其它计算制导算法相比，基于预测校正制导思想的计算制导方法能够更好的适应训练模型偏差。这是因为预测校正制导对初始误差不敏感，同时校正模块中实时生成的校正指令也能对模型偏差引起的预测角落误差进行校正。因此本文设计的LCG框架具有较好的抗扰性、鲁棒性和自适应能力。

3 深度监督学习预测模块

传统的预测校正制导中，预测模块对运动学方程进行大量的数值积分，实际应用时存在实时性问题。深度监督学习的计算速度更快，输入当前状态即可实时预测落角，能够显著提高算法的实时性。

3.1 DSLM结构设计

DSLM使用具有多个隐层的神经网络，基于标注数据通过一定的训练方法拟合输入数据与输出数据之间的映射关系。典型的多隐层神经网络由输入层、输出层、以及多个隐层构成，每个隐层中包含了大量的神经元。DSLM使用的神经网络的结构如图3所示。

假设第层具有个神经元，+1层具有个神经元，则每个层的神经元执行的计算如式(9) 所示:

=()∈{1,2,…,}

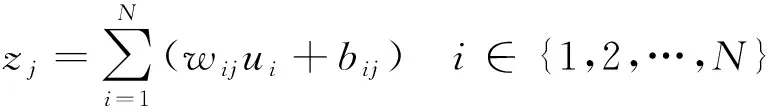
(9)

图3 DSLM的网络结构Fig.3 Network structure of DSLM

式中：为单个神经元的输入；为单个神经元的输出；为中间变量；为神经元的权重；为神经元的偏移量；{,,…,}构成了第+1层的输入；{,,…,}为第+1层的输出；下标表示数据来源于第层的第个神经元，下标表示数据在第+1层的第个神经元中计算；(·)是激活函数。

当前神经网络的输出层设计为落角，输入层设计为飞行状态向量(,,,,,)。其中：和表示导弹在平面中的绝对位置，与、一同表征导弹自身的当前飞行状态；、表示当前弹目相对状态。在飞行过程中，这些飞行状态一般可通过弹载传感器或导引头获得。

本文设计的神经网络使用3个全连接层作为隐层，每层有100个神经元。使用线性整流单元(Rectified Linear Unit, ReLU)作为输入层和隐层的激活函数，输出层不设置激活函数。ReLU的形式为

(10)

3.2 DSLM学习过程

DSLM的训练一般需要大量的标注数据样本。以PNG为制导律，对式(1)进行数值积分，通过蒙特卡洛仿真生成足够多的弹道数据，在仿真过程中引入气动系数随机摄动，使训练样本覆盖更大范围的样本空间。在本文设定的场景中，使用PNG攻击固定目标时不会发生脱靶现象。当导弹满足≤时，即为完成一次仿真飞行实验，为最大脱靶量。

第次仿真飞行实验完成时，弹道对应的落角随即获得，以弹道上的所有飞行状态向量为输入，对应的输出标注为，作为一系列标注数据样本。

(11)

当样本采集完成后，将样本中2%的数据划分为测试集，2%的数据划分为验证集，剩余96%的数据作为训练集。令=[,]，定义损失函数为网络参数的函数

(12)

(13)

式中：为学习率，在训练前人为设定初值，训练过程中，ADAM优化器会自适应地动态调节学习率。

4 深度强化学习校正模块

本文设计的DRLM使用近端策略优化算法(Proximal Policy Optimization, PPO)。PPO具有两个神经网络，分别为策略网络和评价网络。策略网络表示当前状态与指令之间的映射关系；评价网络估算当前状态的潜在价值，然后结合已实施的指令获得的奖励值序列，计算这些指令的奖励相对于潜在价值的优势函数。当优势函数为正，则增大已实施指令在策略中的概率；当优势函数为负，则减小这些指令的概率。为了减小训练过程的波动，更新策略时还需要确保新旧策略之间的差异较小。

4.1 落角约束问题的强化学习模型

在强化学习模型中，智能体以试错的方式进行学习，与环境交互后获得奖励，以最大化总环境奖励值为目标，学习当前状态下的最优控制指令。强化学习过程可用时间序列={,,,…}表示，={,,}。其中：为环境在时刻的状态；为智能体在时刻所采取的行为；为在时刻环境给出的奖励。在下一时刻，智能体将作用于环境，环境随即给出奖励+1，并从状态变为+1。在应用强化学习算法前，首先需要针对落角约束问题定义智能体与环境交互的接口，即状态、行为、奖励。

将DRLM的行为定义为式(7)中的偏置项。在试错训练初期可能会产生过大的偏置项，致使导弹脱靶，因此需要对偏置项进行限幅为

=||≤

(14)

式中：为偏置项的限幅。

策略网络以为输入，为输出。为了设计状态，首先分析与存在相关关系的变量。弹道可以表示为导弹运动方程组的积分，积分时间即为导弹的剩余飞行时间。当导弹与目标之间距离较远时，积分时间较长，导弹能够以较小的实现落角控制；当缩短，导弹需要使用更大的才能纠正同等的落角误差。因此，与存在负相关关系；预测误差与显然是正相关的，越大，需要的也越大。因此将状态设计为

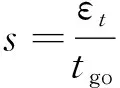
(15)

对奖励的设计是最重要的，因为合理能够确保学习过程收敛，并且能够提高学习效率。除了落角约束，导弹还需满足一些额外的约束来满足最优性指标。不同约束可能具有不同的非线性形式，首先使用指数函数将不同约束的尺度统一，然后赋予不同的权重来调节各约束的对智能体的影响。奖励的形式为

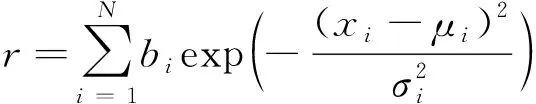
(16)

式中：为权重系数；为约束项；为偏移系数；为缩放系数；下标表示第项约束。其中满足

(17)

训练好的DSLM给出了预测落角，结合期望落角即可计算预测的落角误差。文献[25]提出了预测校正制导中误差动力学的最优收敛形式。最优误差动力学定义为

(18)

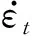
(19)

式中：,0表示误差的初值。当=0时，=0。误差动力学式(18)能够最小化一些性能指标，为了模拟最优误差动力学，针对落角约束的奖励项设计为式(20)的形式。

(20)

其中：为落角约束的缩放系数。

根据能量守恒定律，在飞行期间执行机动消耗的能量越少，击中目标时的动能越大，攻击效果越好，因此需要对机动的能量消耗进行约束。在最优控制中，能量消耗的目标函数一般设计为

(21)

计算状态的潜在价值时隐含了对奖励的积分，因此可以将该约束项设计为

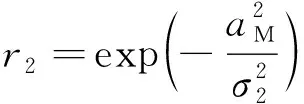
(22)

式中：为能量消耗约束的缩放系数。

结合式(20)和式(22)，引入各约束项的权重，奖励值即为

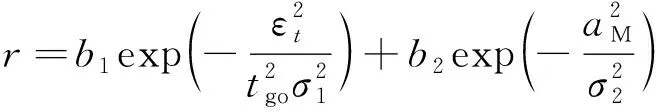
(23)

将落角约束问题抽象为强化学习问题后，行为、状态、奖励如式(14)、式(15)和式(23)所示。为了加强终端落角与脱靶量在训练过程中的影响，在仿真飞行实验完成时，调节最后一个周期的奖励值

(24)

式中:为脱靶量；为终端落角误差。

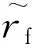
4.2 近端策略优化算法

PPO是一种基于策略的深度强化学习算法。策略可定义为智能体在不同状态下的各种行为的概率分布，用(|)表示。PPO将行为视为随机变量，该随机变量服从一定的概率分布，概率分布的参数由PPO中的策略网络输出，行为从这一概率分布中随机选取。PPO的网络结构如图4所示。

图4 PPO的网络结构Fig.4 Network structure of PPO

1) 评价网络

PPO的目标是寻找一个策略，使智能体在未知环境中获得最大的总环境奖励值，但是总环境奖励值一般无法直接计算。在离散系统中，总环境奖励值具有如下形式

(25)

为了表示不同状态下的总环境奖励，用数学期望的形式定义的状态值函数()，表示状态的潜在价值:

(26)

为了评估行为的优劣，一些强化学习算法定义了在状态下行为的行为值函数(,)，表示行为的潜在价值:

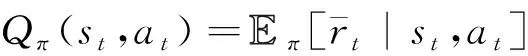
(27)

()可用(,)表示为

(28)

(29)

(,)=(,)-()

(30)

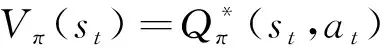
(31)

式中：为评价网络的参数。

参数更新如式(32)所示:

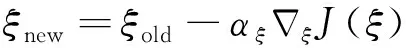
(32)

式中：为评价网络的学习率。

但是优势函数中的两个值函数仍然是无法直接计算的，使用多步估计法估算优势函数，表示为

(33)

式中：为估算步长，与交互样本量相关。

2) 策略网络

策略网络以状态为输入，以策略的参数为输出。一般使用高斯分布作为策略的概率分布，策略网络的输出即为高斯分布的均值和标准差。PPO是基于置信域策略优化算法(Trust Region Policy Optimization, TRPO)改进设计的，在TRPO中，策略网络的目标函数为

(34)

(35)

根据式(30)，优势函数(,)表示当前行为值函数相对于当前状态值函数的优势，若优势函数为正，则应当提高当前行为在策略中的概率；反之，若优势函数为负，则需要降低当前行为在策略中的概率。TRPO通过最大化目标函数实现了这一过程，并且使用限制了策略更新幅度的上界，提升了策略更新过程的稳定性。但是KL散度的计算量仍然较大，而且TRPO在更新策略时还使用了共轭梯度法等方法，工程实现较为不便。

PPO简化了TRPO的计算，使用剪切函数约束策略的更新幅度。PPO的目标函数为

() =

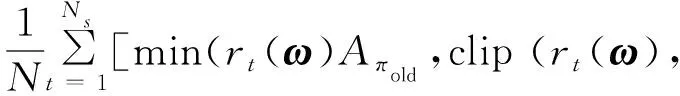
(36)

式中：()表示比率函数，

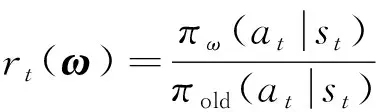
(37)

clip((),ϑ)表示剪切函数，为

clip ((),ϑ)=

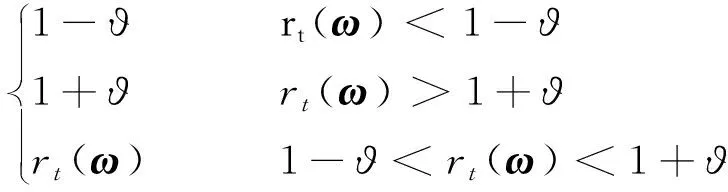
(38)

式中：ϑ为约束策略更新幅度的剪切参数。

由式(38)可见，剪切函数将新旧策略的比率约束在(1-ϑ,1+ϑ)内，随即约束了新策略的更新幅度。策略网络参数的更新公式为

(39)

式中：为策略网络的学习率。

4.3 网络结构与学习过程

本文使用的PPO中，策略网络和评价网络均均由4个全连接层组成，使用了2个隐层，各层维度如表1所示。除了输出层，其它各层均使用ReLU作为激活函数。策略网络的输出层使用两种不同的激活函数，均值输出使用的激活函数tanh为

(40)

tanh函数能够将网络的输出限幅至[-1,1]。将输出层的输出乘以式(14)中的，即可将策略网络输出的均值限制在[-,]之间。

标准差输出使用的激活函数为softplus，形如式(41)。Softplus函数的输出恒大于0，满足标准差的物理意义。

()=ln(1+e)

(41)

本节的强化学习与3.2节的监督学习获取样本的方式有一定区别。监督学习的样本采集是非交互的，可以在采集完成后开始学习，而强化学习的样本是交互式的，需要在学习的同时生成新的样本，边采样边学习。在学习过程中，PPO设计了一个长度为的缓冲区，智能体与环境使用旧策略交互次，将交互过程生成的交互时间序列={,,,…，}存储于缓冲区中。更新策略网络时，首先使用式(33)估算(,)，然后根据高斯分布的概率密度函数计算中已执行行为的(|)。策略网络生成新的策略后计算(|)，然后代入式(36)计算目标函数，使用ADAM优化器求得目标函数对的梯度并更新策略网络，使目标函数最大化。

表1 策略网络与评价网络各层维度Table 1 Layer size of actor network and critic network

更新评价网络时，目标函数中的优势函数(,)在更新策略网络阶段已经获得，可直接代入式(31)。使用ADAM优化器优化评价网络的损失函数，更新评价网络的参数，使损失函数最小化。两个网络更新完成后，清空缓冲区，然后使用学习后的新策略交互次，重复这一学习过程，直至导弹落地或击中目标。

5 仿真实验

为了测试LCG的性能，本节给出了三维空间的数值仿真实验。首先建立了三维空间的导弹运动模型，然后使用DSLM分别学习了水平通道与垂直通道的飞行状态与落角之间的关系，使用DRLM实现了两个通道的落角控制，最后使用蒙特卡洛仿真验证了LCG的有效性。

5.1 三维空间导弹运动模型

三维空间的导弹运动微分方程为

(42)

式中：为飞行速度；为弹道倾角；为弹道偏角；、、为导弹在空间中的位置；为导弹质量；表示升力；表示侧向力；表示阻力；表示重力。各气动力形式为

(43)

式中：为升力系数；为侧向力系数；为阻力系数；为动压；为参考面积。攻角和侧滑角一般较小，气动系数可近似表示为

(44)

(45)

攻角、侧滑角与制导指令之间M、M的关系如下

(46)

5.2 DSLM仿真实验

在训练DSLM之前，需要设计仿真飞行实验，以PNG为制导律采集弹道样本。本文设计的DSLM可以在水平通道和垂直通道独立训练，然后分别部署于两个通道，因此分别了开展纵向平面和和侧向平面的仿真实验，并且训练了两个通道DSLM模块。

导弹的初始飞行状态以均匀分布的方式从一定范围内随机选取。各初始飞行状态的取值范围如表2所示，表3给出了导弹关于马赫数的气动系数，由于本文使用轴对称弹体模型，导弹水平通道的气动参数与垂直通道的气动参数相等。导弹的参考面积=0057 m，质量=200 kg，重力加速度=981 m/s。攻角与侧滑角均限制于区间[-20°,20°]内。其中纵向平面重复了两组蒙特卡洛实验，第1组实验不考虑气动系数摄动，通过1 000次仿真实验获得9 191 009组样本；第2组实验设定摄动参数，在每次实验的初始化阶段随机缩放气动系数，的取值范围为(0.8,1.2)，运行1 000次仿真实验共获得10 207 724组样本，首先使用无气动系数摄动的样本训练DSLM，训练结束后使用有气动系数摄动的样本继续训练DSLM；侧向平面运行了一组蒙特卡洛实验，使用摄动参数随机缩放气动参数，的取值范围为(0.8,1.2), 运行1 000次仿真实验共获得21 339 882组样本，使用该样本训练另一个DSLM，用于水平通道的落角预测。

表2 导弹初始飞行状态Table 2 Initial flight conditions of missile

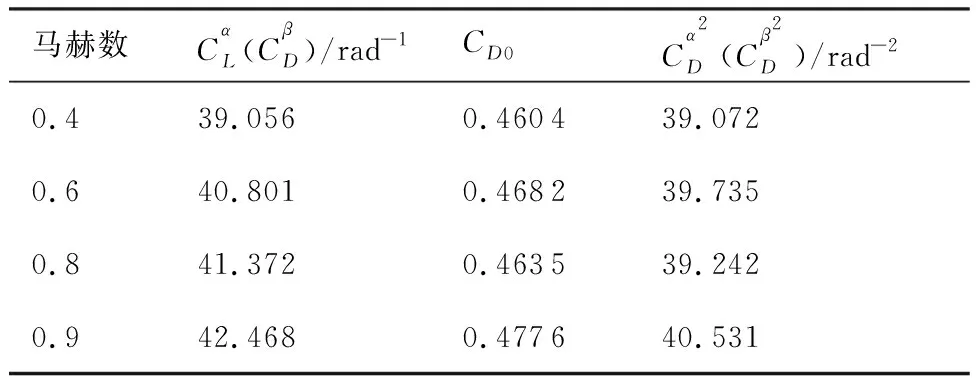
表3 气动系数及导数Table 3 Aerodynamic coefficients and derivatives

使用测试样本测试训练好的两个DSLM，测试结果如图5所示，测试集的预测误差统计特征如表4所示。由图5可见DSLM对落角具有良好的预测效果，预测值与实际值几乎完全重合，由表4可见预测误差的均方根误差较小，最大值虽然较大，但较大的误差一般出现在弹道初段，预测误差随着导弹接近目标逐渐收敛。实验结果证明了DSLM的输入输出选取合理，学习效果良好。

图5 DSLM测试结果Fig.5 Test results of proposed DSLM predictor

表4 DSLM预测误差的统计特征Table 4 Statistical characteristics of DSLM prediction error

5.3 DRLM仿真实验

1) DRLM的学习过程

由于DRLM的输出仅依赖落角预测误差，而水平通道和垂直通道的气动系数相近，可以使用相同的DRLM模型，因此仅在二维纵向平面训练DRLM，然后将训练好的DRLM部署于两个通道。DRLM的样本获取方式与DSLM不同，采用了边采样边学习的方式。根据4.1节设计的强化学习模型在导弹仿真飞行实验中部署PPO算法，按照表2中给出的取值范围随机选取导弹的初始飞行状态，在学习阶段期望落角从[-30°,-150°]中随机选取。PPO学习时使用的超参数如表5所示。式(15)和式(20)中的可以通过式(47)近似计算得出:

(47)

运行仿真程序500次，记录每一次仿真飞行实试验奖励值，然后除以该次飞行时间，记为单次仿真飞行实验的奖励。使用滑窗平均计算多次飞行实验的平均奖励，奖励随学习过程收敛的曲线如图6所示。从图中可见，经历了100个周期的波动后，奖励值开始单调上升，并在第200次试验后趋于稳定。

2) DRLM性能分析

设定一系列的场景对训练后的LCG进行仿真测试，导弹以=200 m/s，=0°，=0°，=-20 km，=10 km，=5 km的初始状态发射，期望弹道倾角和期望弹道偏角(,)分别设定为(-20°,20°)，(-40°,0°)，(-60°,-20°)，各飞行试验对应的弹道曲线、制导指令、飞行速度、速度方向角如图7所示。

表5 DRLM的超参数Table 5 Hyper parameter setting in training DRLM

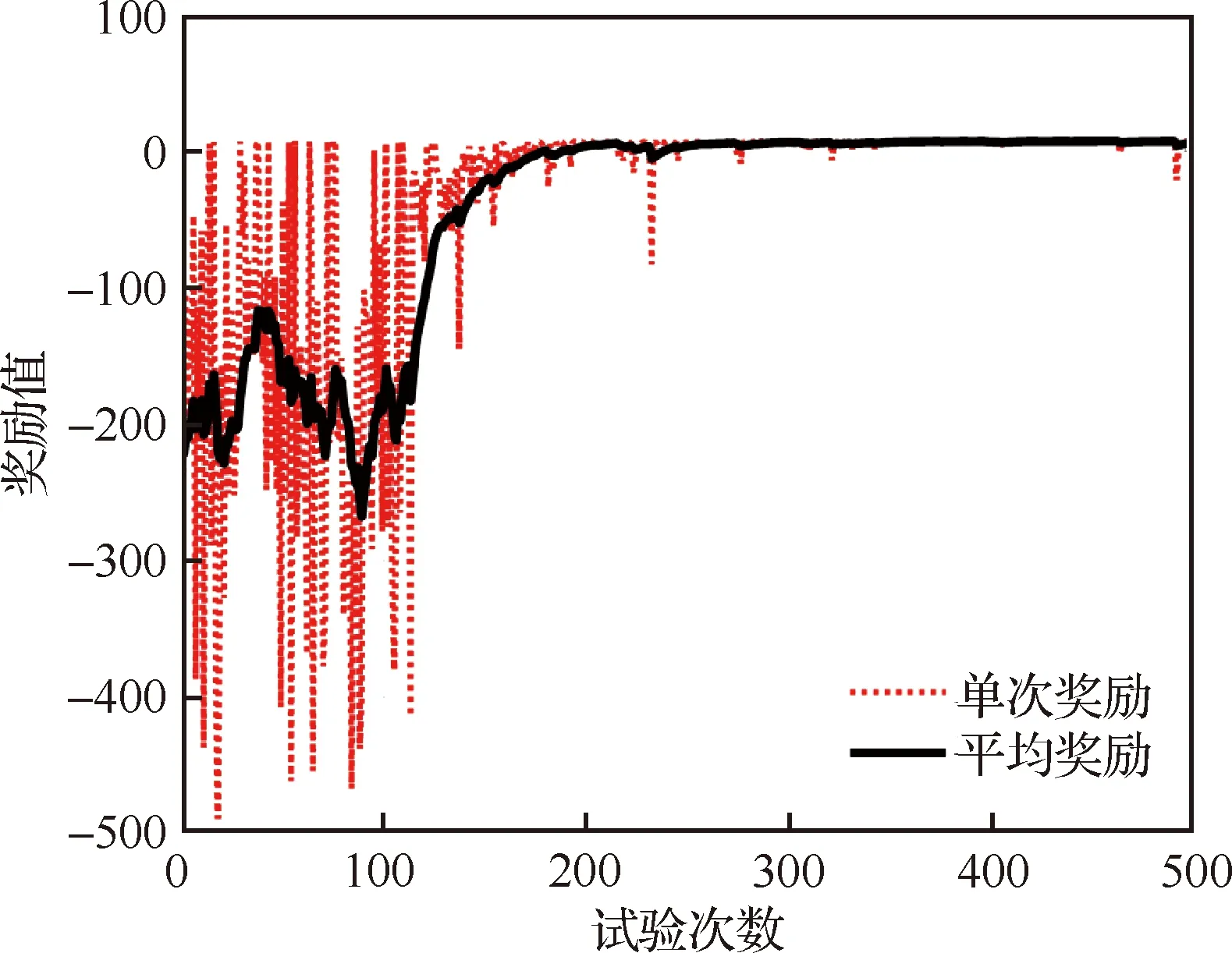
图6 DRLM学习过程奖励曲线Fig.6 Learning curves of the DRLM

从图7中可见，导弹以期望的落角命中目标，制导指令有界。阻力与重力的联合作用致使飞行速度变化，当-sin>时，飞行速度增大；反之，当-sin<时，飞行速度减小。导弹的和在仿真终端时刻为(-19.79°,19.86°)，(-40.09°, -0.39°)，(-59.92°,-19.99°)，验证了LCG能够以较高的精度实现三维落角约束。

图7 LCG制导性能曲线Fig.7 Performance curves of LCG

实际场景中一般存在模型偏差与环境扰动，导致气动系数摄动。为了验证LCG的鲁棒性，在期望落角[,]为[-20°,20°]时，分别将表3的气动系数放大1.2倍、缩小0.8倍，实验结果如图8所示。从图8可见，在不同的气动系数下导弹的飞行轨迹基本重合，并且均以期望的落角到达目标位置，且在到达目标时，落角误差收敛至0附近。导弹的和在仿真终止时刻分别为(-19.28°,19.79°)，(-19.79°, 19.86°)，(-19.94°,19.91°)，验证了基于预测校正制导思想设计的LCG能够适应气动系数摄动，具有较强的鲁棒性。

图8 不同气动系数下的LCG制导性能曲线Fig.8 Performance curves of LCG with different aerodynamic coefficients

3) LCG与弹道成型的对比分析

广义最优弹道成型制导律(Trajectory Shaping Guidance, TSG)是一种带落角约束的最优制导律，其推导过程引入了常值速度假设，没有考虑气动力的影响，在上述假设条件下TSG满足能量最优的性能指标。三维场景中TSG的公式为

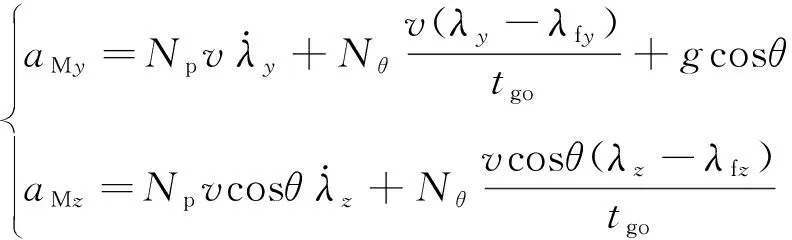
(48)

式中：、为导航系数；f、f为终端弹目视线角；对固定目标有f=f、f=f。各导航系数形式为

(49)

式中：为可调参数，≥0。

取与2)相同的初始发射条件，设期望落角(,)为(-40°,0°)，分别设定=0,1,2，运行仿真实验对比3组不同参数的TSG与LCG的制导效果，实验结果如图9所示。两种制导律均使导弹以期望的落角到达目标位置，虽然在=0时TSG为能量最优的落角约束制导律，但是TSG的推导过程没有考虑气动力的影响，使用了常值速度假设，在实际环境中无法满足能量最优。而LCG在训练阶段考虑了气动力的影响，DRLM通过试错交互学习得到了满足落角约束的制导策略，并且能量消耗优于TSG，说明本文的DRLM的奖励设计合理，在实际环境中LCG的制导性能优于TSG。

图9 LCG与TSG性能对比Fig.9 Performance comparison of LCG with TSG

5.4 蒙特卡洛实验

为了测试LCG在不同状况下的制导性能，使用蒙特卡洛仿真实验，发射条件从表2给出的范围中随机选取，期望落角(,)分别从(-60°,-20°)、(20°,20°)中随机选取。分别以LCG与=0的TSG为制导律重复100次蒙特卡洛实验，统计LCG与TSG的落角误差，统计特征与箱线图如表6、表7和图10所示，图中、分别表示垂直通道和水平通道的落角误差。从箱线图可知，LCG落角误差的方差、异常值均小于TSG，验证了该方法对环境变化不敏感，具有较强的抗扰性、鲁棒性；LCG脱靶量的上限、上四分位数、中位数均小于TSG，验证了LCG能够按照要求完成制导任务，制导性能优于TSG。

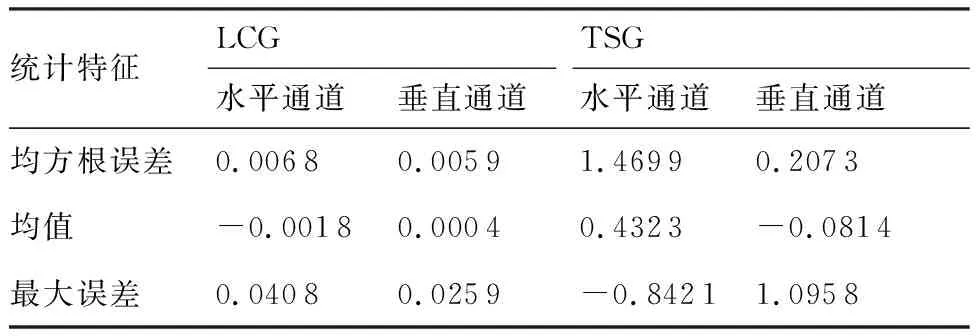
表6 落角误差的统计特征Table 6 Statistical characteristics of impact angle error

表7 脱靶量的统计特征Table 7 Statistical characteristics of miss distance

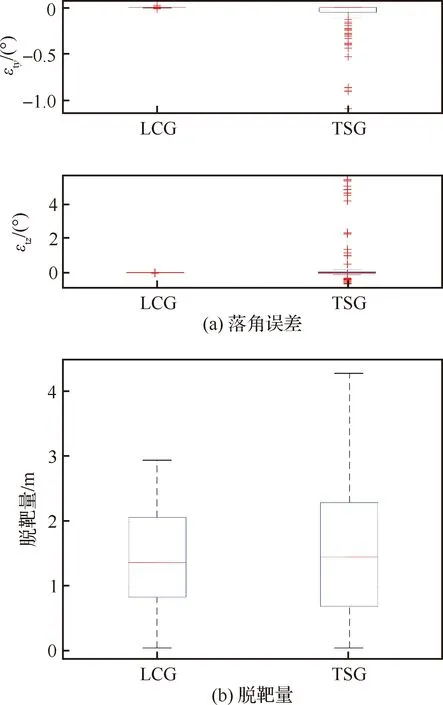
图10 蒙特卡洛仿真实验结果对比箱线图Fig.10 Box plot of Monte Carlo experiment

5.5 计算性能实验

与传统的制导律相比，计算制导方法需要消耗更多的计算资源。为了验证本文提出的LCG在嵌入式系统的工程实用性，依次使用TensorFlow 1.13.1、X-CUBE-AI 6.0.0、STM32CubeMX 6.2.1分别将LCG中的预测网络、策略网络部署于STM32F405测试平台，其中X-CUBE-AI是ST公司开发的AI工具箱，可以优化神经网络在STM32上的运算速度。分别部署DSLM的预测网络和DRLM中的策略网络，实验流程如图11所示。

图11 STM32F405实验流程示意图Fig.11 Experimental flow diagram of STM32F405

PC通过串口下发数据，使两组神经网络各运行10次，然后通过串口采集神经网络的输出值，并统计神经网络运行耗时。将STM32F405的输出值与PC平台的神经网络输出值进行对比，测试X-CUBE-AI优化神经网络造成的精度损失，并计算平均耗时，结果如表8所示。

表8 STM32F405运算精度与耗时Table 8 Precision and time consumption of STM32F405

从表8可见，两组网络在STM32F405单次运行的平均耗时分别为1.145 ms和0.272 ms，计算精度高，实时性好，说明LCG具备工程实用价值。

6 结 论

1) 提出了一种基于预测校正的落角约束计算制导方法，该方法由深度监督学习模块与深度强化学习模块组成，深度监督学习模块在飞行过程中实时预测落角，深度强化学习模块对落角误差进行校正。引入深度监督学习网络解决了传统强化学习方法中的稀疏奖励问题。

2) 设计了计算制导方法中的各输入输出变量，经训练后实现了落角约束制导，并以仿真实验的形式测试了计算制导的性能，该算法训练过程的收敛速度较快，训练后的制导效果较好，能量消耗与控制误差均小于弹道成型制导律。然而，由于该类算法较依赖训练时所使用仿真模型的准确度，当训练模型存在较大偏差时，将影响本文所提出方法的制导性能，后续将开展基于数据的计算制导方法的鲁棒性研究，探索弱监督学习、迁移学习在当前计算制导框架的应用。

3) 经STM32F405测试，该框架计算精度与效率高，实时性好，具有良好的工程应用价值。该框架对预测校正制导思想的使用除落角约束以外，也可以应用于其它不同约束，如飞行时间约束、末速约束等。