自由航线规划技术与算法研究
2022-09-06刘芊池皮晚晴杨坤奇寇云凯
刘芊池 皮晚晴 杨坤奇 寇云凯 周 航
中国民航大学中欧航空工程师学院 天津 300300
1 概述
自由航线空域(Free Route Airspace,FRA)是指在一定的空域内,航空器可以自由地选择飞行路线,允许飞机选择其最直接的(或最优的)飞行航线,而不是按照规定的飞机航线飞行。航空器可实时根据飞行环境改变航线,达到减少飞行时间与航空公司运营成本,降低航空器燃油消耗,减少污染物排放的目的。自由航线空域的概念是美国联邦空管局在1994年为了提升空域容量并解决航线拥堵的问题提出的构想[1]。此外,自由航线空域也是欧洲单一天空计划的重要组成部分[2]。因此,实施FRA计划的地区可同时优化整片空域的航路航线,在出现极端天气情况或军航活动时,动态地优化航线网络能充分利用空域资源,有效避免限制区域,是增强民航运输科学性、经济型、安全性的有效手段。国内民航业起步较晚,自由航线及其优化的相关项目并未实施。未来,我国将成为世界第一航空运输大国[3]。因此,可预见自由航线在我国实施,以提高空域利用率,适应民航业的发展要求。
目前,针对自由航线优化问题的相关研究一直非常活跃,形成了新的研究热点。2001年,Jardin等[4]首先提出基于最近邻算法的特定风速下水平飞行的航空器航线优化。后来又出现了两类优化方法:一类是包括建立离散网络的航线优化方法,例如,A-star算法[5]和Dijkstra算法[6],这类方法一般被认为是解决路径优化问题(Path Optimization Problem,POP)的最优方法;另一类方法类似于Farin[7]发明的前传播法,例如,水平设置法、快速行进法、有序逆风法等。
文中使用了一种涟漪扩散算法(Ripple-Spreading Algorithm,RSA)[8]来解决自由航线空域中的航线优化问题。在动态空域模型中,变化的气流速度、移动的恶劣天气区域、禁飞区等将作为影响因素。RSA算法对于动态环境的路线优化十分有效,通过单次运算即可以获得最佳路线。本文将介绍基于涟漪扩散算法的动态空域下的自由航线优化模型与算法,并通过模拟测试验证方法的有效性。
本文结构如下所述,第二部分针对单机高空巡航飞行的问题,建立自由航线优化问题的数学模型;第三部分应用动态加权路网中的涟漪扩散算法;第四部分通过仿真实验说明该方法的有效性;第五部分为本文总结。
2 数学模型
2.1 问题描述
本项研究是研究优化飞机自由航路的模型和方法。在这里只研究飞机从给定的出发位置到目的地位置的巡航过程。首先,假定飞机以一个恒定的真空速(true airspeed,TAS)在一个固定的飞行高度(FL)巡航,此时飞机的地速为:
其中(x,y)是飞机的位置坐标,va是真空速,θa是飞机的航向,vw是风速,θw是风向,他们的关系如图1所示。
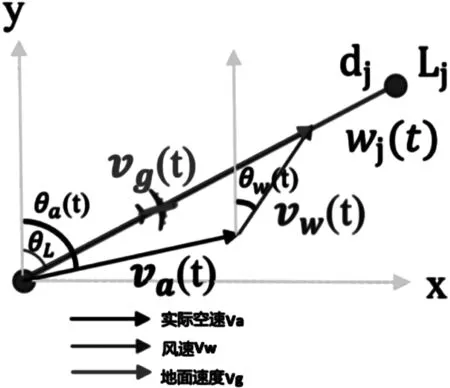
图1 地速、真空速和风速的矢量
目的是找到最优路径,也就是使飞机飞行时间最短的路径。因为飞机飞行的真空速TAS是常数,所以这条路线也代表着飞机所消耗的燃料最少。在考虑随时间变化的恶劣天气地区后,飞机飞行的优化路线可以描述为一个最小化问题。
其中t1代表飞机的起飞时间,tr代表飞机到达目的地的时间,(xi,yi)代表起飞位置,(xf,yf)代表飞机的目的地位置,Rp(t)因不利因素需要绕行的地区,共有Nr个。
2.2 自由航线
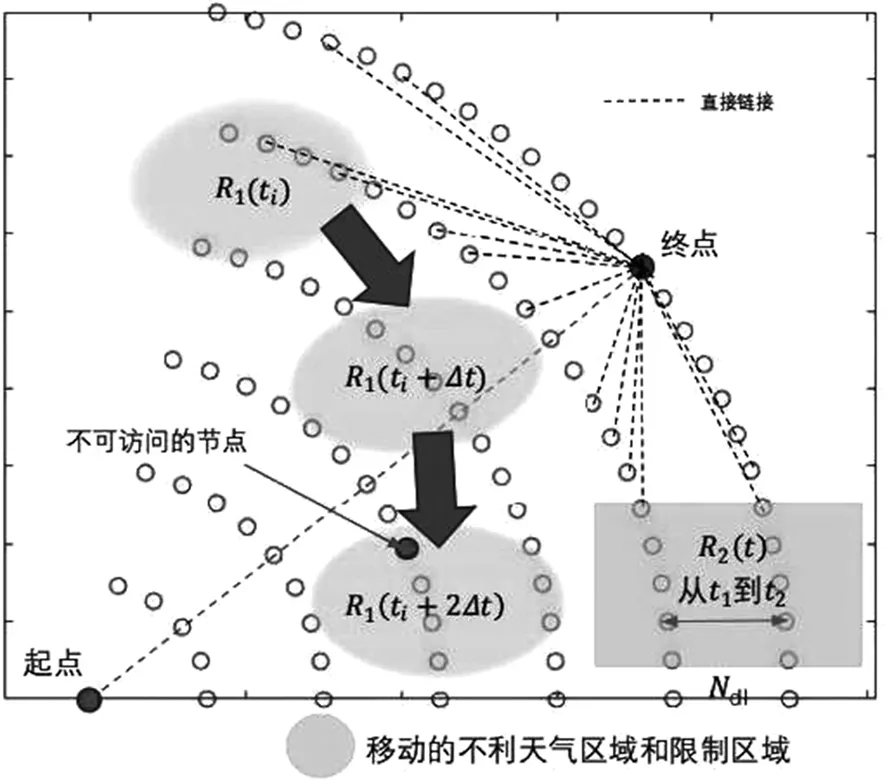
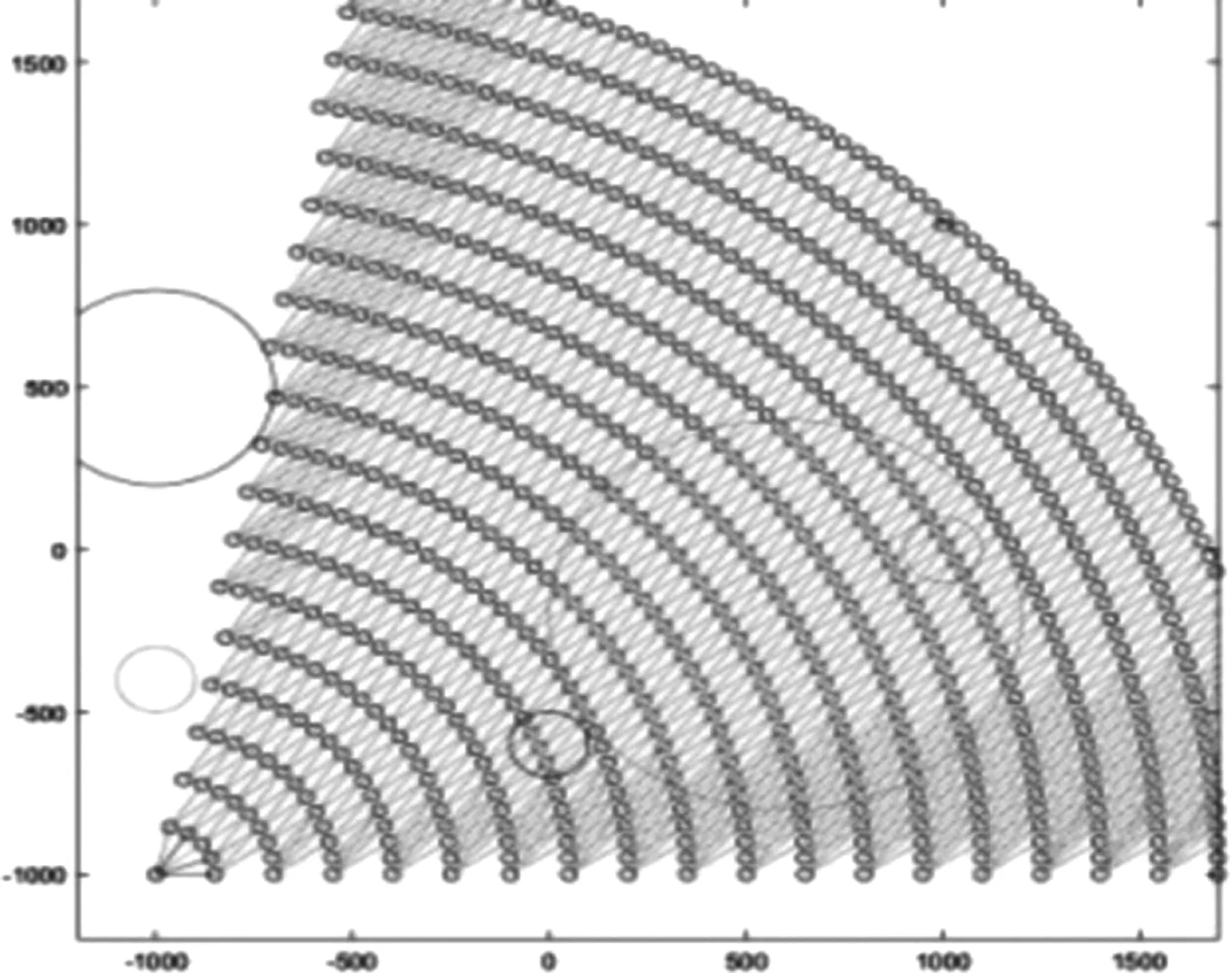
为模拟自由航路问题,本文建立了一个基本的路网模型G(V,L),其中主要包含两个参量,分别是节点集合V和链接集合L,节点集合可表示为V={Vi}i∈[1,Nnode],包含Nnode个节点,而这些节点之间的连接集合L可表示为L={Lj}j∈[1,Nlink]。首先,rmax和θd分别表示飞机起飞位置(xi,yi)到目的地位置(xf,yf)的距离和方向角,选择一个角度θ∈[θd-θmax,θd+θmax]且半径r∈[0,rmax]的扇形作为节点网络区域,如图2(a)所示。其次,在半径范围为r∈{kΔr,rmax}(k∈[1,int(rmax/Δr)])的圆形区域,每个节点具有固定的间距Δl,如图2(a)所示。
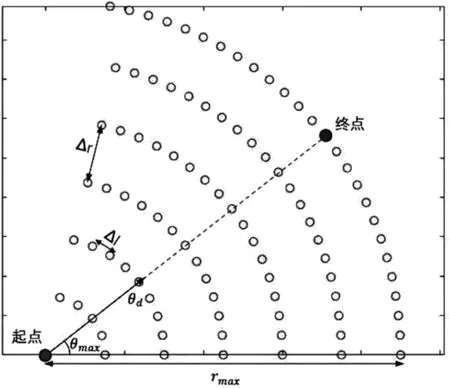
(a)
(b)
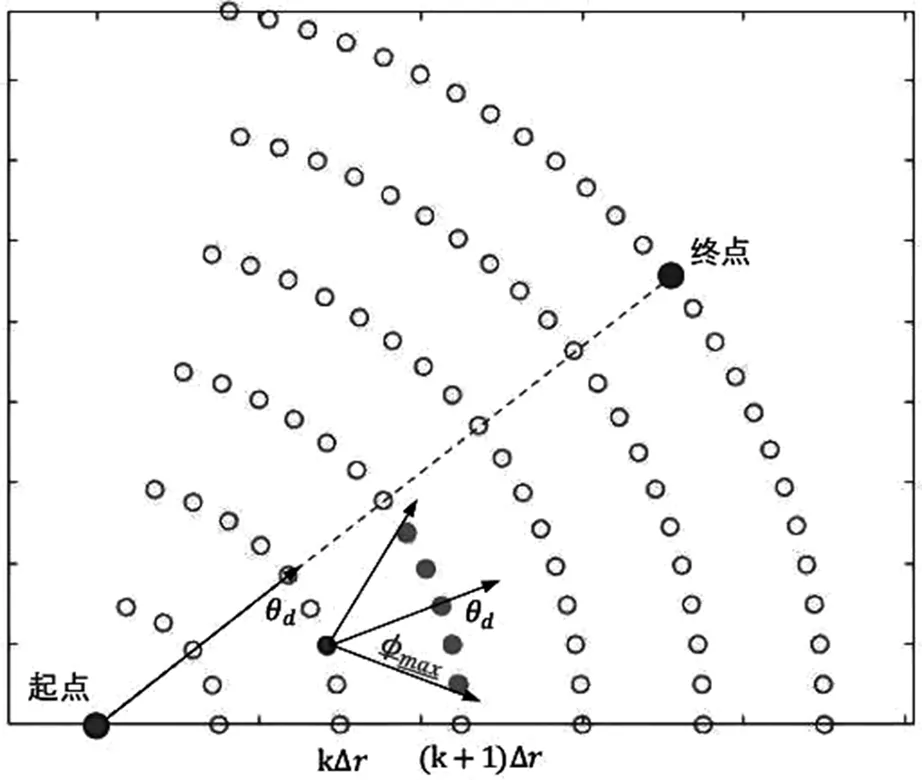
(d)图2
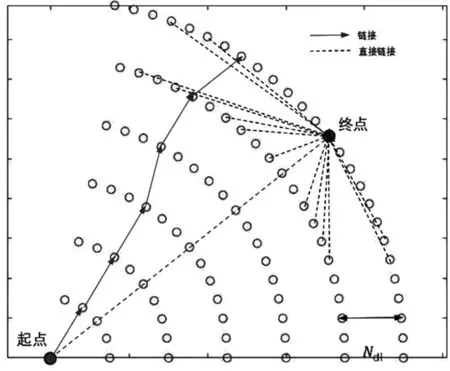
模型中节点间的链接L对应飞机可能自由飞行的路线,对于每个节点来说,它只连接到下一个圆形上的节点,因此可以得到方位角θ∈[θd-φmax,θd+φmax],φmax表示飞机航向角度的最大范围。此外,为了避免出现飞机无法有效到达目的地的情况,增加了最后的圆Ndl和代表目的地的节点的直接链接,如图2(c)中的虚线所示。每个链接的权重为wj,其中j∈[1,Nlink],代表飞机通过长度dj的链接Lj的飞行时间。
2.3 动态空域模型
在动态空域中,需要考虑气流的速度和方向、移动的不利天气区域和限制区域。
首先,在图2(d)中给出了依赖于时间的气流的速度和方向。采用了从美国航空气象中心测试数据服务器的API接口获取的真实气流数据。因此,采用了一个四维的(时间加上三维坐标空间)线性插值空间,风的矢量表示为(vw(t),θw(t))(x,y,z)。
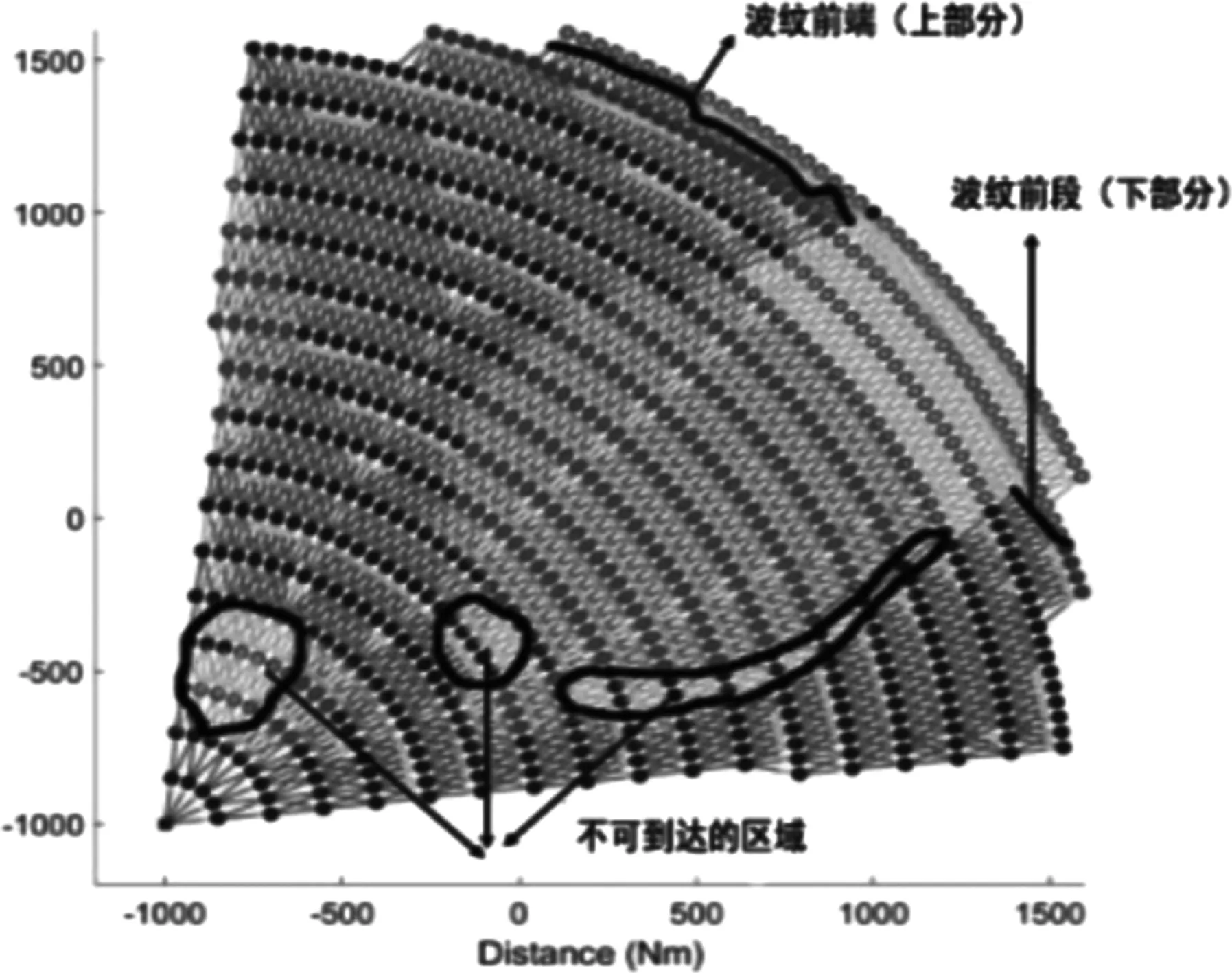
其次,恶劣天气可能会对飞机造成严重危害,应该避免在这些区域飞行。在飞机飞行期间,不利天气区域可能会持续移动,如图2(d)中的椭圆形区域所示。在进行优化的过程中,Rp(t),p∈[1,Nr]这些节点是不可访问的。
最后,考虑了危险区域、限制区域和一些禁区的影响。如图2(d)中的矩形表示,该区域在t1到t2需要绕行。限制区域也可以用Rp(t)表示,且不随时间变化。
3 运用涟漪扩散算法优化自由航线
考虑到动态空域中气流的方向和速度、飞行禁区以及时刻变化的天气云团等因素,于是便在原有的航空路网的基础上对自由航路问题进行了优化。在这部分中,首先介绍涟漪扩散算法的基本原理,以及对此算法进行优化和改进,使其与动态路网更加契合。
3.1 涟漪扩散算法(RSA)的基本原理
通常情况下,为了能够很好地解决动态路径优化(DPO)问题,我们会采用对线路在线重新优化(OLRO)的方法。但OLRO这种方法并不是从起始点出发去寻找最佳路径,仅仅是在部分节点或者链接上改变当前行驶路径,这便导致了OLRO方法所得到的优化路径并不是最优解。
怎样才能避免这一情况出现?RSA将环境参数和路径优化过程共同演化,因此只需将这一算法运行一次便可得到最优路径。RSA算法过程如图3所示,图中位置实时变化的禁区内包含的节点和链接用红色标示,这一区域自西北方向往东南方向移动。在初始时刻ti,一个涟漪自起始点出发以恒定的速度向各个方向进行扩散,当涟漪到达了新的节点时将从这个节点产生新的涟漪向各个方向进行扩散,依次进行下去直到t=ti+mΔt(m∈N)时刻到达终点,最终通过反向跟踪涟漪找到一条最佳路径。同理,对于自由航路的优化,可以加入天气以及飞行禁区等因素,运用RSA算法找到最佳自由航路。
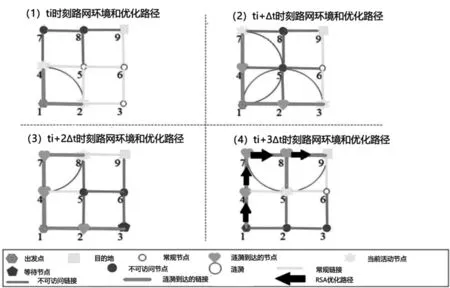
图3 在存在不可到达的区域时涟漪扩散算法的优化过程
3.2 具有动态网络权重的涟漪扩散算法
传统方法无法有效模拟自由航路优化问题中实时气流对飞行器的影响,因此本文提出了基于动态赋值路网改进的涟漪扩散算法。基于该算法模拟的自由航路路线,能够充分利用飞机巡航时的时变性气流,从而以更快速度到达目的地。
正如2.3动态空域模型中所提到的,可以用如下式表示的风向和风速,对空间和时间进行离散化,得到风向风速数:
(vw(t),θw(t))(x,y,z)
需要对每一次t=ti+mΔt时刻,重新依据风的参数重新赋值。例如,链接Lj的赋值ωj(t)可以通过图1所示计算,认为飞机沿连线Lj飞行,地面速度矢量用如下公式表示,vg(t)方向应该与链路相同:
vg(t)=va(t)+vw(t)
可得:
那么对于所有t=ti+mΔt(m∈N)时刻的权重{ωj(t)}j∈[1,Nlink],将依据实时风参数进行重新计算,从而便建立了一个动态网络权重的路网。
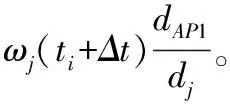
虽然涟漪的传播速度保持不变,但动态赋值网路导致飞机沿每个链路的飞行时间随时变气流参数的变化而变化。最后,通过在动态赋值网路运行一次RSA,便可得到在有气流存在情况下的最佳自由航路。
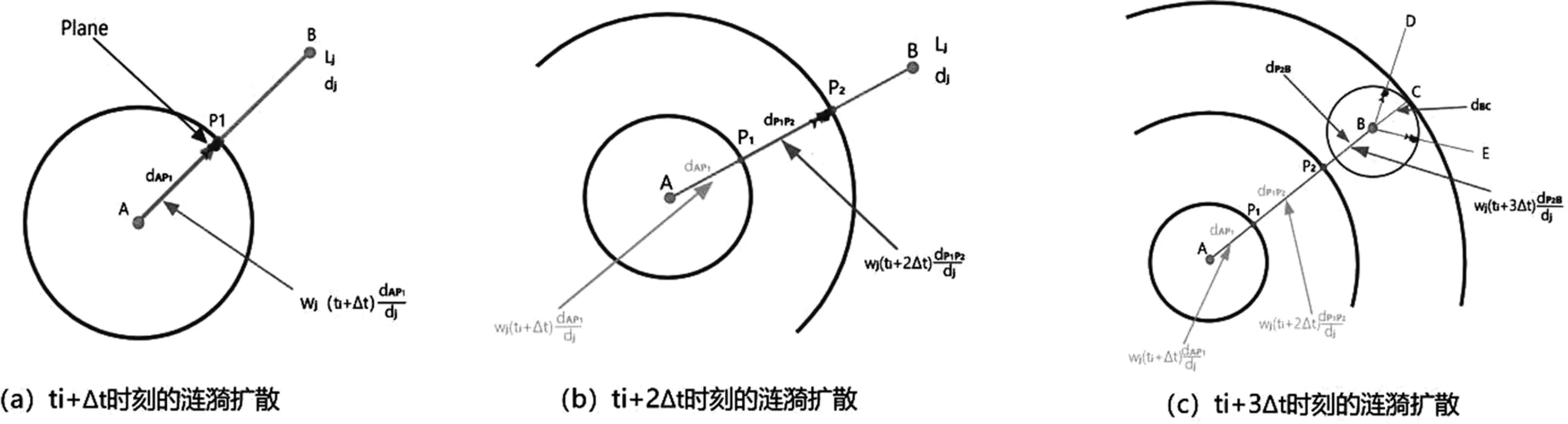
图4 在动态路由网络下涟漪扩散过程及每个部分的权重
4 应用优化方法进行仿真测试
在复杂空域中,对飞机的自由飞行路径的优化进行数值试验。测试是在MATLAB环境(R2018a)中进行的处理器Intel(R)Core(TM)i7-8550U CPU @ 1.80GHz RAM 8GB。
其中仿真权重包括,参与计算的取值区间x∈[-1200,1700],y∈[-1200,1700],单位为海里(Nm),起始位置为(xi,yi)=(-1000,-1000),目标位置为(xf,yf)=(1000,1000)。我们选择飞机的运行速度为va=500N/m,这是民用航空飞机常见的巡航速度。
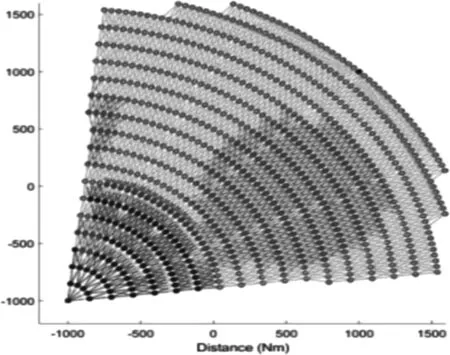
网络图的权重包括Δr=150Nm,Δl=50Nm,θmax=40°,Фmax=35°,Ndl=2。这些权重的意义和第二部分中的相同,运行出的路线网络图如图5所示。
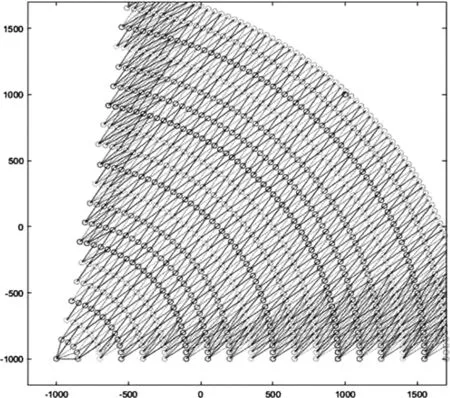
图5 对路由网络的情况进行数值实验
我们设置几个恶劣天气区域和限制区域,如下表所示,我们假设所有的区域都是圆形,前三个区域对应移动恶劣天气区和它的相应速度,后两个区域是固定限制区域。

恶劣天气区域及限制区域初始位置半径移动速度1(-1000,-400)100(75,-45)2(-1000,500)300(12.5,25)3(600,-200)600(-37.5,65.5)4(0,-600)100(0,0)5(1000,0)100(0,0)
气流数据是通过对预测数据[位置(x,y,z)和时间t]进行四维差值得到的。图6绘制了不同时间的风向量的计算域。我们设置涟漪扩散的速度是50/△t,也就是说,在△t的时间内,涟漪的半径增加50Nm。
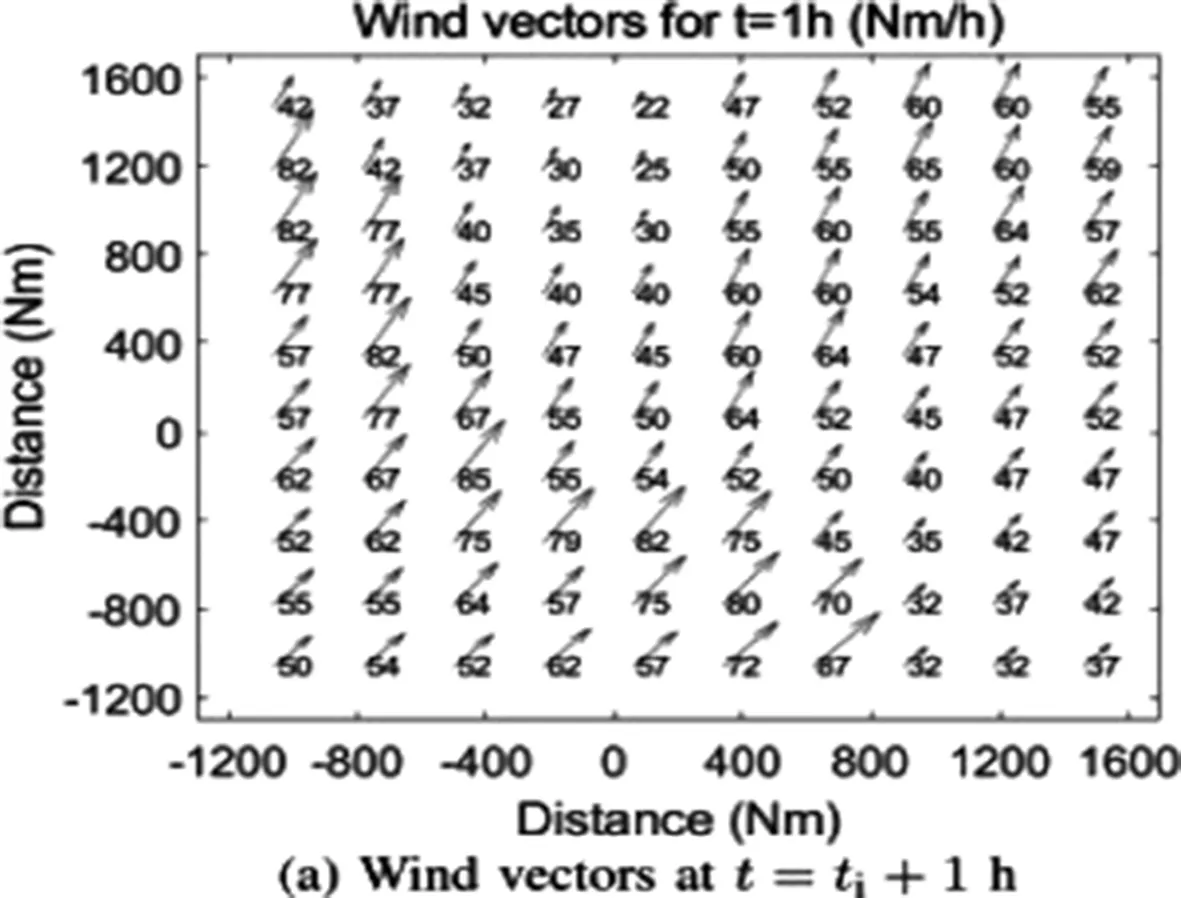
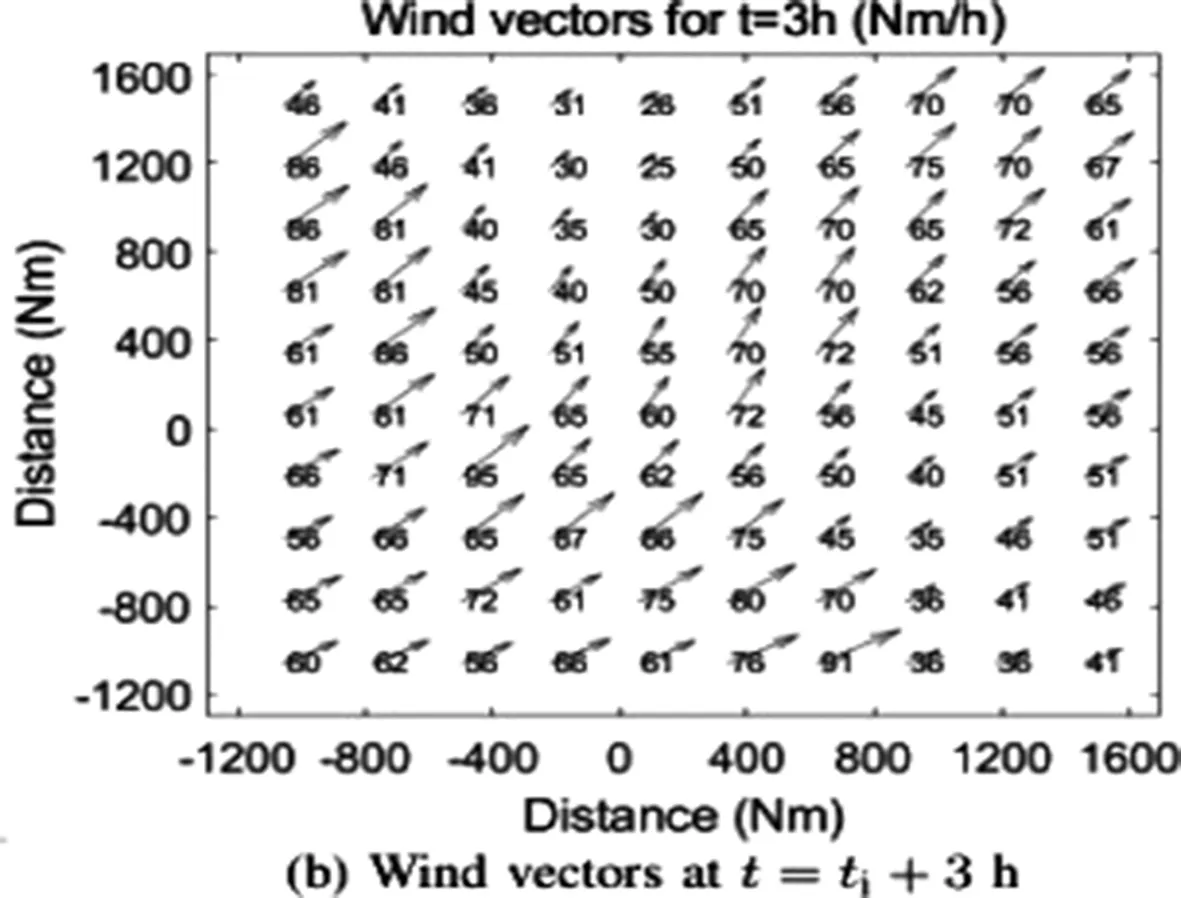
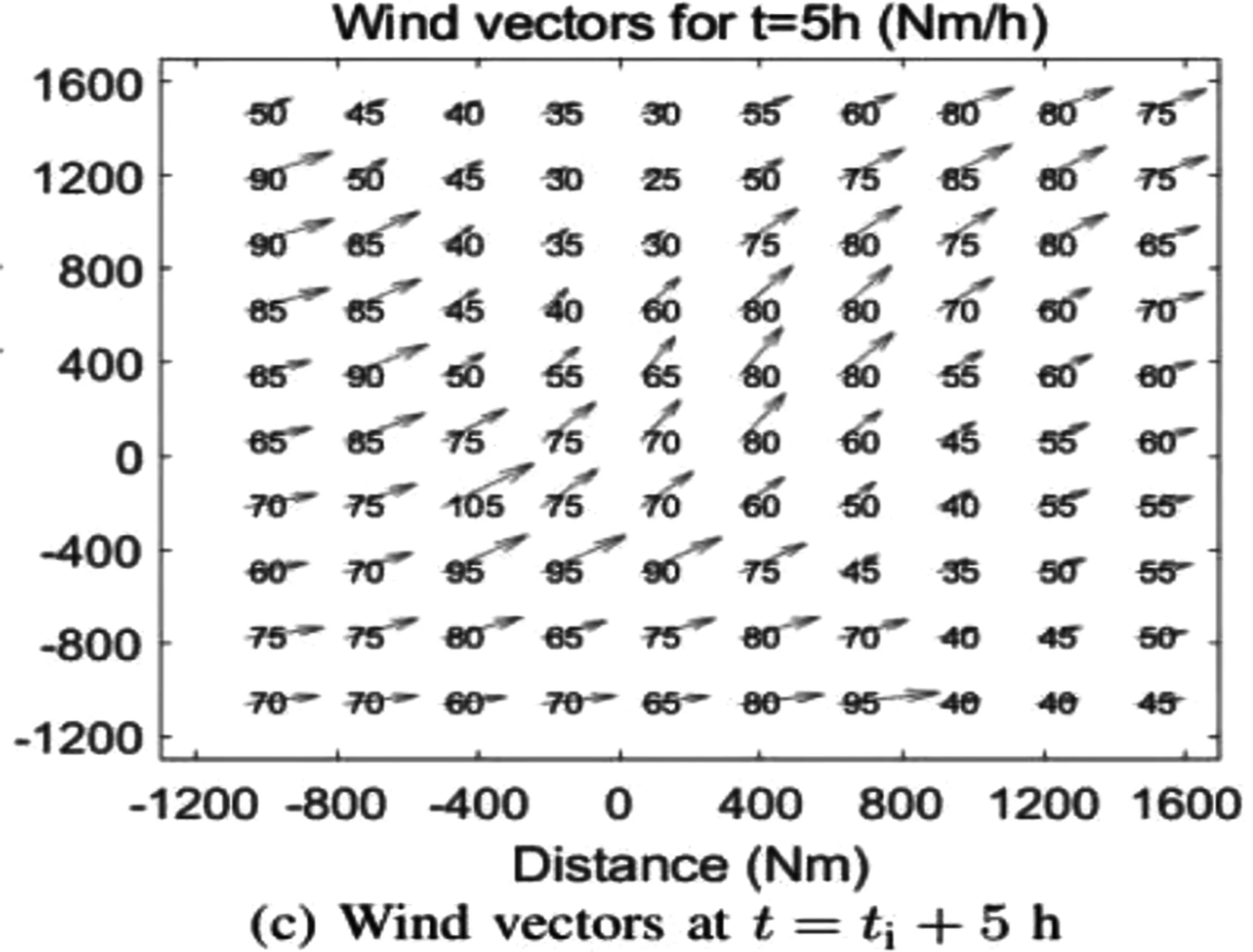
图6 在不同时刻风的参数
在第三部分介绍的RSA应用于基于动态网络权重的飞行路线优化。在执行一次运算后,即可得到一条最优路径。优化的中间过程如图7所示。圆内的区域代表恶劣天气和限制区域,实心圆代表已经运行的节点。在图7(d)中,被粗线圈起的区域是无法到达的节点和路线。除此之外,我们还可以看到上部分的涟漪传播前沿要比下部分的离目的地更近。
(a)在t=tih (b)在t=ti+1.6h
(c)在t=ti+3.4h (d)在t=ti+5.0h
本次动态空域的最优飞行路线如图8(a)所示。最优路线长度总和是2926.2Nm,飞行时间是5.18h,程序运行时间为67.9s。在该路线中,飞机利用气流的优势在最短的时间里避免危险区域,到达目的地。我们将这个结果与不考虑气流因素的结果相比较,如图8(b)所示,这两种飞行轨迹受气流影响并不是相同的。在不考虑气流的测试中,优化路径总路程为2908.4Nm,飞行时间是5.92h。即使它的飞行路程更短,但相较于前者,它的飞行时间增长了0.74h。此次程序的运行时间为2.5s,由于本次测试不考虑动态空域,所以运行时间要比前者短很多,结果符合预期。因此,文中的方法在解决动态空域中飞行路径计划的问题中具有有效性。
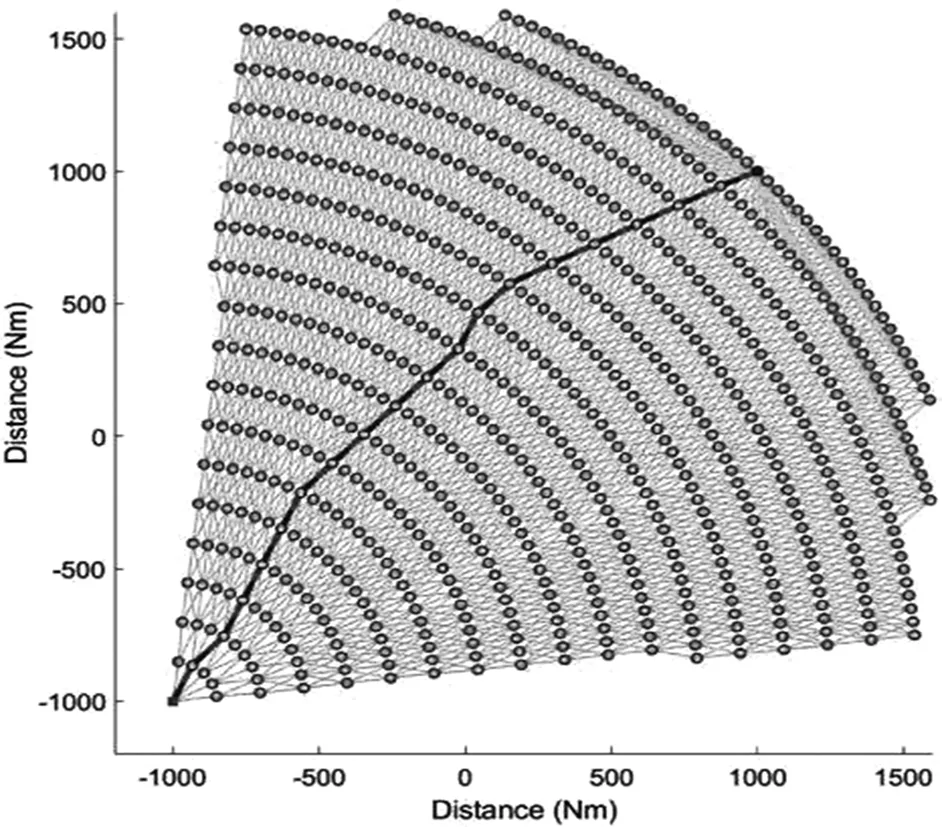
(a)存在在气流
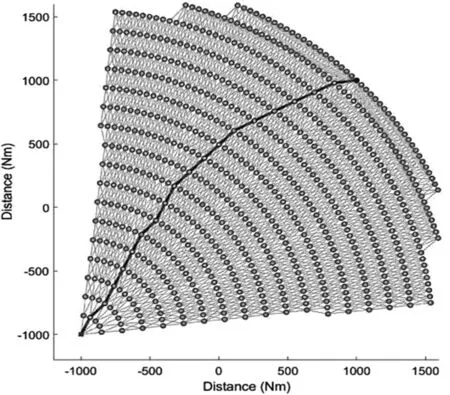
(b)不存在气流图8 自由航路在两种情况下的优化结果
结语
本文对自由空域下单机航线的优化问题进行了建模,将恶劣天气、禁飞区、气流作为影响因素。这种方法的主要优点是将复杂环境下的航线优化简化为数学模型,通过应用RSA算法解决问题并且可以通过模拟仿真实验验证。
通过进一步地研究,我们可以考虑以下几方面问题:该方法可以应用于实际的航线优化问题,还可以应用于文章中相对复杂的网络,也可以将该方法进一步应用于多机的航线优化问题。
