BP 神经网络在玉米干燥含水率预测中的研究

雷得超，付彦涛，金厚熙，李东洋，杨雨彤，句 金，任守华

（黑龙江八一农垦大学信息与电气工程学院，黑龙江 大庆 163319）

中国是粮食生产大国，2020 年玉米产量为26066.5 万t。如果玉米收获后，未达到安全存储水分要求，就会造成玉米发芽或者霉变等严重损失，这对粮食安全存储形成挑战[1]。 为保证粮食品质安全，需要将收获后的玉米烘干使其含水量达到合格的存储标准[2]。本研究从干燥理论上阐述适用于玉米干燥的数学模型，由于玉米干燥过程中复杂的非线性关系，本文构建了玉米干燥BP 神经网络预测模型， 由于排粮电机转速能够影响玉米在烘干塔的时间， 该模型把排粮电机转速作为模型输出， 通过排粮电机转速预测值与真实值作对比进行仿真预测。 仿真结果表明，该预测模型能够有效预测排粮电机转速，控制玉米在干燥塔内烘干时间预测出机玉米含水率。

1 玉米干燥机理分析

1.1 薄层干燥模型研究

薄层干燥数学模型是指烘干物料厚度在2cm以下， 通过烘干热风进行干燥， 它描述了在一定风量、 风温相对湿度条件下谷物含水率随时间的变化关系[3]。 薄层干燥模型由美国学者W V Hukill 提出，该模型假设为粮食干燥过程中温度不变， 粮食干燥速度（dm/dt）与粮食含水率高于平衡含水率差值成比例。 如公式1 所示：

为方便计算采用水分比表示干燥过程， 如公式如2 所示：

在薄层粮食干燥中使用最广泛是Page 模型[4]，该模型在玉米干燥中使用广泛， 有关学者研究出玉米干燥常数与玉米烘干影响因素的关系。 Page 模式如公式3、公式4 所示：

式中：x= 0.01579-0.01413Rh+0.0001746Ta， y=0.6545+0.07867Rh+0.002425Ta

式中k 为干燥常数，1/h；MR 为粮食水分比，%；M 为T 小时后含水率，%；Me 为干基平衡含水率，%；Mo 为干基初始含水率，%；A 为干燥常数1；t为干燥时间，h；Ta 为热风温度，℃，Rh 为空气相对湿度，%。

1.2 设备仪器

本实验数据采集地为黑龙江省大庆市大同区和平牧场，该农场每年收购湿粮为4.2 万t，降水率为13%~16%。 农场干燥塔为连续式横流粮食干燥塔，长宽均为5 m，高度为25.6 m，每天烘干玉米为300 t。该干燥塔包含玉米输送机、初清筛、玉米湿粮提升机、烘干塔、热风炉、热风机、冷风机及排粮装置。 烘干塔物理模型如图1 所示：

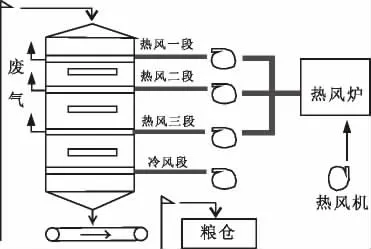
图1 烘干塔物理模型图

1.3 烘干过程分析

玉米经过送粮装置，进入烘干塔内部烘干，烘干塔内包含粮食预热段、恒速干燥段、降速干燥段、缓苏段以及冷却段，最终通过排粮输送装置送到仓库。在这个过程中， 干燥塔为烘干过程提供了闭环的工作环境，因此送粮装置、输粮装置以及排粮电机转速之间的合理配置尤为重要。 因此排粮电机转速直接关系到玉米在各个干燥区间的烘干或通过时间，最终影响出机玉米含水率。

2 BP 神经网络预测模型搭建

2.1 网络模型结构确定

BP 神经网络是一个多输入单输出的非线性信息处理节点群，每一个节点是一个神经元，这些节点组成的网络就是神经网络[5]。 BP 神经网络包含输入层，隐含层，输出层[6]，神经网络的构建不单要确定好输入层、输出层，隐含层神经元个数也极其重要。隐含层须满足公式5、公式6 要求：

式中m 为隐含层神经元数量，x 为输入层神经元数量，y 为输出层神经元数量，R（10）表示1~10 之间的随机整数。本研究将玉米初始入机含水率、烘干热风温度和玉米入机温度作为输入量， 排粮电机转速作为输出量，因此本研究中x=3，y=1，m=3~12。

2.2 神经网络模型建立

由2.1 分析可知， 该网络模型结构为3-J-1，即3 个输入节点，1 个输出节点，BP 神经网络结构如图2 所示：

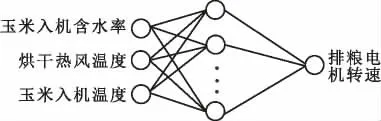
图2 BP 神经网络结构图

BP 神经网络激活函数包含线性函数，正切函数以及Sigmoid 激活函数，研究表明[7]，Sigmoid 激活函数能够增强神经网络非线性映射能力， 本研究采用Sigmoid 激活函数。

在数据选择与处理方面， 本研究采用和平农场玉米烘干过程中测定的100 组数据，其中80 组作为训练数据，20 组作为预测数据， 数据归一化选择matlab 自带的mapminmax 归一化函数。

2.3 神经网络参数确定

在训练之前需要确定好学习参数， 为避免学习率过高造成局部最小值以及太低造成学习时间过长，学习率一般设置在0.01~0.1 较为合适，本研究中设置学习率为0.01。 训练目标最小误差设置为0.001，使模型拥有较高的学习精度。 如果神经网络学习超过多少次仍不能收敛则结束训练， 本研究中设置训练次数为10 000 次。

2.4 模型仿真结果分析

用测定的数据进行训练BP 神经网络， 使得对非线性系统拥有预测能力。本研究程序在调试中，以此对3~13 作为隐含层个数， 发现当隐含层神经元个数为5 时，训练效果最佳。 为防止过拟合，Matlab把数据分成3 份，分别为训练、验证、测试，最后为总体拟合， 训练数据参加训练， 其它用于评估模型性能， 相关系数R 越接近于1，则拟合效果越好，通过训练输出拟合线可以看出相关系数R 为0.98419，回归直线方程为Output=0.96*Target+0.007，该模型能够对预测值和实际值有效拟合， 该模型验证系数为0.954 27，测试系数为0.911 18，总体相关系数为0.971 99，输出拟合线如下图3 中a~d 所示：

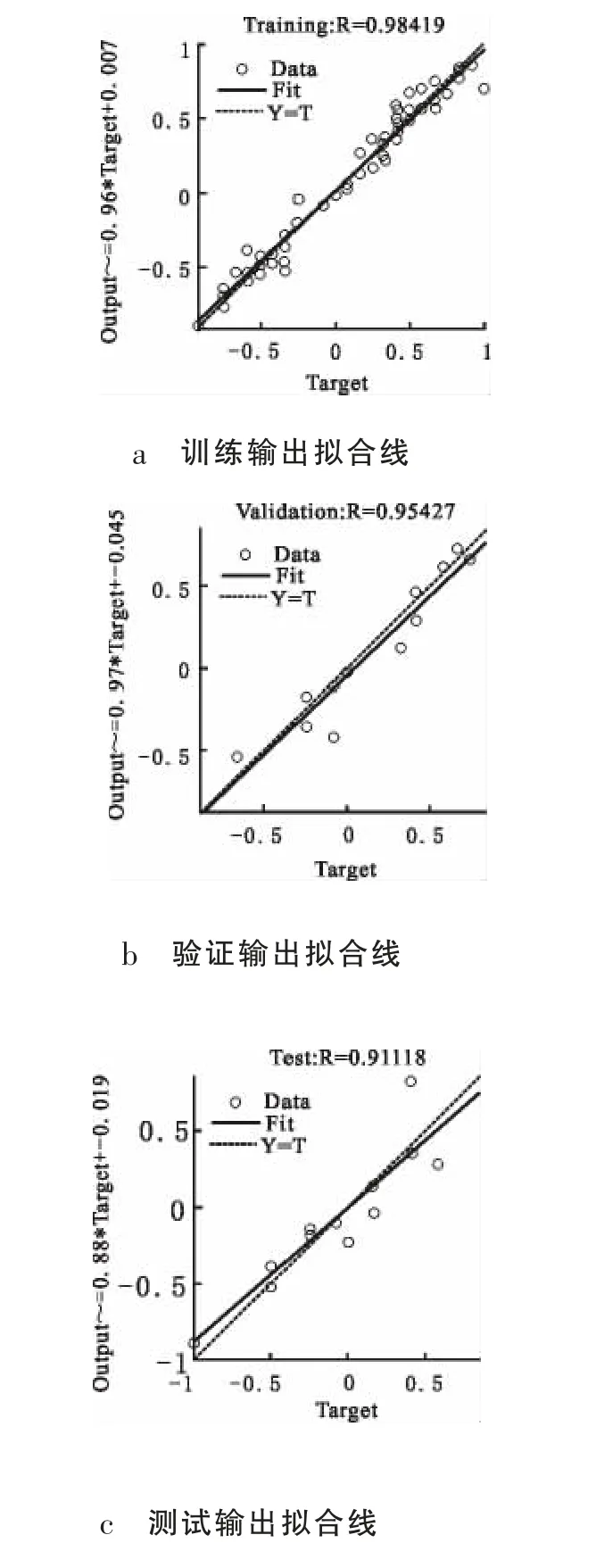
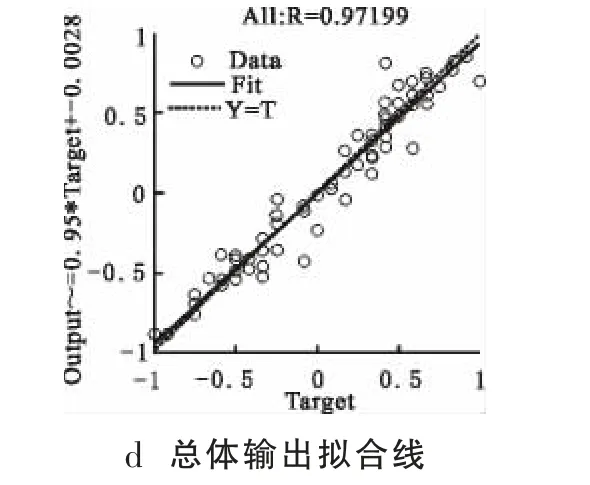
图3 输出拟合路线图

该模型使用均方误差验证模型性能， 如图4 可知训练误差在0.01。训练进行时，目标和训练数据目标之间的误差会越来越小， 刚开始时验证和测试目标之间的误差也会变小，可随着训练的增加，测试的误差继续变小，验证的误差反而会有所上升。当验证的误差连续增加到9 时， 为防止过度拟合， 训练停止，训练状态图如图5 所示：

图4 神经网络训练性能图

图5 神经网络训练状态图

仿真表明， 该模型对排粮电机转速预测误差在-5~5 r/min，BP 神经网络预测输出以及训练误差如图6、图7 所示：

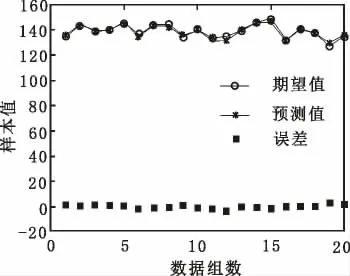
图6 BP 神经网络预测输出

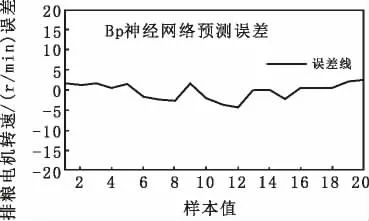
图7 BP 神经网络预测误差

该模型性能评价指标如表1 所示：

表1 神经网络评价指标

3 结语

本文探讨了粮食干燥含水率预测数学模型，薄层干燥中的Page 模型适用于玉米干燥过程，并依此理论搭建了烘干塔物理模型。 针对玉米干燥过程中的复杂非线性关系， 本文成功搭建了BP 神经网络预测模型，预测中将玉米初始入机含水率、干燥热风温度和玉米入机温度作为输入量， 通过预测排粮电机转速作为输出量，预测结果与农场实际值作对比，研究表明排粮电机转速每分钟预测误差在-5~5 r/min 之间， 预测值和实际值相关系数R 为0.98419，该模型能够对玉米出机含水率做有效预测。