基于子程序二次开发的双向曲率板应变分布计算方法
2022-09-06蔡向东赵耀魏振帅常利春
蔡向东,赵耀,魏振帅,常利春
华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
0 引 言
船舶双向曲率板成型的本质是提供目标形状需要的应变成分。在实际成型的过程中需要考虑:由平板到目标形状的应变分布;什么样的成型工具和加载方案可以提供目标形状需要的应变。应变分布是连接变形形状和加载方案之间的桥梁,计算机可以根据应变分布的数据生成机器可以执行的加载方案,从而实现双向曲率板的自动化成型。可以看出应变分布的计算是船舶双向曲率板自动化成型过程中的重要内容,因此提高应变分布的计算精度具有重要意义。
大量科研工作者的研究[1-3]表明,线成型加工产生的应变分布与加工路径之间具有明显的关系:面内应变及面外应变的主应变方向与加工路径垂直。据此提出一种自动化成型方案[1-2,4-6]:首先计算初始平板到目标形状的应变分布,然后根据应变分布确定加工路径,最终根据设计路径上的应变确定加工参数。
在上述自动化成型方案中,首先需要根据目标形状计算应变分布,因此应变分布的计算精度直接影响到后续加工路径和工艺参数的准确性。根据目标形状计算应变分布主要有力学计算方法和微分几何方法。Cheng 等[1]指出利用微分几何方法通常只能得到面内应变分布,很难得到面外应变分布,而基于力学的计算方法可以同时准确计算面内应变和面外应变的分布;Liu 等[2]使用接触算法,将目标形状的板置于2 块刚性平板之间,设置无摩擦接触,调整2 块刚性平板之间的距离等于板厚,将目标形状压平,将应变数据符号反号,可获得初始平板到目标形状的应变分布,但是接触分析计算效率低,而且容易不收敛;Ueda 等[4-6]使用弹性大变形有限元方法计算初始平板到目标形状的应变分布,但是具体的计算过程没有提及;胡昌成等[7]通过直接施加位移场的方式将位移载荷施加到平板上计算位移场,从而获得目标形状的应变分布,该方法只在目标形状曲率较小时适用,在目标曲率较大时直接施加位移场计算的应变分布不准确;Yu 等[8]提出了一种基于非线性优化的双曲面展开算法,通过求解一个有约束的非线性规划问题得到最小面内应变的分布,但是该算法无法计算面外应变的分布;Shin 等[9]提出了板材变形的运动学分析方法:面内应变由初始板和目标曲面的映射展开关系决定,面外应变直接来源于目标曲面的主曲率。由于复杂曲面的展开及其主曲率计算困难,因而该方法实际运用过程中计算量大,计算效率较低。
本文将讨论直接施加位移场和模具接触分析这2 种方法计算应变分布的局限性,将从以下几个方面对应变分布的计算方法进行研究:使用ABAQUS 子程序DISP 进行二次开发,改进了位移场的加载方式,提高了位移场计算精度,从而能准确获取应变分布;考虑到实际加工过程是弹塑性的变形过程,因而讨论了材料非线性对应变分布的影响;考虑到计算效率和计算精度之间的矛盾关系,对几种计算应变分布方法的适用性进行讨论,根据目标形状的曲率半径选取合适的计算方法来提高计算效率,同时满足计算精度的要求;最后通过实例验证子程序方法对于计算船舶典型双向曲率板应变的准确性。
1 基本理论
1.1 变形与应变的关系
船舶双向曲率板成型的本质是将塑性变形施加到初始平板上来获得目标形状,在由初始板变为目标板的过程中,应变是常用控制要素,可以精确地表征物体的相对变形,因此获得应变与变形之间的关系非常重要;船舶双向曲率板成型属于薄板大挠度问题,基于薄板的大变形理论,其变形与应变的关系为

式中:x,y,z分别为板的长度方向、宽度方向、厚度方向;u,v,w分 别为x,y,z方 向的位移; ε和 γ及其下标分别表示某一个方向的轴向应变和剪应变。
1.2 面内应变与面外应变
通过有限元计算可以获取初始平板到目标形状的应变分布,计算得到的应变可以分解为面内应变和面外应变。面内应变是沿着板厚方向均匀分布的应变,面外应变是沿着厚度方向线性变化的应变[10],通过式(2)和式(3)可以计算各个方向的面内应变成分和面外应变成分。
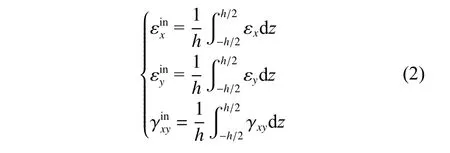

1.3 主应变的计算
目前主要是根据面内主应变和面外主应变的大小和方向来确定加工路径和工艺参数,因此需要对主应变进行计算。可以根据式(2)和式(3)计算得到的面内应变成分和面外应变成分,按照式(4)计算得到面内应变或面外应变的第一主应变和第二主应变。

由式(1)可知,应变是几何性质的表现,仅仅涉及变形的大小而与材料的力学参数无关,在计算曲面板的应变分布时可通过式(1)计算获得,然而实际成型过程中,板的曲面表达为离散的点,基于数学公式的推导过程复杂,因此本文采用大变形有限元对计算应变分布的方法进行研究。
2 应变分布计算方法及比较分析
2.1 局限性分析
根据目标形状计算应变分布有力学计算方法和微分几何方法。微分几何方法通常只能计算得到面内应变,而力学计算方法能同时得到面内应变和面外应变的分布,在计算应变分布方面具有一定的优势,本文只针对力学计算应变分布的方法进行研究。
目前力学获取应变的方法有直接施加位移场进行力学计算和使用刚体模具进行接触计算这2 种方法。从式(1)可以看出:应变分布与形状具有一一对应的关系,应变分布计算的准确性取决于位移场计算结果的准确性;为了方便对计算方法进行描述,将上述2 种方法分别命名为直接施加位移场和模具施加位移场的计算方法。图1 为直接施加位移场计算应变分布的示意图,RP为参考点;图2 为模具施加位移场计算应变分布的示意图。直接施加位移场是根据目标曲面散点的坐标拟合目标曲面,根据目标曲面计算每个节点z方向的位移,将z方向的位移作为边界条件进行计算;模具施加位移场是根据目标形状建立刚体模具,将平板置于2 个刚体模具中间,调整模具间的距离等于板厚,使用接触算法进行计算。
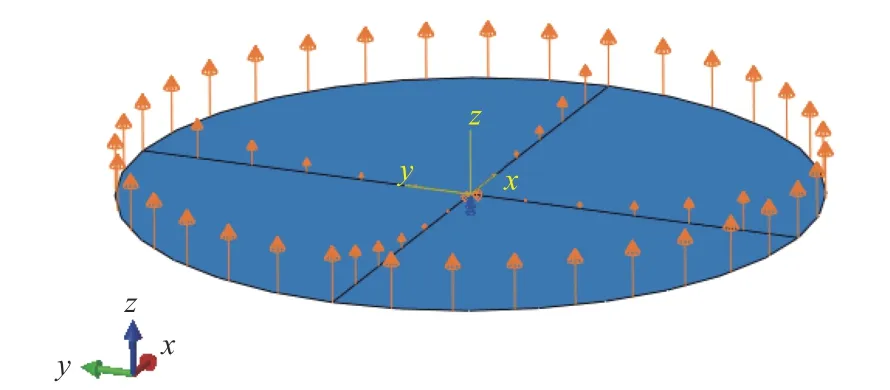
图1 直接施加位移场方法Fig. 1 Direct displacement field application
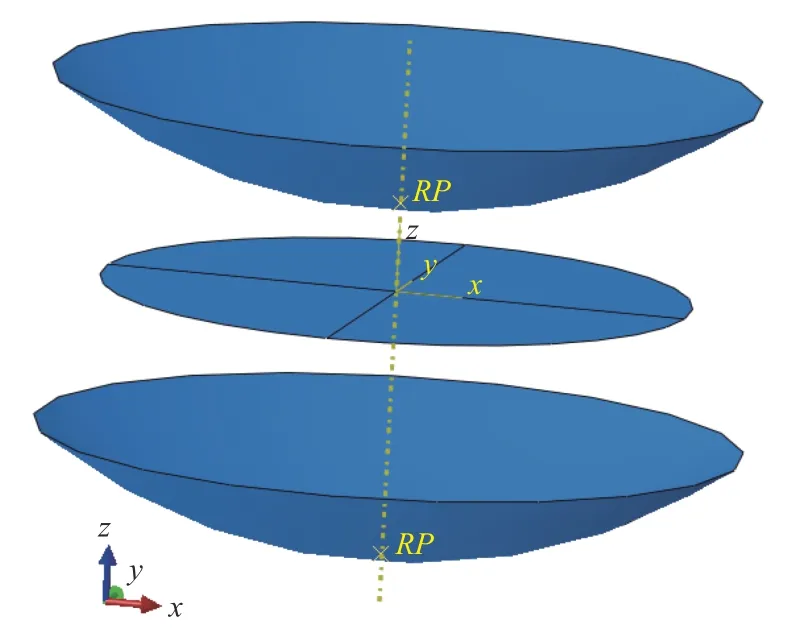
图2 模具施加位移场方法Fig. 2 Mould displacement field application
图3 所示为目标曲面的曲率半径R分别为1.5,3.0 和4.5 m 时,2 种计算方法得到的曲面中心截面处的位移场计算结果。可以看出:曲率小时,直接施加位移场计算得到的形状与目标方程很接近,应变的计算结果满足要求;曲率大时,计算得到的形状与目标形状的方程出现较大的偏差。产生这种现象的原因是:z方向位移场是根据初始节点的坐标计算得到,大变形时节点的x,y位置发生较大偏移,而计算过程中每个节点的z值不会发生改变,导致计算的曲面与目标曲面发生偏离;模具施加位移场的方法在计算精度上可以满足要求,但在建模的复杂程度和计算效率上存在明显的不足。
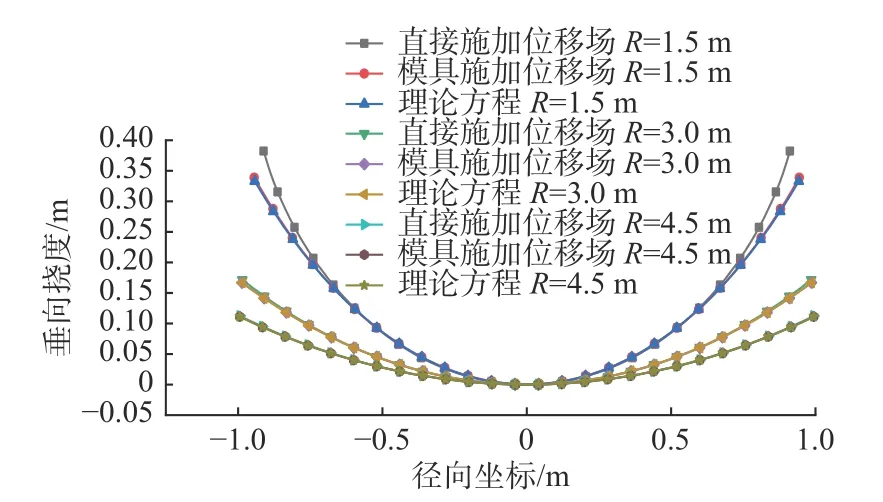
图3 位移场计算结果Fig. 3 Calculation results of displacement field
2.2 子程序施加位移场的计算方法
由于目前准确计算位移场的方法在计算精度和计算效率方面还存在局限性,使用ABAQUS 子程序DISP 进行二次开发,改进位移场的加载方式,可以准确获取目标形状的位移场,从而获取准确的应变分布。为了方便描述,将该方法命名为子程序施加位移场的计算方法。子程序施加位移场的计算方法是根据目标形状拟合曲面,逐步施加位移场载荷,每个载荷步计算结束后获取节点当前坐标,根据当前坐标重新计算位移载荷,可以使计算的形状接近目标形状,使计算的应变结果满足要求。图4 所示为子程序施加位移场的流程,子程序的主要作用是更新当前节点坐标、根据当前节点坐标计算节点位移场。图中:h为总步长; Δh为计算允许的最大步长,用来控制计算精度; Δh′为有限元自动生成步长;k为累计步长。
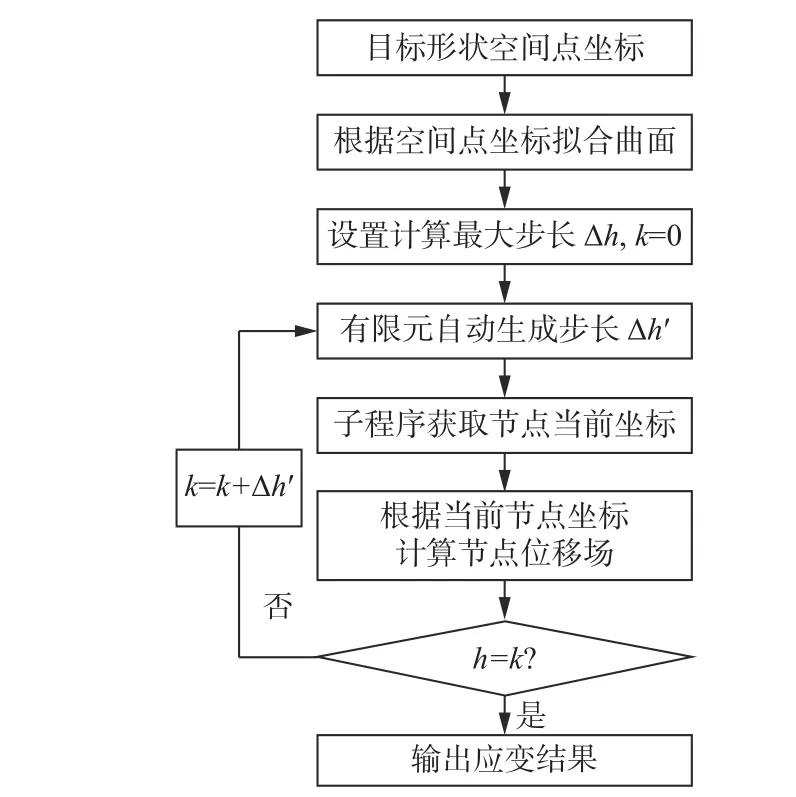
图4 子程序计算位移场流程Fig. 4 The flow of calculating displacement field using subroutine
2.3 比较分析
为了比较这3 种计算方法的计算精度和计算效率,选取半径为r=1 m,板厚t=0.02 m 的圆形平板施加位移场,由于目标曲面曲率半径R=1.5 m时位移场的结果存在明显差异,因此选取目标曲面曲率半径R=1.5 m 对子程序计算方法进行验证。使用3 种方法进行弹性大变形计算,计算结果如图5 所示。从计算结果看,直接施加位移场的方法相对于目标形状会出现明显的偏差;模具施加位移场与子程序施加位移场都能很好地接近目标形状;同时比较了3 种计算方法的效率,表1所示为3 种方法在相同计算条件下的计算时长,子程序施加位移场的计算效率只是略低于直接施加位移场的计算效率,远高于模具施加位移场的计算效率。考虑建模的复杂性以及计算的效率,子程序施加位移场的方法具有明显优势。
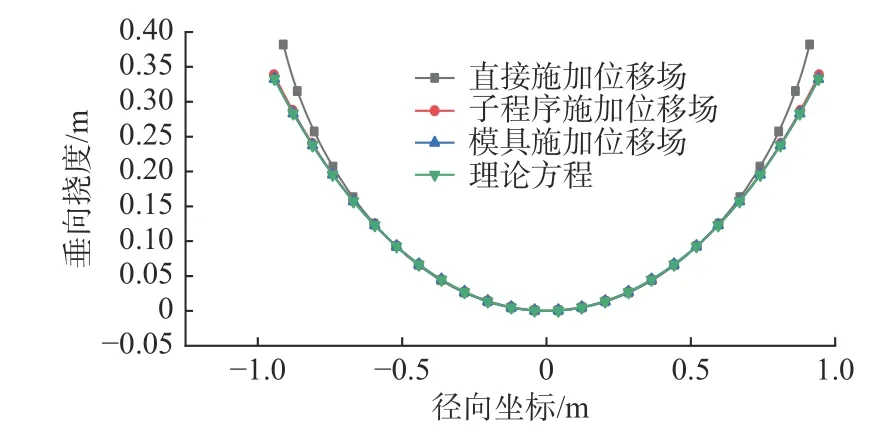
图5 位移场计算结果Fig. 5 Calculation results of displacement field

表1 直接施加位移场、子程序施加位移场和模具施加位移场三种方法计算时长的比较Table 1 Comparison of the calculation times for the three methods: direct displacement field application, subroutine displacement field application and mould displacement field application
3 材料非线性对应变分布的影响
船舶双向曲率板实际成型的过程是弹塑性的过程,在讨论获取应变计算方法的同时应该讨论材料非线性对应变分布的影响。通过前面的计算,基于子程序方法具有计算简单且满足计算精度要求的优点,因此选取该方法来讨论材料非线性对应变分布的影响。
选取模型尺寸为半径r=1 m,板厚t=0.02 m 的圆形平板,目标曲面为曲率半径R=2 m 的球型壳,材料为Q235 钢,使用各向同性硬化模型,其弹性阶段以及塑性阶段的参数见表2[11]以及表3[12]。在该模型上分别进行弹性大变形计算和弹塑性大变形计算,比较两者应变分布场的差异。

表2 Q235 钢材料参数Table 2 Q235 steel material parameters

表3 Q235 钢塑性应力-塑性应变数据Table 3 Data of Q235 steel plastic stress-plastic strain
根据式(3)将应变数据分解为面内应变与面外应变,按照式(4)计算主应变的大小和方向,绘制其主应变的矢量图,由于模型的对称性,只绘制了1/4 模型的结果。图6 和图7 所示分别为弹性和弹塑性计算的面内应变分布,从图中可以看出二者应变分布的形式与分布规律相似。由于模型的对称性,只提取模型对称线位置上的面内主应变的值进行对比,如图8 与图9 所示。弹性和弹塑性计算的周向面内应变分布在数值上接近,弹性和弹塑性计算的径向面内应变的分布有一定的差异。由于材料的非线性,导致2 种计算方法的面内位移分布不一样。图10 所示为面内位移分布,由式(1)可以得知,径向面内位移分布不一样会导致应变分布的不一样。如图9 所示,面外应变的值均位于0.004 9~0.005 1,接近面外应变理论值t/2R=0.005。
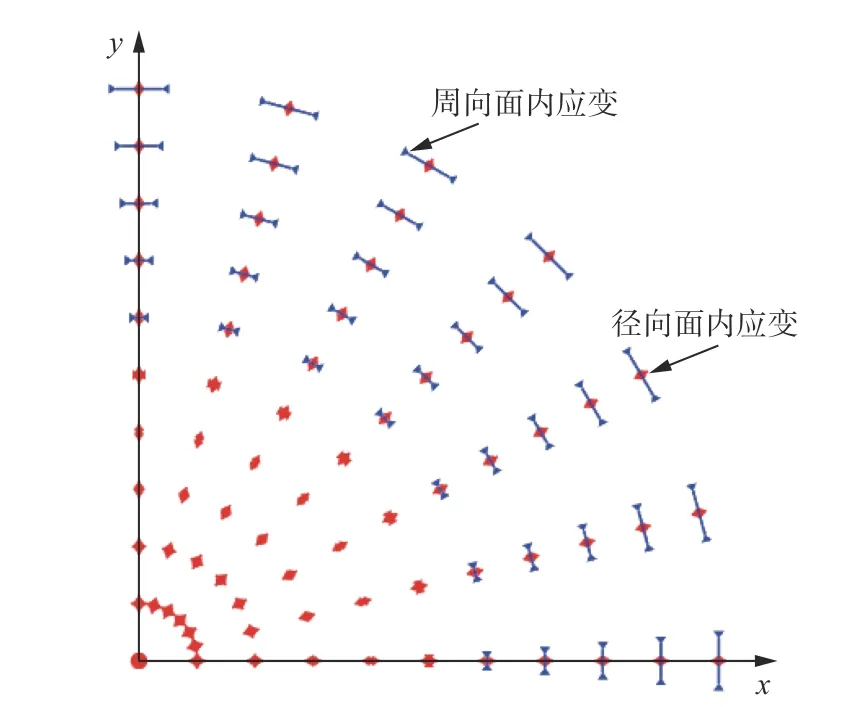
图6 弹性大变形计算面内应变分布Fig. 6 In-plane strain distribution of elastic calculation
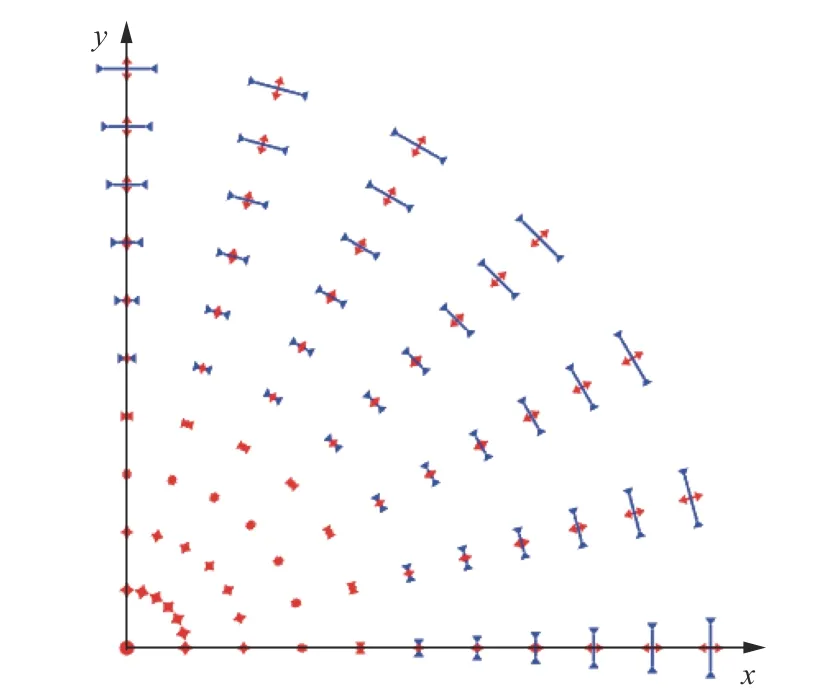
图7 弹塑性大变形计算面内应变分布Fig. 7 In-plane strain distribution of elastoplastic calculation
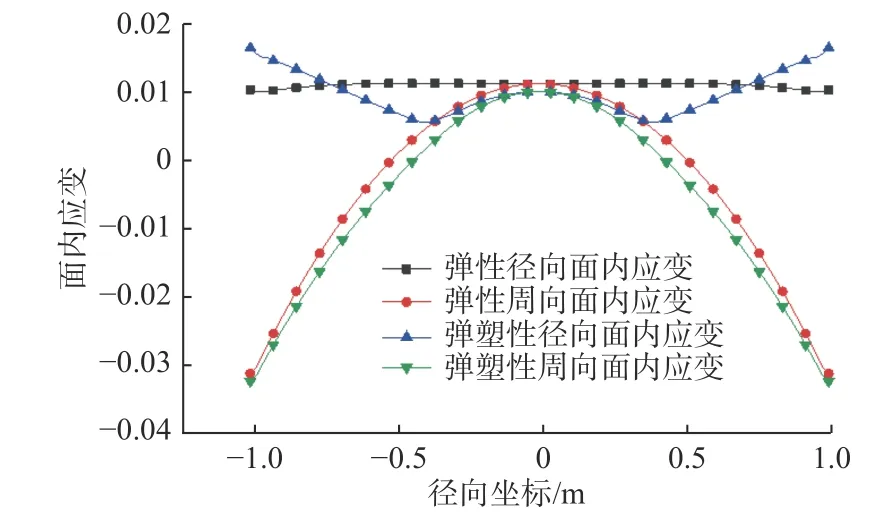
图8 面内应变分布曲线Fig. 8 Distribution of in-plane strain
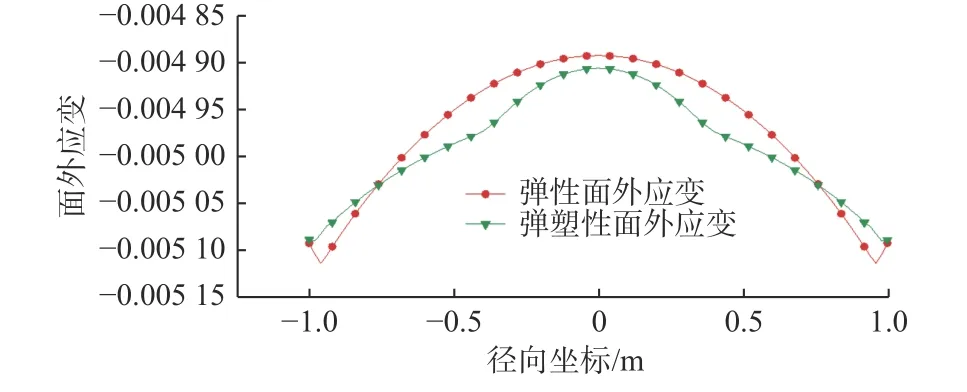
图9 面外应变分布曲线Fig. 9 Distribution of out-plane strain

图10 面内位移分布曲线Fig. 10 Distribution of in-plane displacement
弹性大变形计算与弹塑性大变形计算的面内应变分布结果有一定的差异,根本原因是这2 种计算方法得到的变形位移场存在细微的区别,而这2 种计算方法得到的位移场均接近目标形状,满足船舶制造精度要求,因此它们得到的应变分布图均能作为指导加工的依据。而实际加工很难做到一次成型,会涉及多次应变的计算,考虑到计算的效率,建议使用弹性大变形的计算方法来计算应变。
4 适用性分析
船舶双向曲率板的实际成型过程中,很难做到一次成型,实际成型过程中会多次计算应变的分布,计算的效率会直接影响实际加工的总时长,因此对于应变计算方法的选取要处理计算精度和计算效率之间的矛盾,在保证计算精度的同时,尽量选取计算效率高的方法。
前文讨论了3 种方法的计算精度,可以看出模具施加位移场和子程序施加位移场的计算精度相当,直接施加位移场的方法在曲率较大时会出现较大的误差。从建模复杂程度以及计算效率的角度来看,直接施加位移场的方法建模最简单、计算效率最高;子程序施加位移场的方法建模简单,计算效率高;模具施加位移场的方法建模最复杂,计算效率远低于前2 种计算方法。实际加工过程中可能会涉及多次应变分布的计算,因此计算效率是一个重要的因素,会影响实际加工的总时长,因此不建议使用模具施加位移场的方法。
直接施加位移场和子程序施加位移场在目标曲面曲率较小时计算的位移场结果接近,为了提高计算效率,可以确定一个曲率半径的临界值,曲率半径小于临界值时使用子程序的计算方法,曲率半径大于临界值时使用直接施加位移场的计算方法。选取半径r=1 m,板厚t=0.02 m 的圆形平板为研究对象,对于不同曲率半径的目标曲面进行计算,设置目标曲面的曲率半径分别为2,4,6,8 和10 m,该系列曲率半径几乎涵盖90%以上的船舶双向曲率板。选取面内应变与面外应变的最大值作为目标,如图11 和图12 所示,当曲率半径大于6 m 时,面内应变的最大值与面外应变的最大值误差在5%以内,这意味着曲率半径大于6 m时,可以使用直接施加位移场方法,从而提高计算效率。
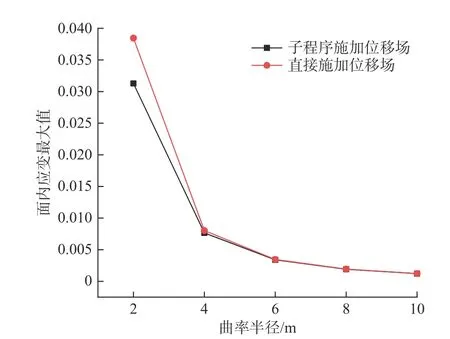
图11 曲率半径与面内应变Fig. 11 Radius of curvature and in-plane strain
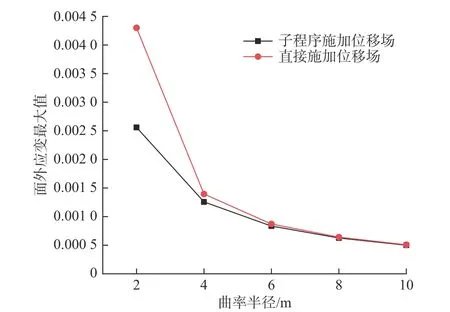
图12 曲率半径与面外应变Fig. 12 Radius of curvature and out-plane strain
5 实例验证
上文的主要研究对象为圆形平板,为了证明计算方法的有效性,选取矩形平板为研究对象,对理想形状的马鞍型和风帆型进行了计算,矩形板尺寸为2 m×1 m×0.02 m,杨氏模量为2.1×1011Pa,泊松比为0.3。马鞍型的目标形状方程为z=-0.1x2+0.5y2,风帆型的目标形状方程为z=0.1x2+0.5y2, 2 个 目 标 形 状y方 向 和x方 向 的 曲率半径分别为1 和5 m,该曲率半径满足船舶上大曲率板的要求。选用模具施加位移场和子程序施加位移场2 种方法进行弹性大变形计算,以模具施加位移场的计算结果为标准,验证了子程序施加位移场的准确性。图13 所示为使用模具施加位移场方法计算得到的马鞍型板的面内和面外主应变分布,图14 所示为使用子程序方法计算得到的面内和面外主应变分布,二者的分布规律一致。图13 和图14 中标注了2 种计算方法的主应变最大值 |max|,经过对比可知,2 种计算方法的面内主应变相对误差在4%以内,面外主应变的相对误差在1%以内。图15 所示为使用模具施加位移场方法计算得到的风帆型板材的面内和面外主应变分布,图16所示为使用子程序方法计算得到的面内和面外主应变,二者的分布规律一致。同样,根据图15 和图16 所标注的主应变最大值可知,2 种计算方法的面内主应变的相对误差在3%以内,面外主应变的相对误差在2%以内。这2 种典型形状的计算结果进一步说明了子程序施加位移场计算方法的准确性。其中最大误差的位置在板材的中间区域。产生误差的主要原因在于:子程序计算方法是通过逐步施加位移场逼近精确的位移场,计算结果的精度与选取的计算步长有关系。
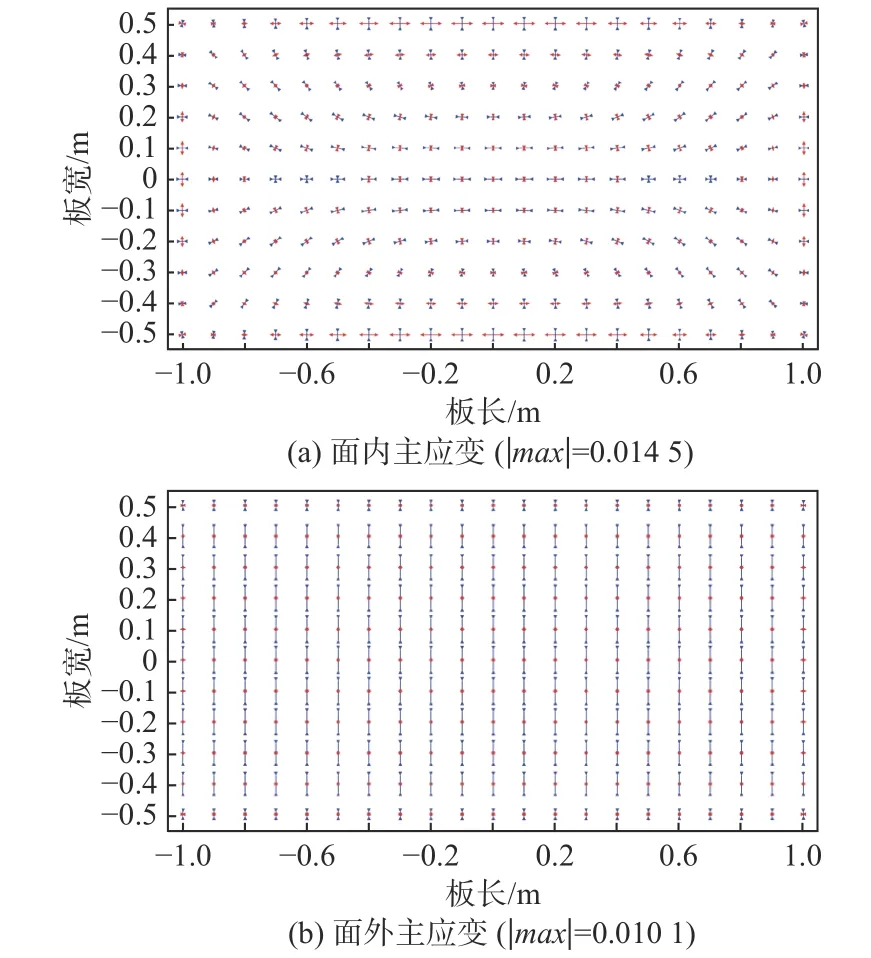
图13 模具施加位移场方法计算的主应变分布Fig. 13 Principal strain distribution calculated by mould displacement field application
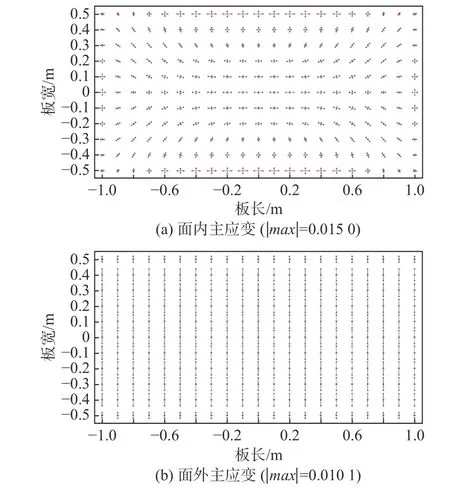
图14 子程序施加位移场方法计算的主应变分布Fig. 14 Principal strain distribution calculated by subroutine displacement field application
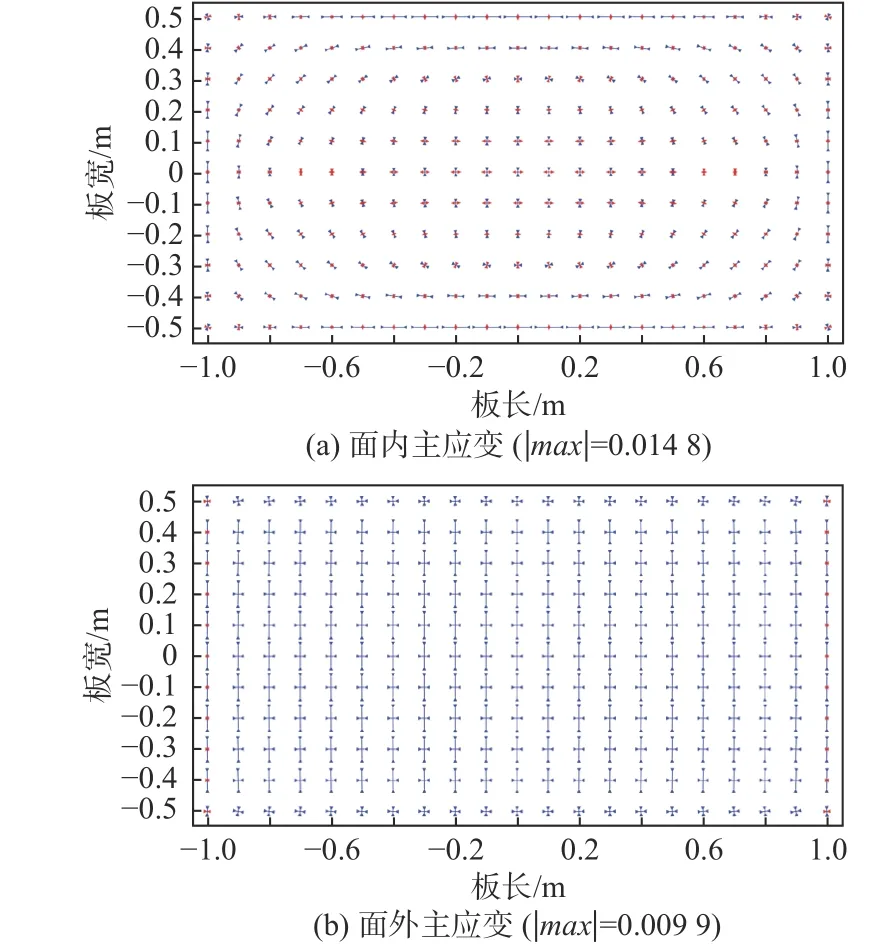
图15 模具施加位移场方法计算的主应变分布Fig. 15 Principal strain distribution calculated by mould displacement field application
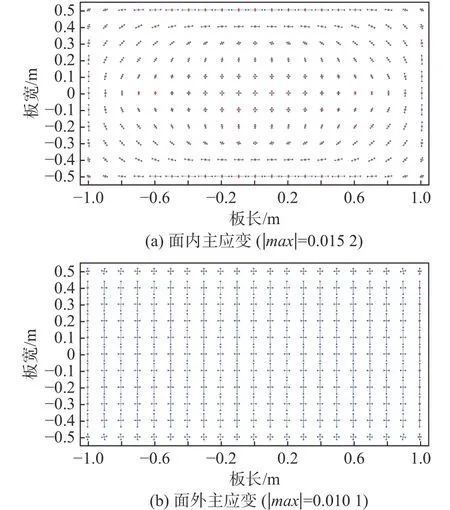
图16 子程序施加位移场方法计算的主应变分布Fig. 16 Principal strain distribution calculated by subroutine displacement field application
6 结 论
本文指出了目前力学获取应变方法的局限性,使用ABAQUS 子程序进行二次开发,改进了位移场施加的方法,提高了应变分布的计算精度,并讨论了材料非线性对应变分布的影响,对于各种计算方法的适用性进行了分析。通过本文研究得出了以下结论:
1) 目标形状的曲率较大时,使用直接施加位移场的方法会导致位移场的计算结果不准确,使用模具施加位移场的方法建模复杂,计算时间长,子程序施加位移场的方法能很好解决建模复杂和计算时间长的问题。
2) 材料非线性会导致弹性大变形与弹塑性大变形计算的位移场结果出现细微的差别,导致应变分布出现差异,但应变分布规律基本一致,考虑到计算的效率,建议使用弹性大变形的计算方法来计算应变。
3) 目标形状的曲率较小时,直接施加位移场与子程序施加位移场计算的位移场结果差异很小,可以使用直接施加位移场的方法来获取应变,提高计算效率。
