海上无人系统时间协同航迹规划
2022-09-06尹逢川梁晓龙陶浩侯岳奇齐铎吴贤宁
尹逢川,梁晓龙*,陶浩,侯岳奇,齐铎,吴贤宁
1 空军工程大学 空管领航学院,陕西 西安 710051
2 中国舰船研究设计中心,湖北 武汉 430064
0 引 言
自美军于2011 年提出空海一体战以来,随着多域战(multi-domain battle)、多域作战(multidomain operation)等作战概念的递进演变,当前作战环境已不再局限于单一作战域,而是逐步向跨域协同、多域融合过渡。近年来,不断发展的无人装备与跨域协同概念相结合,一种新型的作战概念—海上无人系统作战应运而生。然而,制约海上无人系统形成作战能力的关键技术,如通信自组网、协同态势感知、任务分配、航迹规划、编队控制、虚拟测试等还需要进一步发展。
海上无人系统是指由海上无人驾驶、可通过遥控操作或自主行动的机动载具或航行器,以及完成任务所必须的有效载荷和支持组件共同组成的系统,主要包括无人机(unmanned aerial vehicle,UAV)、无人艇(unmanned surface vehicle,USV)和无人水下航行器(unmanned underwater vehicle,UUV)[1]。针对海上无人系统跨域分布的特点,协同航迹规划是其中一项重要的关键技术。海上作战环境复杂,海上无人系统从出发点到达目标区域需穿越敌方雷达、声呐网、水雷区等威胁区,但受限于自身的航速和所使用的燃油,需要在任务实施前规划出一条能够满足所有约束条件的最优航迹,从而提高执行任务的效率。
同构无人集群的路径规划问题涉及高维的等式和不等式约束,以及时空协同的要求。近年来,为了解决这个问题,有学者研究了各种路径规划算法,包括集中避碰规则和时间调整策略[2-5]。算法主要分为2 类:一类为传统方法,例如广义的Tau 理论[6]、动态规划[7]、人工势场法[8]等;另一类是基于种群的进化算法,例如粒子群优化(PSO)算法[9-10]、遗传算法(GA)[11]、萤火虫算法(FA)[12]等。但这些方法多侧重于避障,较少考虑集群内的时空协同。为了解决需要同时到达的航迹规划问题,Liu 等[13]提出了4D 航迹规划方法,即在三维中加入时间维度,为解决带有强时间约束的多UAV 航迹规划问题提供了新的思路,但却没有考虑航迹点数量对规划成功率的影响。黄书召等[14]在其仿真结果中展示了航迹点数量对航迹规划成功率的影响,但未针对产生该影响的原因做出解释。
与同构多无人系统之间的协同航迹规划研究相比,针对异构多无人系统协同航迹规划研究的报道较少。在复杂环境下,侯岳奇等[15]量化了对空海等各类障碍和威胁并建立二维数学模型,然后在众多内外约束下,使用差分进化(DE)算法完成了由UAV 和USV 构成的异构集群的协同航迹规划。Wu[16]提出了一种UAV 和UUV 协同搜索跟踪水下目标的协同框架与跟踪算法。在海上无人系统内,平台间的跨域通信能力较弱,UAV 与UUV 要直接进行通信很困难,因此,UAV,USV和UUV 的跨域协同成为一个解决跨域通信的方法。Wu 等[17]提出了一种UAV,USV 和UUV 协同通信和搜索的框架,其中USV 为空中与水下通信的中继,可更高效地完成水下目标搜索追击任务。
由上述研究情况可以看出,现有的方法主要集中在解决同构平台的航迹规划,以及满足异构平台协同所需要的通信距离约束上,而较少考虑航迹点数量对航迹规划成功率的影响,以及由UAV,USV 和UUV 构成的海上无人系统到达目标区域的时空协同问题。在一些典型的任务中,例如多域饱和攻击水面目标任务,如果平台没有同时到达阵位,目标有可能会逃逸,从而使攻击任务失败。这类任务就对各个平台的时空协同提出了较高要求。
对于海上无人系统时间协同航迹规划问题,本文将首先针对海上静止目标多域饱和打击任务,对空中、水面和水下的自然威胁以及敌方威胁进行建模,设计优化函数,并使用DE 算法完成航迹求解;然后,针对多域饱和攻击任务需要精准的时空协同的问题,为UAV,USV 和UUV 设计出发点不同、目标点相同的时间协同策略并进行仿真实验验证;最后,由仿真结果分析并总结航迹点数量与规划成功率之间的关系。
1 时间协同航迹规划问题建模
1.1 任务背景
在所有环境信息、敌方防卫信息均已知、敌方补给船航迹已被指挥中心获取的情况下,临时指派附近1 架UAV、1 艘USV 和1 艘UUV 组成海上无人系统,分别从(xSA,ySA,zSA),(xSS,ySS,0)和(xSU,ySU,zSU)的坐标位置出发,前往目标攻击阵位攻击敌方补给船。在接到指令前,三者在各自区域执行任务,未携带昂贵的远程制导武器等大规模杀伤性武器。为彻底破坏该敌方目标,防止目标逃逸,三者需要分别从空中、水面和水下同时对目标船发动攻击,在平台资源和武器资源一定的情况下获取最大效费比。另经侦察,已知目标船的吨位较大,不易转弯,当前位置坐标为(xT0,yT0,zT0), 航速为VT0。 假定目标船航速VT0保持不变,故在攻击任务开始前,根据环境及平台约束,需为这3 个无人平台规划出一条能同时安全到达目标攻击阵位的航迹,并给出出发时刻和巡航速度。
1.2 问题描述
由上述背景分析可知,UAV,USV 和UUV 在接到任务后是从不同起点出发的,为摧毁目标,需要同时到达目标点附近的攻击阵位。图1 所示为协同航迹规划示意图。
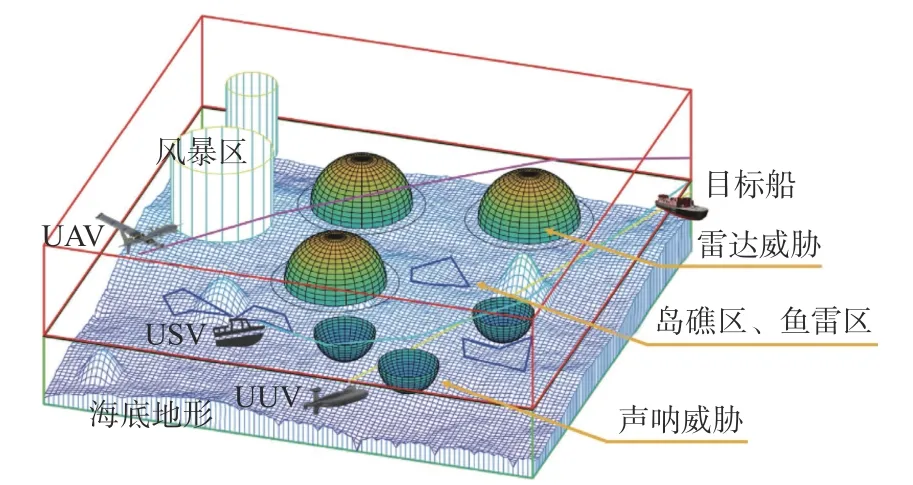
图1 海上无人系统协同航迹规划示意图Fig. 1 Schematic diagram of cooperative path planning for UMS
在上述任务背景及假设下,可根据目标船当前位置和速度信息选择其航迹上的一个点作为伏击点p, 即终点pF。 在此问题中,起点pS和终点pF已 知,因此可在pS和pF之间插入有限个点生成航迹点,再将起点pS、 航迹点序列WP和 终点pF按顺序连接即生成航线P。此时,UAV,USV 和UUV 的 航 迹 分 别 为PA,PS,PU,起 点 分 别 为pAS,pSS,pUS, 终点分别为pAF,pSF,pUF,航迹点序列分别为WPA,WPS,WPU。综合考虑自然环境约束和敌方的威胁约束,通过优化算法求解出三者的最优航迹集合P*,如式(1)所示。
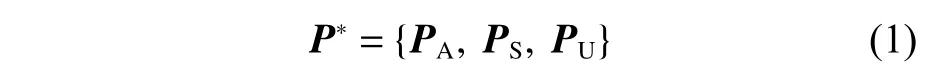
其中:

式中,WPA,WPS,WPU包含的航迹点数量可以不同。在三维空间中,海上无人系统协同航迹规划问题就是用一组优化准则和约束为每个平台规划出一条航行代价最小的可行航迹。在同时到达目标位置的前提下,规划的航迹满足环境、威胁、自身运动性能约束,且航迹平滑、航程更短。
1.3 问题建模
UAV,USV 和UUV 三者航迹优化的指标通常包括航程的累计值J1、爬升和下降角的累计值J2以 及转弯角的累计值J3,航迹规划需要满足的约束可以分为时间约束P1、 自然环境约束P2、敌方威胁约束P3、 爬升和下降角约束P4及转弯角约束P5,优化目标函数如式(2)所示。精准的时空协同需各无人平台能同时到达攻击阵位,满足时间约束P1,也即三者到达终点的时间误差小于设定值ε。UAV,USV,UUV 到达终点的时间点分别表示为tA,tS和tU,如式(3)所示。
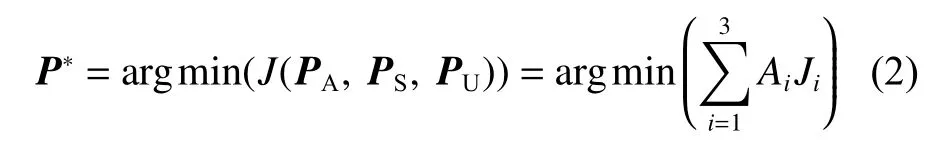
其中,
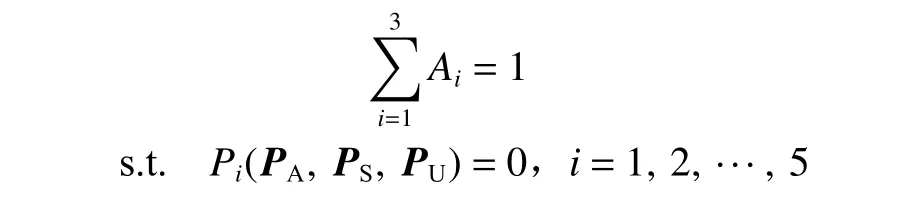
式中:Ai为 第i个 优化指标 系数;Pi为 第i个约束条件,其中Pi=0表 示满足约束条件,Pi>0表示不满足约束条件。以时间约束为例,其惩罚计算如下:
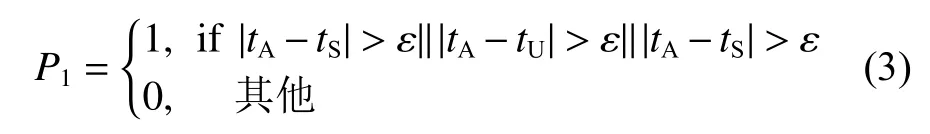
若要解决海上无人系统的时间协同航迹规划问题,还需对自然环境约束和敌方威胁约束进行适当建模,构建符合现实需求的航迹优化函数,并通过优化算法求解出满足约束的航迹。
1.4 场景建模
海上无人系统除了需要在划定的任务区域内航行外,还要能够避免穿过类似岛礁等的禁入区和敌方雷达等的威胁区。
UAV 在指定空域,即禁出区VAF内飞行,将面临的主要自然威胁是风暴区VA,紊乱的气流会严重影响飞行,甚至造成机体损毁,所以航迹规划应避免穿越风暴区。此外,UAV 还将面临的主要敌方威胁是雷达探测区VAT。因此,对空域建模时采用长方体描述禁出区的边界,如式(4)所示。鉴于实际的风暴区与雷达威胁区的空间几何形状差别较大,为了简化模型同时又贴近实际,使用圆柱体描述风暴区的边界,如式(5)所示。根据雷达探测的特性,使用半球形描述敌方雷达威胁的边界,如式(6)所示。
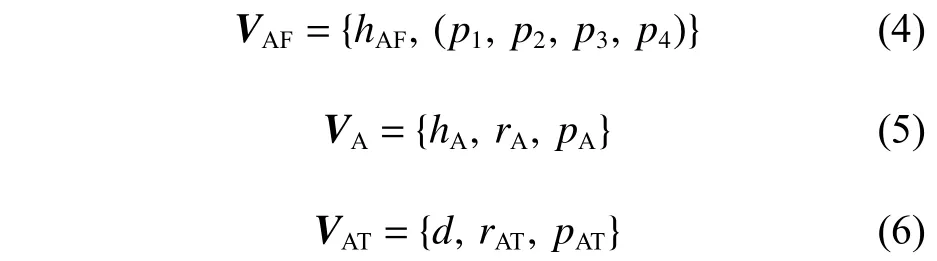
上式中:p1,p2,p3,p4分别为用长方体描述的禁出区和与xoy面平行的下底面上按顺时针排列的4 个坐标;hAF为 长方体的高;pA为用圆柱体描述的在xoy面圆心的坐标;rA为圆柱体半径;hA为圆柱体的高;pAT为 半球在xoy平面圆心的坐标;rAT为半球坐标;d=1, 表示半球分布在z>0的区域。
USV 在指定海面区域,即禁出区VSF内航行,会受到风暴区的影响,风暴区的模型如式(5)所示。此外,USV 还面临着暗礁威胁和敌方布置的水雷区VST威胁,以及敌方探测威胁,即雷达探测区VS。因此,对水面域建模时分别采用长方形描述禁出区边界,多边形描述鱼雷区和岛礁边界,圆形描述敌方雷达威胁边界,如式(7)如~式(9)所示。上式中:pS1,pS2,pS3,pS4分别为禁出区按顺时针排列的4 个顶点坐标;rS为雷达探测区半径;pS为 雷达探测区圆心的坐标;m为多边形顶点个数;p1,p2,···,pm为禁入区按顺时针排列的顶点坐标。
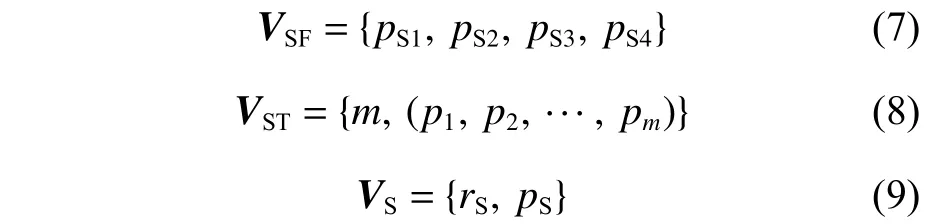
UUV 需要在指定水下区域,即禁出区VUF内航行,其面临的主要自然威胁是海底的起伏地形,由规则格网数字高程模型(digital elevation model,DEM)记录存储,面临的主要敌方威胁是敌方声呐探测区VUT。因此,对水域建模时采用长方体来描述禁出区边界,如式(10)所示;采用半球形来描述敌方声呐威胁边界,如式(11)所示。
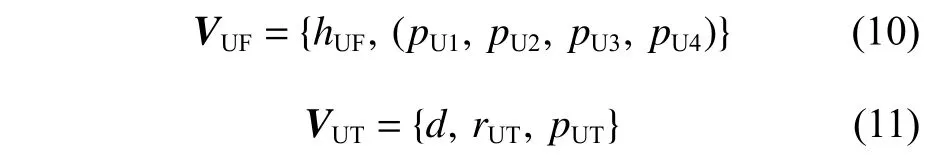
上式中:pU1,pU2,pU3,pU4分 别为长方体与xoy面平行的下底面上按顺时针排列的4 个坐标;hUF为长方体的高;pUT为 声呐探测区在xoy平面圆心的坐标;rUT为 声呐探测半径;d=-1,为声呐探测区分布在z<0处的区域。
1.5 航迹建模
对于随机分布的航迹点,搜索空间太大,但采用如下航迹点生成方式则可减小搜索空间。将起点和攻击阵位点投影到xoy平面,然后在xoy平面上画出从起点到攻击阵位点的线段L。 线段L被N个点平均分为N+1 段,并绘出经过每个点且垂直于x轴的直线,表示为 {L1,L2,···,LN}。航迹建模示意图如图2 所示。
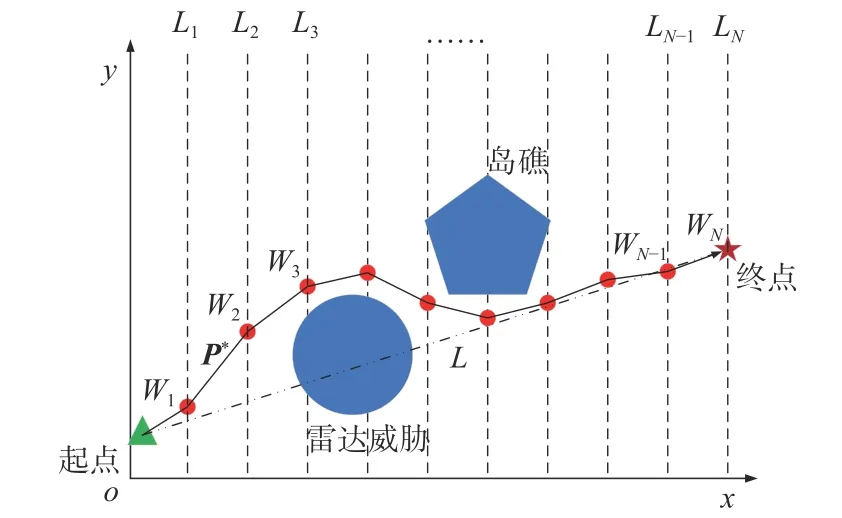
图2 航迹建模示意图Fig. 2 Schematic diagram of path modeling
如图2 所示,航迹点Wi(i=1,2,···,N)的投影在垂线Li(i=1,2,···,N)上,除x轴以外,其他维度的坐标需要考虑约束条件后再进一步予以确定。最后,便可形成一组航迹点序列WP=(W1,W2,···,WN)。 按 顺 序 连 接 航 迹 点Wi(i=1,2,···,N) , 即可以构成无人平台的航迹P*。UAV的航迹点数量为N1,生成的航迹点序列可以表 示 为WPA={WPA1,WPA2,···,WPAN1}。USV的航迹{点数量为N2,生成的航迹点}序列可表示为WPS=WPS1,WPS2,···,WPSN2。UUV的 航 迹点数量为N3,生成的航迹点序列可表示为WPU={WPU1,WPU2,···,WPUN3}。在所有步骤完成后,3D 空间内海上无人系统时间协同航迹规划变成一个优化问题,即如何选择航迹点,并让海上无人系统整体上在满足环境约束、运动约束的同时,以最小代价在最短时间内到达各自的攻击阵位。
2 时间协同航迹规划问题求解
时间协同航迹优化目标函数如式(2)所示。仿真求解需要根据场景建模和航迹建模,对优化目标函数和约束条件进行更详细地描述。
2.1 优化指标
2.1.1 航程优化指标
UAV,USV 和UUV 的燃料供应有限,必须在燃料消耗完之前到达目的地。本文采用总的路径长度与到达目的地的直线距离之比来表示燃油的消耗。
由此可见,路径越短,在同等情况下无人平台的燃油消耗越少,到达目标阵位所需时间也越短。而减少它们暴露于复杂环境中的时间,可以降低被未知威胁目标发现的概率。Jdis(A),Jdis(S)和Jdis(U)分别为UAV,USV 和UUV 的实际航程与直线距离之比,如式(12)~式(14)所示。

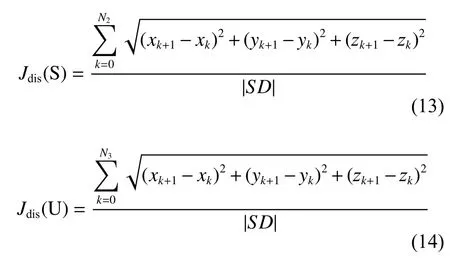
其中,
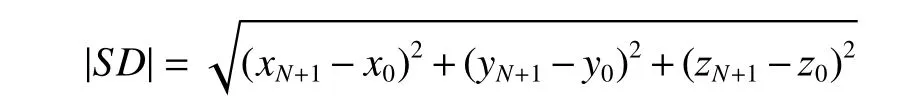
式中,坐标 (x0,y0,z0) , (xN+1,yN+1,zN+1)分别为航迹的起点和终点。若是UAV,N=N1; 若是USV,N=N2;若是UUV,N=N3。
因此,三者的航程优化可由式(15)表示。

2.1.2 UAV 航迹爬升角和下降角航程优化指标
USV 因是在水平面运动,所以不存在航迹的上下起伏问题。UUV 下潜后通常采取定深巡航方式,到达终点才开始上浮,且上升下潜均是在z轴方向直线运动,因而不适宜采用航迹的爬升和下降角度来描述。对于UAV 的航迹,其航迹点k的爬升和下降角 θk在限值之内,并由式(16)计算其累计值,有关 θk的计算见后文。爬升角限值αAk和 下降角限值 βAk分别由式(17)和式(18)计算,单位为rad。 αAk和 βAk与UAV 的飞行高度zAk相关,本文中设为高度1 000 m 时的计算值。

故UAV 航迹的爬升和下降角优化累计值如下:
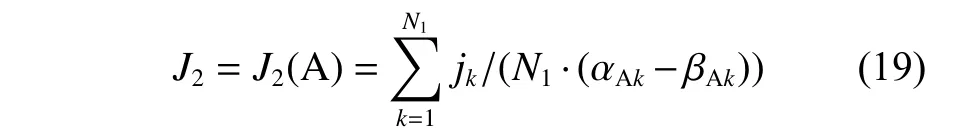
2.1.3 航迹转弯角优化指标
转弯角度越大,能耗越多,例如飞行器的大角度转弯需额外的推力,类似地,船艇需消耗转舵机构的能量,其阻力的增加还需额外的推力,故规划的期望航迹应尽量平滑。本文模型中,理想航迹的转弯角未超过最大值且保持尽量小。图3为转弯角示例图,图中Pk为转弯点,分别用(xk-1,yk-1,zk-1),(xk,yk,zk),(xk+1,yk+1,zk+1)表 示 航迹上连续3 个航迹点的坐标。假设第k个航迹点处的转弯角为 γk(单位:rad),其计算方式如式(20)所示。

图3 转弯角示意图Fig. 3 Schematic diagram of turning angle
其中:
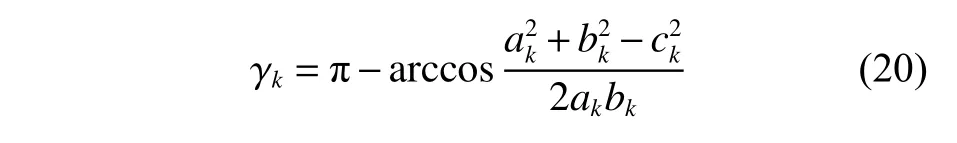
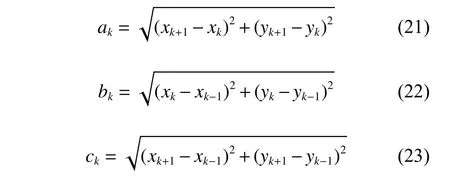
设无人平台的最大转弯角为 γ,转弯角数量为N,无人平台总数为Nvehicle,则航迹的转弯角奖励函数(优化累计值)如式(24)所示。
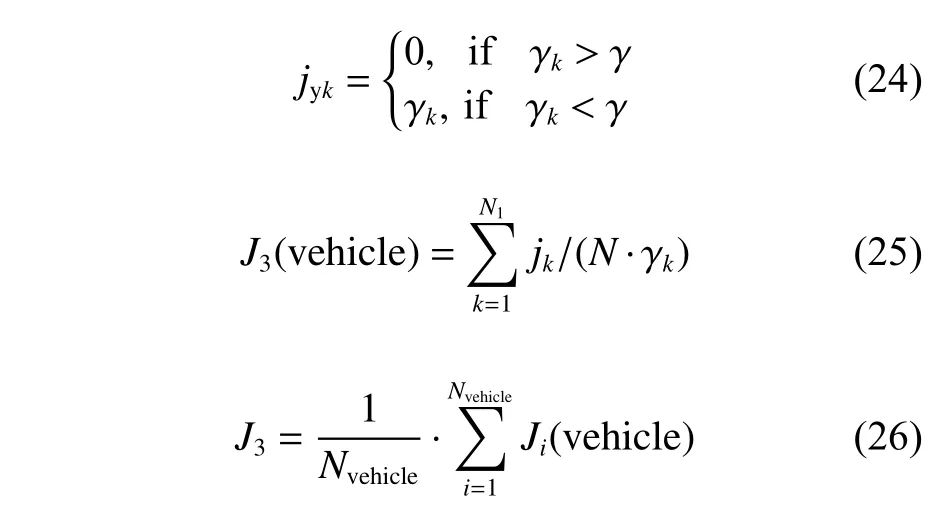
式中,J3,J3(vehicle)分别为单个无人平台和所有平台的转弯奖励函数均值。
2.2 约束条件
2.2.1 时间协同约束
对于饱和攻击任务,UAV,USV 和UUV 需要同时到达目标点附近指定的位置,以便同时发起攻击。鉴于各平台是从不同的起点出发,在规划航迹时,应使它们暴露于威胁中的时间尽可能短。因此,提出如下所述的时间协同策略,以确定各平台的出发时间和巡航速度,从而满足时间协同约束。
如图1 所示,UAV,USV,UUV 分别在空中、海面和水下航行,且各自的速度限值为 [vAmin,vAmax],[vSmin,vSmax],[vUmin,vUmax]。例如,为UAV 规划一条长度LA的航迹,其到达目标攻击阵位的时间区间按式(27)计算,而 最短时间TAmin和最长时间TAmax分别由式(28)和式(29)得到。

与式(27)~式(29)的计算方法类似,可分别得到USV,UUV 到达目标攻击阵位的最短时间TSmin和TUmin。图4 所示为无人平台时间协同策略的示例。其中:到达目标阵位所用时间最长的为UUV,其最先出发,巡航速度为vUmax;UUV 出发T1时 间后,USV 出发,巡航速度为vSmax;UUV 出发T2时 间后UAV 出发,巡航速度为vAmax;在UUV 出发T3时间后,各平台同时到达目标攻击阵位。通过该时间协同策略,海上无人系统可以在最短的时间内到达攻击阵位。
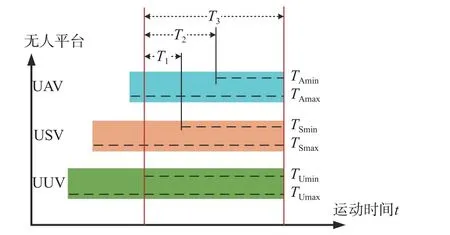
图4 时间协同策略Fig. 4 Time coordination strategy
通过上述策略,同时到达的时间协同约束可以一直被满足。时间协同约束项的值如式(30)所示。
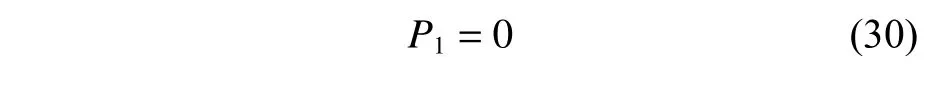
2.2.2 禁入区和禁出区约束
可行的航迹不能穿越障碍物体。在海上作战环境中,USV 和UUV 的主要禁入区是岛礁,UAV 的主要禁入区是强风暴发生地。这里,给出一个合理的假设,即已知所有禁入区的位置、范围等特性。为避免误入禁入区,需设计一个惩罚函数用于定义航迹中某一点进入禁入区的情况。在近海环境下,海底有类似于陆地山脉一样的起伏地形,假设f(xi,yi)为 (xi,yi)处地形的海拔值,(xAj,yAj,zAj) 为 UAV 航迹上的任意一点,(xSj,ySj, 0)为USV 航迹上的任意一点,(xUj,yUj,zUj)为UUV 航迹上的任意一点; ΩA为UAV 航行中的风暴区合集,风暴区用圆柱体表示,即 ΩA=ΩA1∪ΩA2∪···∪ΩAM1,其中M1为 风暴区数量;DS为水面水雷区和触礁区的并集,即DS=DS1∪DS2∪···∪DSM2, 其中M2为水雷与触礁区的数量之和。因此,UAV,USV 和UUV的禁入区惩罚函数分别如式(31)~式(33)所示。

以上式中:H为单个平台规划的航迹中一个点落在禁入或禁出区时得到的惩罚值;P为H的累计值;Ωsk为风暴区在水面的区域合集。
另外,UAV,USV 和UUV 需要在一片指定的区域内航行,在该区域外运行将会受到惩罚。以下给出的是航迹点落到特定区域外时对其进行惩罚的计算公式。

以上式中,VAF,VSF和VUF分别为UAV,USV,UUV的指定航行空间,也即禁出区。
式(31)与式(34)相加表示UAV 的航迹点未满足禁入、禁出区条件时所受的惩罚,如式(37)所示;同UAV,式(32)和式(35)相加,式(33)和式(36)相加分别表示USV 和UUV 所受的惩罚,分别如式(38)和式(39)所示。式(40)表示UAV,USV 和UUV 的航迹不满足禁出、禁入约束时受到的惩罚之和。
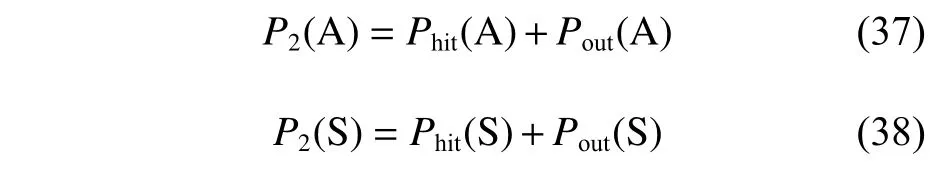

2.2.3 威胁区约束
首先,假设威胁源的类型、位置和范围等信息完全已知。UAV,USV 的威胁源为敌方雷达,UUV的威胁源为敌方声呐。UAV,USV 和UUV 需要远离这些威胁源,否则一旦进入威胁区,就有可能被探测到甚至是被击毁。对UAV 产生威胁的雷达区i(i=1,2,···,H1)的空间模型为一个用向 量VTi=[xATi,yATi,zATi,rATi,LATi]表 示 的 半 球形,其中, [xATi,yATi,zATi]为半球球心的坐标,记为pATi,rATi为 雷达最大探测距离,LATi为对UAV 的威胁系数,该值越大,威胁就越大。敌方雷达具备同时对空对海面的扫描能力,因此对UAV,USV 产生威胁的雷达总数均为H1。对USV 产生威胁的雷达区i(i=1,2,···,H1)的空间模型为一 个 用 向 量VSTi=[xSTi,ySTi,rSTi,LSTi]表 示 的 圆形,其中 [xSTi,ySTi]为 圆心的坐标,记 为pSTi,rSTi为雷达最大探测距离,LSTi为对USV 的威胁系数,该值越大,威胁就越大。对UUV 产生威胁的声呐探测区i(i=1, 2,···,H2)的空间模型为一个用向量VUTi=[xUTi,yUTi,zUTi,rUTi,LUTi]表 示 的 半 球 形,其中, [xUTi,yUTi,zUTi]为 半球球心的坐标,记为pUTi,rUTi为 声呐最大探测距离,LUTi为声呐对UUV 的威胁系数,该值越大,威胁就越大。
UAV,USV 和UUV 在有航段穿入威胁区时,才会受到惩罚。如果UAV 的航迹穿过威胁区,设航迹上距离威胁区i最近的点为pAi=[xAi,yAi,zAi], 其中i=1,2,···,H1,H1为雷达威胁区总数,穿过威胁源i时对UAV 的航迹的惩罚可以采用式(41)定义;如果USV 的航迹穿过威胁区,设航迹上距离威胁区i最近的点为pSi=[xSi,ySi,zSi],其中i=1,2,···,H1,穿过威胁源i时对USV 的航迹的惩罚可以采用式(42)定义;如果UUV 的航迹穿过威胁区,设航迹上距离威胁区i最近的点为pUi=[xUi,yUi,zUi], 其 中i=1,2,···,H1,航迹穿过威胁源时对UUV 的航迹的惩罚可以采用式(43)定义。
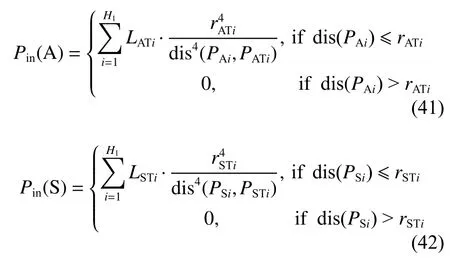

通过上述代价计算,总的代价用采式(47)进行计算。
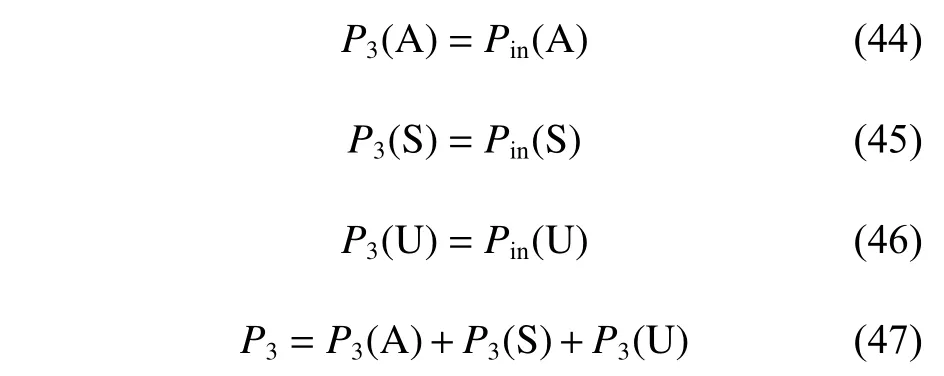
2.2.4 UAV 航迹爬升和下降角约束
UAV 在航迹点k处的俯仰运动受限于最大爬升角 αAk和 最大下降角 βAk,其定义分别如式(16)和式(17)所示。αAk和 βAk与UAV 所在的高度(单位:m)有关。
航迹点k和k+1之 间的线段为航段lk,其中爬升和下降角θk可以采用式(48)计算:
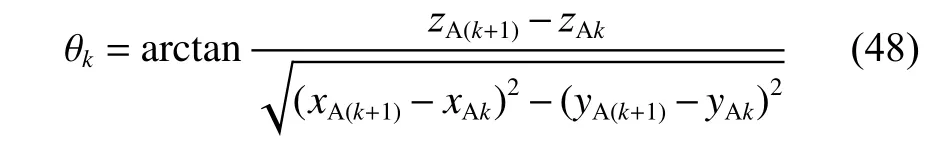
航迹上航段lk的爬升和下降角超出限值时,可以按式(49)进行惩罚值计算:

因此,爬升和下降角的最终惩罚、优化函数如式(50)所示。

2.2.5 航迹转弯角约束
UAV,USV 和UUV 的运动分别受最大转弯角 γA, γS, γU的约束。若规划的航迹转弯角超出限值,平台运动能力会受到限制,使其无法执行规划的航迹。鉴于转弯角越小,航迹越平滑,故在本模型中,理想的航迹转弯角应不超过最大转弯角且应尽量小。分别用(xk-1,yk-1,zk-1), (xk,yk,zk),(xk+1,yk+1,zk+1)表示航迹上连续3 个航迹点的坐标,最大转弯角为 γ 。假设第k个航迹点处的转弯角为 γk, 如式(20)~式(23)所示计算。若第k个航迹点处转弯角超过限值,则如式(51)所示计算其惩罚值pk。

设UAV,USV 和UUV 在第k个航迹点处的转弯角分别为 γAk, γSk, γUk,其计算方法同式(23),航迹处转弯角惩罚函数的计算如式(52)所示。
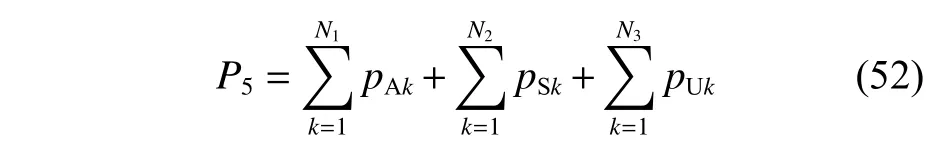
2.3 基于差分进化算法的求解方法
在上述约束条件下,UAV,USV 和UUV 三者的时间协同航迹规划问题可以转化为优化问题,如式(53)所示。
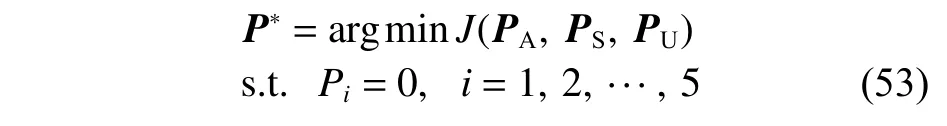
式中,P*为 使J(PA,PS,PU)最小的航迹合集。为了方便寻优计算,将约束条件,如禁入禁出区约束、威胁区约束、爬升和下降角约束、转弯角约束及时间协同约束转化为惩罚项,如式(54)所示。对应的适应度函数如式(55)所示。
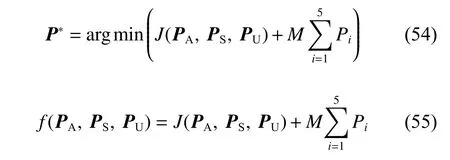
式中:M为惩罚系数,是一个很大的正数项。当所有约束均得到满足时,式(54)中的惩罚值为0,惩罚值为不满足约束个数的整数倍;M值的设定应大于优化项的值; 优化项的所有系数之和为1,各优化项系数的值根据其的权重而定。在此设计下,权重大的优化项会被着重考虑。此优化项系数的设定使代价函数保持了一定的梯度。在整个寻优过程中,满足更多约束且优化项的值越小的个体会被保留,从而产生更多可行的解。
通过分析,无人平台的航迹点数量较多,约束较为复杂,优化目标带有梯度性,是一个维度较高的非线性优化问题。因为DE 算法在求解维度较高的非线性优化问题方面具有独特的优势,所以本文采用该算法进行求解。DE 算法是一种基于种群差异的进化算法,其利用群体内个体之间的合作与竞争产生的集群智能模式来指导优化搜索。DE 算法特有的进化操作使该算法具有较强的全局收敛能力和鲁棒性,非常适合求解一些复杂环境下的优化问题。基于DE 算法的路径规划流程如图5 所示(图中 ,Gen为代数),具体步骤如下。
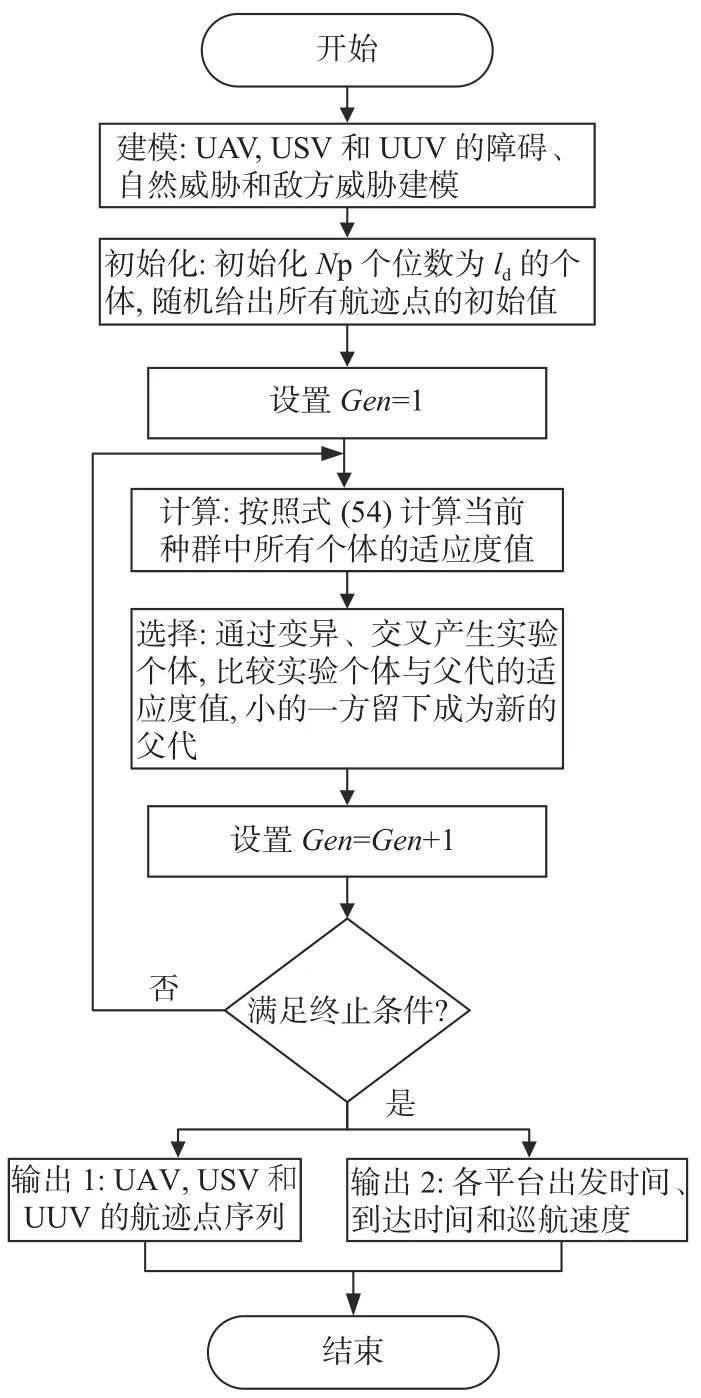
图5 基于差分进化算法的路径规划流程图Fig. 5 Flowchart of path planning based on DE algorithm
步骤1:对航迹点进行编码。前文采用等分方法确定了航迹点的x轴坐标,UAV 在空域内运动,USV 在水面运动,UUV 在指定深度的水下运动,种群中的个体包含这3 个无人平台剩余的需要确定的坐标信息。UAV 的航迹点数量为N1,变量个数为 2N1; USV 的航迹点数量为N2,变量个数为N2; UUV 的航迹点数量为N3, 变量个数为N3。按照UAV,USV 和UUV 的顺序给个体进行编码,编码的总长度D为三者路径变量个数的总和,如式(56)所示。
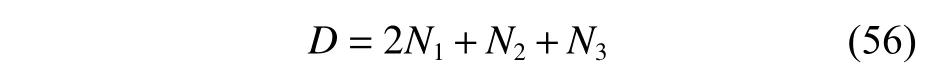
由上式可知,航迹点数量越多,编码长度越长,解空间会越大,求解的时间也就越长。因此,需要根据环境的复杂程度来确定航迹点的数量。若环境简单,可适当减少航迹点数量,则求解时间会变短;若环境复杂,为了避开不可行区域,需要适当增加航迹点数量,则搜索到更优解的可能性会更大。

步骤3:计算适应度函数。对种群个体内的航迹点坐标进行解码后,可分别得到UAV,USV和UUV 的航迹点序列WPA,WPS和WPU,将其带入航迹代价函中,即可得到每条航迹的代价值。
步骤 4:变异、交叉和选择操作。首先,对每个个体进行变异操作,得到变异个体;然后,将变异个体与父代进行交叉,得到实验个体;最后,将实验个体包含的航迹点序列代入适应度函数进行计算,并与对应的父代个体进比较,适应值小的一方保留下来作为新的父代。
在优化初期,主要是寻找航迹规划的可行解,因此需要增加种群的多样性,防止过早陷入局部最优。在优化后期,主要是从可行航迹中寻找出最优航迹,需要设置较小的变异算子,不断逼近最优解。但变异算子是影响种群多样性的关键控制量,因此,设计自适应变异因子F如下:
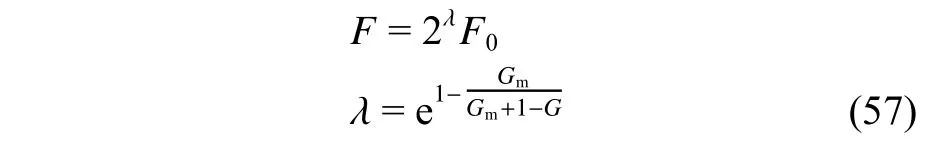
式中:F0为 常数变异算子;Gm为最大迭代次数;G为当前进化代数; λ 为随G自适应变化的参数。
3 仿真实验
本文海上无人系统的平台仿真分析包括1 架UAV、1 艘USV 和1 艘UUV,因各无人平台从不同的起点出发,故按照各平台与目标点的距离,将空间划分为近、中、远3 个区域,即区域1、区域2 和区域3。为了确定这3 个区域内最优的航迹点数量,设计了航迹点数量对比实验,并将航迹规划成功率作为指标。为了验证目标函数的合理性,在复杂环境下使用DE 算法求解其有效性。以27 组起点组合作为算例,每个算例独立进行50 次蒙特卡罗方法实验,记录规划成功率。而为了验证所提时间协同策略的有效性,经对仿真结果的分析,求解出了出发时间间隔和巡航速度。此外,仿真计算使用的是一台CPU 主频为3.6 GHz 和RAM 空间为16 GB 的电脑。
3.1 环境及初始条件设置
设计的实验场景包括3 个地理围栏,7 个禁入区(包括海底地形1 个),9 个威胁源(空中、海面和水下各3 个)。威胁源的信息如表1 所示,其中对空雷达威胁、海面雷达威胁和水下声呐威胁的系数分别对应LATi,LSTi和LUTi。空中禁入区的信息如表2 所示,地理围栏的信息如表3 所示,海面禁入区的信息如表4 所示。
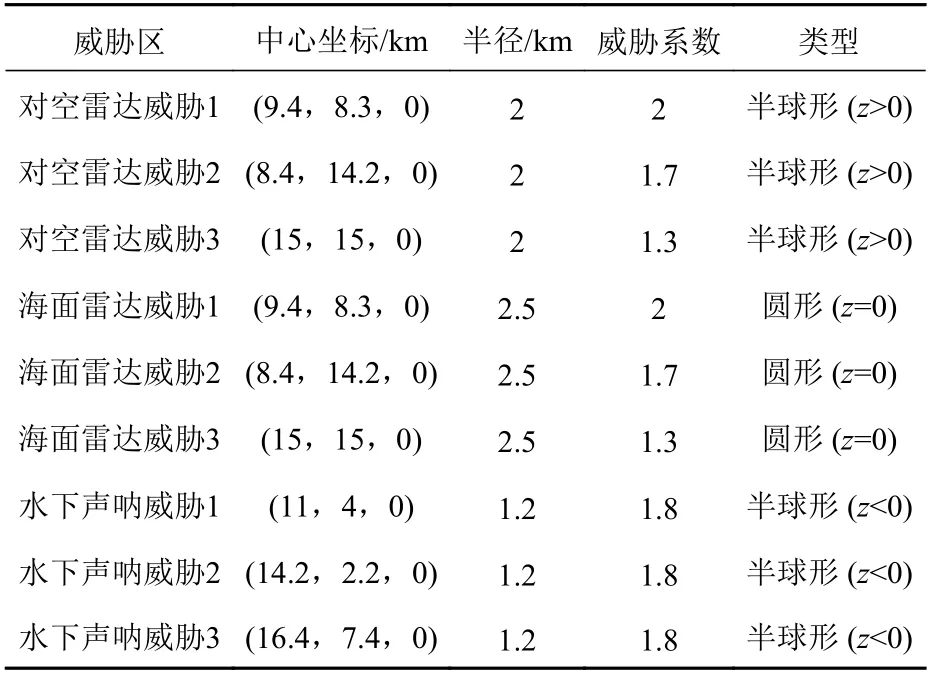
表1 威胁源信息Table 1 Information of threat sources

表2 空中禁入区信息Table 2 Information of forbidden zones in the air
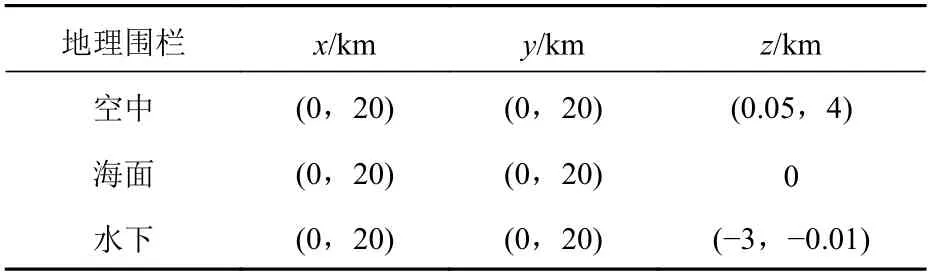
表3 地理围栏信息Table 3 Information of geofence
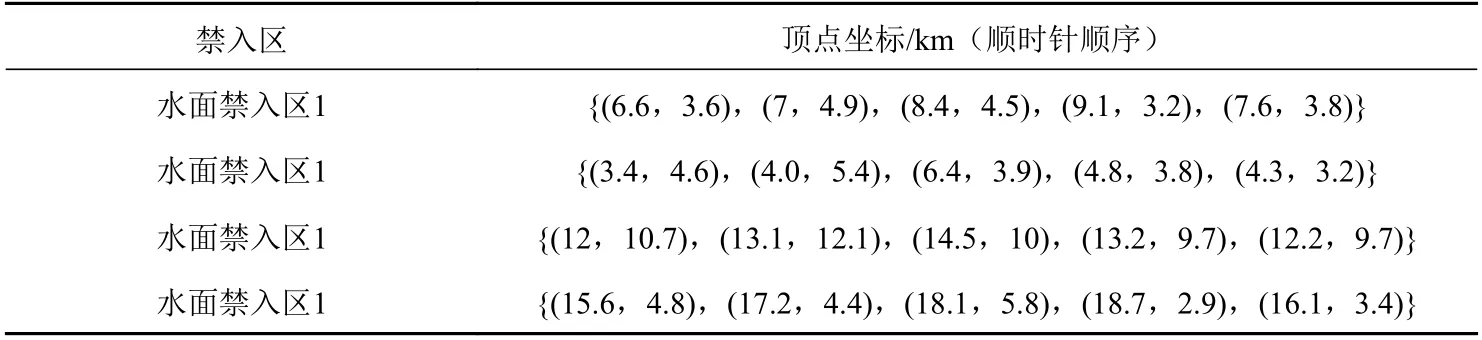
表4 海面禁入区信息Table 4 Information of forbidden zones on the sea surface
各无人平台的航迹信息和运动性能信息如表5所示,划分的3 个区域如图6 所示。以图6 中红色三角形所在区域为例,由于UAV 和USV 存在转弯约束,自然环境和敌方威胁区的分布导致从红色区域出发到目标点不存在满足所有约束的可行航迹。因此,除了无可行解的区域,在其他区域内为3 个平台分别选定1 个起点,每个平台就有3 个起点,并按照所在区域编号,分别命名为起点1、起点2 和起点3。所有起点的坐标均在图6 中详细标识。为方便记录,3 个平台的起点的组合编号规则如下:按照UAV,USV 和UUV 的顺序,将各自起点的数字作为编号的组成,以UAV 起点1,USV 起点2 和UUV 起点3 为例,该起点的组合编号就为123。按照此编号规则,可产生27 种编号组合。UAV 在三维空间飞行,航迹存在爬升段、平飞段和下降段,因此需要至少2 个航迹点。根据前期的仿真实验,发现航迹点数量的设置与航迹规划的成功率具有一定的关系。以区域1 为例,增加航迹点会增大搜索空间,需更多的时间来完成搜索,而航迹点个数的增加也会导致航迹点密度的增加,致使爬升和下降角约束更不容易得到满足,航迹规划的成功率反而会减低。因此,将起点在区域1、区域2 和区域3的航迹点数量范围设定为2~3。UAV 可以在500~2 000 m 高度范围的空域飞行,USV 在海平面飞行,UUV 在水下指定深度航行。3 个平台的起点虽不同,但终点一致。

图6 海上无人系统航迹规划起点分布Fig. 6 Starting points of UMS path planning

表5 UAV, USV 和UUV 初始状态信息Table 5 Initial status information of UAV, USV and UUV
航迹规划求解用到的DE 算法的参数设定如表6 所示。
优化函数式中的主要参数设定如表7 所示。表中,A1,A2,A3和M分别为航程优化项、爬升和下降角优化项、转弯角累计优化项和惩罚项系数。
3.2 仿真结果分析
3.2.1 最优航迹点数量
航迹点数量与航迹规划的成功率有一定的关系,为确定起点在区域1、区域2 和区域3 内的最优航迹点数量,设计了蒙特卡罗实验。使用起点组合111,222 和333,分别以航迹点数量2 和3 独立进行50 次蒙特卡罗实验,DE 算法的参数设置如表6 和表7 所示。选择适应度函数小于100 作为规划成功的判别条件。规划的航迹满足所有约束条件,适应度函数小于100。

表6 差分进化算法的参数设定Table 6 Parameter setting of DE algorithm

表7 优化函数的参数设定Table 7 Parameter setting of optimization function
最优航迹点数量的仿真结果如图7 所示。图中,横轴数字由起点编组号和对应实验使用的航迹点数量构成,例如111-2 表示起点组合号为111,航迹规划时航迹点数量为2;纵轴为航迹规划成功率的百分比。从图中可以看到,111-3 的航迹规划成功率最低,111-2 的航迹规划成功率为74%,因而起点在区域1 内的航迹规划适宜采用2 个航迹点。而在区域2 和区域3 中,采用2 个航迹点的航迹规划成功率均比采用3 个航迹点的航迹规划成功率低。在仿真环境中,从区域2 和区域3 中出发前往目标点需要面临更多的障碍和威胁,增加航迹点可以提高航迹规划的成功率。因此,对于起点在区域1 内的航迹规划适宜采用2 个航迹点,而在区域2 和区域3 中的适宜采用3 个航迹点。
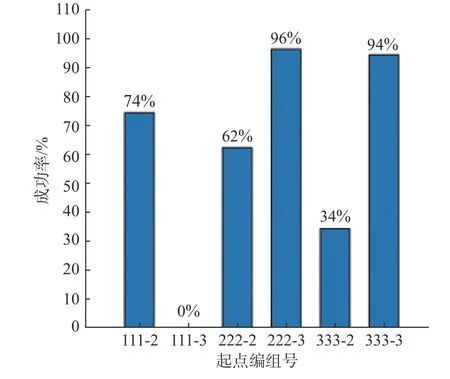
图7 最优航迹点数量Fig. 7 Numbers of optimal waypoints
为进一步说明航迹点数量对于采用DE 算法求解航迹成功率的影响,选取起点编组号333 进行仿真实验。UAV,USV 和UUV 航迹的航迹点数量均为N(N=1,2,···,6),为方便记录,取编号为333-1,333-2,333-3,333-4,333-5 和333-6。算法和目标函数参数设定分别如表6 和表7 所示,其中基因长度D=4·N。每组独立进行50 次蒙特卡罗实验。选择适应度函数小于100作为判别规划成功的条件。仿真结果如图8 所示。由图可见,当航迹点数量小于3 和大于4 时,航迹规划成功率较低;当航迹点数量为3 或4 时,航迹规划成功率较高。当航迹点数量小于3 时,规划的航迹容易穿越威胁区或是不可行区,当航迹点数量大于4 时,搜索空间维度增加,在该种群规模和设定迭代次数下,优化算法难以搜索出可行航迹。
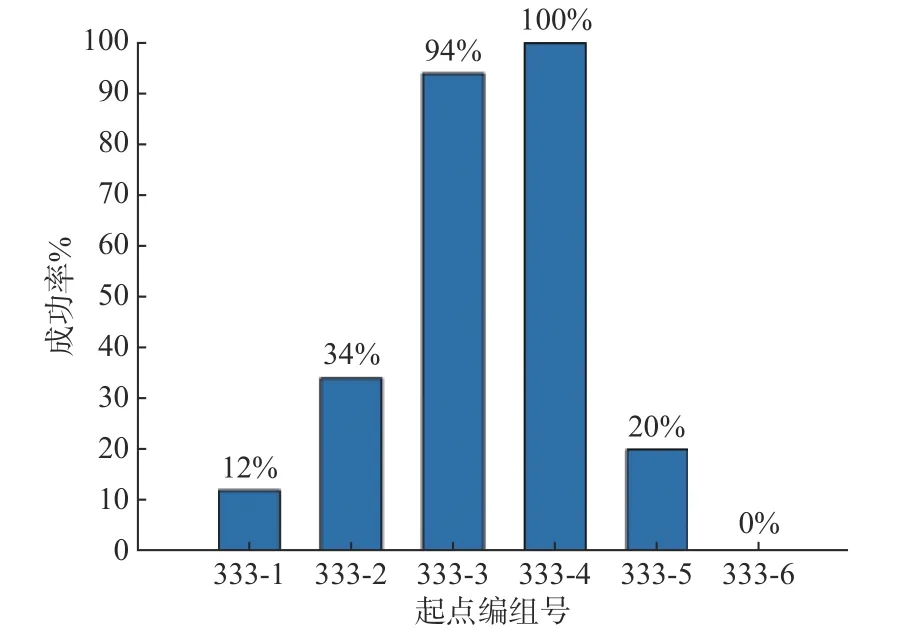
图8 航迹点数量对航迹规划的影响Fig. 8 Influence of waypoint numbers on path planning
另外,当航迹点数量大于4 时,适当增加种群规模和迭代次数,可有效提高航迹规划成功率,但单次规划的时间也会相应增加。当设定种群规模为240,最大迭代次数为300,航迹点数量为5,其他参数不变时,规划成功率可以达到100%。表8 所示为与图8 中的起点编组号333-4 的结果对比。可见,当航迹点数量为5 时,同样的规划成功率下单次规划耗时90.255 s,而当航迹点数量为4 时,单次规划耗时仅需25.777 s。

表8 单次优化耗费时间对比Table 8 Time consumption comparison of single optimization
3.2.2 优化函数和差分进化算法适应性
为了验证目标函数的合理性和DE 算法的适用性,将生成的27 个起点编组作为27 个算例进行了航迹规划实验,编组结果如表9 所示。根据最优航迹点数量仿真结果,选取起点在区域1 中的2 个航迹点,在区域2 和区域3 中的3 个航迹点,对每个算例执行50 次蒙特卡罗实验,并记录规划成功率。将适应度函数小于100 作为规划成功的判别条件。表9 所示的仿真结果显示,规划的航迹满足所有约束条件。

表9 27 组实验规划结果Table 9 Planning results of 27 groups of experiments
UAV 的起点在区域2 和区域3 中时其整体航迹规划成功率在78%~100%之间,且规划成功率为100%占比为77.8%。而当UAV 的起点在区域1 中时,整体的航迹规划成功率在54%~74%之间,规划成功率较低。由于区域1 内的距离小,航迹点密度较大,UAV 的航迹在爬升和下降角上不易满足约束,因此此类起点编组的规划成功率会较低。其原因在于,USV 和UUV 航迹点的坐标维度相比UAV 少一维,受到的约束会更少,起点分布对其航迹规划成功率的影响也较低。整体上,27 个 算 例 的 求 解 时 间 在17.856~23.154 s 之间,适用于离线规划。
3.2.3 时间协同策略及航迹分析
由起点组合332 解算得到的航迹如图9 所示,其从不同角度对航迹结果进行了展示。图9中包含了所有禁出区、禁入区和威胁区,其中禁入区和威胁区在原来形状的基础上进行了膨胀处理。图9 中:红色的框为空中禁出区,绿白相间的2 个圆柱体用于模拟风暴区,3 个表面朝z轴正方向的半圆表示雷达威胁区;位于xoy平面的深红色方框为USV 的禁出区,该平面上3 个黑色的圆表示雷达对水面的探测区,4 个多边形表示水雷区和岛礁区;绿色的长方体框为水下禁出区,浅蓝色的栅格面表示海底起伏的地形,3 个表面朝z轴负方向的半圆表示声呐威胁区。
UAV 在500~4 000 m 范围内运动,空中的红色线条为UAV 的航迹。USV 在海平面上运动,水面亮蓝色的线条为USV 的航迹。UUV 在深500 m的水层运动,水下黑色的线条为UUV 的航迹。在同时到达目标点的前提下,为尽可能缩短距离,由图9 可以看到UAV 和USV 的航迹紧贴禁入区和威胁区的边缘。虽然规划出的航迹距离禁入区和威胁区很近,但因此前对该类区域进行了膨胀处理,故规划出的航迹满足安全距离。
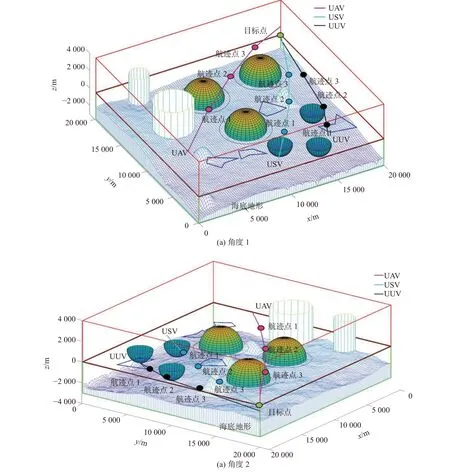
图9 海上无人系统航迹规划结果Fig. 9 Results of path planning of UMS
为同时到达目标点,首先计算UAV,USV 和UUV 到达目标点的时间区间,然后按照提出的时间协同策略计算各平台的出发时间和巡航速度。如图10 所示,各个色块代表对应平台到达目标的时间区间,色块的上、下边分别代表到达目标的最大和最小时间。优化开始到第40 代时,在全局范围随机生成航迹,这一阶段主要是使个体更加多样,因时间协同、最大转弯角等5 个约束中有较多的约束没有得到满足,故平台到达目标点的时间区间波动较大。从第40~90 代,时间协同、最大转弯角等其他约束逐渐被满足,时间区间波动放缓。从第90~160 代,搜索出的航迹基本满足约束条件,这一阶段主要是进行优化函数的寻优,随着航程、累计转弯等优化项的进一步优化,各平台到达目标点所需时间逐渐减少。
从图10 还可以看到,优化结束后,UAV 到达目标的时间区间为16.71~38.44 min,USV 到达目标的时间区间为21.78~35.38 min,UUV 到达目标的时间区间为23.40~35.08 min。因此,UUV 以13 m/s的速度最先出发,在UUV 出发1.62 min 后,USV以15 m/s 的速度出发;UUV 出发6.69 min 后,UAV以23 m/s 的速度出发,3 个平台同时到达目标的最短时间应该为UUV 出发后第23.4 min。
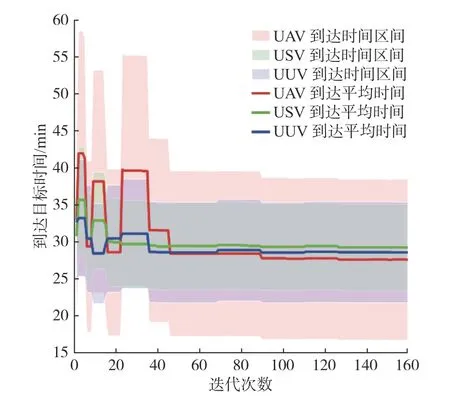
图10 海上无人系统抵达目标点的时间区间Fig. 10 Time interval of UMS for reaching the target point
航迹的优化目标函数随迭代次数的变化曲线如图11 所示。由图可以看出,在优化初期,惩罚函数使得随机生成航迹的函数值比较高,这一阶段主要是使个体更加多样,规划的航迹满足了时间协同、最大转弯角等5 个约束中较少的约束条件。从第10~70 代,采用差分进化算法主要寻找满足所有约束条件的可行解,此时,函数值降低至100 以下。所产生的航迹满足约束条件,验证了前文所设计惩罚函数的合理性。从第91 代以后,主要是寻找使优化函数值最小的解,适应度函数值收敛至16.85。

图11 航迹优化目标函数值优化过程Fig. 11 Optimization process of path optimization function
4 结 语
本文提出了基于DE 算法的海上无人系统时间协同航迹规划方法,实现了多约束条件下的航迹规划,在复杂的障碍环境下实现了海上无人系统的精准时空协同,具有一定的应用价值。首先,采用地理围栏的检测方法将障碍和威胁规避问题建模为多约束条件,使用惩罚函数将航迹规划问题转化为无约束的优化问题。然后,运用DE 算法进行优化求解,其优势在于能够保持搜索初期的多样性和后期的精确性,保证最优航迹的求解。然而,随着航迹点个数的增加,求解时间也不断增加。受求解时效性的限制,本文所提方法只能应用于离线航迹规划,后续还将针对更大规模的海上无人集群的离线规划展开更深入的研究。
