基于TDoA网格邻域匹配的飞机多点定位新方法
2022-09-06戴敏
戴 敏
(中国民用航空飞行学院计算机学院 四川 广汉 618307)
0 引 言
随着航空交通的持续发展,空中交通管制(Air Traffic Control,ATC)需要管理的飞机数量也日趋增加。目前,大型机场的每天起降量超过1 500架次。空中交通管制的关键是需要知道飞机在任何时刻的位置。对于地面管制员,获得飞机位置的传统手段包括高频语音通信和一次/二次监视雷达(PSR/SSR)[1-2]。近些年,随着技术发展和更严格的定位要求催生了其他飞机定位方法,主要有广播式自动相关监视协议(ADS-B)和多点定位(Multi-lateration,MLAT)[3-4]。其中,ADS-B完全依赖于飞机向其他飞机或地面站正确广播自己的位置,而MLAT则利用多个不同地面站接收到信号的到达时差(Time Difference of Arrival,TDoA)进行独立定位[5-6]。与以往的雷达监视相比,这两种定位方法都有效提高了定位精度,其中MLAT的定位独立性更强,是未来空中交通管制发展的关键技术。
MLAT方法主要是利用TDoA进行定位,TDoA测量的准确性直接影响定位精度,其中误差源主要有无线电非视距(NLoS)传播中的多径效应以及测量系统误差,另外,地面接收站的几何部署结构也影响着定位精度。目前,一些学者对MLAT方法进行了改进,改进主要有两个方向:对MLAT中位置求解过程的改进[7-8]和对TDoA数据的后处理[9]。文献[7]对MLAT中基于TDoA获得的定位方程组的求解过程进行改进,融入了Bancroft算法使获得的解更准确。文献[8]在用于机场地面监视的MLAT模型中,将TDoA数据建模为统计模型,然后使用最小二乘法或奇异值分解等方法对这个模型进行求解,从而获得飞机位置估计。文献[9]采用Kalman滤波中递推估计思想对TDoA进行处理,以此减小噪声干扰产生的误差。在上述改进方案中,定位精度仍然不够理想,有些方法利用复杂的误差估计算法来提高TDoA测量准确性,运算量很大会影响定位效率。
当前MLAT以及一些改进方法都是通过测量TDoA和距离计算来定位,这样不可避免地受到地面站分布和TDoA测量过程中各种干扰的直接影响。本文彻底改变了这一做法,不用直接根据TDoA计算距离来定位,而是将测量到的TDoA与预期TDoA进行匹配来定位。该方法的具体思想是:首先将监测空域进行网格分割,计算各网格中心点到各地面接收站的预期TDoA。然后,在实际定位中,根据测量到的TDoA向量,通过提出的加权K-最邻近(K-Nearest Neighbor,K-NN)算法将测量TDoA值与预期TDoA值进行匹配,通过邻居加权平均来估计最终的飞机位置。这种方法有以下几个优点:
(1) 提出一种新的定位技术思想,通过反向推理来进行定位,对扩展定位技术路线具有一定的意义。
(2) 对传统K-NN进行改进,构建加权K-NN算法,使其在飞机定位应用中具有更高的精度。另外由于采用了邻域计算,所以在噪声环境下具有较强的鲁棒性。
(3) 由于该方法不是直接根据接收站测量的TDoA进行几何运算定位,所以对地面接收站的几何结构依赖性较小。
在一个真实数据集上评估了本文方法,结果表明在广域环境下的定位性能优于MLAT,特别是存在较大噪声的情况下。另外,本文方法可扩展性更强,可以提高监视范围,且不依赖于完美的接收站几何部署结构。
1 飞机定位问题
飞机定位问题与其他无线定位问题有以下几点区别:(1) 室外环境,与许多定位问题不同,飞机定位问题是室外的,为此需要为信号损失和传播构建一个户外传播模型。(2) 远距离,在广域空中交通管制监视中,覆盖的距离远大于局部或室内问题。对于巡航高度飞行的飞机(商用飞机通常为1万米或更高),需要观测400 km或更远的范围。
目前实际应用的空中交通管制技术之一是ADS-B协议,其使用两个潜在的数据链路(1090ES或UAT),飞机自动将其位置和速度信息(每秒2次)以及其标识(每5秒1次)广播给附近的其他飞机和地面站。由于可以用廉价的无线接收器捕获无线信号,众包传感器网络近年来也越来越受欢迎。为此,使用无线接收器就可以接收飞机发送的任何信号(包括ADS-B和SSR),只需要获得这些信号的接收时间差就可以进行定位,因此出现了MLAT定位方法[10]。
2 MLAT及缺陷分析
2.1 MLAT定位方法
MLAT根据飞机发送信号的TDoA来计算之间距离,然后再根据多个接收站之间的位置关系来定位飞机的位置[11]。
为了使用MLAT定位目标的二维坐标,需要测量至少三个接收站从某个飞机接收相同信息的时间。通过一个TDoA信息所获得目标的位置轨迹为一个双曲线,当存在2个TDoA信息时,两条曲线的交点即为目标的平面二维坐标[12],如图1所示。中央处理站根据接收站之间信号的TDoA,通过相交双曲面计算来获得飞机位置。当设定目标位置为三维坐标时,则至少需要4个接收站。
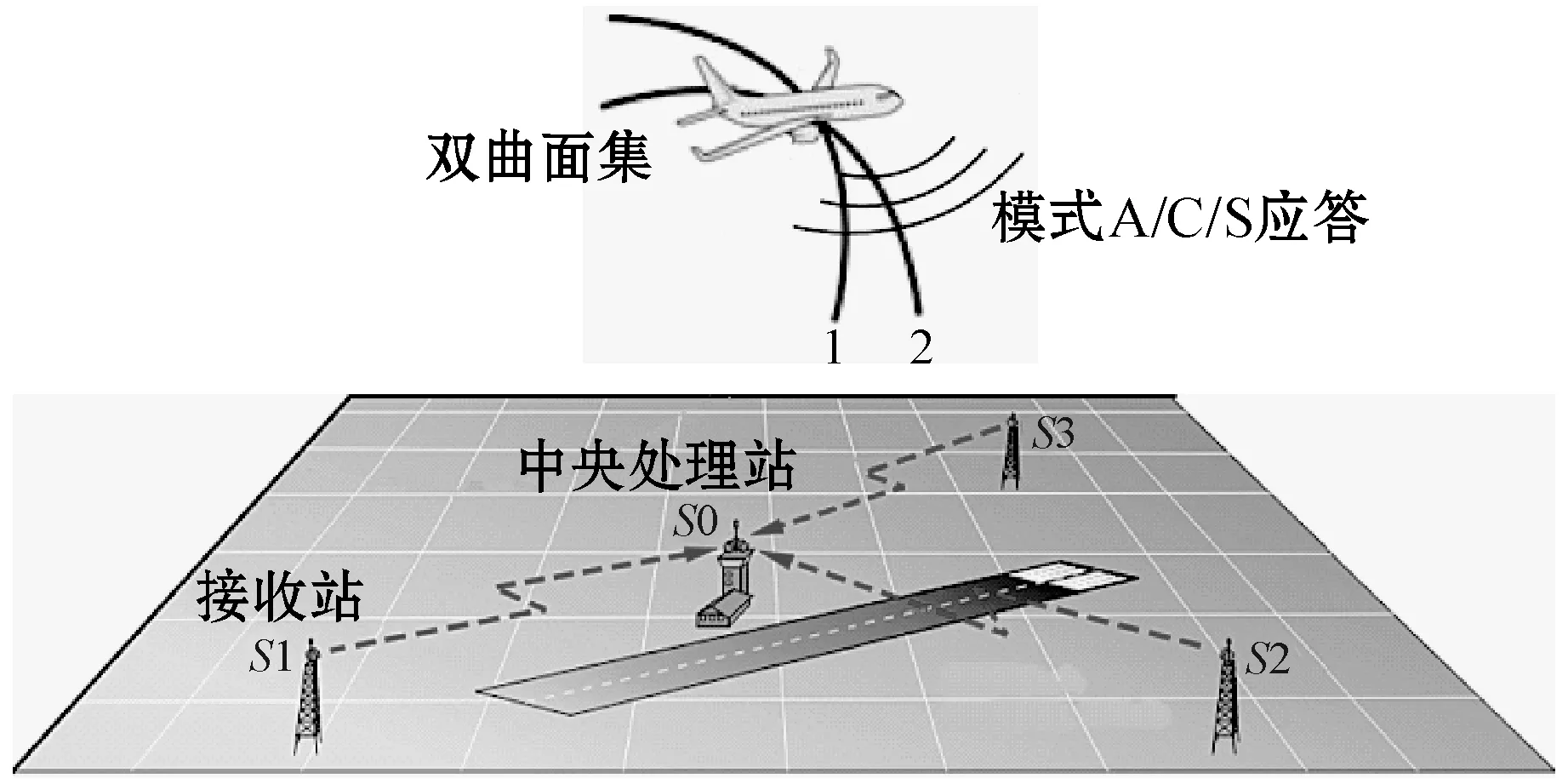
图1 具有三个接收器和两个双曲面的基本MLAT结构
假设有M个接收站捕获到飞机信息,(x,y)为飞机位置二维坐标,(sxi,syi)为接收站i的位置,那么飞机与接收站i的实际距离为:
(1)
定义飞机到接收站i与到基准接收站1的距离之差的实际值为ri,1,表示为:
(2)
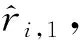
(3)
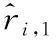
(4)
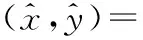
(5)
式中:向量R=[r2,r3,…,rM]T,R1=[r1,r1,…,r1]T,E=[e2,1,e3,1,…,eM,1]T,ei,1=eni,1+eτi,1。ΔR表示为:
ΔR=R-R1+c·E=
[r2-r1,r3-r1,…,rM-r1]T+c·E
(6)
求解式(5)所示的最小化问题有解析表达式方法和迭代方法,其中常用的解析表达式方法为Chan等[13]提出的算法,该算法计算量小且定位精度较高。
2.2 MLAT存在的问题
尽管MLAT很有效,但它仍存在一些缺陷,描述如下:
(1) MLAT非常容易受到系统噪声和异常值的影响。由于存在多径效应和测量系统偏差,测量得到的TDoA中存在随机波动(噪声),这就导致直接根据TDoA计算得到的轨迹曲面存在误差,限制了定位精度。
(2) MLAT定位精度还受到几何精度稀释因子(GDOP)的影响。GDOP是由目标与地面接收站的位置关系决定[14]。在接收站具有相同时间误差下,不同的布局会导致不同的GDOP。由于MLAT要求至少有三个接收站,而地理上的障碍(如山脉、河流)使在服务空域内安装一个通过精心规划几何结构的广域系统更加困难,否则不能提供足够好的GDOP值来实现高服务质量。
图2举例描述了存在两个接收器的部署对目标位置计算误差的影响。其中,圆环内区域表示各个接收器的距离测量误差,两个接收器测量的交集部分表示目标物体真实位置的可能区域。其中:图2(a)为部署较差时的情况;图2(b)为部署较合理时的情况。可以看到,图2(a)中两个接收器部署较近,存在监测范围重合情况,导致定位误差区间较大,严重影响定位精度。
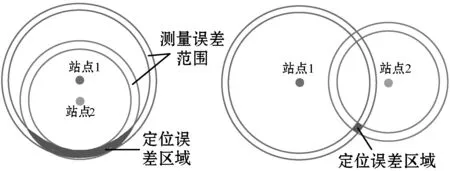
(a) 高精度稀释 (b) 低精度稀释图2 不同部署对几何精度稀释(GDOP)的影响
本文方法对接收站部署几何结构的依赖性降低,可以解决MLAT的可伸缩性和覆盖率问题,特别是在几何结构不理想的情况下。MLAT中,接收站之间的接收范围需要重叠来获得时差,如果接收站部署较近,则会降低总体覆盖率。更糟糕的是,由于GDOP的增加会导致监测准确性迅速恶化。本文方法通过TDoA数据匹配来实现定位,有效降低了受GDOP的影响,且使用较少的接收站就可以达到精确性要求,提高了MLAT的效率。
3 飞机定位方法
如前所述,传统MLAT利用多个接收站捕获信号并计算TDoA来估计目标的位置。本文转变了这个思想,提出一种基于网格匹配的飞机定位方法。不是直接根据TDoA来计算位置,而是将测量得到的TDoA与根据部署结构预先得到的预期TDoA模型进行匹配,从而得到位置。这种方法具有更高的定位精度,且提高了信号利用率和监测部署的总体覆盖率。另外,该方法对接收站部署的几何结构具有很好的适应性,从而可以有效降低成本。
3.1 预期TDoA
本文方法的关键之处在于预期TDoA的使用。首先将监测区域进行预先网格划分。通常情况下,大空域内的飞机定位只需要2维坐标即可,不需要高度信息。为此,为了方便描述,这里将监测空域分割成一个N×M个正方形平面网格,其中:N表示东西方向上网格数量;M表示南北方向上网格数量。如图3所示。
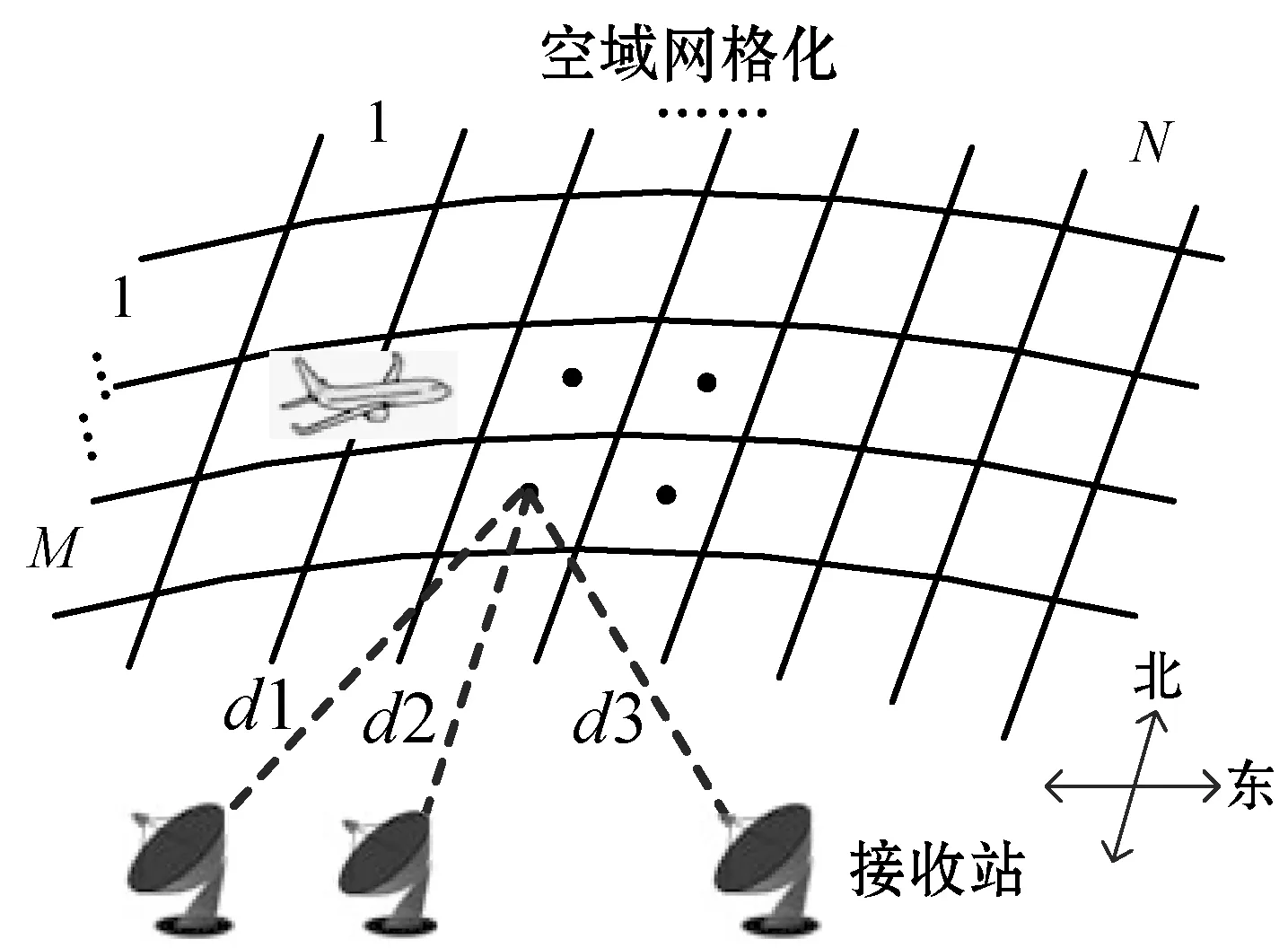
图3 空域网格化及预期TDoA计算
然后,根据已知的接收站部署位置信息,计算每个网格中心到多个接收站(i=1,2,…,n)之间的物理距离(d1,d2,…,dn),然后根据距离计算信号传播时间,以及各接收站之间的预期TDoA向量,这里的接收站数量由接收站的探测范围决定。
设定tmin为某个网格点到多个接收站之间的最小时间,那么将到其他接收站的时间减去tmin可以获得相对于最近接收机的期望TDoA(ETDoA):
ETDoAi=ti-tmin
(7)
3.2 加权K-NN算法
本文方法中,对于测量得到TDoA向量,会利用K-NN算法来将其与预期TDoA向量进行邻域匹配,从而来进行定位。然而,传统K-NN算法在分类应用中对k个邻居采用相同权重[15],这对本文飞机定位的应用不太合适。为此,本文提出一种改进的K-NN算法,称为加权K-NN。也就是在利用邻域网格点位置估计飞机位置时,根据测试点与网格点之间的欧氏距离的高斯函数来分配权重,得到加权坐标,这样有利于提高定位精度。
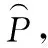
(8)
本文对其进行了改进,利用欧氏距离对参考点坐标进行加权得到测试点坐标(加权K-NN),表示为:
(9)
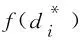
(10)
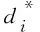
(11)
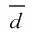
3.3 飞机定位过程
本文首先利用基于地面接收站部署结构计算得到的预期TDoA和K-NN算法来构建位置估计模型。在实际位置估计中,根据测量的TDoA和位置估计模型来估计飞机的位置,具体过程如下所述。
(1) 离线训练阶段。首先将监视区域平面预先分割成一个N×M的网格,对于每个网格的中心,计算该中心到多个接收站之间预期TDoA向量。设定一个新消息被至少3个接收站接收,即至少存在2个TDoA测量数据构成一个子集,然后组合多个数据子集来创建最终训练集。例如,对于5个接收站,总共有16个TDoA子集。最后基于训练集来构建加权K-NN位置估计模型。算法1详细描述了离线训练阶段的过程。
算法1训练阶段
输入:接收站和网格坐标。
输出:根据TDoA训练的估计模型。
1. Input: 网格数据(gridcoords,squaresize), 接收站位置(receiver)。
2. trainingset←[];
%构建训练集
3. grid←constructGrid(gridcoords,squaresize);
%构建网格
4.for∀receiver combinationsdo%训练模型
5. TDoA_training←[];
6.for∀square∈griddo
7. TDoAs←compute TDoAs(receivers.coords,square);
8. TDoAtraining.add(TDoAs,gridsquare);
9.endfor
10. trainingset.add(TDoAtraining,receivercombination);
11.endfor
(2) 在线测试阶段。在测试阶段,接收新消息并计算TDoA测量值。通过加权K-NN位置估计模型,从空域网格中获得与测试数据匹配的k个最近点。算法2描述了测试阶段的过程。匹配过程是根据接收到的物理数据R与预设的网格数据F的欧氏距离进行匹配,表示为:
(12)
算法2测试阶段
输入:位置估计模型,接收消息信息。
输出:位置估计值。
1. Input: 参数k, 消息(flight)。
2.loop
3.m←new position message(flight);
%接收到新消息
4.r←receivers(m);
5.ifnumber of receivers(m)>2then
6. TDoAs←calculate TDoAs(m);
%计算TDoA
7. testset←get testset(r);
%构建TDoA测试向量
8. WK-NN←run WK-NN(testset,k);
%执行加权K-NN
9. estimate←getCenter(WK-NN);
%估计位置
10.endif
11.endloop
很明显,在空域网格中,会有多个邻居网格与实际位置的距离大致相同。因此,k是影响精度的一个重要参数。如果设置k>1,则通过取所有k个邻居位置坐标的加权平均值来估计飞机的最终位置。
图4描述了一个存在4个接收站和3个邻居网格(k=3)时的位置估计案例。其网格中心点位置信息最终的估计位置坐标如表1所示。其中根据4个接收站测量得到的TDoA向量,通过加权K-NN找到了3个最近邻居(N1,N2,N3),然后通过加权平均化得到估计的位置E点,其与实际位置T点最为接近。通过后续的性能评估也表明,邻居位置平均后比任何一个邻居更接近实际位置。
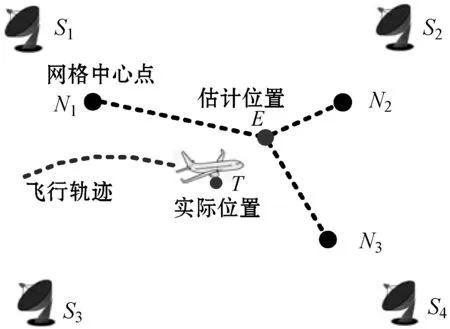
图4 加权K-NN定位案例(k=3)
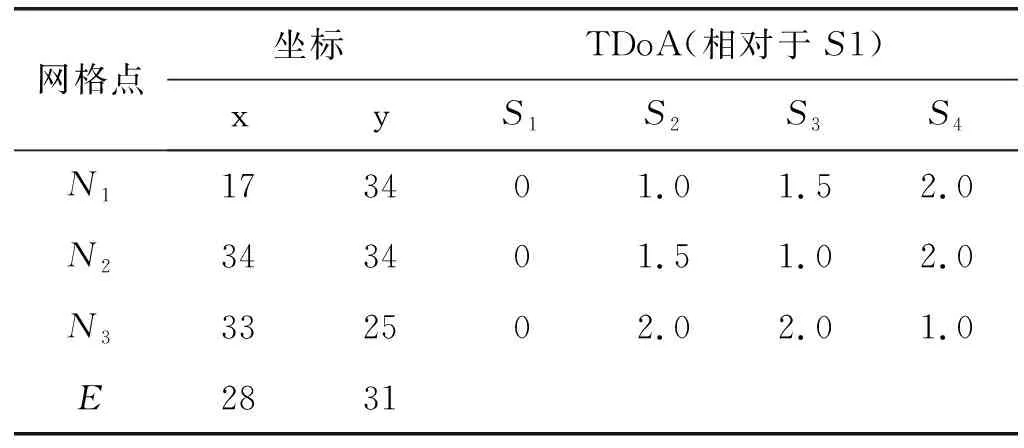
表1 案例中的位置坐标
4 实验与结果分析
4.1 实验设置
由于ADS-B在民航领域已经应用多年,为此有大量真实数据可用作实验数据集。本文从OpenSky网络获得的真实空中交通管制数据。截至目前,OpenSky网络中存在数千亿条空中通信数据,每天捕获超过16 000架飞机的信息。在本文分析中,使用的数据集涵盖2018年6月至2019年6月期间,选择了其中分布较近的5个接收器的数据,共包含超过10万条的ADS-B信息。除了消息内容,主要提取其中的消息接收时间戳,时间戳的时钟分辨率为50 ns。这些信息对应10万个位置,且都能被5个接收站接收,为模型训练和比较分析提供了足够的TDoA数据。另外,这些数据是通过地面接收机SBS-3传感器采集,接收器的监测半径约400 km。
本文在11 500 m的典型飞行高度上构建了一个二维空域,该空域的面积约为150 km×220 km。将该空域进行网格化,构建均匀分布的正方形网格,其中网格数量的确定需要考虑定位效率和定位精度之间折中。另外,所有算法都在MATLAB中实现,运行在配置Intel i5处理器@2.9 GHz/8 GB RAM的PC机上。
4.2 性能评估
为了保证基线定位方法的准确性,通过与飞机ADS-B广播信息的GPS位置数据进行比较,来评估本文方法的定位精度,并与MLAT算法进行了对比。另外,分析了邻居数目和网格尺寸对定位精度的影响。
4.2.1网格尺寸对定位性能的影响
首先,分析网格尺寸对定位精度的影响程度。并在定位误差,对TDoA异常数据的鲁棒性和时间效率方面与MLAT进行比较。设置参数k=5,并构建50 m2到600 m2之间5种不同尺寸的网格并进行实验,统计了定位误差的平均值、中值、均方根误差(RMSE)、定位所需的相对时间,结果如表2所示。
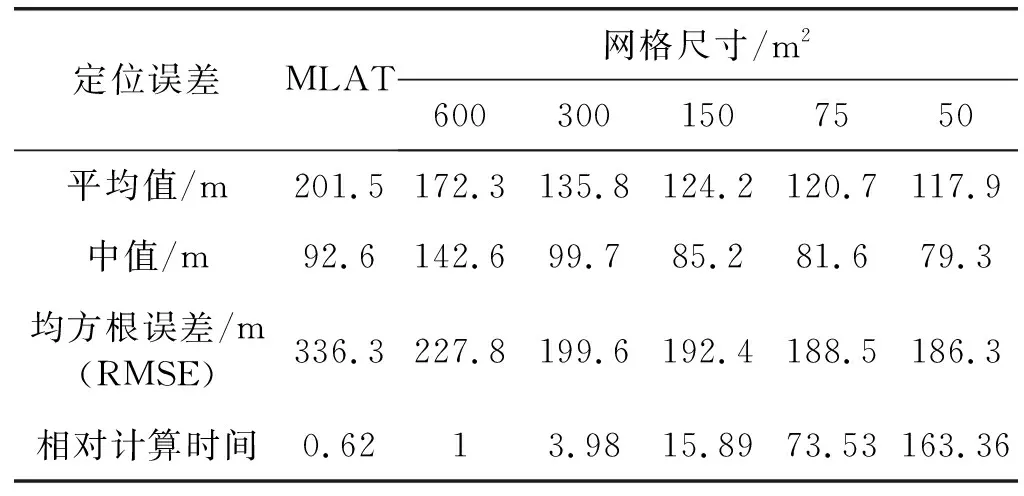
表2 不同网格尺寸下的定位误差(k=5)
对表2所示数据的分析总结如下:
(1) 对于定位误差。缩小网格尺寸、增加网格密度对定位准确性有积极影响。这是因为网格密度越大,算法得到的邻居网格中心就越集中且越接近实际位置,加权后得到的位置估计也就更加准确。例如,网格尺寸从600 m2减少到300 m2时,平均定位误差降低了约21.2%。另外,本文方法的定位精度高于MLAT,当网格尺寸为150 m2时,平均定位误差为124.2 m,比MLAT降低了约38%。
(2) 对于TDoA异常数据。RMSE指标对离群值的敏感度较高,用来评估TDoA测量中的异常点对定位精度的影响。由于数据集是真实数据,其中存在一些测量异常值。通过比较发现,MLAT的误差中值较低,但RMSE很高,说明其对异常点敏感。假设数据集中的平均GDOP为24,而MLAT仅考虑GDOP低于10的“好”数据,这就导致90%以上的消息不可用。而本文方法对精度稀释更具鲁棒性,在更大范围内是有用的。
(3) 对于计算时间。计算时间是准确性和鲁棒性的折中表现。当网格尺寸为600 m2时,本文方法的计算时间可与MLAT相媲美,但会随着空域网格密度的增加而增加。然而,具体计算时间与运行设备相关。在实际应用中,机场的中央处理器通常具有很高的运算效率,即使网格尺寸很小,计算时间也不会造成问题。
由于本文算法的运行平台为个人计算机,在300 m2网格上以小于7 ms的速度计算一个位置。对于实际应用,空域监测的更新率保持小于1 s就能满足要求。因此在空中交通管制监视应用中,本文方法的时间复杂性几乎不会影响监测效果,算法的运行时间不是关键问题。总的来说,本文发现设置网格尺寸小于150 m2时,定位精度不再明显改善,而计算时间还是会成倍增加。因此设置网格尺寸为150 m2时,在定位精度和时间效率之间提供了一个很好的折中。
4.2.2邻居数量对定位性能的影响
下面分析加权K-NN中的邻居数量参数k对定位精度的影响程度,实验结果如图5所示。可以看到,在k小于5时,平均定位误差会随着k的增加而显著改善,特别是对于600 m2大小的网格。当k大于5时,定位误差进一步降低的空间很小,并且对于较小尺寸的网格还会更小。
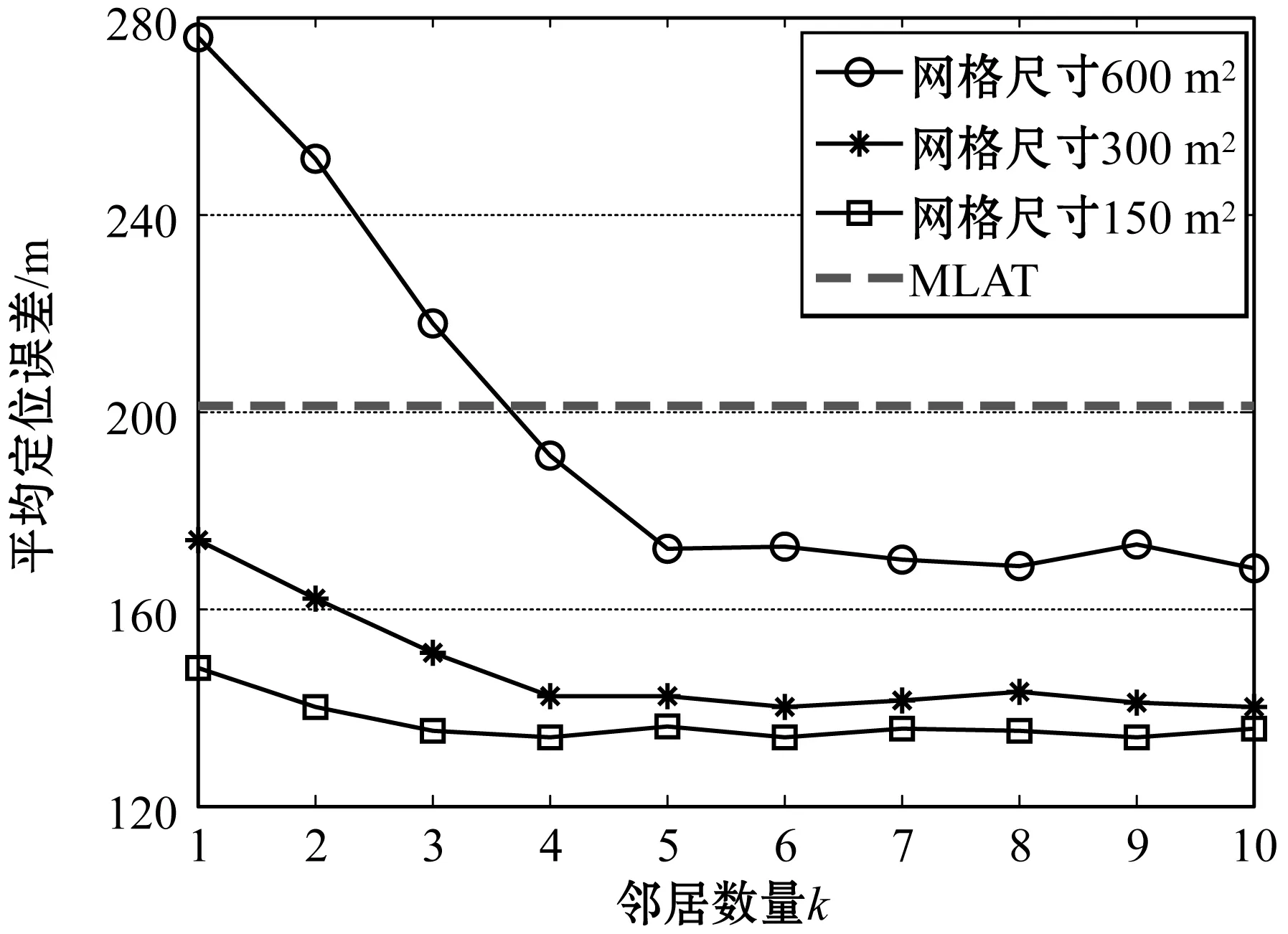
图5 不同邻居数量k和网格尺寸下的定位精度
4.2.3信号噪声对定位性能的影响
与MLAT相比,本文方法的一个主要优点是对噪声的鲁棒性。为了分析TDoA测量中噪声信号的影响,以收集的真实数据为基础进行了模拟测试。在100 km×100 km的空域上构建网格,地面上随机分布5个接收器。对每个网格中心,模拟其发送信号到各个接收站来计算TDoA,并在TDoA中添加表示时间测量误差的高斯白噪声Zi~N(0,σ),其中:0为均值;σ为TDoA噪声的标准差,单位为s。在不同等级的σ下进行实验,并计算定位误差的中值,结果如图6所示。
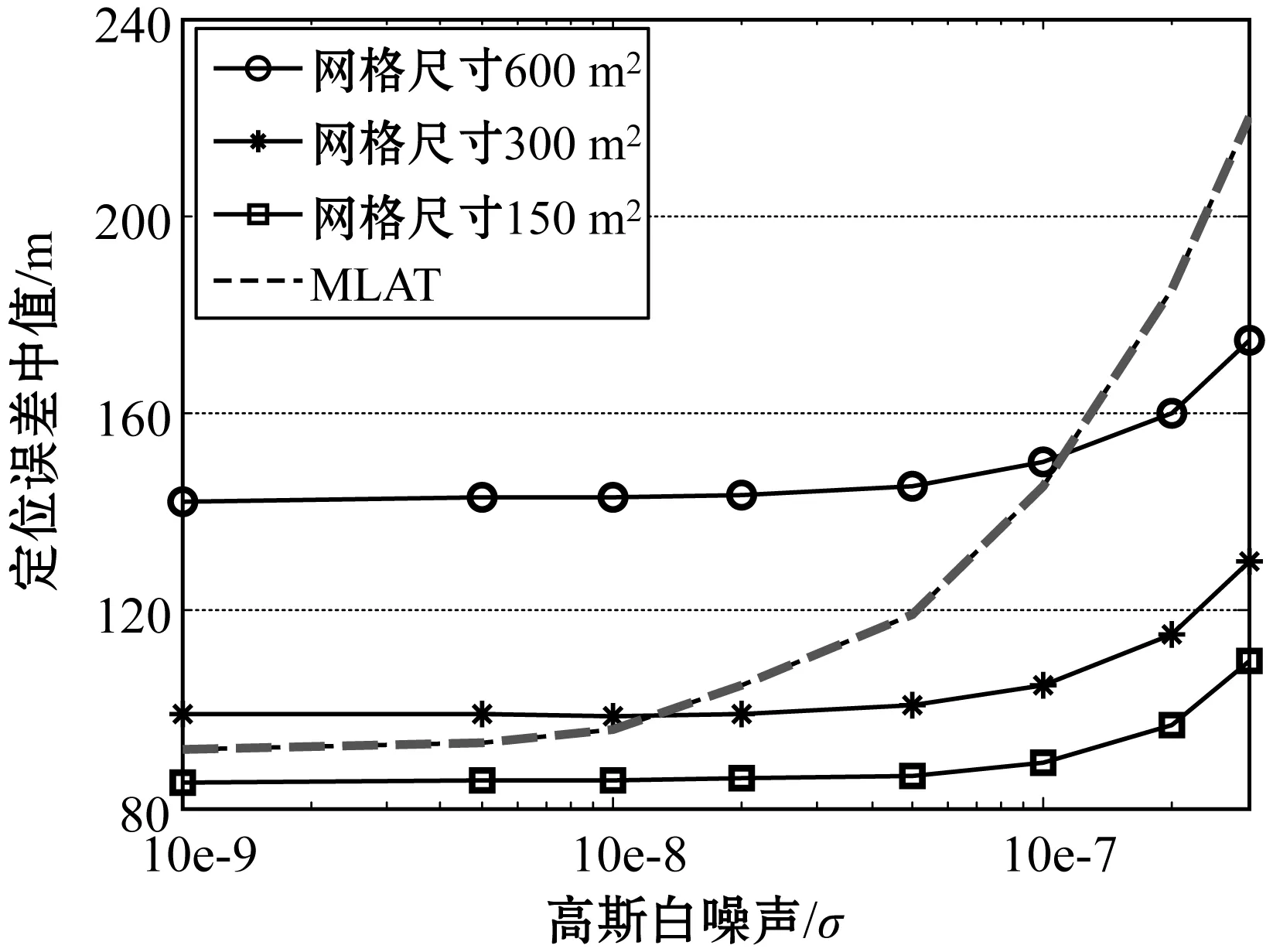
图6 不同噪声水平下的定位误差中值
可以看到,MLAT算法在没有或很少TDoA噪声的情况下性能很好。然而,在噪声水平较高时,MLAT的性能急剧下降。与之相比,本文方法对噪声的鲁棒性要好很多,在噪声水平增加时没有明显恶化。当噪声接近σ=10-7s时,MLAT的定位误差中值达到150 m,超过所有网格尺寸下的本文方法。这是因为MLAT仅在GDOP极低时才表现良好,而本文方法不受此问题的影响。实验发现在MLAT中,只有GDOP小于5的信号才能提供较低的平均定位误差。不幸的是,这样低的精度稀释只存在于很小部分的监视区域。所以在存在噪声情况下,本文方法还具有扩展监视区域的作用。
另外,MLAT算法需要非常准确的时钟同步,并且受到接收器位置几何结构的严重影响。相比之下,本文方法使用低成本的硬件(如SBS-3接收器)也能提供高质量的有效定位。在接收站部署条件有限的情况下,这个特性非常有用。
5 结 语
本文在MLAT的基础上,提出一种逆向匹配的思路来进行飞机定位。通过对空域进行预先网格化,构建预期TDoA数据集,然后利用一种加权K-NN算法来进行邻域匹配,获得最终的飞机位置估计。通过与MLAT方法进行比较,结果表明本文方法明显提高了定位精度,且在存在TDoA噪声情况下同样能实现良好性能。另外,本文方法对地面接收站部署的几何结构要求不高,可以扩展监测覆盖率。
