法向约束的点云数据泊松表面重建算法

鲁猛胜 姚 剑 董赛云

1武汉大学遥感信息工程学院，湖北 武汉，430079

三维点云表面重建是对三维激光扫描仪等测量设备得到的物体表面点云数据进行三维建模的过程，在逆向工程、数字保护、工业检测、增强现实、智慧城市等领域［1-3］，对三维物体表达模型的需求不断增加。由于点云会存在噪声、分布不均匀和局部数据缺失等问题，因此需要恰当的数学模型和高效的算法来提高重建精度和减少运算复杂度。

目前点云表面重建方法主要分为基于计算几何［4］和基于隐函数拟合［5］两种方法，相较前者基于隐函数拟合的方法能对含有噪声的非均匀点云数据进行高鲁棒性的网格化处理。常见的隐函数拟合方法有基于径向基函数［6］、基于符号距离函数［7，8］和基于指示函数［9-11］的表面重建方法。

泊松重建算法是基于指示函数的表面重建方法，它综合了全局和局部拟合的优点，通过局部基函数的层次构造，在整体上进行一致性的误差分配，从而转化为泊松空间问题进行求解。该方法能得到较为平滑的表面模型，对噪声有一定的容忍度，是表面重建领域的主流方法。但由于其依赖于准确的法向，而且未充分利用点云的结构信息，导致重建得到的表面与真实情况有一定的偏离。

本文在屏蔽泊松重建算法的基础上，充分利用法向信息，针对性约束法向不准确的区域，将法向准确度分别定位到屏蔽泊松方程中的采样点权重分配和多重网格求解的八叉树节点扩展中，最终既能保持模型的显著细节，又提高了重建表面的准确度，同时也减少了内存开销。

1 法向约束的屏蔽泊松重建

法向约束的泊松重建算法流程如图1所示。

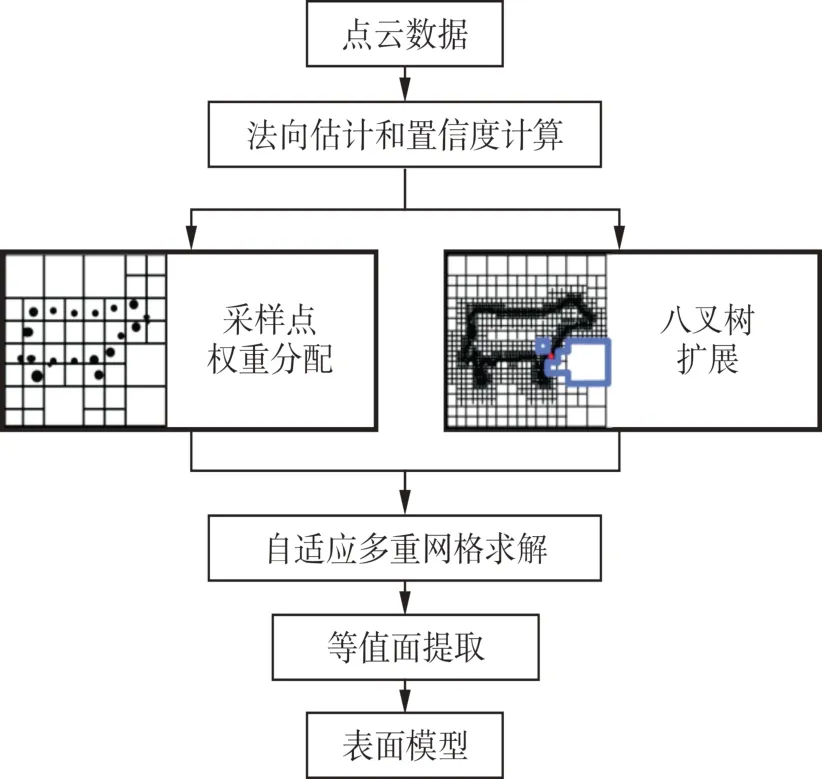
图1 算法流程图Fig.1 Flow Chart of Algorithm

首先针对点云进行法向估计，初始法向通过主成分分析法进行估计，最终法向则通过文献［12］中的自适应邻域法向迭代估计法获取，两者偏差值在高斯分布下的区间置信度即为法向准确度。然后结合法向准确度调整屏蔽泊松方程中的采样点权重，在各个分辨率下均得到更好的位置约束。同时在多重网格求解时，针对性地约束具有不准确法向的点云格网的八叉树扩展。最后求解屏蔽泊松方程，并利用移动立方体算法提取等值面，生成更为贴合的表面模型。

1.1 法向估计和置信度计算

在理想情况下，点云重建表面光滑，可以通过平面来拟合点的局部信息，因此利用主成分分析（principal component analysis，PCA）方法可以准确得到法向n a。给定点云任意一点p，其k邻域点集N b(p)={p1，p2，...，p k}，则根据邻域拟合的平面可以表示为：

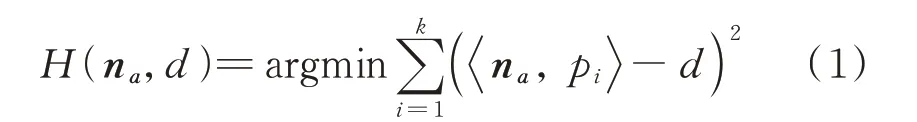
式中，n a为归一化后的拟合平面H的法向量；d表示点p到拟合平面H的距离。通过对式（1）构成的协方差矩阵进行特征值分解，所求取的最小特征值λmin对应的特征向量vmin也就是拟合平面的法向量，即n a=vmin。

利用PCA方法估计的初始法向n a在表面光滑处较准确，而应用到相对锐利区域，邻域特征由于具有各向同性而不显著。按照文献［12］针对尖锐特征的法向估计方法的原理，将其运用到最终法向的估计上，即：

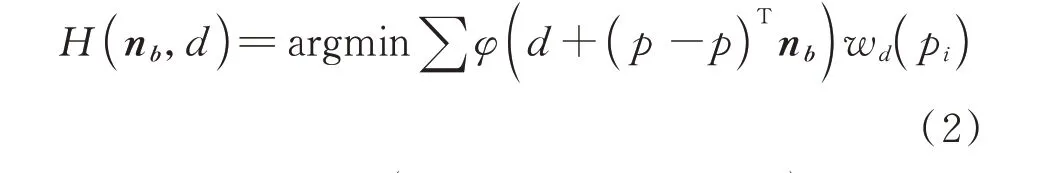
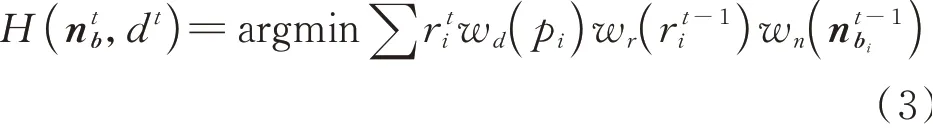
式中，w n(n b)表示法向偏差的高斯权重表示第t次迭代点p i的残差，所求得最小特征值对应的特征向量即为每次迭代的法向。

自适应法向迭代估计的最终法向n b更为精准，点p的初始和最终法向之间的夹角θ可以反应真实模型曲面的曲率，随着θ的增大，拟合表面的法向越来越不稳定，即该区域更有可能是杂乱的表面。通过计算所有点云的θ值得到均值μ和方差σ2，在高斯分布下根据每个样本点所在分布区间，确定每个点最终的置信度αi，即点云的法向准确度。

1.2 法向约束的采样点权重分配

原始泊松重建直接寻求向量场到指示函数梯度场的最佳近似，会导致所求得的表面模型有一个全局性的偏移，而屏蔽泊松算法则通过添加位置约束以使所有采样点的误差得到修正：

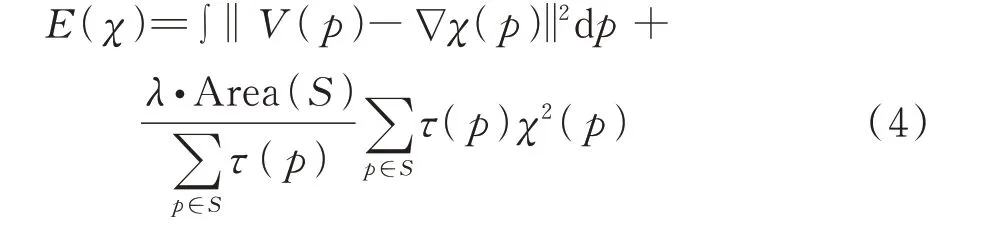
式中，λ为屏蔽因子，权衡梯度约束和位置约束的比重；Area(S)表示采样点附近的重建表面区域；τ(p)表示邻域点的权重，在屏蔽泊松算法中所有样本点的权重都为1。

然而屏蔽泊松算法对所有样本点取相同权重，使法向不准确的样本点也能施加足够的位置约束，从而导致各分辨率下的求解都不精确。如图2所示，在离散化过程中，需要进行由粗到细的求解，对应逐渐加深的八叉树。在每个分辨率下，各网格的估计结果通过计算落入该网格的所有样本点的数量和平均位置得到，即分层聚类。显然当样本点法向不可靠时，引入同样的权重会导致各粒度下的估计结果都存在一定的偏离。因此通过对样本点p i根据法向置信度来分配权重，以求取各粒度下的更为精确的解，即：

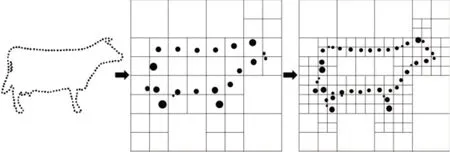
图2 不同分辨率下的权重分配Fig.2 Weight Distribution at Different Resolutions

式中，φ为归一化参数。

1.3 法向约束的八叉树扩展

在屏蔽泊松算法中，给定最大深度D，如图3所示，自适应的八叉树仅在有样本点的区域细分。在进行多重网格求解时，每个深度都有对应的B样条基函数簇，分别对应所在深度的八叉树节点，显然B样条函数并非都能在每一层上完全充满整个函数空间，而且也存在两两非正交，这样父节点的B样条函数不仅仅来自于它的所有子节点，因此需要特别存储上一层的结果。为了解决这一问题，屏蔽泊松算法对原始八叉树进行扩展，即对B样条函数空间进行扩充［14］。如图3（a）所示，对于深度为d的节点，它的上一层d-1中相互非正交的基函数也必须存在，如图3（b）所示，红色点的深度为d，则需要在粗粒度上添加新的八叉树节点，得到图3（c）的结果。

但是假定红色点的法向置信度αi＜δ（δ为阈值），则应该排除对该点处的拟合，即不需要对它所在的八叉树节点进行向上扩展，即得到图3（d）所示的结果，这样既可避免过拟合，又将节省内存开销和运行时间。应当注意到图3（d）中的效果是理想化的，因为该区域的部分八叉树单元可能还受其他样本点的影响而得到扩展，但针对法向置信度小于阈值的若干样本点，仍然能在一定程度上避免全部扩展。

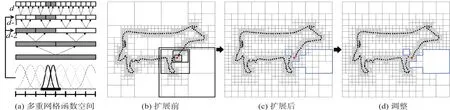
图3多重网格和八叉树扩展Fig.3 Multigrid and Octree Enrichment

2 表面重建结果与分析

2.1 数据集

为了验证算法的适用性和有效性，本文采用具有不同特点的多种数据集进行对比实验，主要包括以下3种：

1）斯坦福三维扫描数据集（以下称Stanford），点云较为均匀，包含Buddha、Lucy和Bunny等；

2）EPFL多视图密集重建数据集（以下称EPFL），其模型存在较多数据缺失，包含Eagle、Monkeys、Paderwski等；

3）文献［13］提供的存在非均匀采样、噪声和误匹配等多种扫描误差的数据集（以下称Berger），主要包含有Daratech、Quasimodo、Dancing Children等模型。

2.2 实验参数和边界条件

本文主要与原始泊松算法和屏蔽泊松算法进行比较，其中参数按照算法作者建议的进行设置，如原始泊松算法屏蔽因子λ=0，屏蔽泊松算法中λ=4等。本文算法参数均与屏蔽泊松算法保持一致，而法向迭代估计具有参数自适应性，法向置信度能适应不同点云数据的法向偏差分布，而针对八叉树扩展的置信度阈值δ也均取最好结果。

狄里克莱条件和诺依曼条件分别是针对边界和边界梯度的约束，而后者在测绘遥感和计算机视觉领域运用更为广泛，因此结合采用的数据集，进行的实验均采用诺依曼边界条件约束［15］，然而应当注意到当存在数据缺失时的情况。图4为EPFL数据集中Eagle模型的结果，图4（b）、4（c）、4（d）的上下子图分别为狄里克莱和诺依曼条件约束，诺依曼边界条件会对该数据缺失区域缺乏限制而生成伪曲面，但本文算法由于针对性约束法向不准确样本点，因而取得了更好的重建效果。

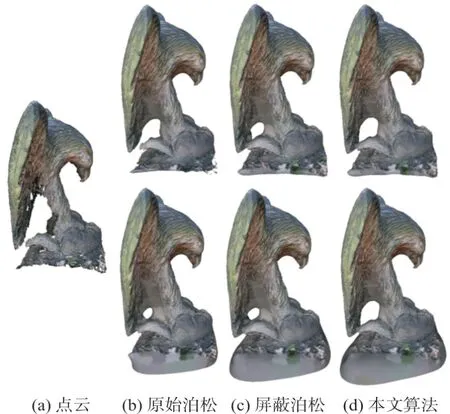
图4 边界条件对比结果图Fig.4 Comparison Result with Different Boundaries

2.3 性能评价指标

本文主要通过两种指标来进行评价：①样本点到重建表面距离的均方根误差（root mean squared error，RMSE）；②重建表面到数据集提供的真实参照表面的豪斯多夫距离（Hausdorff distance，HD）。

2.4 结果与分析

本文的所有实验均在配置为2.3 GHz的四核Intel Core i5 CPU和16GB RAM的计算机上进行，并采用OpenMP进行并行加速处理。

为了评估本文算法的准确性，选取具有不同特点的数据集中的9个模型对本文算法进行了RMSE和HD的准确率对比评价，所有的重建深度均为10，得到如表1所示的结果。其中两种评价指标下的每行数据均通过与最大值作比较而得到归一化处理，值越小表示越准确，最好的结果在表1中通过加粗显示。另外由于EPFL数据集提供的参照重建表面也是通过屏蔽泊松算法获取，因此不进行对照，其HD一栏为空。从表1中可以看到，本文算法在不同类型的数据集上有一定程度的精度提升，其中HD值在Stanford和Berger数据集的5个模型中，均取得了最优结果，而Bunny模型也表现出相近的精度，但本文算法的RMSE值在所有的模型中不甚突出。这是由于屏蔽泊松算法更依赖于位置约束，从而使点云更加贴近生成的表面模型，但由于噪声、数据缺失、误匹配的存在，会导致估计的法向不准确，从而生成的表面在这些区域过度拟合，因此屏蔽泊松算法的HD值相对较高，如图5所示的Dancing Children模型。

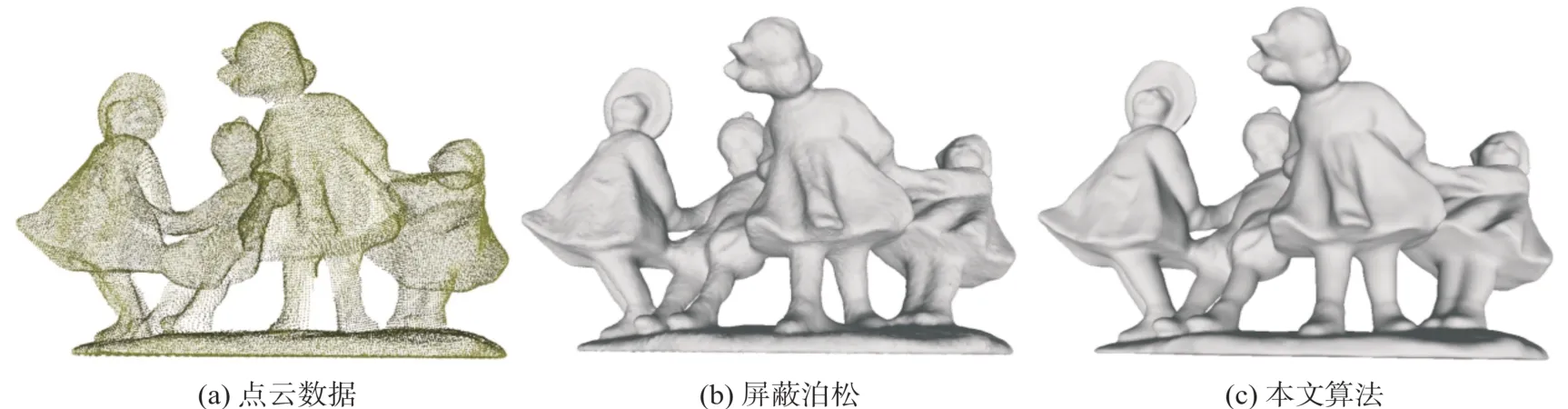
图5 Dancing Children模型的重建结果对比图Fig.5 Comparison Result of Reconstruction Surface on Dancing Children

由表1观察到在EPFL数据集的Eagle、Monkeys和Paderwski这3个模型中，屏蔽泊松算法表现出最差的结果，主要是因为它们均存在着较多的数据缺失（见图4），导致屏蔽泊松算法生成了大量伪曲面。而本文算法则对此进行针对性地约束，根据法向置信度给予权重分配，减弱了边缘噪点的影响，得到更低的RMSE值。

本文算法的运行效率测试对比如表2所示，对Berger数据集中存在较多噪声和数据缺失的Monkeys模型进行实验，重建深度均为11，分别比较了不同置信度阈值参数δ的结果，并与原始泊松和屏蔽泊松算法作对比，与表1中一样，这里RMSE也作了归一化处理。从表2中可以看到，本文算法在不同阈值参数下，其运行时间和内存开销均有一定程度的减少，并随着阈值δ的下降而逐渐降低，可以证明本文算法能有效抑制不准确法向样本点的八叉树扩展，提高运行效率。应当注意到以原始泊松算法作对比，在该模型上屏蔽泊松算法有更多的伪曲面生成，而本文算法的δ的选取也应当考虑准确拟合的效果。

表1 不同数据集模型下的定量对比结果Tab.1 Quantitative Comparison Results Under Different Datasets Models

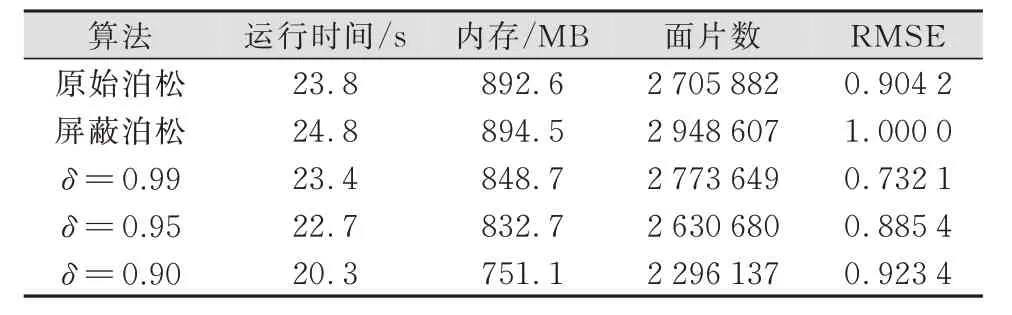
表2 Monkeys模型上的运行效率对比结果Tab.2 Results about Computational Efficiency on Monkeys Model

3 结束语

本文从屏蔽泊松方程在法向不准确区域约束不足的角度出发进行改进，充分利用点云的法向信息针对性约束不准确样本点，通过利用PCA算法和自适应法向迭代估计法确定初始和最终法向，以评价法向置信度，并将该约束分别引入到位置约束的权重分配和多重网格求解时的八叉树扩展中，以减弱或消除不可靠样本点拟合效果。在3种不同特点的数据集上进行的实验结果表明，本文算法在大多数模型上均取得了更精确的重建结果，而且也在一定程度上减少了运行时间和内存开销。