QZSS与GPS重叠频率紧组合相对定位精度分析

罗翠翠 王光盈 叶长斌 景国峰 刘 刚

1山东正元数字城市建设有限公司，山东 烟台，264000

2青岛恒海盛海洋科技有限公司，山东 青岛，266000

准天顶系统（quasi-zenith satallite system，QZSS）是日本新一代区域定位系统，主要在亚太地区提供导航与定位服务［1-3］。QZSS由3颗倾斜地球同步轨道（inclined geosynchronous satellite orbit，IGSO）卫星和1颗中地球轨道（medium earth orbit，MEO）卫星组成，播发L 1、L 2、L 5 3个频率，3个频率与GPS的L 1、L 2、L 5频率相同，与GPS有较好的兼容性［4，5］。

相对定位技术目前主要有两种常用模型：①各系统自己选择参考卫星进行系统内差分即松组合模型；②各系统选择同一个参考卫星进行系统间差分即紧组合模型。松组合模型是相对定位中常用的模型，而随着GNSS（global navigation satellite system）的不断发展，紧组合模型也开始较多地被应用到多系统相对定位中，但需要处理系统间偏差问题［6-8］。吴明魁等［9］对BDS-3试验星/GPS/Galileo短基线紧组合相对定位性能进行了初步评估，发现相同接收机间的系统偏差几乎为0，紧组合相比松组合能有效提高模糊度固定的成功率与可靠性，单频卫星数少的情况下效果更明显；周英东等［10］分析了BDS/Galileo紧组合系统间偏差估计与模糊度固定效果，发现小数ISB（inter-system bias）能进行长期稳定的预报，紧组合相比松组合能有效提高模糊度固定成功率；张小红等［11］评估了BeiDou B2/Galileo E5b短基线紧组合相对定位模型及性能，发现相同类型接收机间系统偏差接近0，不同接收机间系统偏差较大但长期稳定，相较于松组合模型，紧组合模型有效提升了模糊度固定的成功率与可靠性，观测条件较差时效果更为明显。

为进一步分析GPS与QZSS兼容频率间的相对定位精度，考虑到GPS播发L5频率的卫星数较少，本文基于IGS（International GNSS Service）跟踪站构成的短基线，分析了GPS/QZSS组合L 1、L 2、L 1/L 2三种频率紧组合模型相对定位精度。

1 GPS/QZSS紧组合模型

在进行紧组合相对定位数据处理时，要考虑系统间偏差的影响，由于选取组成短基线的两个跟踪站接收机类型相同，相关研究发现相同类型接收机间系统偏差接近0，因此本文在紧组合模型公式推导时不考虑系统偏差的影响。

一般的非差伪距与相位观测方程［12-15］为：

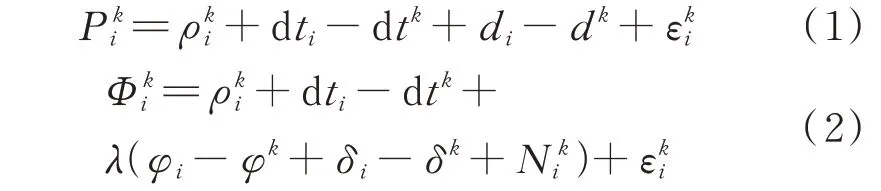
式中，和分别表示载波观测和伪距观测值表示测站与卫星间几何距离；dti表示接收机钟差；dtk表示卫星钟差；d i表示接收机伪距硬件延迟；d k表示卫星端伪距硬件延迟；λ表示波长；φi表示接收机端初始相位；φk表示卫星端初始相位；δi表示接收机端相位硬件延迟；δk表示卫星端相位硬件延迟；表示整周模糊度表示观测噪声。

测站i、j间做差，得到单差模型：

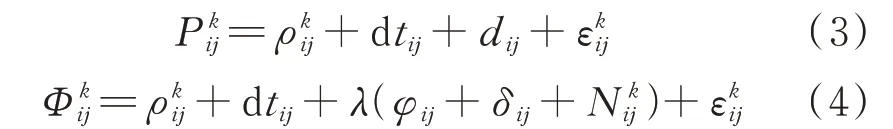
式中，和表示单差相位观测值与伪距观测值；表示单差站星间几何距离；dtij表示单差接收机钟差；d ij表示单差单差接收机端伪距硬件延迟；φij表示单差接收机初始相位；δij表示单差接收机端相位硬件延迟；表示单差整周模糊度；表示单差观测噪声；其他符号含义与式（1）、式（2）一样。

在利用紧组合模型进行相对定位时，GPS与QZSS选择1颗卫星作为参考星，在两个系统间作双差，选择1颗GPS卫星作为参考卫星，GPS/QZSS双差模型为：

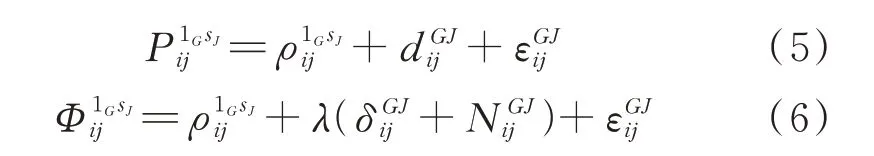
式中，G表示GPS；J表示QZSS；sJ表示QZSS卫星；和表示系统偏差；其他符号与之前表示相同。

对系统偏差与模糊度进行重组，可得：

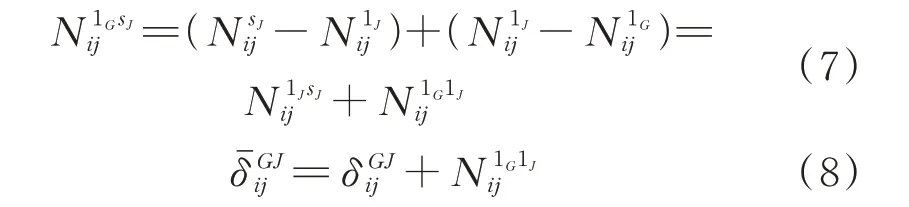
进一步得到紧组合模型

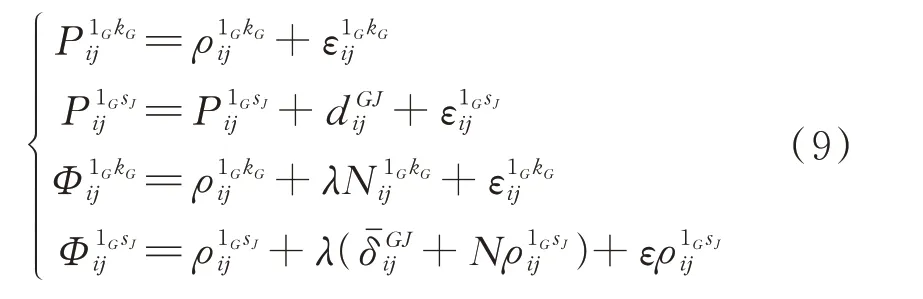
2 实验分析

为详细分析GPS/QZSS紧组合和松组合两种模型短基线相对定位性能，采用IGS机构发布的TID1站和STR1站组成约9 km长的短基线，这两个跟踪站的接收机类型均为SEPT POLARX5，采样间隔为30 s，观测时间为2020年2月3日0—24时，能同时接收到GPS和QZSS卫星信号。在进行数据处理分析时，主要评估不同高度角情况下两种模型的定位精度与模糊度固定情况，考虑到当前GPS播发L 5频率的卫星较少，因此只对GPS/QZSS兼容频率L 1、L2、L1/L2等3种情况下的数据进行解算，并同时计算出两种模型下的卫星可见数与PDOP（position dilution of precision）值情况。

2.1 系统偏差

利用紧组合模型进行相对定位时，为消去其他误差的影响，一般采用零基线或者短基线差分系统间偏差（differential inter-system bias，DISB），选用同样由IGS机构发布的YARR站和YAR3站组成的超短基线，长度为110 m左右，观测时间、采样间隔与接收机类型与之前所选测站相同。由于GPS发展比较成熟，选取GPS其中一颗卫星作为参考卫星，进行GPS与QZSS系统间偏差评估。

图1给出了GPS/QZSS组合L 1、L 2、L 1/L 2不同频率伪距与载波DISB情况，表1给出了DISB的统计情况。从图1和表1可以看出，3种频率伪距DISB在±1 m范围波动，载波DISB在±0.1周范围内波动，3组伪距DISB标准差（standard deviation，STD）均在0.02 m以内，载波DISB标准差均在0.001周以内，考虑到伪距与载波的精度，且伪距DISB和载波DISB绝对量接近0，认为在观测时段内，系统偏差较为稳定，且可以忽略不计。

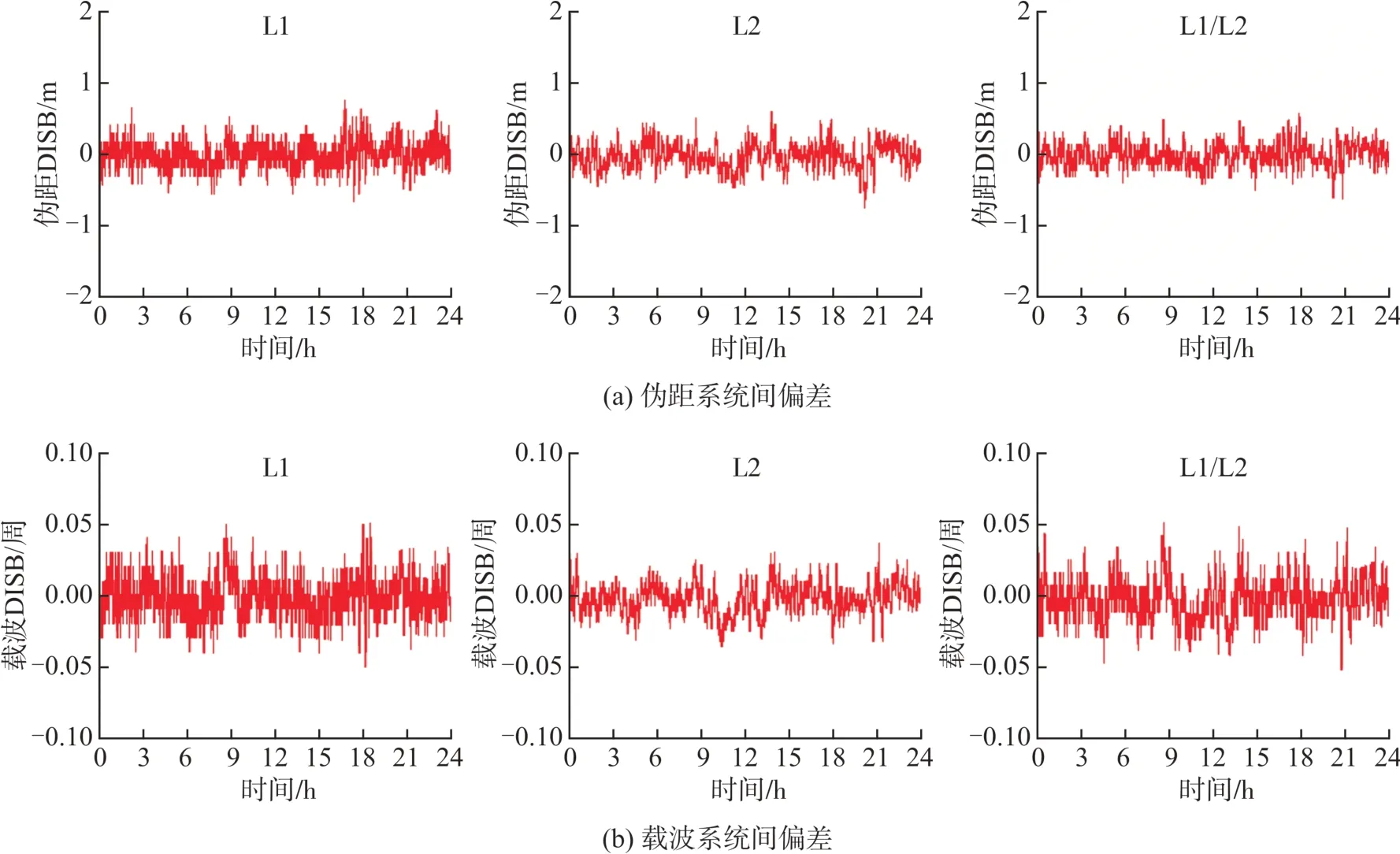
图1 GPS/QZSS重叠频率系统间偏差Fig.1 GPS/QZSS Overlapping Frequency DISB

表1 GPS/QZSS重叠频率间DISB统计Tab.1 DISB Statistics Between GPS/QZSS Overlapping Frequencies

2.2 数据处理分析

根据实验所选取TID1站和STR1站组成的短基线数据，采用两种数据处理方案进行数据处理：

1）截止高度角分别设置为10°、15°、20°、25°和30°时，对GPS/QZSS组合L 1、L 2单频以及L1/L 2双频组合3种情况下的数据，采用紧组合模型进行解算；

2）截止高度角分别设置为10°、15°、20°、25°和30°时，对GPS/QZSS组合L 1、L 2单频以及L 1/L 2双频组合3种情况下的数据，采用松组合模型进行解算。

根据解算得到的结果，计算统计两种模型不同情况下的定位精度与模糊度固定情况。限于篇幅原因，本文给出的都是截止高度角为30°时，松组合和紧组合模型的卫星可见数、PDOP值、Ratio值以及定位误差。

从图2可以看出，在观测时段内，紧组合模型的卫星可见数比松组合多一颗，而紧组合的PDOP值略小于松组合，为进一步细化，在截止高度角为30°时，紧组合模型的平均卫星可见数为6颗、平均PDOP值为2.86；松组合模型的平均卫星可见数为5颗、平均PDOP值为3.16。综上所述，由于选取参考卫星不同，紧组合模型下的卫星可见数与卫星空间几何分布情况优于松组合模型。

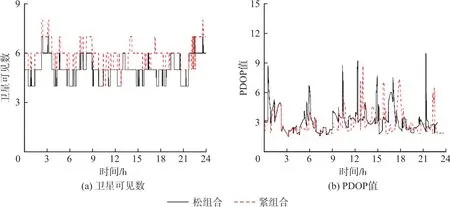
图2 截止高度角为30°时卫星可见数和PDOP值Fig.2 Satellite Visible Number and PDOP Value when the Elevation Mask Angle is 30°

2.2.1 模糊度评估

评估松组合和紧组合模型模糊度固定情况时，主要评估两种模型的模糊度固定历元数与固定错误历元数。模糊度解算时，将Ratio值设置为2，因此Ratio值大于2表示历元固定成功，固定错误历元是指模糊度在固定时出现错误的历元，模糊度真值则是通过多历元的模糊度值进行平滑计算得到。

由图3可知，在高度角较大，卫星可见数较少的不良观测条件下，3个频率紧组合模型的Ratio值明显优于松组合模型，表明紧组合模型相比松组合模型更能有效提升模糊度的固定性能。

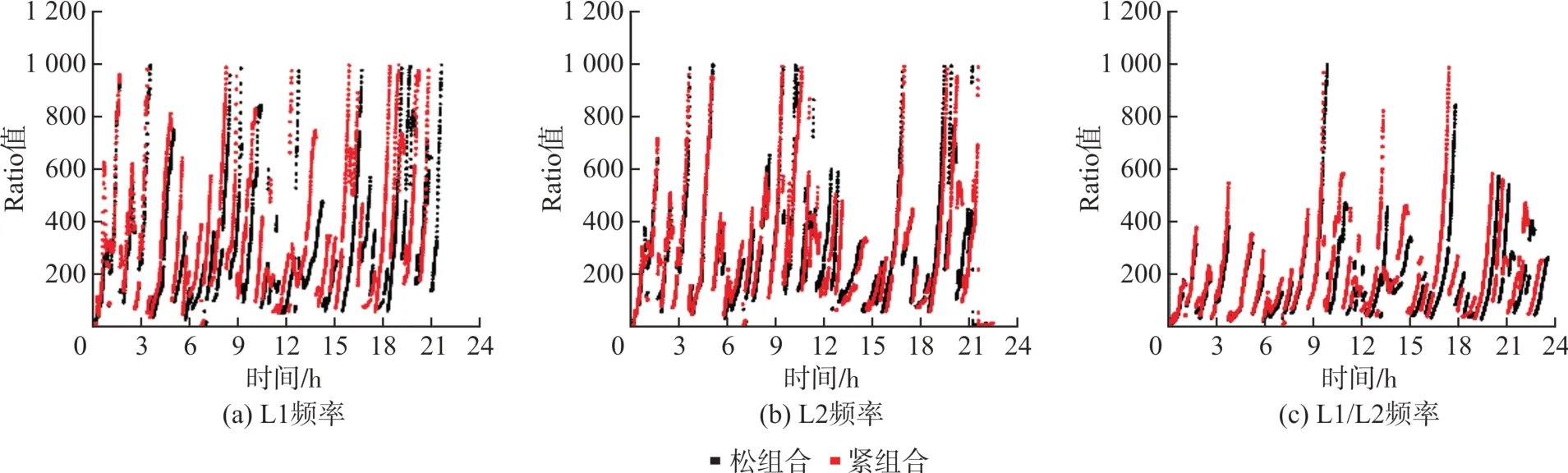
图3 截止高度角为30°时Ratio值Fig.3 Ratio Value when the Elevation Mask Angle is 30°

表2为详细统计的模糊度固定情况。由表2可知，截止高度角为10°～30°时，两种模型的模糊度固定正确率一样，为100%；截止高度角为10°～25°时，两种模型的模糊度固定情况相当；截止高度角达到30°时，紧组合模型的模糊度固定历元数要多于紧组合模型，其中L 1频率紧组合模型固定历元数比松组合多24个、L2频率多9个、L 1/L 2组合频率多7个。

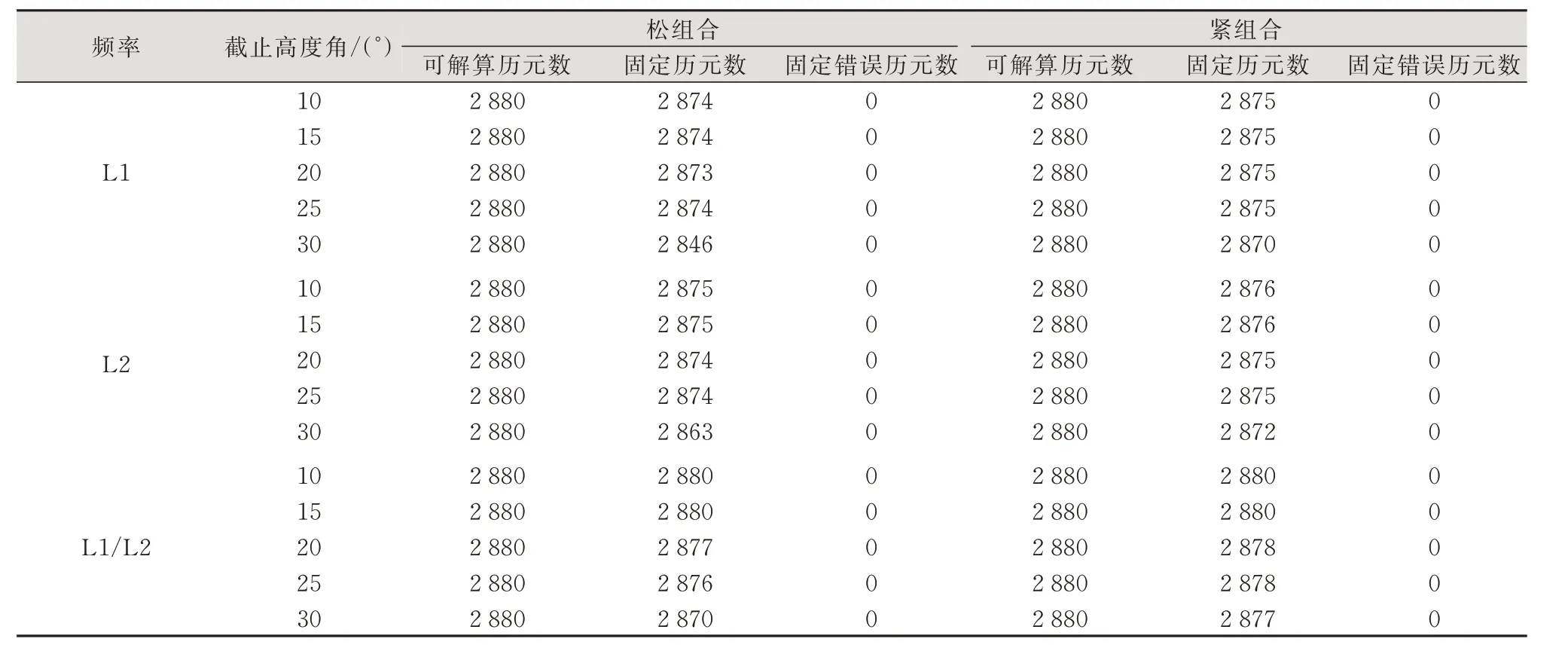
表2 松组合和紧组合单历元模糊度固定情况统计Tab.2 Statistics of Fixed Epoch Ambiguity of Loose Combination and Tight Combination

2.2.2 定位精度分析

在计算分析两种模型短基线相对定位精度RMS（root mean square）前，先联合周围跟踪站，利用GAMIT软件计算得到所选跟踪站坐标真值，然后计算得到流动站每个历元的坐标，通过各历元坐标值与坐标真值作差，得到两种模型短基线相对定位误差与精度。

从图4可以看出，在短基线相对定位中，紧组合和松组合两种模型解算得到E、N、U 3个方向的定位误差序列变形趋势一致，紧组合模型解算得到的定位误差略小于松组合模型。

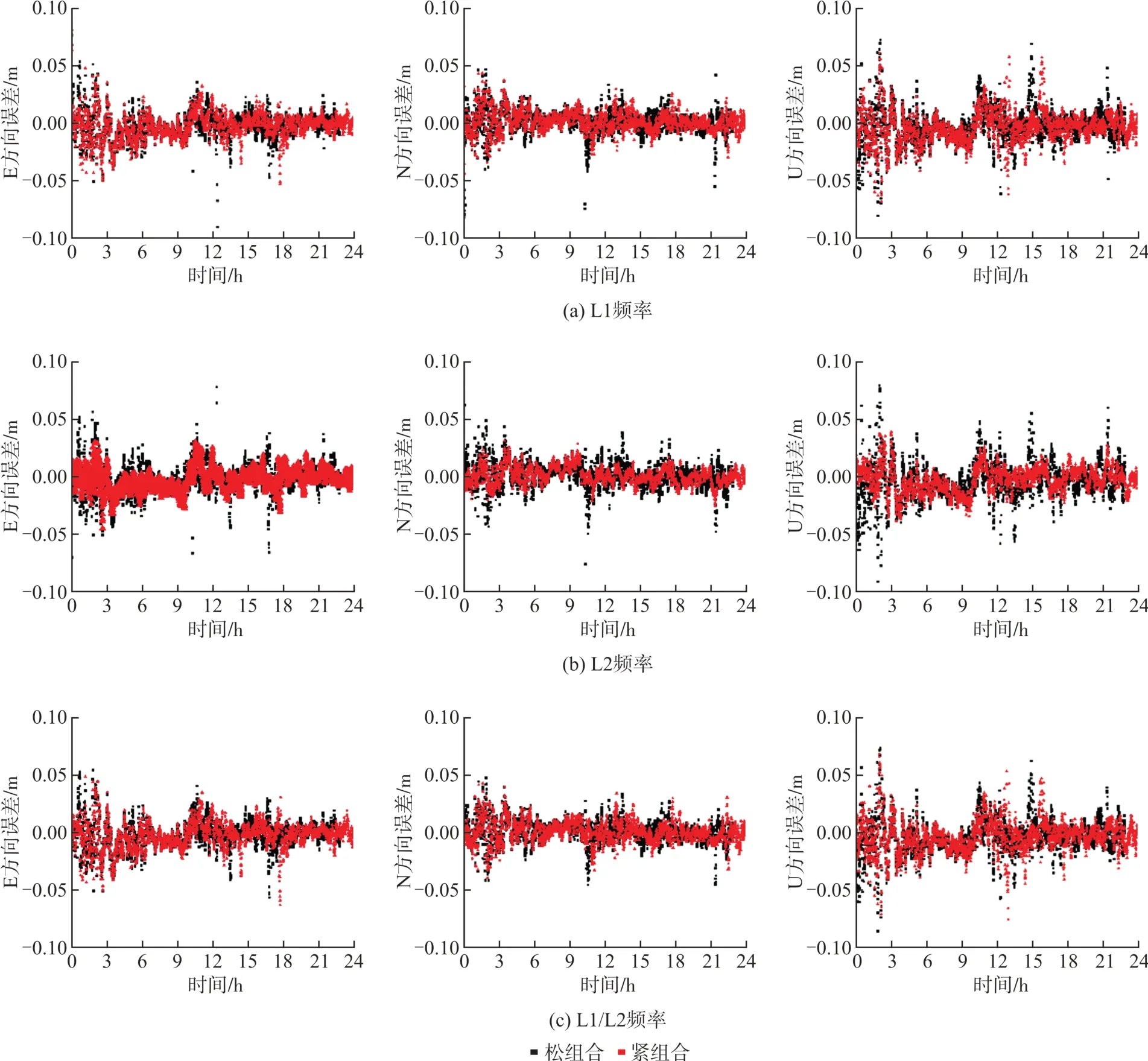
图4 截止高度角为30°时GPS/QZSS组合L 1/L 2频率正确固定解松组合和紧组合定位误差Fig.4 GPS/QZSS L 1、L 2、L1/L 2 Frequency Is Fixed Correctly when the Elevation Mask Angle is 30°

为了进一步详细分析松组合和紧组合两种模型下短基线的相对定位精度，对L 1、L 2、L 1/L 2不同频率、不同截止高度角、不同方向的定位精度进行统计，统计结果如表3所示。从表3可以看出，当高度角在10°～25°之间，紧组合和松组合模型下的定位精度相当，与模糊度固定情况表现一致。当截止高度角达到30°时，紧组合模型相比松组合模型定位精度有了较大提升，对于GPS/QZSS组合L 1频率，E、N、U 3个方向分别提升了14.73%、14.06%、16.80%；对于GPS/QZSS组合L 2频率，E、N、U 3个方向分别提升了9.90%、12.75%、16.67%；而对于GPS/QZSS组合L 1/L 2频率，E、N、U 3个方向分别提升了10.71%、10.13%、12.62%。

表3 松组合和紧组合模糊度正取固定时定位精度RMS统计Tab.3 Statistics of the Positioning Accuracy（RMS）when the Ambiguities of Loose and Tight Combinations are Fixed

3 结束语

基于IGS跟踪站组成的短基线GPS/QZSS重叠频率实测数据，本文推导了GPS/QZSS紧组合RTK定位原理，评估了GPS/QZSS间的系统偏差和模糊度固定情况，对比分析了松组合和紧组合两种模型下GPS/QZSS定位精度，经研究发现：

1）紧组合模型下的卫星可见数与卫星空间几何分布结构略优于松组合模型，这可能是因为紧组合模型只选取一颗参考卫星，而松组合模型要选取两颗；

2）相同类型接收机组成的短基线，重叠频率伪距与载波DISB几乎为0，在进行数据处理时可以忽略不计，与文中选取文献分析结果一致；

3）通过对比不同高度角情况下松组合和紧组合定位性能，发现在高度角较大、卫星可见数较少的环境下，紧组合模型相比于松组合模型更能有效提升模糊度固定率，同时发现紧组合模型使短基线相对定位精度也有明显提升，其中U方向定位精度提升最为明显。

相较于其他对于GPS/QZSS紧组合模型的分析，本文详细分析了不同截止高度角下GPS/QZSS紧组合模型短基线相对定位精度。但只分析了GPS/QZSS紧组合模型短基线相对定位精度，在后续研究中，将进一步融合其他其他导航系统兼容频率，相信RTK（real-time kinematic）定位精度将会进一步提升，为今后高精度RTK定位研究提供一定的参考意义。