垂线偏差对超长隧道横向贯通误差影响的分析与研究

何金学

1中铁第一勘察设计院集团有限公司测绘地理信息技术工程研究院，陕西 西安，710061

GNSS技术已广泛应用于隧道（尤其是超长隧道）洞外平面控制测量［1］，然而GNSS测量成果属法线系统，隧道平面控制测量中的进洞联系测量和洞内平面控制测量成果属垂线系统，二者存在系统差别，即垂线偏差（通常指过地面点的垂线方向与该点至正常椭球面法线方向间的夹角）［2］。垂线偏差是影响联系测量方向精度的主要系统误差，而联系测量的方向精度将直接影响洞内平面控制网的精度和隧道的横向贯通精度。

对于高精度隧道平面控制测量而言，控制其横向贯通精度是保证隧道顺利贯通的关键，而垂线偏差对隧道横向贯通误差的影响主要取决于两端洞口后视方向的误差、观测方向的高度角和方位角。受地形因素的限制，在崇山峻岭中修建隧道时，洞外控制点与进洞联系点间的高差较大，需要的高度角也较大，因此导致的垂线偏差对隧道横向贯通误差的影响不可忽略［3，4］。

目前测定垂线偏差的方法主要包括天文大地测量法、重力测量法、地球重力场模型法、GNSS水准法和数字天定摄影仪法等［5］。其中，重力测量方法和天文大地测量方法属于间接测量方法，计算时首先需要精确测定全球或局部区域范围内的重力异常数据，这两种方法均可获得精度更高的垂线偏差值，但这两种方法的解算过程比较复杂，在隧道控制测量过程中，十分精确地测定各控制点的垂线偏差值是不现实且没有必要的，且对于线路工程测量而言，通常里程跨度极大，区域范围内的重力异常数据往往不易获取。天文大地测量方法和GNSS水准测量方法属于直接测量方法，可通过对观测数据的相关计算直接获得垂线偏差［6］。目前隧道洞外平面控制网基本采用GNSS方法布设，采用天文大地测量方法需要通过天文测量获取天文坐标，而GNSS水准测量方法无需进行天文测量，仅需联测一定量的GNSS水准点即可，因此对于隧道平面控制测量而言，采用GNSS水准测量方法是获取垂线偏差最快捷的方法。

1 GNSS水准垂线偏差计算方法

采用GNSS水准测量方法测定垂线偏差时，首先需要测定高程异常值，通常将GNSS测量技术与精密水准测量技术相结合以获取区域的高程异常值［7］。在地势起伏较大的区域，当水准测量不便实现时，可采用精密三角高程测量结果代替二等水准测量结果［8］。

由大地测量学可知，大地水准面差距N与垂线偏差δ存在如下微分关系［9］：

式中，s为大地水准面沿任意方向上铅垂面与参考椭球面交线的长度。

垂线偏差通常被分解成子午分量ξ与卯酉分量η，它们与投影面的大地方位角A的关系为［10-12］：

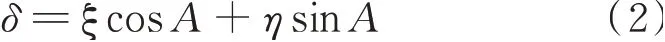
联合式（1）和式（2）得：

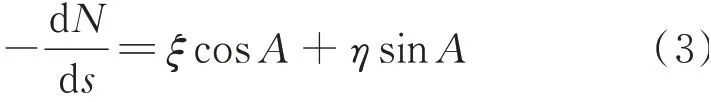
用差值代替上式中的微分值，可得：

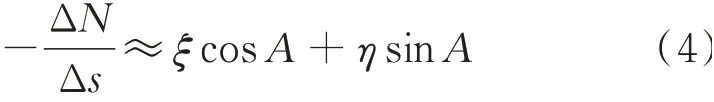
式中，ΔN为两点大地水准面差距之差，即高程异常差。

当采用GNSS方法测定A、B两点的基线时，基线两端点高程异常差与这两点的正常高H和大地高h的关系如下：

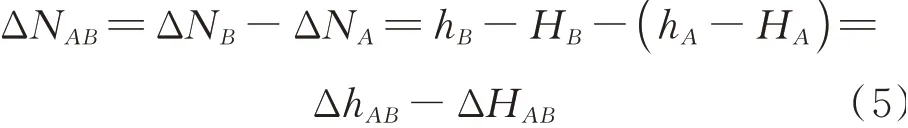
由式（4）和式（5）进一步可得：

若某点存在两条基线边，则δ计算公式如下：

式中，A1、A2分别为沿基线观测方向的大地方位角。

通过联立式（6）、式（7）即可获得该点垂线偏差的子午分量ξ和卯酉分量η：

由式（8）可知，ξ和η的大小主要受基线间夹角的影响，当A1-A2接近90°时，计算的垂线偏差分量ξ和η精度最优，因此，利用GNSS水准测量方法测定垂线偏差时，应注意基线边夹角的影响，在布设洞外GNSS控制点时，应使基线边夹角不宜过小，否则会影响垂线偏差分量的计算精度。

2 垂线偏差对隧道横向贯通误差的影响

根据大地测量学，垂线偏差改正值可由式（9）计算［13］：

式中，ξj和ηj分别为测点j的垂线偏差在子午和卯酉方向上的分量；A ji为方位角；αji为高度角。

设由i、j、k三点组成的角度为βj，则以法线为准的角度和以垂线为准的角度的差别为［14］：

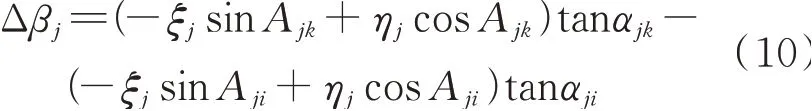
由式（9）和式（10）可知，当隧道洞外GNSS后视定向边两端点的高程基本相等（即α≈0）时，垂线偏差对观测方向的影响ΔL≈0，当αji和αjk均接近于零时，即i、j、k三点基本处于同一个高程面上时，Δβ≈0，对于长大隧道而言，主洞段导线多为直伸型，因此主洞段导线测量受垂线偏差的影响较小；当斜井为直伸且坡度比较均匀时，αji≈-αjk，则有Δβj≈0，隧道斜井支洞段的洞内导线测量受垂线偏差影响可较小。

由以上分析表明，垂线偏差通过影响定向边的坐标方位角来对隧道横向贯通的误差造成影响。

根据各GNSS控制点和进洞联系测量点的坐标和水准高程，即可计算不同后视定向边由垂线偏差引起的横向贯通误差影响值。按最不利条件进行估计，在顾及垂线偏差影响时，横向贯通误差估计值可表示为［15］：

式中，Δ横为隧道横向贯通误差综合影响值；Δ垂为垂线偏差对隧道横向贯通误差的综合影响值；m洞内、m洞外分别为洞内、外控制测量误差对横向贯通误差影响值的中误差；Δ进、Δ出分别为隧道进、出口处垂线偏差对横向贯通误差的影响值；ΔL为后视定向边坐标方位角的垂线偏差改正（即后视定向边误差）；S为定向边端点至贯通面的垂直距离。

由式（12）可知，垂线偏差对隧道横向贯通误差的影响主要反映在后视定向边的误差上，因此，当洞外GNSS控制点与进洞联系点间存在高差时，进洞联系测量过程中坐标方位角向洞内传递必然会受垂线偏差的影响，从而影响隧道的横向贯通精度，增大其横向贯通误差。

3 实例分析

针对输水隧洞5#、6#支洞洞外控制点间高差大、贯通距离长的特点，本文进行了垂线偏差对隧道横向贯通误差影响的计算实验。洞外控制点位置图及5#、6#支线控制网图如图1所示。

图1 控制点位置图Fig.1 Location Map of Control Points

根据5#、6#支洞洞外各GNSS控制点的GNSS测量数据和水准测量数据，选取基线边夹角较好的边计算了各控制点垂线偏差的子午分量ξ和卯酉分量η，计算结果见表1。同时根据洞外相关数据计算了5#、6#支洞选取不同后视定向边时垂线偏差对横向贯通误差的影响值，计算结果见表2。

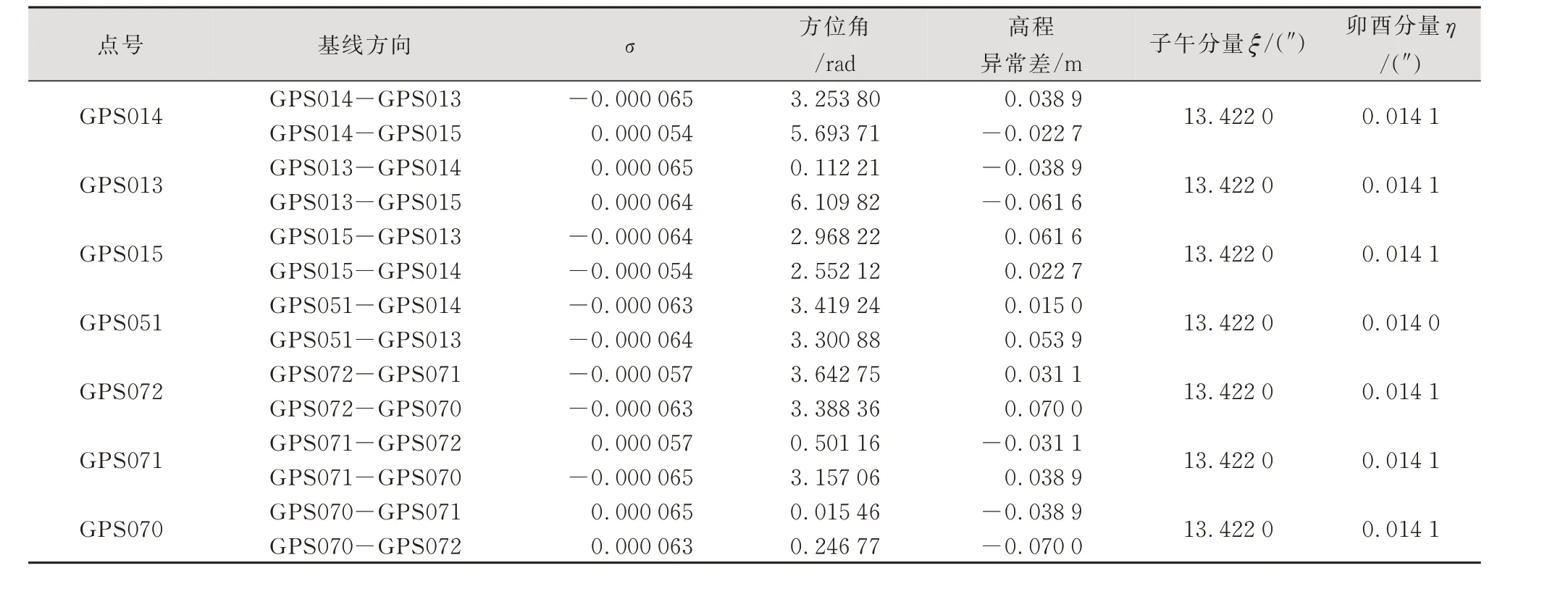
表1 洞外GNSS控制点垂线偏差子午分量ξ与卯酉分量η计算结果Tab.1 Calculation Results ofξandηComponent of Vertical Deviation of GNSS Control Points Outside the T unnel

由表2可知，选择不同的后视定向边和进洞方向时，垂线偏差对横向贯通误差的影响差异明显，以GPS013→GPS014为后视定向边，进洞方位选GPS014→X01-Y时，垂线偏差对横向贯通误差的影响值达到122.00 mm，而以GPS014→GPS013为后视定向边，进洞方位选GPS013→X01-Y时，垂线偏差对横向贯通误差的影响值仅为1.11 mm。

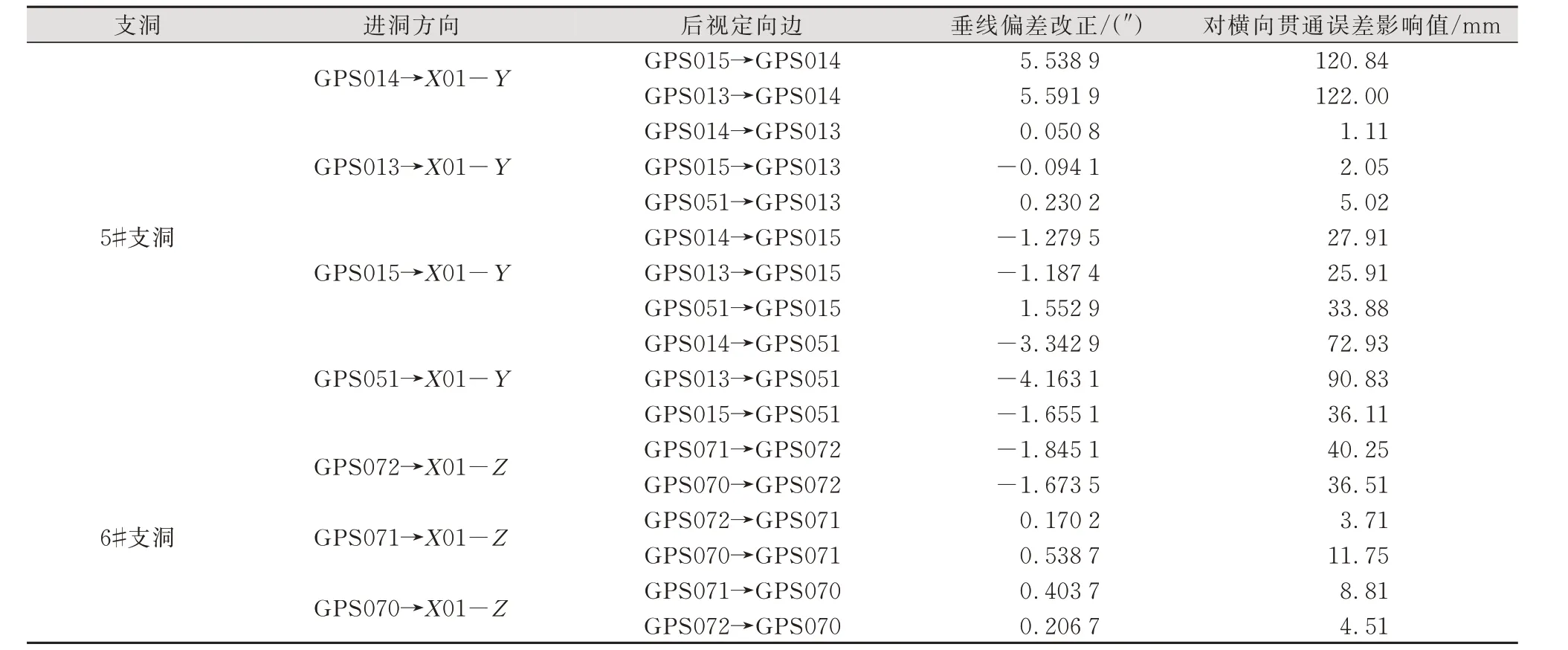
表2 垂线偏差对横向贯通误差影响值计算结果Tab.2 Calculation Results of Influence Value of Vertical Deviation on Transverse Penetration Error

根据支洞外控制点的布设情况，通过式（12）计算了不同后视定向边选择方案垂线偏差对横向贯通误差的综合影响值，并统计了最小值和最大值对应的后视定向边选择方案，统计结果如表3所示。

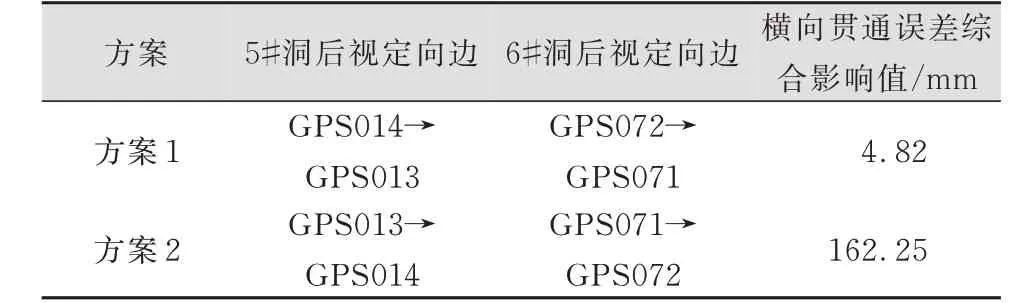
表3 不同后视定向边选择方案引起的横向贯通误差的综合影响值Tab.3 Comprehensive Influence Value of Transverse Penetration Error Caused by Different Rear-View Directional Edge Selection Schemes

由表3可知，选择精度最优的后视定向边，可显著减小垂线偏差对隧道横向贯通误差的影响，从而有效提高隧道的横向贯通精度。

4 结束语

本文通过GNSS水准法计算垂线偏差和垂线偏差对隧道横向贯通误差的影响理论分析，并以超长输水隧洞5#、6#支洞为实例进行了实验，结论如下：①复杂山区超长隧道横向贯通误差计算时垂线偏差的影响不可忽略；②垂线偏差的影响主要反映在后视方位边上，为提高隧道测量的贯通精度，应选取最优的后视方位边引测方位进洞；③后视方位边两端控制点的高程与洞口设计高程宜保持一致，以减小垂线偏差对隧道横向贯通误差的影响；④在布设洞外GNSS控制点时，应综合考虑垂线偏差的影响，基线边夹角不宜过小，否则会影响垂线偏差分量的计算精度。