“垂直”重难点解读

同学们在小学里就已经对“垂直”有了初步的认识，在《平面图形的认识（一）》这一章中，课本通过图片和“议一议”活动，在具体情境中进一步丰富了对垂直的认识，实现从感性认识到理性认识的转变.

一、与垂直有关的基本概念

1.垂线的定义：如果两条直线相交所成的四个角中有一个角是直角，那么这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.

2.垂线段的定义：垂线上一点到垂足之间的线段.

3.点到直线的距离：直线外一点到这条直线的垂线段的长度.

二、概念辨析

垂线是一条直线，可以向两端无限延伸，不可以度量；垂线段是垂线上的一条特殊的线段，可以度量；点到直线的距离是垂线段的长度.

垂线、垂线段都是图形，点到直线的距离是数量.

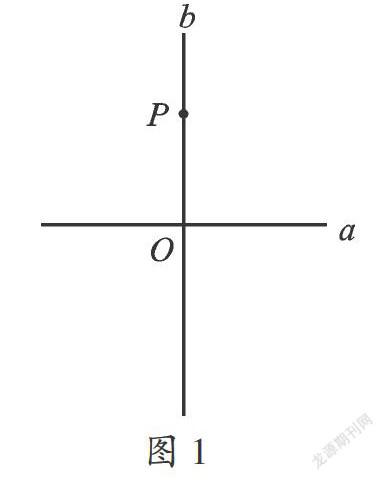
如图，直线 ⊥ ，直线 叫做直线 的垂线，直线 也叫做直线 的垂线；线段OP叫做点P到直线 的垂线段；垂线段OP的长度是点P到直线 的距离.

例1.下列说法中，错误的个数是（ ）

①若两条直线相交，所得的四个角中有一个角是90°，则这两条直线一定互相垂直；

②两条直线的交点叫做垂足；

③直线AB⊥CD，也可以说成直线CD⊥AB；

④同一平面内的两条直线不是平行就是互相垂直.

A.0个 B.1个 C.2个 D.3个

【分析】根据两条直线垂直的定义，只要两条直线相交所成的四个角中有一个角是直角，那么这两条直线互相垂直，所以①正确；只有两条直线互相垂直时得交点才能叫做垂足，所以②错误；两条直线互相垂直是相互的，所以③正确；两条直线在平面内的位置关系有相交和平行两种，垂直只是相交的特殊情况，所以④错误.

【解答】C

例2.下列说法正确的是（ ）

A.从直线外一点到已知直线的垂线段叫做这一点到已知直线的距离

B.过直线外一点画已知直线的垂线，垂线的长度就是这一点到直线的距离

C.画出已知直线外一点到已知直线的距离

D.连接直线外一点与直线上各点的所有线段中，垂线段最短

【分析】从直线外一点到已知直线的垂线段的长度叫做这一点到已知直线的距离，所以A错误；垂线是直线，可以无限延伸，无法度量它的长度，所以B错误；距离是数量，只能画出图形，所以C错误.

【解答】D

三、与垂直有关的性质

1.互相垂直的两条直线形成的四个角都是直角.

2.过一点有且只有一条直线与已知直线垂直.

注意：（1）“有且只有”包括两层含义：①过一点存在一条与已知直线垂直的直线；②过一点与已知直线垂直的直线是唯一的.（2）“过一点”可以是直线上一点，也可以是直线外一点.

3.直线外一点与直线上各点连接的所有线段中，垂线段最短.简单的说成是“垂线段最短”.

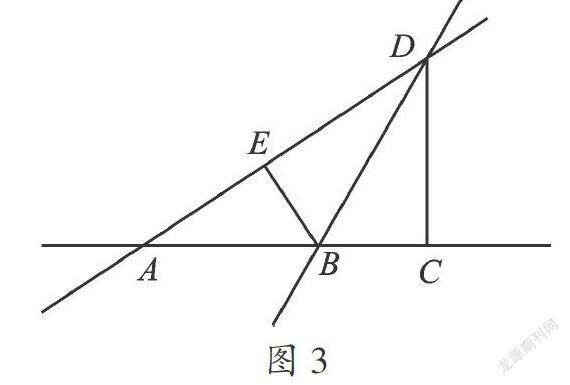
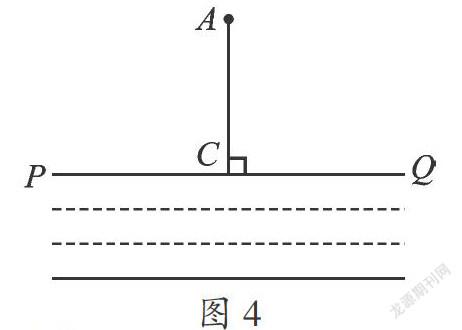
例3.如图，AD⊥BD，BC⊥CD，AB=5cm，BC=3cm，则BD长度的取值范围是（ ）

A.大于3cm B.小于5cm

C.大于3cm或小于5cm

D.大于3cm且小于5cm

【分析】根据垂线段最短，由AD⊥BD，BC⊥CD得BC

【解答】D

例4.如图，AC⊥CD，∠BED=90°.

（1）∠ACD=_______；

（2）直线AD与BE的位置关系是_______；

（3）在线段DA、DB、DC中，最短的线段是_______；在线段BA、BD、BE中，最短的线段是_______.

【分析】由垂直的定义能得到直角，反之两条直线相交所成的角中有一个角是直角，也能得到两条直线垂直.

【解答】（1）90°；（2）垂直；（3）DC BE

四、生活中的实际应用

例5.如图，修一条公路将村庄A与公路PQ连接起来，怎样修才能使所修的公路最短？画出路线图，并说明理由.

【分析】根据由一点到已知直线上所有点的连线中，垂线段最短，所以过点A作PQ的垂线段即可.

【解答】如图所示，线段AC就是所求的路线.

理由：垂线段最短.

例6.如图，在河岸 的同侧有一小镇A和自来水厂B，现要在河岸上建一抽水站D，将河中的水输送到自来水厂B处理后，再送往A镇.为了节省资金，铺设的水管应尽可能的短，抽水站D应建在何处，沿怎样的路线来铺设水管？试在图中画出路线图.

【分析】要使水管最短，则要使抽水站到自来水厂的距离和自来水厂到A镇的距离最短.

【解答】如图所示，过点B画直线 的垂线段，则垂足D为抽水站的位置.连接AB，沿D→B→A的路线铺设水管，可使得所用的水管最短.