耦合四连杆机构等效刚度计算
2022-09-05李培兴
黄 双, 武 欣, 李培兴
(上海工程技术大学 机械与汽车工程学院, 上海 201620)
纺织机械装备中,转子系统是重要的执行机构,如簇绒地毯织机和经编机等[1-3]。以簇绒地毯织机为例,簇绒地毯的织造质量主要取决于转子系统的运动平稳性和动力学特性,织造效率主要取决于转子系统的转速[4]。转子系统的振动会引起纱线的张力波动,使得纱线的喂纱量无法达到指定数值,从而影响地毯毯面质量[5-6]。转子系统的振动还会加速各配合零部件间的磨损,减少设备的使用寿命。另外,根据对簇绒地毯织机整机噪声源识别和定位可知,转子系统的结构振动是整机噪声的主要来源。因此,清晰了解转子系统的振动特性有着重要意义。为了准确求解转子系统的振动特性,各转子间耦合四连杆机构的等效刚度(包括线刚度和转动刚度)的取值尤为重要。
目前,关于多转子系统中耦合单元四连杆机构的等效刚度计算研究相对较少,大部分学者主要集中于研究四连杆机构的动力学和运动学特性。张建军等[7]利用欧拉公式建立了四连杆机构的动力学模型,采用MATLAB/Simulink建立运动学仿真模型,对四连杆机构中各构件的角位移、角速度和角加速度进行求解;郭文静等[8]利用MATLAB对铝锭连铸及接锭装置的运动轨迹、速度和加速度等运动特性进行分析;基于多体动力学原理,李园园等[9]运用四阶Runge-Kutta法分析铰链间隙关节位置、数量和润滑对空载四连杆机构的动力学响应特性。Tari等[10]提出了基于多项式法对柔性四杆机构的运动方程和静态方程解耦。
针对簇绒地毯织机转子系统,课题组采用能量法对针曲柄摇杆机构的等效线刚度和等效转动刚度进行研究,为转子系统中等效刚度的求解提供了一种新的思路。
1 簇绒地毯织机转子系统结构简介
簇绒地毯织机的转子系统如图1所示,由主轴、针轴和钩轴3转子组成,3转子之间由针曲柄摇杆机构和钩曲柄摇杆机构耦合而成。在针轴上,均匀布置着10套针摇杆滑块机构,通过滑块的往复上下运动,带动针排运动,完成针的穿刺运动。在钩轴上,均匀布置着10套钩摆杆机构,通过与针机构的精确配合,钩的左右摆动运动带动纱线形成绒圈。
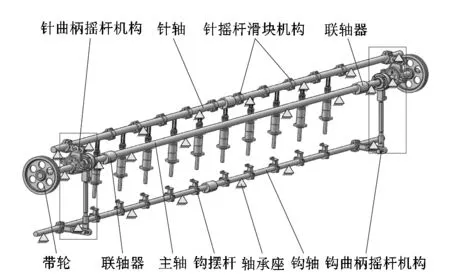
图1 簇绒地毯织机转子系统结构Figure 1 Structure of tufted carpet loom rotor system
在转子系统中,主轴和针轴之间通过针曲柄摇杆机构传递动力,主轴和钩轴之间通过钩曲柄摇杆机构传递动力。在求解转子系统振动特性(包括固有频率、临界转速和振型)等时,针曲柄摇杆机构需等效为具有线刚度Kh和转动刚度Kc的弹簧,如图2所示。为了得到正确的振动特性结果,等效线刚度和等效转动刚度的参数值显得尤为重要。
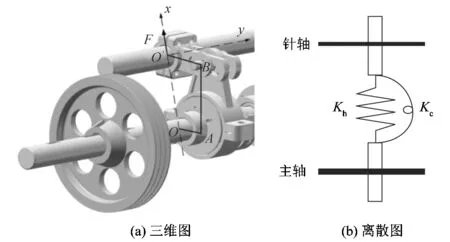
图2 针曲柄摇杆机构Figure 2 Schematic of needle crank rocker mechanism
2 基于能量法的等效刚度计算
2.1 能量法原理简介
根据能量守恒原理,积蓄在弹性体内的应变能Vε在数值上等于载荷所作的功W,即Vε=W。能量法是基于功能原理求解弹性体变形及位移等的一种方法。弹性体在拉伸、扭转和弯曲组合变形时,微段截面上内力有轴力F、扭矩Mx和弯矩M,分别产生的位移为d(Δl),d(θ)和d(φ)。已知弹性体的弹性模量为E,截面面积为A,剪切弹性模量为G,横截面的极惯性矩为Ip,横截面对中心轴的惯性矩为I。在弹性体微段上的应变能为各种内力在该微段上各自产生应变能的积,即:
(1)
若杆长为l,则
(2)
转子系统在正常运转下,针曲柄摇杆机构的结构一直处于运动状态。基于能量法求解等效刚度时,需将整个针曲柄摇杆机构看成36个刚架,每转动10°为1个刚架,通过求解每一个刚架的线刚度和转动刚度,从而得到曲柄摇杆机构在运动过程中的刚度值。
2.2 等效线刚度计算
以针曲柄摇杆机构为例,采用能量法进行求解。依据图2(a),针曲柄摇杆机构可以简化为如图3所示的刚架,将曲柄、连杆及摇杆视为OA,AB和BO′。图3中,li(i=1,2,3)为各杆长度,l4为OO′之间的距离。α,β和γ分别为杆l1,l2和l3与水平线之间的夹角。为了求得针曲柄摇杆机构的线刚度,对O′点施加单位载荷,即F=1 N,此时O′的位移值xO′的倒数为所求的线刚度Kh。在O′点施加单位载荷F后,分别对OA杆、AB杆和BO′杆进行受力分析,如图4所示。通过受力分析,各杆的轴力和弯矩值如表1所示。

图3 求解等效线刚度时施加的外力Figure 3 External force applied when solving equivalent linear stiffness

表1 各杆轴力和弯矩值
对于AB杆,为了满足受力平衡,需满足:
-Fl2sinγ+Fl3sinβ=Fl1sinα。
(3)
基于能量法可知,应变能Vε在数值上等于载荷所作的功WF,因此:
WF=Vε。
(4)
此时,
(5)
其中:
(6)
(7)
式中:E1,E2和E3分别为3杆件的弹性模量;A1,A2和A3分别为3杆件的平均截面面积;I1,I2和I3分别为3杆件横截面对中心轴的惯性矩。
通过式(5)、式(6)和式(7),可由式(8)求得xO′。
(8)
2.3 等效转动刚度计算
为了求解针曲柄摇杆机构的等效转动刚度,对O′施加单位弯矩M,即M=1 N·m,如图5所示。在施加单位力矩后,再次对OA杆、AB杆和BO′杆进行受力分析,如图6所示。通过受力分析,各杆的轴力和弯矩值如表2所示。

图5 求解等效转动刚度时施加的外力矩Figure 5 External torque applied when solving equivalent rotational stiffness

图6 各杆的受力分析图Figure 6 Stress analysis diagram of each rod
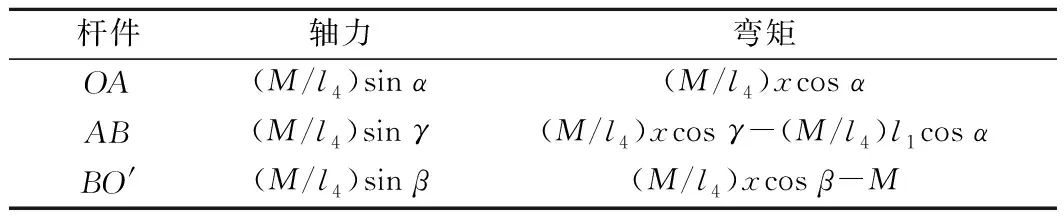
表2 各杆轴力和弯矩值
对于AB杆,为了满足受力平衡,需满足:
(9)
基于能量法,应变能Vε在数值上等于载荷所作的功WM,可知:
WM=Vε。
(10)
此时:
(11)
其中:
(12)
(13)
由式(11)~(13),可得:
(14)
3 参数计算及求解
3.1 参数计算
在簇绒地毯织机的针曲柄摇杆机构中,杆长l1=15 mm,l2=138 mm,l3=115 mm,l4=170 mm;弹性模量E1,E2和E3均为210 MPa;截面面积A1=0.033 0 m2,A2=0.008 1 m2,A3=0.013 2 m2;横截面对中心轴的惯性矩I1=1.49×10-5m4,I2=5.46×10-6m4,I3=2.35×10-5m4。针曲柄摇杆机构在转动过程中,各杆之间的角度关系如表3所示。

表3 角度参数值
3.2 求解及结果对比
将3.1中的各个参数代入式(8)和式(14),可求得针曲柄摇杆机构的等效线刚度和转动刚度。基于能量法所求得的Kh和Kc刚度值,如图7所示。图7(a)中,以曲柄的夹角0°为起始点,在曲柄为100°时,最大线刚度为3.46×106N/m;曲柄为280°时,最小线刚度为1.35×106N/m,平均线刚度为2.27×106N/m。图7(b)中,整体的针曲柄摇杆等效转动刚度在2.46×104~3.89×104N·m/rad之间变化,平均值为3.14×104N·m/rad。由于针曲柄摇杆机构的等效线刚度和转动刚度均变化较大,故在进行振动特性分析时,不能将该刚度值视为常数,应考虑时变参数对系统振动性能的影响。

图7 Kh和Kc刚度值与曲柄转角关系曲线Figure 7 Curve of stiffness value and crank angle of Kh and Kc
4 结论
课题组通过对各杆进行受力分析,采用能量法对多转子系统中的耦联四连杆机构等效线刚度和转动刚度进行了计算,并分析等效刚度的曲线特点。研究结果表明在求取振动特性时,等效线刚度和转动刚度为时变刚度。该结果为振动特性的求解提供了重要参数。对于不同的四连杆机构,其具体结构对刚度的计算结果有很大的影响,但本研究的方法和结果可作为一般借鉴。后续将采用实验方法对本结果进行进一步验证,并将讨论时变刚度对耦联轴系系统振动和噪声特性的影响。
