粘贴应变式车载称质量系统
2022-09-05李磅磅
温 辉, 李磅磅
(上海理工大学 机械工程学院, 上海 200093)
车载称质量系统是车辆安全治理和管理中重要的一环,该系统具有高效性、实时性和便捷性的优点。在车辆的行驶过程中,整车的受力及载荷的变化是不规律的,因此车载称质量系统的设计具有一定的复杂性。
从我国的公路、水路、铁路和航空运输来看,公路货运占有主导地位。为了追求经济效益,有些货车公司和车主安全意识不强,存在“病”车上路,违规驾驶和超载的情况。在全国范围内,每年仅汽车超载造成的交通事故和道路破坏,经济损失就高达数十亿元人民币,因此要引起重视并加强监管[1-3]。
车载称质量系统大致可分为2种:静态车载称质量和动态车载称质量。静态车载称质量是通过安装定点称量台(站),将车辆停靠在称量台(站)进行称量的一种方法。车辆动态称质量是在非停车状态下的一种称质量,具有省时、高效等一些特点[4-5]。正因为如此,全球在一些经济发达地区非常重视动态车载称质量技术,并推广应用。目前的动态车载称质量的方法大致可以分为[6-10]:①补偿法;② ADV法、DV法和V法;③位移积分法;④专家系统;⑤神经网络法;⑥参数估计法。
汽车悬架系统是每辆车必不可少的装置,传递作用在车轮和车架之间的力,缓冲由不平路面传给车架或车身的冲击力以减少振动。基于此,课题组采用有限元方法,考虑汽车悬架结构并结合惠斯顿电桥理论,设计了一种粘贴应变式车载称质量系统。而钢板弹簧是国内载货汽车的主要悬架系统,所以只要测得钢板弹簧的受力便可得出被测载荷。钢板弹簧的变形量很微小,并且安装于货车的不同部位,因此课题组提出了通过电阻应变片来测量板簧变形,并且采用多个含电阻应变片测量装置进行共同测量,从而实现数据的准确性。这样,车辆载荷与汽车悬架以及称质量传感器之间联系起来,构成了一个动态车载称质量系统。在设计完成粘贴应变式车载称质量系统整体结构之后还对称质量的标定方案进行分析,并提出一种多次车载称质量标定方案。
1 钢板弹簧的分析
粘贴应变式车载称质量系统是在对汽车悬架中钢板弹簧变形量的测量基础上建立的。因此,在对粘贴应变式车载称质量系统进行设计以及称质量标定之前,必须考虑钢板弹簧悬架系统的结构、钢板弹簧的接触受力以及钢板弹簧变形量与应力之间的关系。
1.1 钢板弹簧的结构分析
汽车上使用的多片钢板弹簧悬架系统通常由宽度相等、长度渐变的多片钢板弹簧组合而成。钢板弹簧叶片数量可以根据不同的汽车、不同运载量以及不同的用途而定,本研究以含7片叶片的钢板弹簧为例进行分析。多叶片钢板弹簧的总成如图1所示。
图1中多叶片钢板弹簧的模型是在非受力状态下的位置,当钢板弹簧受到纵向载荷时将发生挠曲变形。完整分析钢板弹簧的变形所需的边界条件是不同的力、压力、速度、支承和约束的条件集合。常态下钢板弹簧施加适量等效的纵向载荷,当弯曲变形达到水平位置则为最大挠度位置[11-12],即为承载的极限状态。下文均在板簧极限状态范围内进行有限元分析。

图1 多叶片钢板弹簧的总成Figure 1 Multi-leaf leaf spring assembly
1.2 钢板弹簧载荷-形变分析
利用ANSYS Workbench对2片及7片的钢板弹簧进行载荷-形变静力分析,以及对7片的钢板弹簧进行载荷-形变LS-DYNA动力分析。
如图2所示,通过对2片及7片的钢板弹簧进行了ANSYS静力学分析,以及对钢板弹簧进行LS-DYNA动力学验证,实验结果均说明:钢板弹簧的纵向形变和钢板弹簧受力始终呈线性关系[13]87。

图2 钢板弹簧载荷-形变分析Figure 2 Load-deformation analysis of leaf springs
1.3 整车中钢板弹簧载荷-形变分析
在实际情况中,货物在货车上的位置是随机的,并且有时装载的货物可能集中放在某个部位,这都将导致受力的不同。利用ANSYS Workbench 对在整车中钢板弹簧进行载荷-形变分析,分别对车辆货箱前端部位、中间部位和后端部位施加局部载荷以及对货箱整体施加均布载荷、随机载荷,对钢板弹簧纵向形变和受力进行仿真分析。
如图3所示,对整车在不同部位以及随机局部受载情况下的钢板弹簧载荷与形变的关系进行了分析。实验结果均说明:在整车中钢板弹簧的钢板弹簧纵向形变和钢板弹簧受力始终呈线性关系,与受力的位置无关。

图3 整车中钢板弹簧载荷-形变分析Figure 3 Load-deformation analysis of leaf springs in vehicle
2 粘贴应变片测量方案
由于钢板弹簧载荷与形变成线性关系,因此只需测量出钢板弹簧的形变量便可对汽车载荷与钢板弹簧形变之间的关系进行标定,从而得出货车的载荷。在测量形变的诸多方法之中,通过电阻应变片测量物体的形变以及应力是在实验中运用最多和最广泛的一种方法。通过电阻应变片测量形变的原理如下:首先选定合适的应变片;然后将选定的电阻应变片通过一定的方法进行安装,根据设计好的电路(常用惠斯顿电桥电路)使其粘贴在被测物体的表面;由于电阻应变片粘贴在被测物体表面,被测物体发生形变时,电阻应变片也随之发生形变,从而导致电阻应变片的阻值发生改变;因为电阻阻值的改变,电路中的电流电压也随之发生变化,测量出电流电压的变化从而转换求出被测物体形变[14-16]。通过这种方法可以将被测物体的形变量转化为桥式电路中的电流改变量,并且当变形量很小时,电路中电量变化也很小,这时可以采用放大电路对电量进行放大,从而对输出的数据进行处理得出所需要的测量值。
2.1 应变片测量电路设计
设计采用直流恒压电桥电路(即惠斯顿恒压电桥)。但在实际测量中,为克服零点漂移的问题,可在电路中串接零点漂移补偿电阻Rs来进行补偿;同理,对于电路中应变电阻阻值不同的问题则可以采用在电路中串联一个温度系数极低的平衡电阻Rt来进行补偿。直流恒压电桥电路中各桥臂的电阻阻值分别为R1,R2,R3和R4,各桥臂分别接入的是电阻应变片[13]84。补偿电路如图4所示。

图4 带补偿的惠斯顿电桥电路Figure 4 Wheatstone bridge circuit with compensation
2.2 粘贴应变片选型与粘贴
课题组设计的车载称质量系统粘贴于汽车悬架上,因此其工作温度为常温,所以选用的电阻应变片为常温应变片,其工作温度范围为:-30~+80 ℃。因为是动态车载称质量系统,对钢板弹簧应变的动态测量需要有快速的响应频率;又因为钢板弹簧受载波动频率高,因此所选的电阻应变片应具有较高的疲劳寿命。综上,疲劳寿命高和频率响应快的金属箔式应变片符合设计要求。如图5所示为车载称质量系统中使用的箔式全桥电阻应变片。

图5 箔式全桥电阻应变片Figure 5 Foil full bridge resistance strain gauge
所选应变片型号参数:类型为箔式全桥电阻应变片;电阻值为(350.0±17.5)Ω;灵敏系数为2.110±0.021;温度范围为-30~+80 ℃;应变极限为2%。
2.2.1 电阻应变片粘贴位置的确定
为了对钢板弹簧形变进行精确的测量,电阻应变片的贴片位置应选择钢板弹簧形变较大的区域。因此,选择将电阻应变片粘贴在带有卷耳的全长钢板弹簧叶片上[17]。
在确定了电阻应变片粘贴位置后,我们通过对如图6所示的钢板弹簧纵向形变与贴片位置的变化曲线分析可知,钢板弹簧中部位置的形变量最大,电阻应变片应该贴在中部。实际上在钢板弹簧中心处有盖板而无法贴片,因此贴片时在避开盖板后应尽量靠近钢板弹簧中部。

图6 钢板弹簧纵向形变随贴片位置变化曲线Figure 6 Variation curve of longitudinal deformation with patch positionof leaf spring
2.2.2 电阻应变片交叉贴片
在一些大型货车之中,汽车悬架系统非常庞大,且拥有多个钢板弹簧结构,可以采用交叉贴片的方法减少电阻应变片贴片的数量。
根据如图7所示的交叉贴片方案,当只贴1,3,6和8这4个位置时,车辆总载质量等于这4个位置读数的2倍。通过该方法可以减少应变片贴片的数量,达到提高经济效益的目的。

图7 交叉贴片示意图Figure 7 Cross-paste schematic
2.2.3 电阻应变片贴片工艺
课题组选用粘贴法对应变片进行贴片。应变片贴片工艺详细操作如下[18-19]:
1) 应变片的预处理。将选定好的应变片进行初步检查,主要是对阻值进行检测;再对应变片表面进行清洁处理,即采用无水乙醇对应变片表面进行擦拭,擦拭完后烘干备用。
2) 钢板弹簧贴片处的表面处理。为了使应变片粘贴更加牢固,须对试件贴片处表面进行预处理,且处理面积要大于应变片面积的3~5倍。首先,用砂纸打磨试件表面,打磨方向与贴片的方向成45°角;然后再用蘸有无水乙醇的脱脂棉球对其擦拭,并且擦拭时最好沿单一方向进行擦拭,多次擦拭直至脱脂棉球表面再无污渍;最后烘干即可。
3) 底层处理。在应变片粘贴之前,在钢板弹簧试件表面涂抹一层约为1.5倍应变片面积大小的底胶;底胶一般采用相同的粘贴剂,涂抹时胶水薄且均匀;最后再进行热固化处理。
4) 应变片的粘贴。首先在处理好的试件表面和应变片的底层涂上粘贴剂,晾干至粘贴剂开始略微发黏;然后将应变片准确地贴于试件表面,用手指轻轻按压,将里面的气泡以及多余的粘贴剂排出,使应变片和被测件完全粘合。
5) 固化处理。采用502快干胶对粘贴好的应变片进行固化,虽然使用502快干胶固化后粘贴疲劳寿命会有所下降,但是可以有效地减少零点漂移的现象,使测量结果更加稳定。
6) 粘贴质量的检查。在完成固化之后,应对应变片粘贴质量进行检查。为了测量结果的准确性,应变片粘贴后阻值变化不能超过0.5 Ω。
7) 连接导线-组桥。在完成应变片的粘贴之后可以通过锡焊的方式将应变片的引线与导线焊接在一起,组成测量需要的桥式电路;然后再用胶布将导线等固定。
在安装好应变片之后,为了使工作更加可靠,在保证高精度情况下长时间运行,可以在应变片上涂一层保护层来进行防护,如石蜡、松香和黄油的混合剂。
3 车载称质量标定方案
3.1 标定的理论分析
在完成贴片后,要实现从应变片形变导致电阻值变化引发电信号的输出到钢板弹簧载荷的过程,必须建立一个准确合理的标定方案对系统测量输出值进行标定,从而达到精确测量的效果。
应变片标定的目的是建立应变读数ε(电信号)与板簧载荷F的线性关系,建立线性关系至少需要2个坐标点,有2种做法。
1) 称质量1次。空载时读取应变读数ε0,给定载荷F1获得应变读数ε1,然后采集器内部通过编程可获得式(1):
(1)
2) 称质量2次。给定2个载荷F1和F2、获得2个应变读数ε1和ε2,然后采集器内部通过编程可获得式(2):
(2)
由式(1)、(2)可知,不论哪种做法,标定时必须知道各板簧的载荷。标定过程中若不考虑各板簧载荷,而仅考虑总载荷,那么一旦货物重心位置与标定时重心位置不同,则测得结果必然有误。
3.1.1 2轴货车标定理论分析
图8所示为2轴货车力学模型。其中2轴是指汽车的承重轴,可以根据轴距以及载荷的位置直接计算得到前后钢板弹簧载荷如下:

图8 2轴货车力学模型Figure 8 Two-axle truck mechanical model
(3)
3.1.2 3轴货车标定理论分析
图9所示为3轴货车受力示意。货物重力为G,重心到A轴的距离为l,重力载荷在车厢宽度方向上分布均匀,A,B和C轴板簧刚度分别为kA,kB和kC,计算A,B和C轴上的载荷。
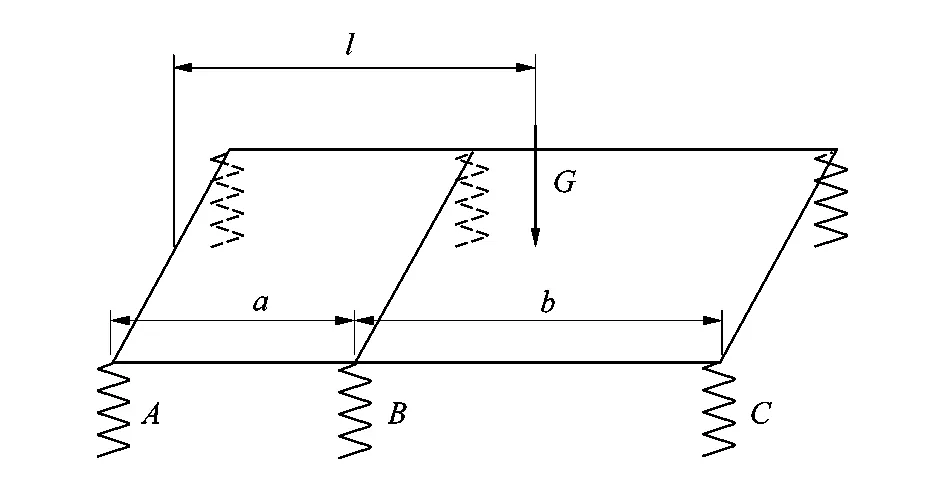
图9 3轴货车受力示意Figure 9 Schematic diagram of force of three-axle truck
由于不考虑货物在车宽方向上的不均匀分布,因而可将原问题简化为如图10所示的力学模型。
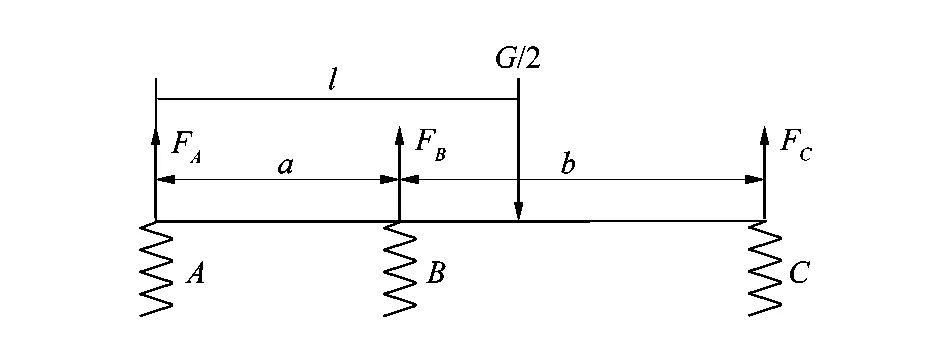
图10 3轴货车受力分析Figure 10 Force analysis of three-axle truck
根据受力分析,可得:
(4)
(5)
由式(4)和(5)可知,该问题有3个未知数,但是只能列2个平衡方程,因此需要补充几何方程。如图11所示,在受力变形后,车厢地板保持为直线(视车厢底板为刚体),因此可得:
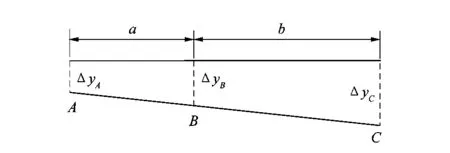
图11 几何协调条件Figure 11 Geometric coordination condition
(6)
已知kA,kB和kC,则可得:
(7)
将式(4)~(7)联立求解,可得:
(8)
若假设kA=kB=kC,则可得:
(9)
由式(8)~(9)可知:货物放置的位置对各钢板弹簧的载荷有着显著的影响,但无论货物如何放置,各钢板弹簧载荷之和总是等于货物质量。若要计算各板簧荷载,必须知道各种不同车型的轴距(可联系货车厂家或测量获得,然后根据车型建立数据库)以及板簧刚度(可联系货车厂家获得,或者根据车型做实验获得并建立数据库)。
3.1.3 标定方案
1) 对于双轴货车,由式(3)可知不存在标定困难。定制容量为500~1 000 L(具体所需容量需要通过实验确定)的可折叠的便携式塑料桶,筒身印有注水刻度线,桶底印有“十字”,方便用户测量筒体重心至前轴或后轴间距。水桶放置于车辆宽度方向的对称轴线上,注水后作为标定基准物。
2) 对于图9所示3轴货车,其后部2轴距离(B轴,C轴)板簧若相同,则kB=kC。另外,由于B轴和C轴距离较近,可近似认为B轴载荷和C轴载荷相同,即FB=FC,则可得:
(10)
当FB=FC时,车厢承载力学模型如图12所示。

图12 FB=FC时3轴货车力学模型Figure 12 Three-axle truck mechanics model at FB=FC
3) 其他特殊类型货车,可参照2)所述方法,在一定假设的基础上,得到板簧载荷近似计算公式。
4) 对于其他类型的多轴货车,若无法获得板簧刚度信息且无法简化计算,则可通过逐个标定的方法进行标定。例如,对于A轴板簧,将水桶放置于A轴上方,此时A轴板簧承担主要荷载,可近似认为A轴板簧载荷等于水桶重力的一半,据此进行标定。A轴板簧标定后进一步标定其他各轴板簧。
3.2 多次称质量标定方案
通过对车载称质量标定的理论分析,为了能够精确地测量出汽车的载质量,这里提出一种多次称质量标定的方案。
如图13所示,板簧载荷F和采集器读数D关系如下:
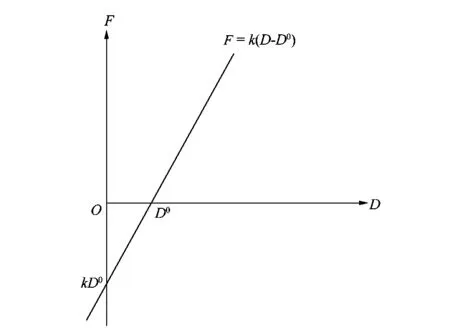
图13 板簧载荷与采集器读数关系Figure 13 Relationship between leaf spring load and collector reading
F=k(D-D0)。
(11)
式中:D0表示空载时的采集器读数,k为标定系数。
对于如图14所示的3轴货车力学模型,由竖直方向力的平衡方程可知:

图14 3轴货车力学模型Figure 14 Three-axle truck mechanical model
(12)
称质量3次,货物重心位置任意,重力分别记为G1,G2和G3;3板簧A,B和C标定系数分别记为kA,kB和kC。可得线性方程组,其中未知量为kA,kB和kC。可解条件是G1,G2和G3重心位置两两不重合。
(13)
对于轴数为N的货车,其N元线性方程组的表达式为:
(14)
在实际测量之中,为了减少应变片贴片数量简化操作,可采用如图7所示的交叉贴片的方法,此时多次称质量标定方案仍然可行。此时安装有4个应变采集器,其对应读数分别为D1,D2,D3和D4,对应的标定系数为k1,k2,k3和k4。对货车称质量4次,则可列方程组式(15),同理,解线性方程组可得k1,k2,k3和k4,由此可确定采集器读数与钢板弹簧载荷之间关系:
(15)
3.3 多次标定结果分析
通过对一辆常规半挂车实验可求解标定系数k1,k2,k3和k4,根据采集器读数D1,D2,D3和D4便可求得货车的载质量。我们采用多次标定方案对其进行标定,标定次数与相对误差如图15所示。由图可知,标定最大误差仅2%左右,具有良好的标定效果。

图15 标定次数-误差曲线图Figure 15 Graph of number of calibrations and error
4 结语
针对常规车载称质量系统效率低、系统庞大的问题,课题组设计了一种粘贴应变式车载称质量系统,且提出了一套完整的多次车载称质量标定的方案。对实验结果多次标定分析表明:该车载称质量系统精度高且标定结果稳定,能有效改善目前车载称质量状况,在车载称质量方面有广泛应用前景。
