椭圆旋轮线型罗茨泵转子型线设计

贲晨阳， 何雪明， 刘振超

(1.江南大学 机械工程学院， 江苏 无锡 214122；2.江南大学 江苏省食品先进制造装备技术重点实验室， 江苏 无锡 214122)

转子形状主要由转子型线决定，罗茨泵转子型线的设计，直接关系到罗茨泵性能的高低。

国内外专家学者对罗茨泵转子型线设计进行了具有价值的分析研究。王建等[1]建立基于流量脉动系数的齿轮泵中齿廓的主动设计的数学模型。邹旻等[2]分析了2转子间差动角对双啮合弦线转子泵流量脉动率的影响，提出了一种具有2对转子的双啮合弦线转子泵。杨舒然[3]基于齿廓啮合原理,建立了圆弧与其包络线、偏心渐开线与其包络线的啮合模型,提出了3种新型罗茨泵转子。黄龙龙等[4]对摆线泵进行CFD和FSI仿真，并将仿真结果进行对比。李玉龙等[5-6]基于渐开线齿廓的构造方法,提出了具有渐开线齿廓的转子型线，并为实现罗茨转子便捷高效的轮廓构造，提出了一种双对称图解法。Kang等[7]开发了一种新的转子型线，该转子型线由圆弧和摆线组成；通过体积计算和流场分析，分析不同型线对转子性能的影响。Hsieh等[8]利用共轭齿轮原理对罗茨泵摆线转子型线进行数学建模。Wu等[9]等建立多级罗茨真空泵IVEC型转子型线，提出了面积利用率和啮合间隙面积2个几何性能指标，用于评估转子型线的优劣。

传统的转子型线包括圆弧型、摆线型以及它们之间的发展和组合线型。然而以容积效率作为性能参数来评判罗茨泵转子型线的性能，传统转子型线性能普遍偏低。故课题组提出了一种椭圆旋轮线型转子型线，并详细推导了转子型线由叶峰曲线到叶谷线的设计算法，并分析了椭圆率对转子型线的影响。该型线的容积效率明显高于传统罗茨泵转子型线。

1 椭圆旋轮线转子型线设计

罗茨泵的2个转子形状是完全一样的，转子每个叶峰和叶谷[10]也是完全一样，且每个叶上的转子形状又是对称的。所以设计转子型线时，只需要设计1个叶或者半个叶上的齿廓，进而可以通过旋转和对称变换，将转子型线完整设计出来。

罗茨泵转子型线的节圆将单叶上型线分成了2个部分，分别为叶峰曲线和叶谷曲线。叶谷曲线在节圆内，叶峰曲线在节圆外。根据罗茨泵转子的工作原理，罗茨泵的左侧转子的叶峰曲线和右侧转子的叶谷曲线为共轭关系，所以只需设计左侧转子的一条叶峰曲线，通过包络法求解右侧转子的叶谷曲线，进而通过坐标转换得到左侧转子的叶谷曲线，完成整个转子的型线设计。

一条光滑曲线在另一条光滑曲线上做无滑动的滚动运动，光滑曲线上的一点的运动轨迹定义为广义旋轮线。当光滑曲线为圆时，圆做纯滚动形成的轨迹即为旋轮线，又称摆线[11]。当滚动圆换成滚动椭圆时，滚动椭圆上的一点轨迹也为一种旋轮线，可以将它定义为椭圆旋轮线。

建立罗茨泵转子坐标系如图1所示，其中包含了2对坐标系，分别是固结在罗茨泵泵体的左侧转子的静坐标系O1X1Y1和固结在右侧转子的静坐标系O2X2Y2；固结在罗茨泵泵体的左侧转子的动坐标系O1x1y1和固结在右侧转子的动坐标系O2x2y2；静坐标系不随着转子的转动而发生任何位置变化，动坐标系随着转子的转动发生相应角度的转动；R为罗茨泵转子的节圆半径；φ为罗茨泵转子的转角；ω为转子旋转的角速度。

图1 罗茨泵转子坐标关系Figure 1 Rotor coordinate relation of Roots pump

如图2所示，当滚动椭圆在纯滚动运动中围绕节圆的圆周逆时针旋转时，滚动椭圆上的点p的运动轨迹，即为椭圆旋轮线。定义椭圆的参数方程为：

图2 椭圆旋轮线轨迹Figure 2 Trajectory of elliptical rotary wheel line

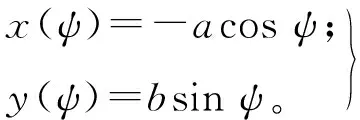
(1)

式中:ψ为椭圆参数角，a为椭圆长轴，b为椭圆短轴。

如图3所示，点A为椭圆开始滚动前圆与椭圆的接触点;当椭圆滚动一个角度θ时，点B′为椭圆和圆的接触点，可以看出椭圆上的曲线AB的长度等于椭圆在节圆上滚动经过的曲线AB′的长度。对椭圆弧长计算需要进行椭圆积分，则2条曲线的长度之间的关系可表示为:

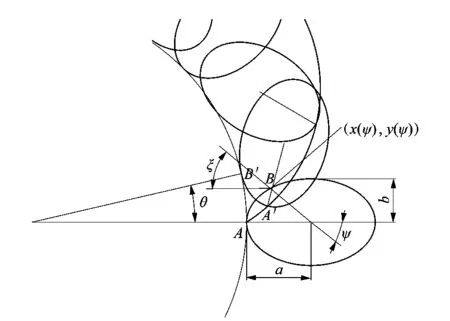
图3 椭圆旋轮线的几何关系Figure 3 Geometric relationship of elliptical rotary wheel line

(2)

式中：L为椭圆滚动1周的长度，rp为节圆的半径，θ为滚动椭圆在圆上滚动角。

(3)

得到了椭圆旋轮线型转子型线的叶峰曲线，可求解叶谷曲线：

(4)

则叶谷曲线的表达式为：

(5)

由三角函数中的辅助角公式[12]求解φ与参数θ的关系,需要分别求x1和y1对参数θ的导数。

(6)

其中：

求解出φ与θ的关系后，将φ代入式(5)中右侧转子的叶谷曲线，将叶谷曲线和叶峰曲线进行连接得到了1叶转子的四分之一型线，如图4所示。曲线CD为椭圆旋轮线型转子型线。

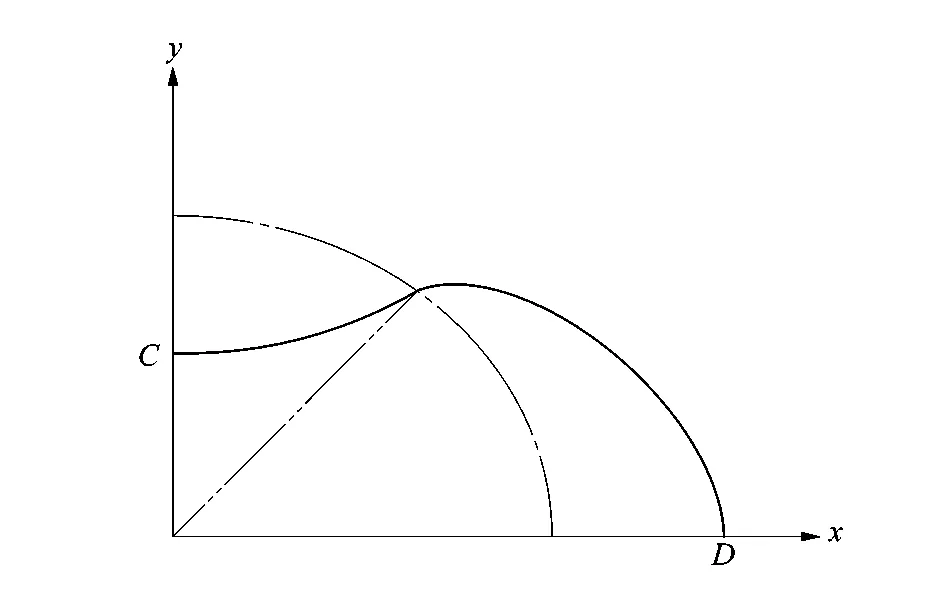
图4 椭圆旋轮线型转子型线Figure 4 Rotor profile of elliptical rotary wheel line type

2 椭圆率对转子型线的影响

2.1 椭圆旋轮线型转子型线根切条件

椭圆旋轮线是由椭圆在节圆上滚动形成的轨迹，其形状主要受椭圆短轴和椭圆长轴的比值影响，即椭圆率λ=b/a。不同的椭圆率会形成不同的椭圆旋轮线，当λ=1时，椭圆旋轮线即为摆线，构成的转子型线为常用的摆线型转子型线；当λ≠1时，转子型线为椭圆旋轮线型转子型线。

椭圆旋轮线型转子型线会产生如同齿轮设计过程中根切现象。出现根切的转子会使得转子的抗弯曲能力下降，重合度减少，影响转子运转的平稳性。

根据齿轮啮合原理[13]，得到罗茨泵转子的啮合条件：

vr2=vr1+v12=0。

(7)

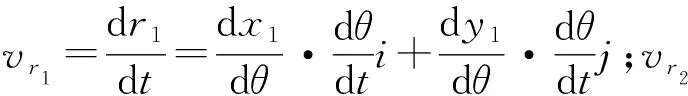
令：

(8)

则椭圆旋轮线型转子型线的根切条件为：

(9)

其中：

可将式(9)化简为：

(10)

2.2 椭圆率对转子型线的影响

针对不同椭圆率的转子型线情况， 设定转子的节圆半径rp为60 mm、转子叶数Z为2。将式(2)代入式(5),计算得到不同椭圆率λ对应的a,b和rp，其参数如表1所示。

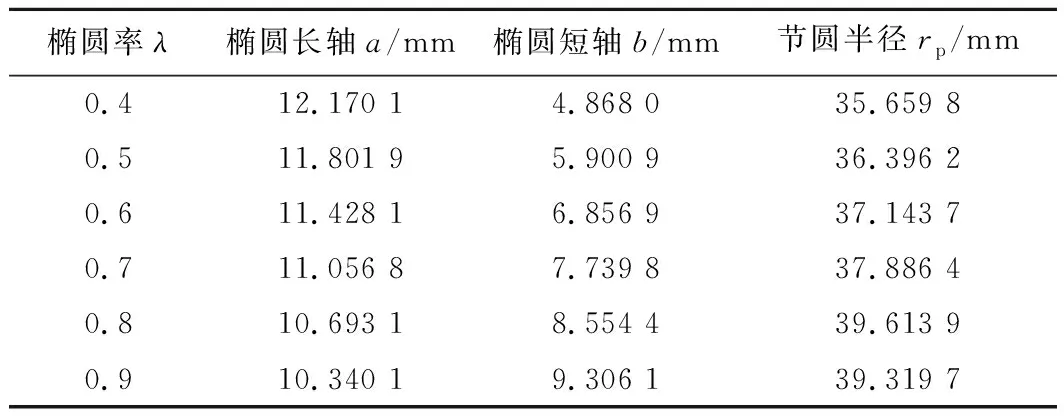
表1 不同椭圆率下转子型线参数

根据以上参数，绘制完整的转子型线，其中不同椭圆率下转子型线如图5所示。从图中可以看出，椭圆率越小，整个转子型线的凹凸性越明显。

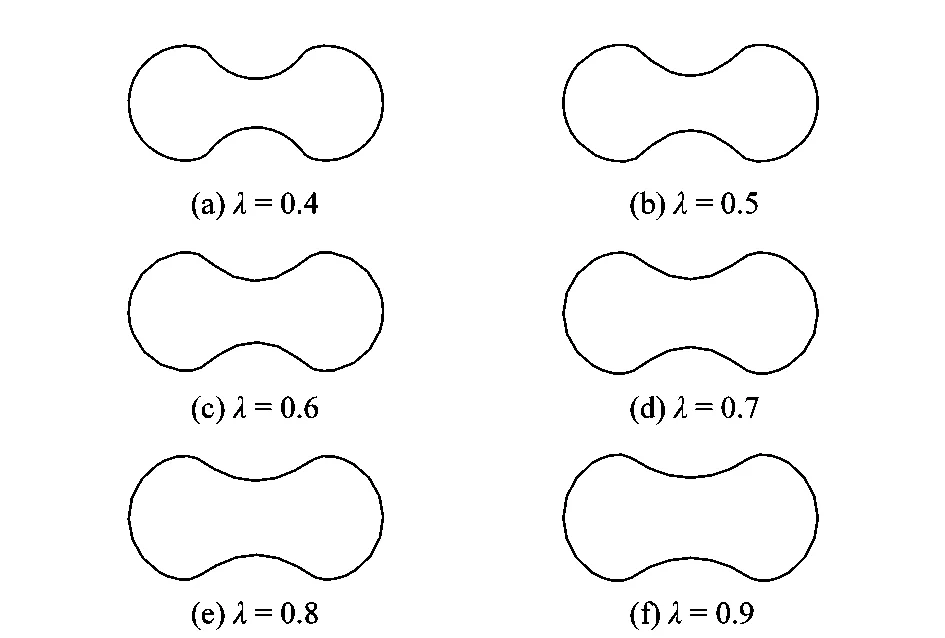
图5 不同椭圆率下的转子型线Figure 5 Rotor profile under different ellipticity

3 椭圆旋轮线型转子型线性能分析

转子在运转过程中，1个转子每转动1/Z周，1个腔室的气体就从罗茨泵进口输送到了罗茨泵出口，当转子旋转1周时，即完成1个周期的气体输送工作。该运转过程反映了罗茨泵的性能，通常该性能以容积效率[14]来量化。所谓容积效率是指罗茨泵在抽气过程中所输送的实际气体体积除以泵整个腔室的体积。同时因为罗茨泵的整个转子在轴的方向上形状完全一致，所以理论上罗茨泵的容积效率只与转子的端面形状相关，与其他因素关系不大。为了计算罗茨泵的容积效率更加方便，可以将容积效率的三维问题换算成二维问题。图6即为1个2叶罗茨泵的腔室横截面。阴影部分即为转子的腔室部分，根据图形可以得到转子的容积效率公式为：

图6 2叶转子的腔室横截面Figure 6 Cross section of chamber of 2-blade rotor

(11)

式中S为单个转子的面积。

根据转子型线的方程，可以得到转子型线的所有直角坐标，并将直角坐标换算成极坐标，对应函数为ρ=g(β)，ρ为极径，β为极径对应的角度，所以转子的面积公式为:

(12)

容积效率作为罗茨泵性能的重要参考之一，因此，为了验证新型转子型线的性能优劣，就椭圆旋轮线转子型线的不同参数对容积效率的影响进行了分析。根据椭圆旋轮线型转子型线的数学模型，转子型线的形状主要受椭圆率λ和转子叶数Z这2个参数的影响。为了准确地分析不同参数对转子型线容积效率的影响规律，采用唯一变量原则，即控制唯一变量而排除其他因素的干扰从而验证唯一变量的作用。

为了分析不同椭圆率对容积效率的影响规律，需限定转子型线的齿顶圆半径一定，即保证各个转子的大小一样；同时保证转子叶数相同，即保证各个转子形状一样。取齿顶圆半径为60 mm，转子叶数为2叶，不同椭圆率下椭圆旋轮线型线容积效率如表2所示。

根据表2所示数据，当椭圆率不断变小，转子的面积也越来越小，转子的容积效率越来越大。当椭圆率为0.4时，转子的容积效率最大，为0.665 6。

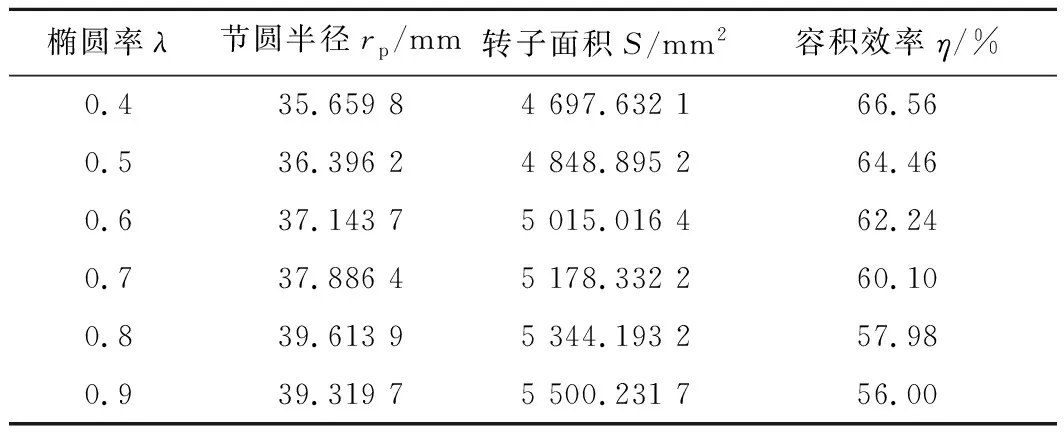
表2 不同椭圆率下罗茨泵的容积效率

传统摆线转子受摆线形成原理的限制，节圆半径和齿顶圆半径比值固定，转子齿顶圆半径和节圆半径的比值即径距比固定，2叶摆线转子型线径距比固定为1.5，取齿顶圆半径为60 mm，计算得到2叶摆线型转子的容积效率如表3所示。可知摆线型转子型线的容积效率小于椭圆旋轮线型转子型线。

表3 摆线型转子参数

根据表2和表3所示数据分析，椭圆旋轮线型转子容积效率均大于摆线型转子，当椭圆率为0.4时其容积效率相比摆线转子最大容积效率0.540 9提高了约23.09%。

对圆弧型转子设计时，圆弧型转子型线径距比不固定，2叶圆弧型转子型线径距比的取值范围为1.236 8～1.669 8。同样对圆弧型转子容积效率分析时，参照唯一变量原则，取齿顶圆半径为60 mm，取不同径距比分别为1.300 0，1.400 0，1.500 0和1.600 0，圆弧型转子相对应参数如表4所示。

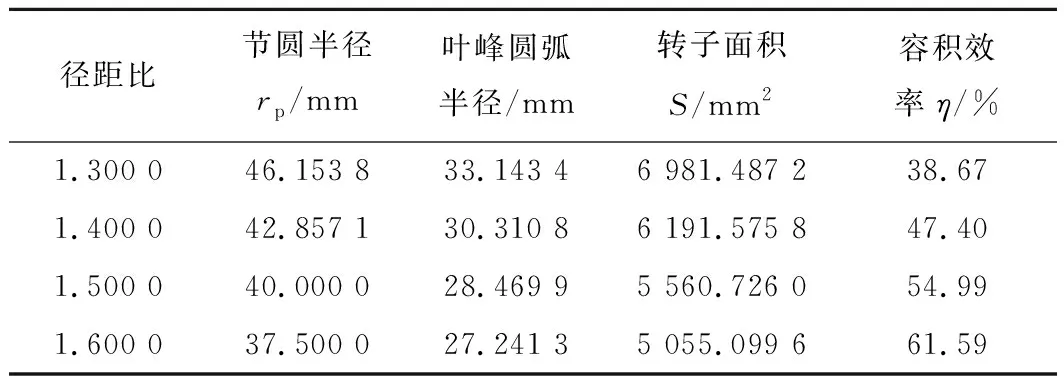
表4 圆弧型转子参数

根据表2、表3和表4所示的数据分析，当圆弧型转子的径距比变大到1.5时，圆弧型转子容积效率与摆线型转子容积效率基本一样，当径距比继续变大时，圆弧型转子容积效率超过摆线型转子。椭圆旋轮线型转子的椭圆率在0.6以下时，椭圆旋轮线型转子的容积效率比圆弧型转子大，当椭圆率为0.4时，其容积效率相比圆弧转子最大容积效率61.59%，提高了约8.07%。当椭圆旋轮线型转子型线椭圆率在0.6以下时，转子的容积效率最高，比传统罗茨泵转子型线更有优势。

4 结论

课题组提出了一种新型的椭圆旋轮线转子型线，推导其数学模型。对于齿顶圆半径为60 mm，转子叶数为2叶的罗茨泵转子，在不发生根切的情况下，椭圆率与转子的容积利用率大小成反比。当椭圆率为0.4时，椭圆旋轮线型线容积效率最大，达到66.56%，相比于传统摆线型和圆弧型转子，容积效率分别提高了23.09%和8.07%，说明椭圆旋轮线型线在性能方面比传统摆线型与圆弧形转子型线更有优势。现有的改善是直接对转子型线的改善，后续可以运用NURBS曲线直接表达旋转的椭圆，通过曲线局部可调性进一步优化转子型线。