纳入裂尖位置实时预测的天然气管道裂纹扩展模拟方法

甄 莹，常 群，曹宇光，祖毅真，钮瑞艳

(1.中国石油大学(华东)储运与建筑工程学院，山东青岛 266580；2.中国石油大学(华东)山东省油气储运安全重点实验室，山东青岛 266580)

延性断裂作为制约高钢级天然气管道发展的瓶颈问题[1-3]，亟需对其开展深入研究。全尺寸爆破试验作为最可靠的研究方法，因受其试验费用、周期及难度等方面的限制而无法广泛开展[4]，数值模拟方法成为协助其开展相关研究的有效手段。管道裂纹扩展过程较为复杂[5-11]，使用基于全尺寸爆破试验数据拟合的气体减压模型结合成熟损伤断裂模型的有限元技术可以简化该过程中气体减压与结构变形间复杂的流固耦合[8,12-14]，在计算难度与效率方面具有较大的优势，但仍需解决几个问题。一是选择高效且准确的损伤断裂模型来实现裂纹动态扩展过程的模拟,二是复杂加载的实现。随着裂纹不断扩展，以裂尖为分界的内压分布变化必然引起边界条件的连续变化，而重新定义每次增量的压力分布是不切实际的[15- 16]，目前并未形成较好的处理方法。针对这些问题，笔者选用在断裂韧性表征方面较为优越的GTN模型，通过归纳大量全尺寸管道爆破试验数据，提出管道裂纹扩展过程中裂尖位置随加载时间分阶段近线性变化的基本假设，根据该假设构建纳入裂尖位置实时预测的迭代加载法；在此基础上建立全尺寸管道有限元模型，结合气体减压模型及所提出的加载法对X80管道裂纹动态扩展过程进行模拟，并利用全尺寸爆破试验数据对模型进行验证。

1 迭代加载法

使用气体减压模型的管道裂纹扩展模拟需要将管内加载区域分为裂尖前和裂尖后两个部分，随着裂纹不断扩展，以裂尖为分界的内压分布变化必然引起边界条件的连续变化。归纳了不同钢级、不同尺寸管道全尺寸爆破试验中裂尖位置随时间的变化规律[16-19]如图1所示。

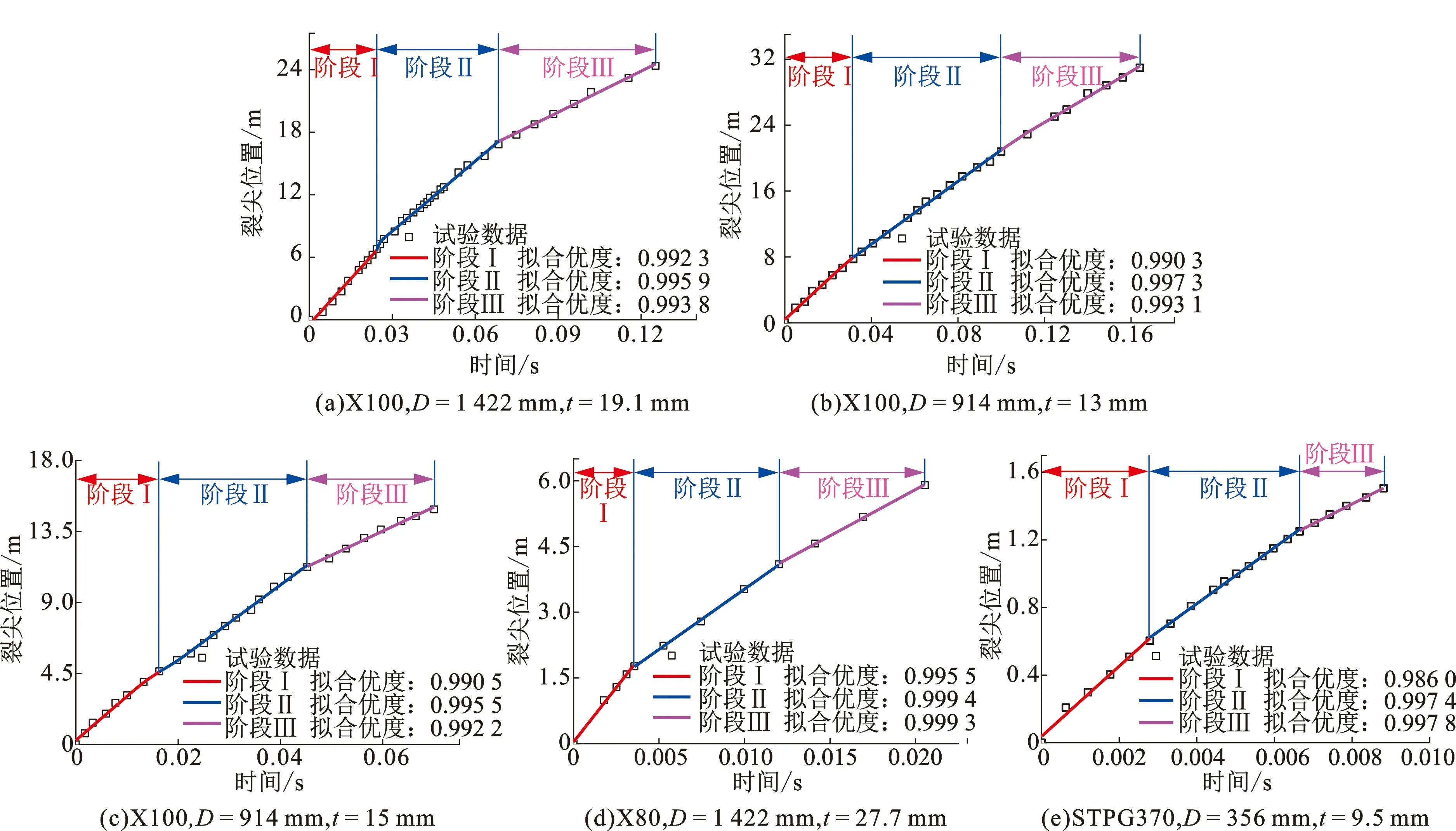
图1 全尺寸管道爆破试验数据及其分段线性拟合Fig.1 Experimental data of full-scale pipeline burst test and its piecewise linear fitting

由图1可知，不同管道裂尖位置均随时间呈近线性变化，为使全尺寸管道爆破试验数据集中的分布于线性拟合线附近，将整个裂纹扩展过程分为阶段Ⅰ、阶段Ⅱ及阶段Ⅲ，对3个阶段分别进行线性拟合(图1)。可见，所有试验数据基本位于拟合线上，拟合系数均大于0.99，说明在一定范围内裂尖位置基本随加载时间线性变化。因此提出管道裂纹动态扩展过程中裂尖位置随时间分阶段近似线性变化的基本假设。

根据上述假设，若管道裂纹扩展过程中扩展速度已知，则可近似得到裂尖位置随时间的变化关系；然而，实际管道爆破试验或管道断裂事故的裂纹扩展速度难以预测。同时由于裂纹起裂及止裂阶段线性规律并非严格满足，若将管道全程裂纹扩展速度设为定值，则会产生较大误差。因此提出一种纳入裂尖位置实时预测的迭代加载法(定义为CTPI method)：将整个裂纹扩展过程离散为几个阶段，每个阶段计算结束后，利用Python提取裂尖位置与时间数据并计算裂纹扩展速度，之后将裂尖位置表示为裂纹扩展速度与时间之函数关系，将此关系代入下一阶段加载子程序中作为加载的边界条件进行相应模拟。如此进行不同阶段模拟的迭代，直到计算完成或裂纹充分扩展，则可近似实现每个增量步中边界条件随裂尖位置的实时变化。

2 天然气管道裂纹动态扩展数值模拟

2.1 管道有限元模型

开展单轴拉伸与三点弯试验，以获得材料本构与GTN模型损伤参数，相关试验与参数标定见文献 [20]。之后根据试验所用管道尺寸(外径D为1 422 mm，壁厚t为27.7 mm)，考虑其对称性，建立四分之一模型，引入与管道外径尺寸相同的初始裂纹。为保证裂纹可以充分扩展，将管道轴向总长的一半设为6倍外径。考虑到GTN模型严重的网格依赖性，将损伤断裂过程区管壁厚度方向划分12层单元，单元高度设为0.25 mm，采用过渡网格技术对管道网格进行划分以实现单元密度沿轴向及环向的逐渐递减，以此缩短计算时间。

有限元模型轴向采用了两种不同尺寸的单元(轴向单元长度Le=0.5 mm和Le=1 mm)来研究网格尺寸效应。图2为Le=0.5 mm时对称显示为二分之一管道的有限元模型。将已标定的GTN损伤演化参数赋予管道断裂过程区，其余位置设置传统弹塑性材料参数。

2.2 基于纳入裂尖位置实时预测的迭代加载法载荷施加

Nonn等[19]提供了与本文所研究X80管道材料性能相似、尺寸相同的全尺寸管道爆破试验数据(图1(d))，依据该试验工况对管道进行加载，并以试验数据验证模型可靠性。考虑模型的对称性，在管道四分之一模型靠近初始裂纹一端施加z方向的对称约束，轴向施加y方向的对称约束，同时管道另一端施加等效拉力模拟端盖效应。

图2 全尺寸管道有限元模型Fig.2 Finite element model of full-scale pipeline

图3 二维指数型气体减压模型Fig.3 2D exponential gas decompression model

利用提出的纳入裂尖位置实时预测的迭代加载法对管道内部进行加载，将管道变形路径划分为多个阶段，在初始阶段以原始裂尖位置作为加载的边界，借助Fortran语言编写VDLOAD子程序，将加载区域分为裂尖前与裂尖后两个区域。裂尖前根据试验管道设计系数0.72及模拟所用材料本构参数，确定初始压力为16.38 MPa，加载过程中该数值在20 ms内线性下降至初始水平p0的40%；裂尖后选用忽略压力沿环向变化的二维指数型气体减压模型对管道进行加载(图3)。初始模拟完成后，利用Python提取裂纹扩展速度，并将裂尖位置表示为裂纹扩展速度与加载时间之函数关系，将此函数代入下一阶段VDLOAD加载子程序中，以此预测新的裂尖位置并将其作为裂尖前后两个加载区域的分界点。由于所代入的裂尖位置函数与时间相关，因此加载过程中边界条件实时更新，如此进行不同阶段模拟的迭代，直到计算完成或裂纹充分扩展。上述管道的边界条件及载荷施加的示意图如图4所示。

图4 管道模型边界条件及载荷示意图Fig.4 Schematic diagram of boundary conditions and load for pipeline model

3 天然气管道裂纹动态扩展数值模拟结果

将管道裂尖位置和速度历史的数值结果与X80管道全尺寸爆破试验[19]的试验结果进行对比，如图5所示。可见，借助本文提出的迭代加载法，两种单元有限元模型所得管道裂尖位置随时间的变化基本吻合，与试验结果趋势一致，最大误差约为10%，可以认为满足工程需求。

由图5可以看出，随时间增加，两模型裂纹扩展长度增加均变缓，裂纹扩展速度均随之出现下降趋势，即管道趋于止裂。Le为0.5和1 mm的模型结果差别较小，证明在当前网格划分策略下模拟结果对网格不敏感，模型结果与试验结果趋势一致，说明数值模型中假定的气体减压与实际减压行为没有显著差异，也进一步证明了本文中所提出的纳入裂尖位置实时预测的迭代加载法可以实现边界条件的实时移动，近似实现了气体减压、管道变形与裂纹扩展的多场耦合。采用Le为0.5 mm的模型进行后续分析。

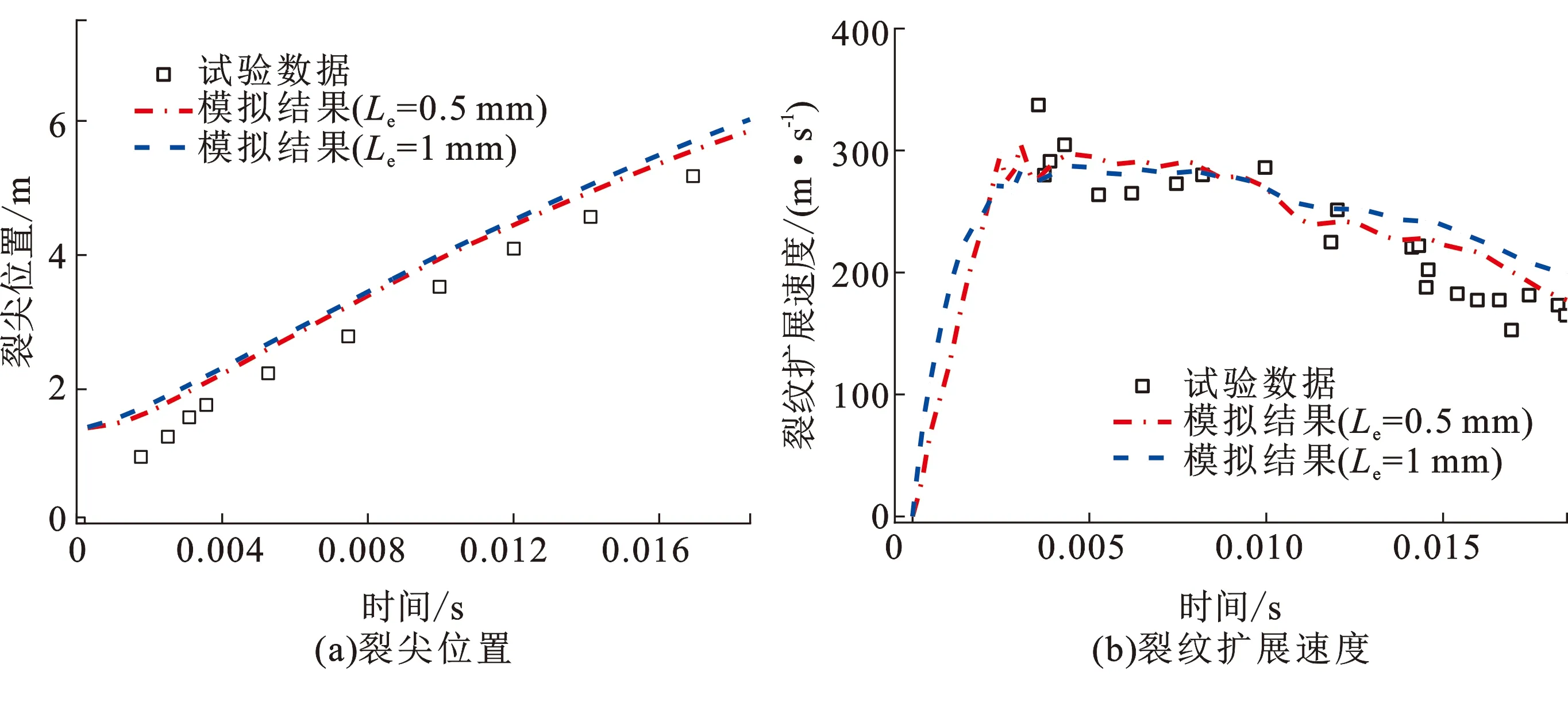
图5 试验与模拟结果对比Fig.5 Comparison of test and simulation results

为了进一步说明纳入裂尖位置实时预测的迭代加载法(CTPI method)的必要性，将该加载过程进行简化：同样采用分步迭代的加载方法，直接将上一步计算完成时的裂尖位置作为下一步加载的分界点，定义该方法为简化的迭代加载法(S-CTPI method)；同时考虑气体无减压的情况，即给管道施加均布压力，不考虑压力随时间与位置的变化，定义该方法为均布加载法(NGD method)。采用这3种加载方法对管道裂纹动态扩展过程进行模拟，将每一阶段预测并作为加载边界条件的裂尖位置与模拟所得实际裂尖位置随时间的变化关系汇总于图6。

为便于比较，将图6曲线划分为3个阶段。可见，第一阶段裂纹扩展速度逐渐加快，但时间较短，CTPI method与S-CTPI method数据吻合较好，但均布加载法NGD method所得裂纹扩展长度均大于上述两种方法。第二阶段裂纹位置变化与时间基本呈线性关系，该阶段裂纹扩展速度基本稳定，因此CTPI method与S-CTPI method均分两次迭代。从图6中可以看出，CTPI method中由前一阶段裂尖扩展速度预测并代入后一阶段压力分布计算的裂尖位置与实际模拟所得裂尖位置吻合程度极高；尽管S-CTPI method未考虑裂尖位置的连续变化，但仍得到了连续的模拟结果，且结果与考虑了加载边界实时变化的CTPI method基本吻合。不考虑气体减压的NGD method与两种迭代加载法模型数据也较为吻合。第三阶段较第二阶段时间短，但由于裂纹扩展速度不再保持定值，该阶段均分3次迭代。由图6可知，CTPI method模拟所得该阶段裂纹尖端位置变化曲线与稳定扩展阶段相比增速已明显下降，对应于图5中裂纹扩展速度下降阶段，该阶段预测并应用的裂尖位置与模拟所得裂尖位置仍然吻合，说明CTPI method可以有效模拟管道动态裂纹的止裂现象。S-CTPI method模拟所得裂尖位置仍保持与裂纹稳定扩展阶段一致的增速，裂纹扩展速度未下降，而未考虑气体减压的NGD method所得裂尖位置变化曲线斜率甚至呈现上升趋势。

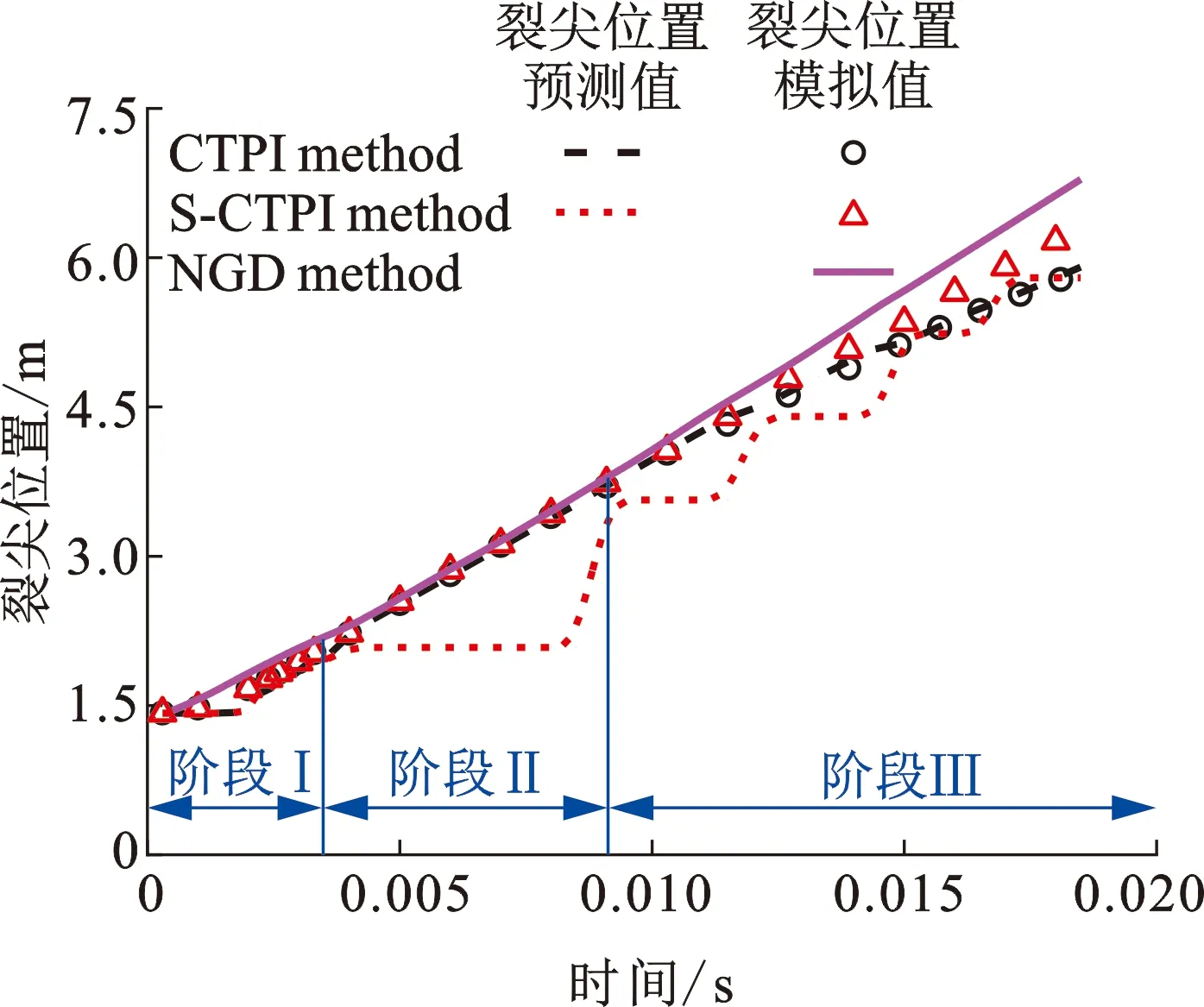
图6 不同加载方式下裂尖位置随时间变化Fig.6 Change of crack tip position with time under different loading methods

进一步计算3种加载方法所得裂纹扩展速度如图7所示。由图7可以看出，CTPI method所得裂纹扩展速度曲线最为平滑，而另外两种方法曲线均存在突变。CTPI method所得裂纹扩展速度在裂纹稳定扩展阶段内基本保持定值，而后随气体减压呈现下降趋势；S-CTPI method模拟所得裂纹扩展速度均在达到最大值后又在小范围内波动，未出现明显下降趋势；而未考虑气体减压的NGD method所得裂纹扩展速度呈现轻微上升趋势，这是由于裂纹扩展长度足够大，实际裂尖位置靠近管道末端，管道内压和等效轴向拉力共同作用使得裂纹扩展速度增加。数值方面，CTPI method、S-CTPI method和NGD method所得裂纹扩展速度稳态值或最大值依次增大。综上所述，本文中所提出的CTPI method可以有效模拟管道动态裂纹的止裂及气体减压过程，而S-CTPI method和未考虑气体减压的NGD method无法准确描述裂纹扩展速度的下降，因此无法有效实现管道止裂过程的模拟。

图7 不同加载方式下裂纹扩展速度随时间变化Fig.7 Change of crack velocity with time under different loading methods

图8 不同加载方式下管道塑性变形Fig.8 Plastic deformation of pipeline under different loading methods

模拟所得管道变形情况见图8。由图8可以看出，塑性变形主要集中于裂纹张开的襟翼上，在相同时刻，CTPI method、S-CTPI method及NGD method所得管道裂纹张开程度及裂纹附近塑性应变大于10%的区域依次增加。CTPI method所得变形图与实际管道试验更为接近，襟翼显示了移动的裂纹尖端后连续的“波浪”状变形；S-CTPI method所得管道裂纹张开程度较大，裂纹襟翼上残余了大量塑性变形，这是由于模型加载子程序中使用的作为加载边界的裂纹尖端位置未能实现实时移动，加载边界位于实际裂尖后某位置处，使部分管道未能遵循气体减压模型的压力递减规律而长时间承受较大内压；未考虑气体减压的NGD method模拟所得管道变形最大，裂尖后整个区域发生了完全屈服，管壁张开程度超过180°，当加载时间达到0.018 s时，管壁发生了严重畸变，已不具备参考价值。由此可知，若不考虑气体减压则无法有效实现管道裂纹扩展的有效模拟。

4 管道裂纹动态扩展模拟方法

4.1 迭代次数影响

不同迭代次数时模拟所得裂尖位置变化曲线见图9。由图9可以看出，在每个迭代步内，由前一阶段预测并嵌入加载子程序作为加载分界点的裂尖位置与模拟所得实际裂尖位置之差由零逐渐增加，在该迭代步结束时达到最大。对于五次迭代情况，该差值整体较小，最大仅为0.15 m，证明加载与实际情况吻合较好；对于二次迭代情况，在高压力水平下该差值最大为0.8 m，在低压力水平下最大为0.23 m；而且裂尖位置预测值始终大于模拟值，导致裂尖处及裂尖后部分位置位于减压区，使得所受压力小于实际情况而开裂压力减小，从而使裂纹扩展速度过早下降。

图9 迭代次数对裂尖位置影响Fig.9 Effect of iteration number on crack tip position

图10为不同迭代次数时由前一阶段预测并嵌入加载子程序作为加载分界点的裂尖位置与模拟所得实际裂尖位置之差。由图10可以看出，迭代次数越少，该差值最大值越大。图11为迭代次数对裂纹扩展速度的影响。由图11可以看出，迭代次数对初始阶段和稳定裂纹扩展阶段的裂纹速度影响不大。对于第三阶段，迭代次数越少，裂纹速度下降越明显。对于本文模拟工况，当迭代次数达到四次时，模拟结果趋于稳定，且不随迭代次数增加而变化。

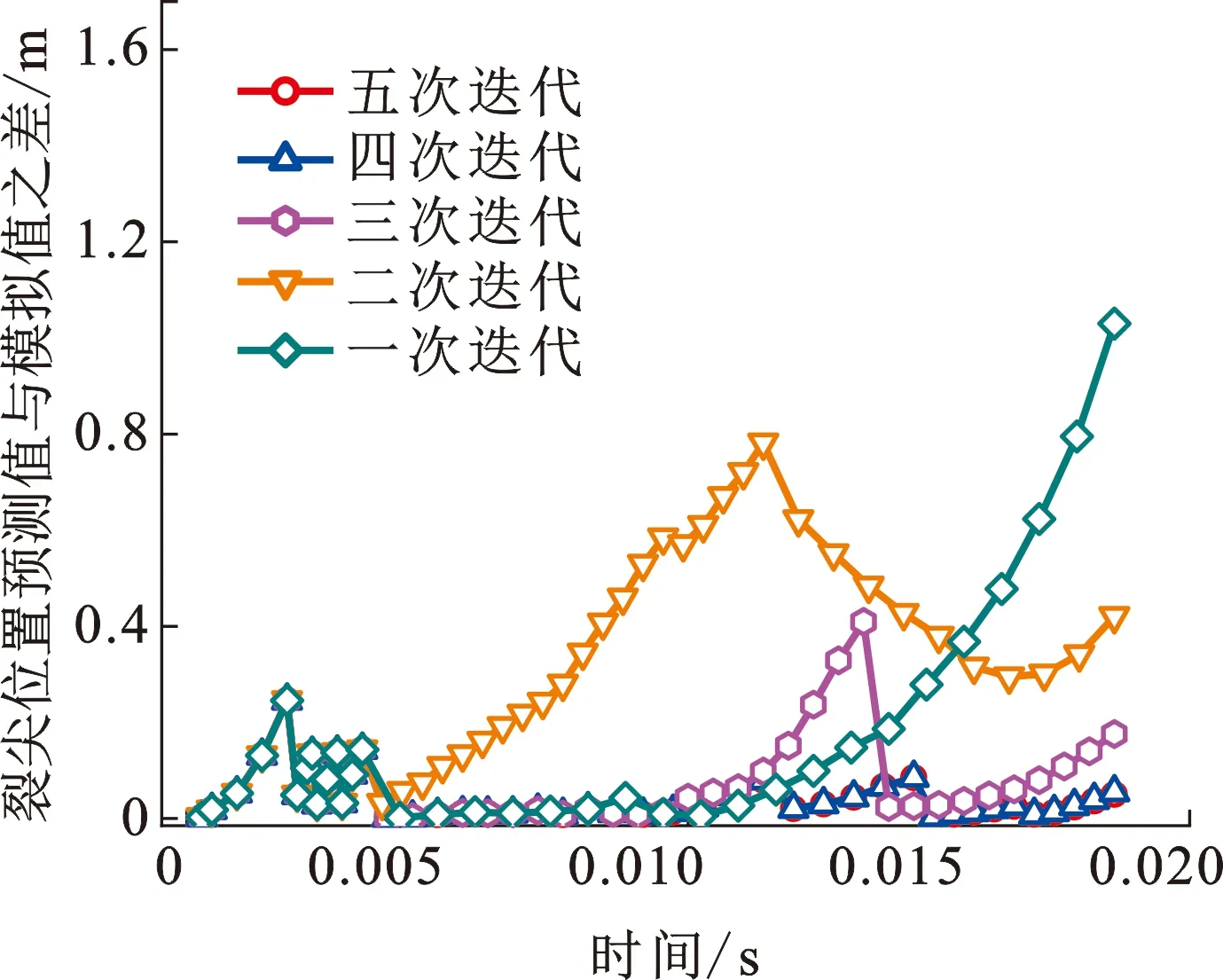
图10 迭代次数对裂尖位置预测值与模拟值之差影响Fig.10 Effect of iteration number on differences between predicted and simulated crack tip position

图11 迭代次数对裂纹扩展速度影响Fig.11 Effect of iteration number on crack velocity

4.2 气体减压模型

气体减压模型为对现有为数不多的真实管道爆破试验数据和前人数值计算结果的简化与近似。使用的气体减压模型主要包括二维指数型(图3)、二维线性(图12)、三维指数型(图13)3种，图14为3种模型模拟所得裂尖位置与裂纹扩展速度。

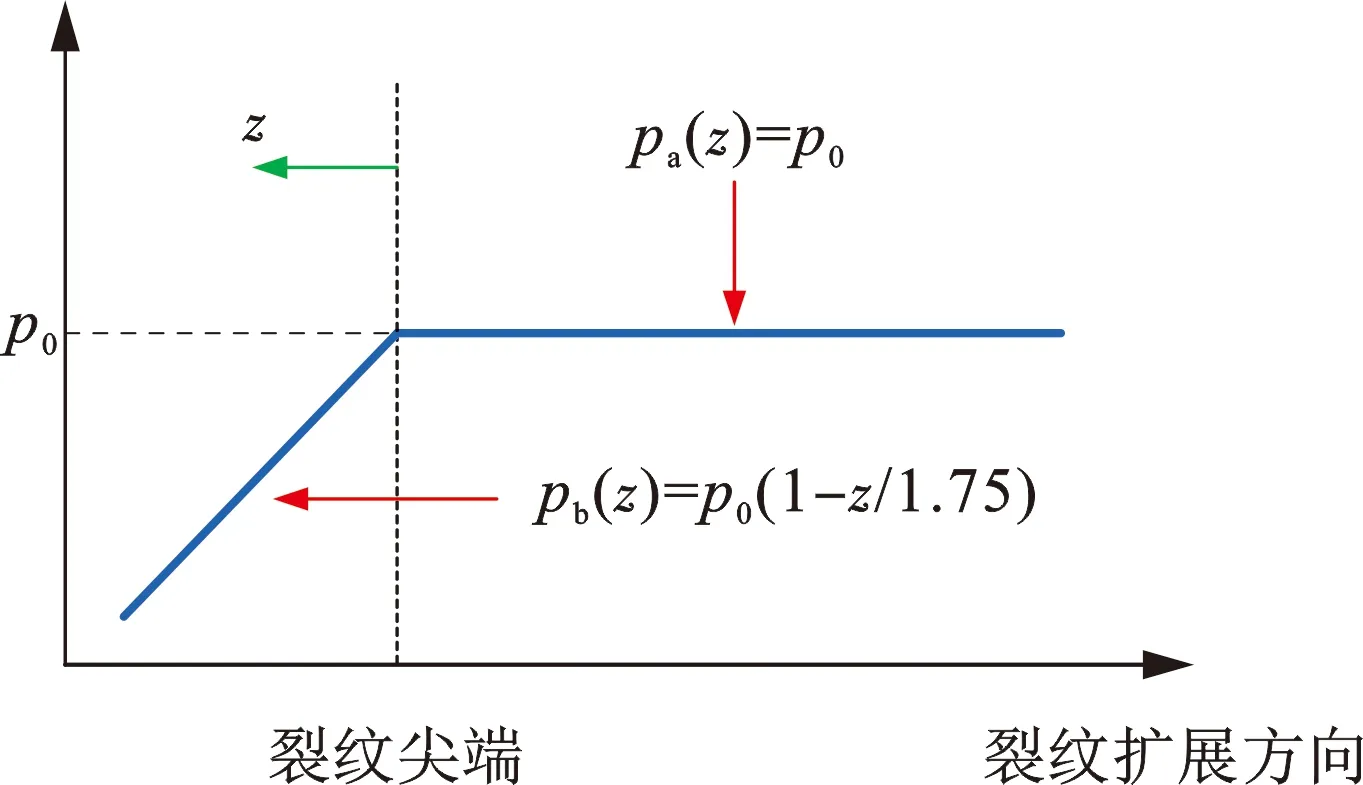
图12 二维线性气体减压模型Fig.12 2D linear gas decompression model

图13 三维指数型气体减压模型Fig.13 3D exponential gas decompression model

由图14可以看出，两种指数型模型模拟所得结果在整个裂纹扩展阶段表现出良好的一致性，曲线基本重合；二维线性模型所得数据在裂纹稳定扩展阶段中期之前与两种指数型模型吻合较好，但随着持续加载，其模拟所得裂尖位置仍保持近似线性增长的趋势，裂纹扩展速度也并未下降。说明在管道动态裂纹扩展模拟过程中，3种模型不可以相互替代，在相同压力水平及其他设置下，线性模型所得裂纹扩展速度要大于其他两种模型，所得止裂长度也会更大，将其用于止裂设计研究可能会出现非保守的结果。

图14 气体减压模型对裂尖位置和裂纹扩展速度影响Fig.14 Effect of gas decompression model on crack tip position and crack velocity

图15为不同气体减压模型模拟所得管道塑性变形情况。由图15可以看出，在当前压力水平下，二维与三维指数型模型所得管道变形与塑性分布情况几乎一致，二维线性模型得到了较大的裂纹开口，裂纹尖端周围塑性应变大于10%的区域也明显大于两种指数型模型。3种气体减压模型均实现了裂纹尖端后“波浪”状变形的模拟，其中二维线性模拟所得“波浪”变形更为密集，说明其轴向拉伸效应更显著。二维与三维指数型模型所得裂纹扩展长度、扩展速度、管道变形及塑性应变分布情况均一致，因此二者相互替代，考虑模型形式更为简单，推荐使用二维指数型气体减压模型对管道动态裂纹扩展进行模拟。

图15 气体减压模型对管道塑性变形的影响Fig.15 Effect of gas decompression model on plastic deformation of pipeline

5 结 论

(1)纳入裂尖位置实时预测的迭代加载法可有效实现裂纹扩展过程中加载边界的实时移动，近似实现了气体减压、管道变形与裂纹扩展的多场耦合，可以有效反应管内气体分布情况及其随裂尖移动的实时更新;应用该方法可有效实现裂纹扩展及止裂模拟，所得管道断裂参量、裂纹张开程度及裂纹尖端后典型的连续的“波浪”状变形与实际管道试验结果类似。

(2)纳入裂尖位置实时预测的迭代加载法一定程度上依赖于迭代次数，在每个迭代步内，由前一步预测并嵌于加载子程序作为加载分界点的裂尖位置与模拟所得实际裂尖位置之差由零逐渐增加，在该迭代步结束时达到最大；理论上讲，迭代次数越多，模拟越接近实际情况。

(3)二维与三维指数型气体减压模型模拟所得裂纹扩展长度、速度、管道变形均较为一致，二者可以相互替代，考虑二维模型形式较为简洁，推荐将其用于后续天然气管道裂纹动态扩展的模拟。