多脊PDC切削齿破岩有限元仿真及其几何结构影响

王新锐,张 辉,张矿生,欧阳勇,于 洋,刘 彪,刘科柔,陈雨飞

(1.中国石油大学(北京)石油工程学院,北京 102249;2.中国石油长庆油田公司油气工艺研究院,陕西西安710018;3.低渗透油气田勘探开发国家工程实验室,陕西西安710018;4.中国石化西北油田分公司石油工程技术研究院,新疆乌鲁木齐 830011)

PDC钻头依靠高钻速、长进尺、低风险等优势,已经成为钻进深井、超深井的首要选择[1-2],同时深部地层岩石非均质性强、难吃入等特点也制约了其破岩效率[3]。近来出现了多种不规则几何形状的切削齿,其中多条脊结构的多脊齿在现场提速效果显著。Alawi等[4]介绍了斧形齿(二脊)在厚砾岩地层中的使用情况,二条脊的结构使扭矩波动降低,机械比能降低,从2.6趟钻钻穿砾岩层降至1.3趟钻;李乾等[5]介绍了斧形齿钻头在东海深部地层提速超过15%,出井磨损轻微。试验研究方面,邹德永等[6]设计了锥型齿混合钻头,发现只有当岩石硬度及钻压高过某一值时,锥形齿钻头的表现才优于常规钻头;Xiong等[7]对锥形齿破岩机制进行了研究,发现锥形齿的切削力比平面齿低46.14%,破岩体积比平面齿小且存在拉伸破坏;Shao等[8]通过VTL试验发现二条脊的几何形状是影响其破岩效率及抗冲击性的主要因素。数值模拟方面,Yang等[9]研究了PDC齿切向及横向双向切削岩石的破岩机制,发现横向切削会产生拉应力,破坏形式主要是脆性断裂和剪切破坏;吴泽兵等[10]对牙轮-PDC混合钻头进行了研究,发现牙轮主导混合钻头适用于硬地层,PDC主导混合钻头适用于软地层;Zeng等[11]对比了三脊齿与平面齿的切削力变化规律,并强调了多脊齿脊角对破岩效率存在影响;Chen等[12]研究了楔形齿的切削力及破岩体积,并优化设计出一种复合单牙轮钻头;赵润琦等[13]模拟了斧形齿线性切削砂岩,发现斧形齿切削力波动小,机械比能低。大量成果证明有限元模拟得到的机械比能是准确的,笔者利用有限元软件显式分析模块,研究不同几何形状的多脊齿破岩效率。

1 有限元模型

1.1 多脊齿结构

目前多脊齿的聚晶金刚石层(PDC层)厚度一般为1～4 mm,由脊最高处延伸至齿边缘,从而在破岩时利用集中载荷破碎岩石,如斧形齿、奔驰齿、忍者齿等。简单的斧形齿、四脊齿结构如图1所示。其中d为切削齿直径,H为脊高,α为脊角,除了斧形齿外,多脊齿都存在脊后角γ,且一般都小于25°,四者存在一定的几何关系。

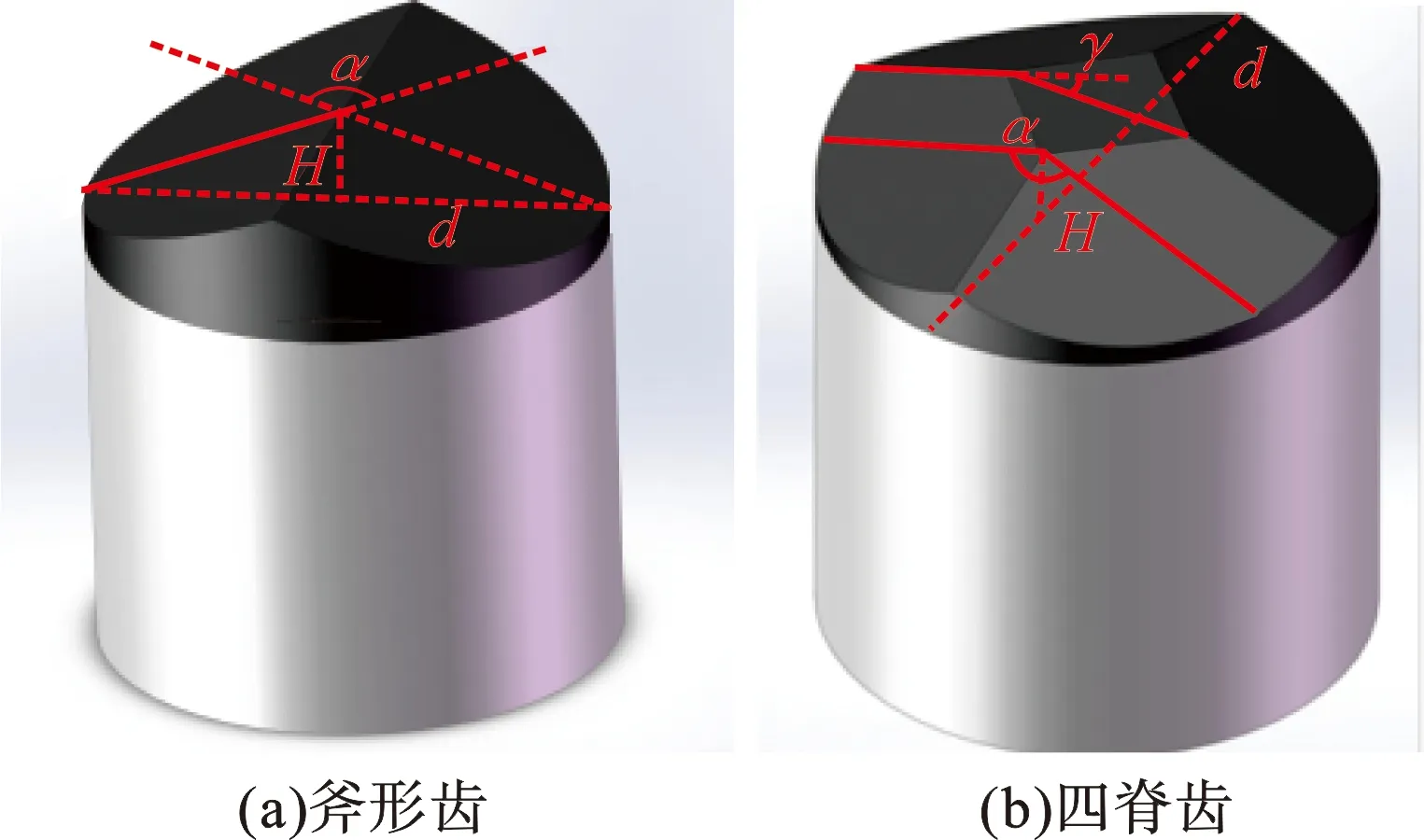
图1 斧形齿和四脊齿模型示意图Fig.1 Diagram of axe cutter and 4-ridged cutter

本文中主要讨论多脊齿几何形状对破岩效率的影响,切削齿直径统一为15.88 mm。在破岩时脊角起到主导作用,多脊齿脊后角固定为15°～25°,改变脊角α以探究不同结构参数的多脊齿的破岩规律,具体几何参数如表1所示。

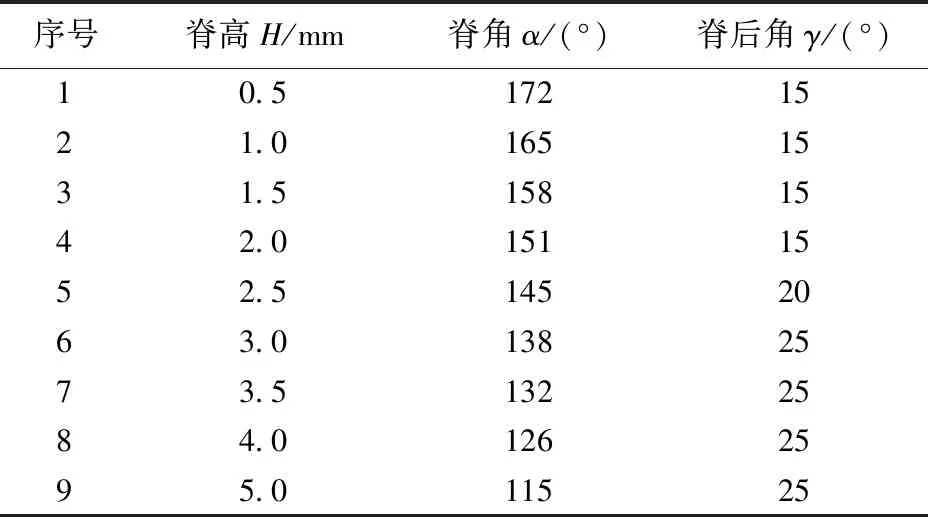
表1 多脊齿几何参数Table 1 Geometric parameters of multi-ridged cutters

1.2 模型假设

有限元模型假设:①岩石表现为各向同性,为均质弹塑性体;②忽略岩石温度及孔隙压力,且不含微裂缝、层理结构、溶洞等特殊结构;③采用固定切削半径的旋转切削运动研究切削齿破岩过程,忽略切削齿磨损;④切削齿破碎岩石过程中切削面投影对称。

1.3 岩石强度准则及失效判据

考虑中间应力σ2作用及岩石剪胀现象的Drucker-Prager模型被广泛应用于岩石破坏数值模拟研究,试验获得的M-C准则数据可与D-P准则匹配[14],D-P准则表达式为

(1)

式中,t为考虑中间主应力对屈服面影响的偏应力,MPa;p为等效抗压应力,MPa;β为p-t空间屈服面上的斜率;c为材料黏聚力,MPa;q为等效米塞斯应力,MPa;K为塑性流动应力比,0.778≤K≤1,取K=1.0;r为第三偏应力分量,MPa;σc为单轴抗压强度，MPa。

模型采用Ductile damage中等效塑性应变作为岩石损伤的判据,并设定损伤演化,即当岩石等效塑性应变εpl等于失效塑性应变εfpl时[15],岩石失去承载能力,岩石单元删除。

1.4 岩石有限元模型验证

基于上述本构模型建立围压条件下岩石三轴抗压强度有限元数值模拟模型,选取岩石直径为50 mm,高度为100 mm,采用C3D8R网格,共计28 700个网格。基于花岗岩室内试验确定岩石力学参数,如表2所示。

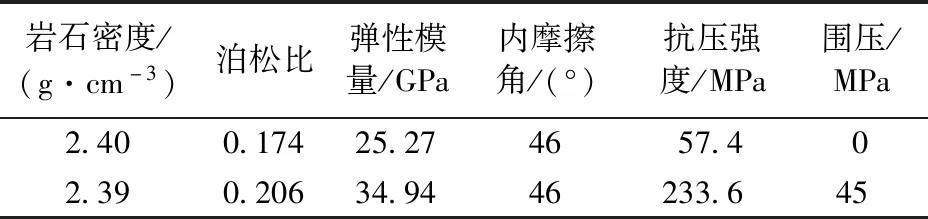
表2 花岗岩岩石力学特征参数Table 2 Mechanical characteristic parameters of granite

模拟过程中首先对岩样施加固定围压,计算出相应结果,然后对岩样底面添加完全固定边界条件,顶面添加刚体约束并施加载荷,花岗岩应力应变曲线如图2所示,最终失效时等效塑性应变如图3所示。围压为45 MPa时岩石应变及损伤形态与文献[16]中的试验研究结果拟合度较好,因此针对花岗岩所建立的岩石仿真模型可靠。

1.5 多脊齿与岩石相互作用有限元模型

对于给定机械钻速和转速的切削齿破岩模型,切削齿切削深度[17]可表达为

(2)

式中,dDOC为切削深度,mm;vROP为机械钻速,mm/min;N为转速,r/min;tmin为时间,min;h为切削齿进尺,mm;n为转数。

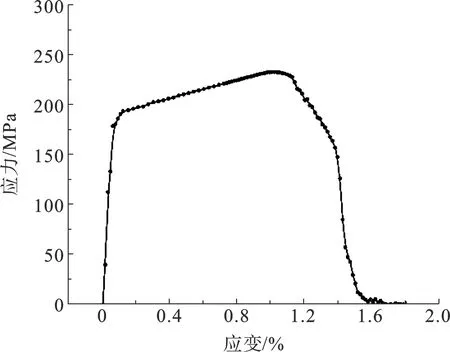
图2 岩石损伤仿真结果Fig.2 Rock damage simulation results

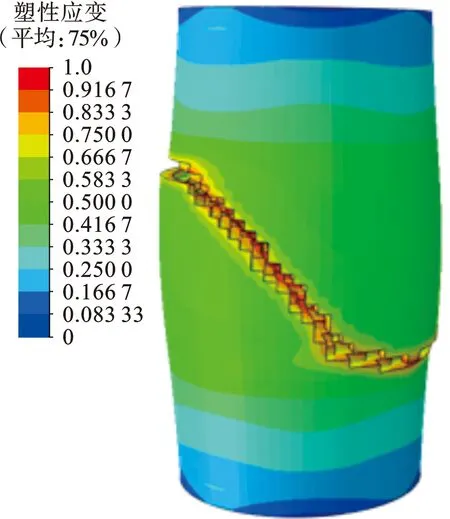
图3 三轴抗压强度仿真结果Fig.3 Simulation results of triaxial compressive strength test

模型设定切削齿进尺为2、4、6、8、10 mm,以固定速度逆时针旋转2周,无量纲分析步时间T设置为1,接触属性设定为罚,摩擦系数0.15,旋转第1周为压入并破碎岩石过程,切削深度逐渐增加,在切削齿转至第2周时吃入深度固定为1、2、3、4、5 mm。切削半径为28 mm,赵润琦等[13]通过数值模拟确定斧形齿最佳后倾角φ为15°～20°,故模型选定切削齿后倾角φ为15°。根据圣维南原理,岩样直径设定为100 mm、内径为20 mm、高度为20 mm,共372 160个C3D8R网格,岩样底面自由度设置为0,相互作用模型如图4所示。

1.6 机械比能计算方法

机械比能MSE是表征切削齿及钻头破岩效率的重要参数,其定义为破碎单位体积岩石所消耗的能量。在破碎相同岩石时,机械比能越小,破岩效率越高,MSE通常由工程参数中的钻压、扭矩、机械钻速、排量等参数获得[18]。模型破岩过程为切削齿先吃入岩石并旋转钻进,最终达到固定深度的进尺并停止破岩过程,因此需要考虑切向和轴向两个方面的机械能量消耗。本文中采用投影破碎面积计算机械比能,如图5所示,单个切削齿机械比能计算方程为

(3)

式中,ε为切削齿机械比能,J/mm3;W为破岩过程中切削齿做的功,J;V为岩石破碎体积,mm3;Ft为切削力,N;Fw为轴向力,N;At为切削齿横向破岩投影面积,mm2;Aw为切削齿轴向破岩投影面积,mm2。

图4 切削齿与岩石相互作用模型Fig.4 Mesh of cutter and rock interaction model

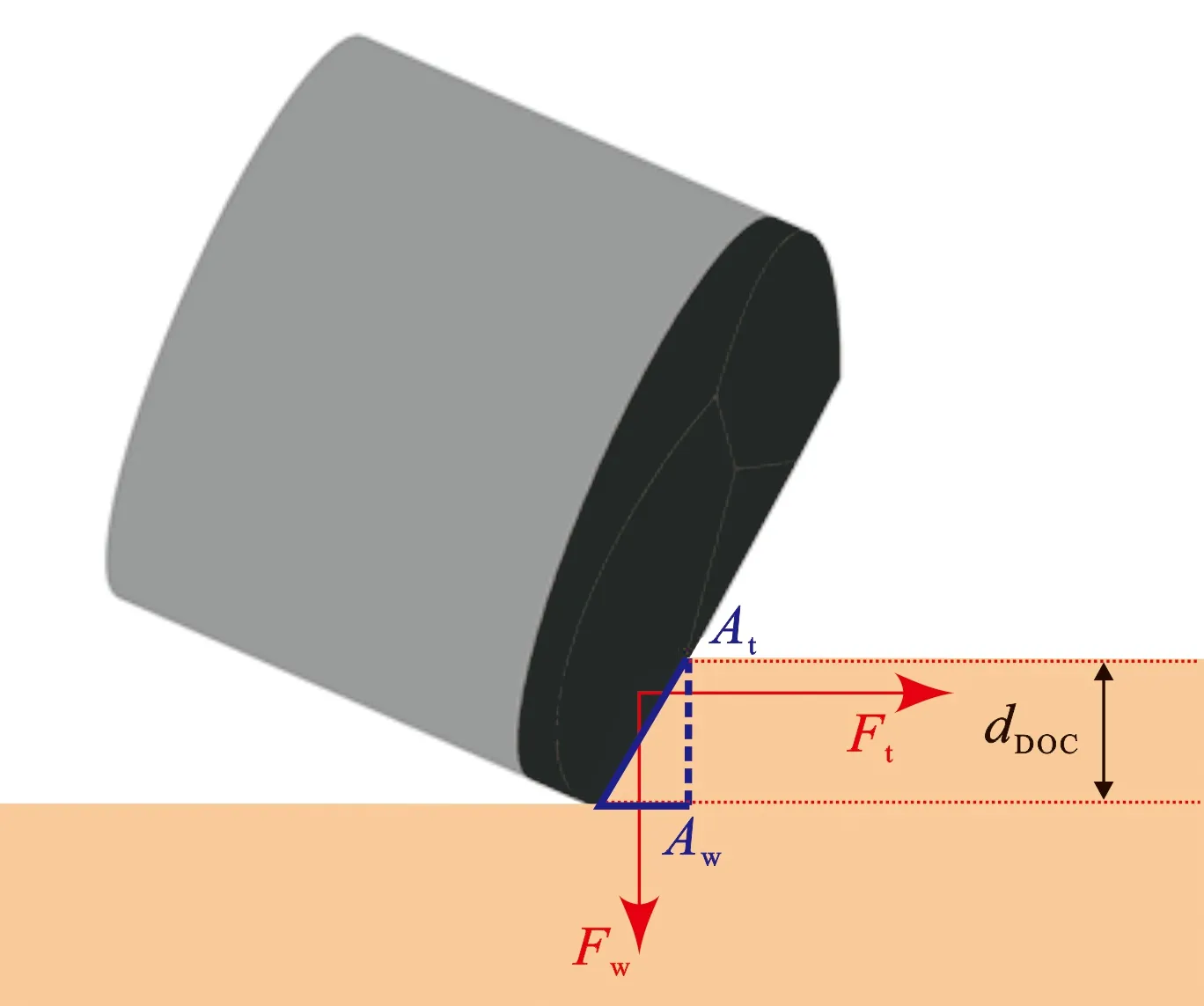
图5 多脊齿破岩受力分析Fig.5 Stress analysis of multi-ridged cutter in rock breaking

由于模型是旋转切削破岩,如图6所示,At为固定吃入深度时切削齿横向破岩投影面积,其计算公式为

(4)

其中

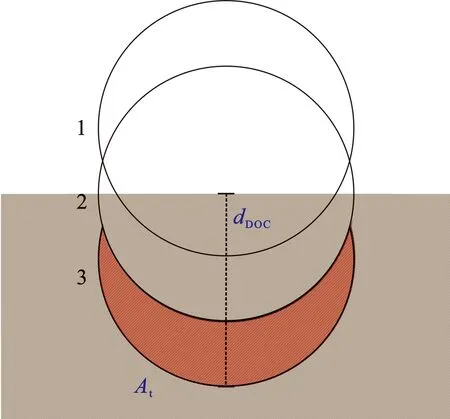
图6 切削齿破碎岩石投影面积Fig.6 Projected area of broken rock by cutters

单齿破岩过程中,随着切削深度的增加,切削齿破碎投影面呈月牙状,切削齿直径为15.8 mm,吃入深度1、2、3、4、5 mm对应的破岩投影面积分别为15.86、31.67、47.32、62.79、77.96 mm2。

计算机械比能考虑破岩时轴向力的作用,由于切削齿没有磨损且存在后倾角φ,因此几乎所有钻压由未破坏的岩石表面承受,如图5所示,在垂直面上的投影面积为Aw,计算公式为

Aw=Attanφ.

(5)

模拟为理想状态下的单齿切削,实际钻头破岩过程切削齿破岩投影面积由布齿密度决定,一般小于本模型的理论值,这将导致切削力与轴向力减小,但两者比值依旧为实际机械比能。

2 数值模拟结果

2.1 脊角对相互作用力的影响

多脊齿脊角是影响切削破岩过程中集中载荷及其分布关键的因素之一,图7为脊角151°、切削深度2 mm时斧形齿作用力。

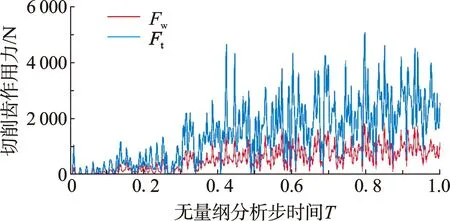
图7 多脊齿破岩切削力与轴向力变化Fig.7 Variation of cutting force and axial force of multi-ridged cutter in rock breaking

当T=0～0.5时为切削齿逐步吃入地层并旋转破岩的过程,切削力及轴向力随着切削深度的增加而增加,吃入过程切削齿平均切削力为774 N,轴向力为276 N;T=0.5～1时为切削齿以固定切削深度旋转破岩过程,切削力与轴向力的振幅趋于定值,此阶段平均切削力为2 157 N,平均轴向力为796 N。数值模拟结果与Shao等[8]的斧形齿破岩试验结果相近,进一步说明建立的数值模型可靠。

建立表1中的四脊齿模型进行旋转破岩模拟,T=0.5～1、切削深度为2 mm时四脊齿切削力Fs和轴向力Fn如图8所示。箱图中脊角180°为平面齿,有色框图为作用力25%～75%分位数的范围,上下线段为极值,黑圆点为力的平均值。结果表明切削深度固定为2 mm时,常用的脊角为165°的多脊齿切削力与轴向力显著小于平面齿,说明多脊齿扭矩更易控制,能够提供更平稳的钻进过程。随着脊角变小,多脊齿切削结构更加尖锐,破碎岩石的切削力不断减小,波动幅度也不断缩小,脊角165°时平均切削力为2 202 N,相较平面齿的2 855 N减小了22.9%。结果表明,多脊齿的脊角越小切削力越小,可能由于几何形状的尖锐化,切削齿尖端更易形成拉应力,但更尖锐的几何结构往往影响切削齿寿命,因此多脊齿的最佳脊角需要进一步分析讨论。

图8 不同脊角多脊齿与平面齿固定切削深度破岩作用力Fig.8 Rock breaking stress of multi-ridged cutters and plane cutters with different ridge angles

切削过程中轴向力结果如图8(b)所示,脊角165°的多脊齿为624 N,相较平面齿减少了21.8%。相较于切削力,轴向力的变化更加稳定,当脊角小于151°后,轴向力变化幅度趋缓。

2.2 脊角对多脊齿吃入性能的影响

切削齿的吃入性能是面对极硬地层井底造型、钻进软硬夹层的关键性能[19]。以往研究中往往设定好固定切削深度再进行线性破岩[20],切削齿的吃入性能鲜被考虑。模拟在T=0～0.5段多脊齿由未接触岩石至逐步吃入岩石,最终达到设定切削深度的过程。不同脊角的多脊齿在吃入地层时切削力如图9(a)所示,脊角172°的多脊齿平均切削力为910 N,相较于平面齿的1 182 N减少了23.1%。不同脊角之间多脊齿平均切削力随着脊角的增加而减少,但脊角126°的齿平均切削力仅比172°脊角的1号齿小98 N,脊角变化带来切削力变化在吃入过程中不明显,总体上切削力变化幅度随脊角变小而减小。在模拟时输出了切削齿碳化钨基座的接触应力,发现在吃入及切削过程中接触应力为0,说明在切削齿无磨损的条件下,大部分摩擦及受力在金刚石层发生。吃入地层过程中轴向力的变化如图9(b)所示。吃入过程平均轴向力小于正常钻进时,这也是现场作业小钻压造型的过程,且轴向力极值与钻进过程轴向力75%分位数相近,说明全新的钻头在钻进均质性地层且当钻压固定时总能达到相对稳定的切削深度,从而获得相对平稳的钻速,刚下井钻头发生机械钻速快速振荡即说明钻头可能已经损坏也是此原因。图9(b)表明脊角与轴向力之间的关系为正相关,随着脊角变小,吃入地层所需轴向力降低,132°～158°时降幅趋缓。126°脊角的齿平均轴向力仅为196 N,最大轴向力为660 N,相较于平面齿减小约41%。综上可知几何形状越“尖锐”的多脊齿,吃入地层性能越强,在钻进软硬夹层或极硬地层使用多脊齿将取得更好的效果。

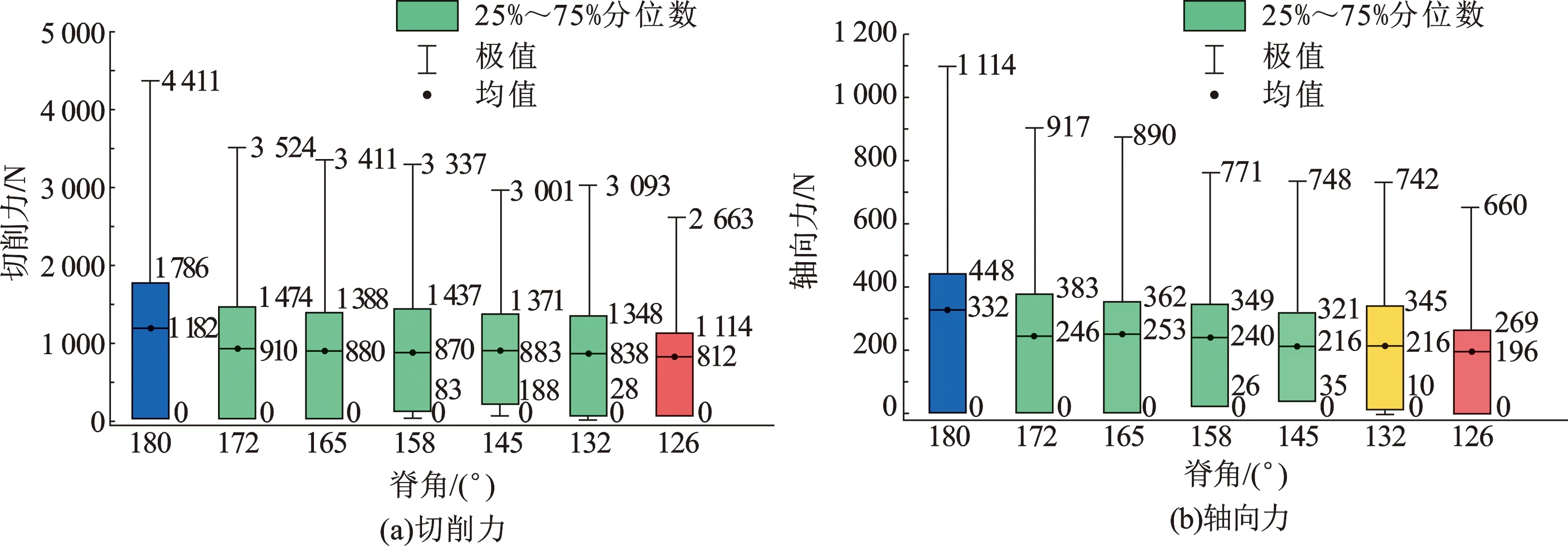
图9 不同脊角多脊齿与平面齿吃入地层作用力Fig.9 Penetrating formation stress of multi-ridged cutters and plane cutters with different ridge angles

2.3 脊角对机械比能的影响

利用上述数值模拟结果得到不同脊角多脊齿在2 mm切削深度时破碎岩石全过程的机械比能,如图10所示。首先平面齿机械比能相较于1号齿大18.7%,故多脊齿在破碎类似花岗岩等极硬岩石时存在一定优势。多脊齿机械比能随着脊角的变小而逐渐降低,在脊角138°～165°时机械比能降幅不大,但在115°～138°阶段快速下降。由于式(3)同时考虑了钻压和扭矩的两部分机械能量的计算,可知切削力变化幅度相较于轴向力来说相对较小,而脊角较小的多脊齿以较小的钻压获得更大的进尺,从而使机械比能变化趋势快速下降,但同时脊角较小的设计对多脊齿寿命及抗冲击性存在影响。

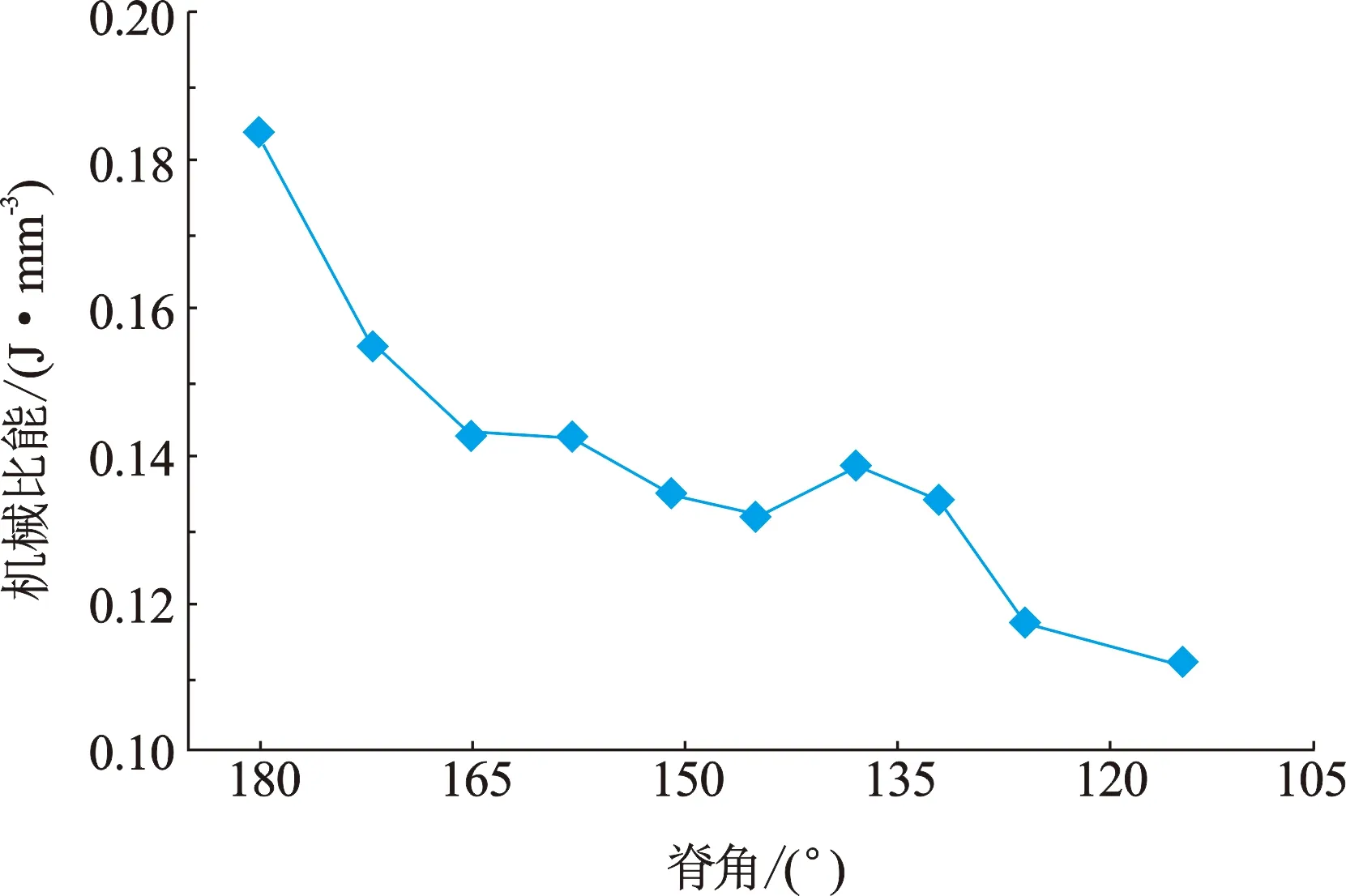
图10 不同脊角多脊齿2 mm切削深度时机械比能Fig.10 Mechanical specific energy(MSE)of multi-ridged cutters with different ridge angles and 2 mm cutting depth

2.4 吃入深度对机械比能的影响

选用脊角151°的4号四脊齿及脊角158°的3号三脊齿进行不同切削深度的机械比能变化规律研究,结果如图11所示，且图11(a)、12(a)中机械比能由不同切削深度条件下吃入地层的平均作用力计算得到。

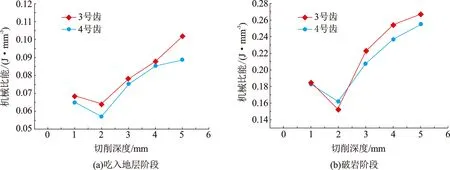
图11 多脊齿不同阶段机械比能Fig.11 MSE at varied stage of multi-ridged cutters

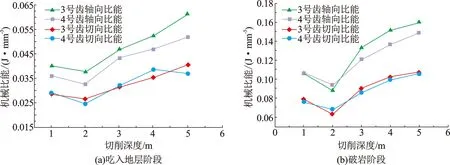
图12 不同阶段轴向切向机械比能Fig.12 Axial and tangential MSE at varied stage

在相同切削深度下,脊角小的4号齿机械比能略小于3号齿,且在吃入地层和破岩过程中二者均在切削深度为2 mm时达到最小机械比能。比较轴向及切向能耗结果发现,轴向比能在吃入地层阶段高于切向比能约40%,在破岩阶段高约30%,说明切向上的能量利用效率大于轴向上的,且能达到轴向的1.2～1.5倍(图12)。综上,多脊齿最优切削深度为2 mm,最优切削深度在钻头布齿设计中主要体现在前后排齿高度差的选择,虽然在钻进过程中钻压不能使钻头一直处于最优切削深度工作,但是合理的高度差能够保证钻头不过度吃入地层降低破岩效率且能够提高钻头寿命。

3 分析与讨论

前述研究发现脊高的增高导致几何形状更加尖锐的多脊齿更易破碎岩石,但尖锐的几何形状也会使多脊齿更易出现接触应力集中现象,如图13所示。

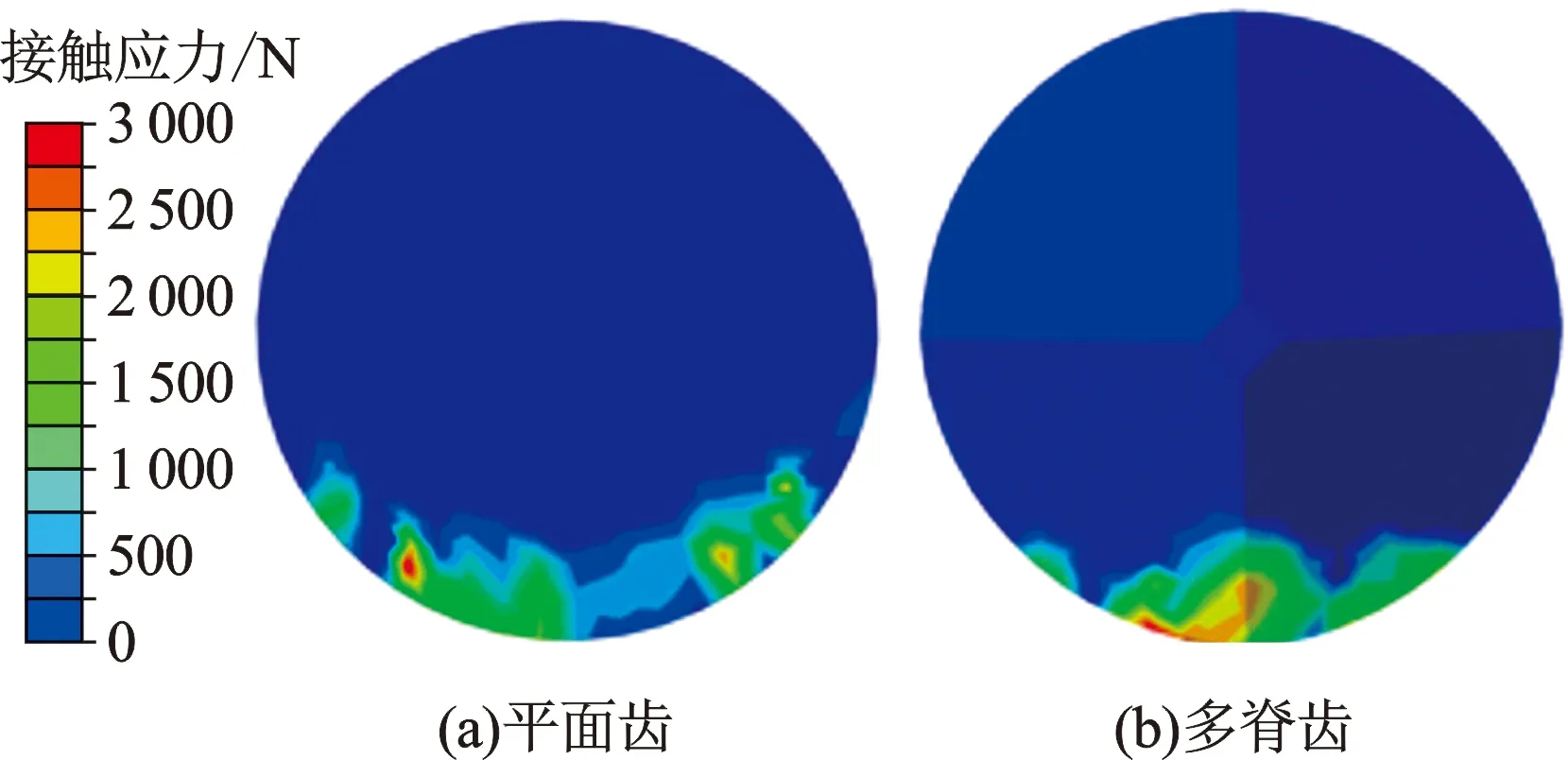
图13 数值模拟接触应力云图Fig.13 Cloud diagram of numerical simulation contact stress

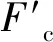
(6)

且当切削力Ft越大时Fs越大,钻头设计中不平衡力常以与形成不平衡力的力以比值的形式表示[21],故设定侧向力系数Kc,平面齿由于没有脊角,故侧向力系数可以忽略不计,

(7)

关于磨损情况的变化则复杂得多,一方面由于较小的脊角使齿尖端更易磨损,但脊高变高导致金刚石层变厚从而耐磨性及热稳定性更优,导致一种复杂磨损工况,因此本文中着重研究脊高、脊角和切削半径对多脊齿侧向力的影响。为了探究Fc与Fo间的差值,将多脊齿底部两侧表面设为积分输出截面,分别输出两表面的接触应力。结果表明,在半径为18 mm、切削深度为2 mm的切削过程中,侧向力系数Kc如图15(a)所示,利用非线性拟合处理数据,得到侧向力系数与脊高和脊角间的拟合公式为

Kc=7.08exp(H/2.74)-6.65.

(8)

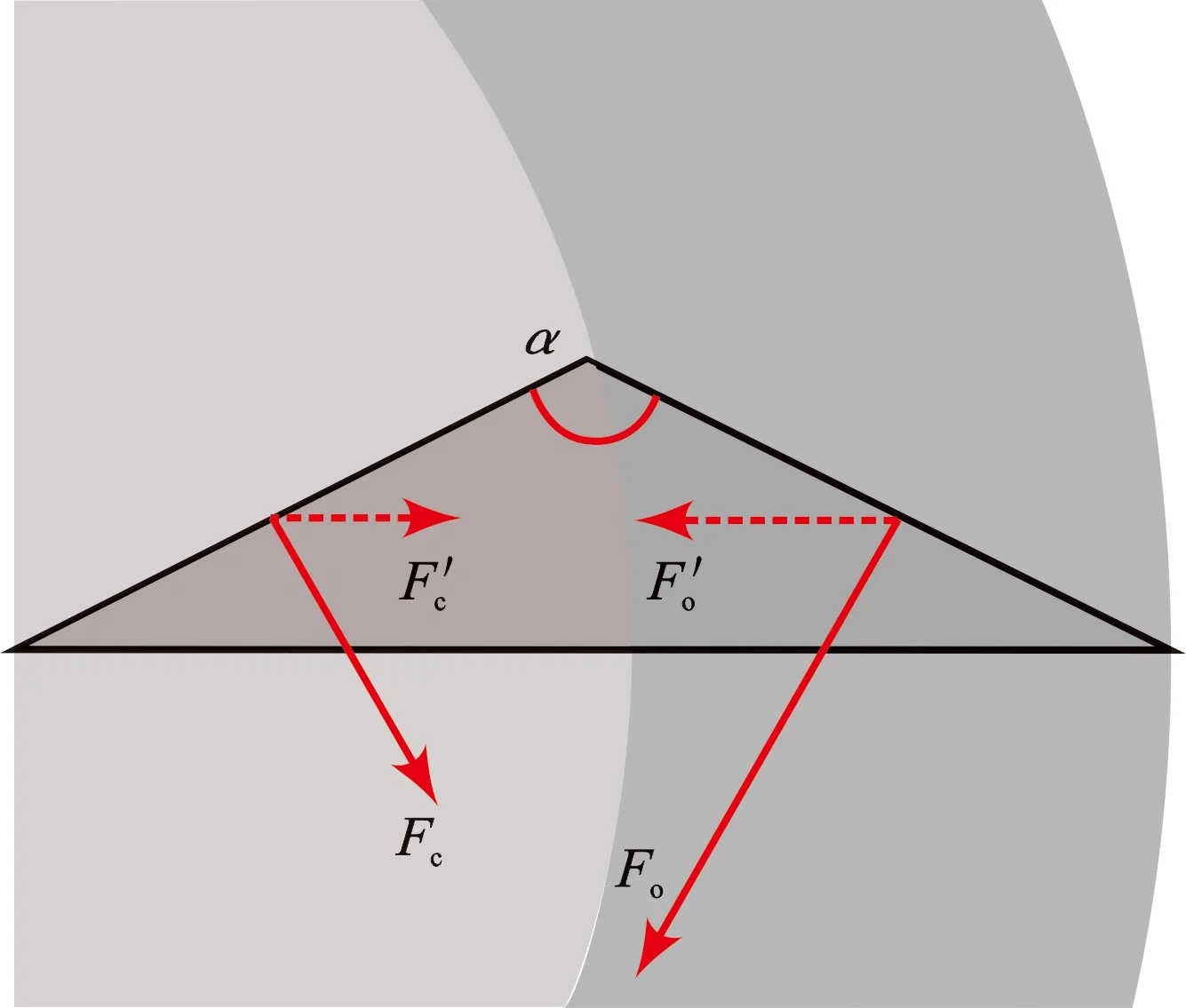
图14 多脊齿的切削岩石过程受力示意图Fig.14 Schematic diagram of stress in rock cutting process with multi-sridged cutters

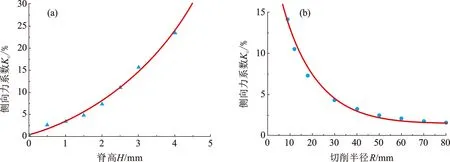
图15 多脊齿侧向力系数Fig.15 Lateral stress ratio of multi-ridged cutters

由图15(a)可知侧向力系数随着脊高的增高、脊角的变小而增高,呈指数形式,切削半径为28 mm时,脊高2 mm、脊角151°的4号齿侧向力系数大于5%。进而选取4号齿为模拟对象,改变切削半径,测试不同切削半径R的多脊齿侧向力系数,模拟结果如图15(b)所示,拟合公式为

Kc=-3.16ln(R-7.88)+14.58.

(9)

随着切削半径增大,多脊齿侧向力系数变小,在R=28 mm处小于5%。考虑到钻头心部布齿数量少,多脊齿的侧向力将影响其寿命和破岩效果,故钻头心部不适宜布多脊齿,选取脊高小于1.5 mm、脊角大于151°且切削半径大于28 mm为多脊齿破岩效果最佳区间。

4 结 论

(1)多脊齿的切削力及机械比能随着脊角的变小而减小,且脊角不存在最优区间,脊角变小也使多脊齿吃入地层能力增加,脊角在132°～158°多脊齿吃入性能相对稳定,脊角为126°的多脊齿吃入地层所需轴向力相较平面齿低41%。

(2)多脊齿在花岗岩中的最佳切削深度为2 mm,小角度地改变脊角对机械比能的影响很小,多脊齿轴向上消耗的机械比能是切向的1.2～1.5倍。

(3)特殊的几何形状会使多脊齿更易出现接触应力集中现象,并在旋转破岩时存在侧向力,通过对多脊齿内外两侧的受力情况进行分析,得到了单齿侧向力系数与切削半径间的关系,当脊角大于151°且多脊齿切削半径大于28 mm时破岩效果最佳。