基于三参数威布尔分布模型的超高强度抽油杆概率疲劳寿命曲线
2022-09-05蔡文斌胥元刚
蔡文斌,李 文,胥元刚
(1.西安石油大学石油工程学院,陕西西安 710065;2.中国石油新疆油田分公司,新疆克拉玛依 834000)
抽油杆分为C、K、D、KD、HL、HY等6级别,其中HL、HY级统称为超高强度抽油杆。超高强度抽油杆疲劳强度比D级抽油杆高一个等级,提高了其使用寿命,延长了油井免修期,在许多油田得到了广泛使用[1-4]。国内外多位学者对抽油杆概率疲劳寿命(P-S-N)曲线拟合进行了研究[5-8];樊松等[9]以幂函数形式的Basquin公式拟合得出了疲劳寿命预测模型;宋开利[10]用对数正态分布对抽油杆疲劳数据处理得到直线形式的抽油杆P-S-N曲线;房军等[11]研究了D级空心抽油杆的P-S-N曲线和疲劳极限图。以上抽油杆P-S-N曲线拟合都是采用假定疲劳寿命服从正态分布的Basquin模型。然而研究表明,受应力、试验样品差别等影响,疲劳寿命试验数据的分布并不完全满足正态分布,这就可能降低Basquin模型的疲劳寿命预测精度[12-13]。除了基于正态分布的Basquin模型,威布尔分布模型在P-S-N曲线疲劳寿命预测中也得到了广泛应用,多位学者进一步开展了基于正态分布的Basquin模型和威布尔分布模型在P-S-N曲线拟合方面的对比研究[14-15]。徐家进[16]研究了威布尔分布在疲劳统计学智能化方面疲劳寿命置信区间的问题,给出了在高镇同法基础上的一个智能化解决方法;韩庆华等[17]基于威布尔分布建立了铸钢及对接焊缝腐蚀疲劳寿命评估方法;Strzelecki[18]用三参数威布尔分布确定了不同应力水平下的低失效概率疲劳寿命;Paul等[19]基于威布尔分布进行了S355J2+N钢的P-S-N曲线拟合;陈建桥[20]通过比较正态分布和威布尔分布模型发现当加载应力高出50%疲劳极限应力时,寿命分布较好地遵从威布尔分布;闻德兵[21]通过对2024-T3Alclad 铝合金疲劳寿命概率分布类型对比研究发现,三参数的威布尔分布的灵活性和精度都要优于两参数的对数正态分布;邬华芝等[22]研究了结构疲劳破坏寿命特性概率统计方法中威布尔分布和正态分布的应用。笔者基于三参数威布尔分布建立超高强度抽油杆疲劳寿命预测模型,拟合HL和HY两种类型超高强度抽油杆的P-S-N曲线,采用柯式(K-S)检验法对疲劳试验数据进行威布尔分布及正态分布拟合优度检验,并与Basquin模型和威布尔模型疲劳寿命预测精度进行对比。
1 疲劳试验
1.1 试验样品制备
试验样品的尺寸严格按照石油与天然气行业标准制备,如图1所示。抽油杆试件长度为(500±50)mm,其制造工艺和批量生产工艺一致。
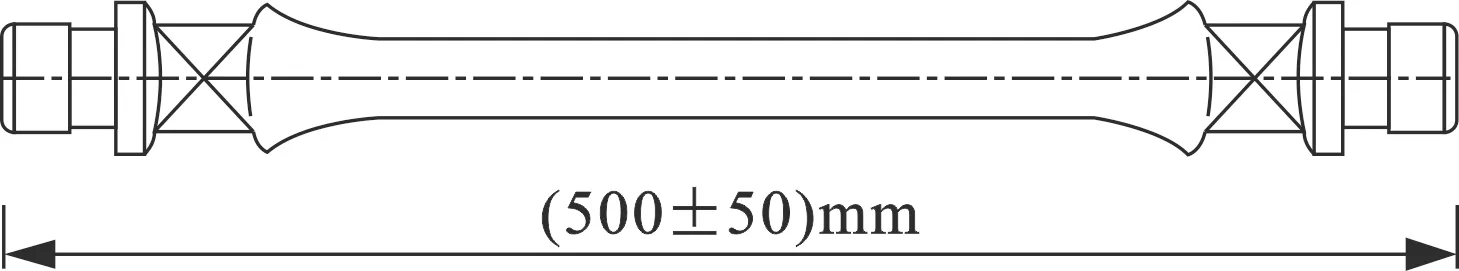
图1 疲劳试验抽油杆试件示意图Fig.1 Schematic diagram of sucker rod specimen for fatigue test
1.2 试验过程及结果
按照《SY/T 5029-2013抽油杆》钢制抽油杆疲劳性能测试要求,采用PLG-300C电磁谐振高频疲劳试验机(图2)分别进行超高强度抽油杆(HL型和HY型)疲劳寿命试验。每一类型抽油杆分3组应力水平进行试验,每组试验5根试件,加载频率小于150 Hz,应力比R为0.1的拉-拉载荷,记录各个试验样本在500、540以及600 MPa应力下发生疲劳破坏前所经受的应力循环次数,即疲劳寿命,试验结果如表1所示。试件断裂后的部分样品如图3所示。

图2 PLG-300C电磁谐振高频疲劳试验机Fig.2 PLG-300C electromagnetic resonance high frequency fatigue testing machine
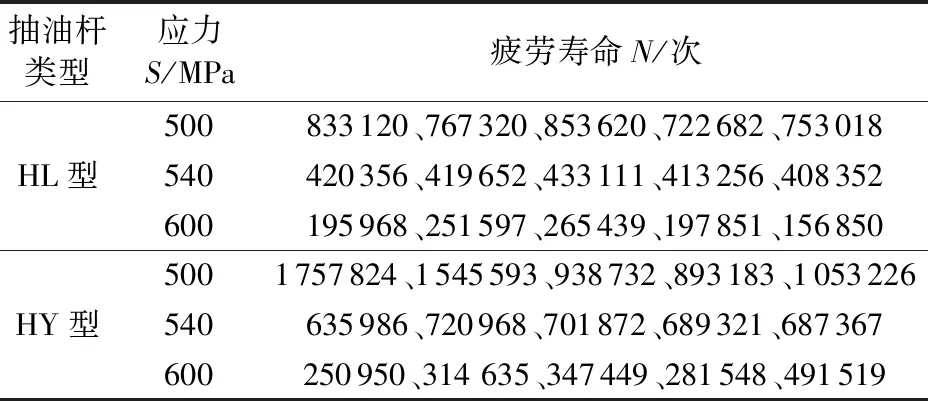
表1 HL型和HY型抽油杆疲劳试验结果Table 1 Fatigue test results of type HL and type HY sucker rods

图3 断裂后的部分试样Fig.3 Part of sample after fracture
2 基于三参数威布尔分布疲劳寿命模型建立
2.1 疲劳寿命模型
威布尔分布的累积失效分布函数[23-24]为
(1)
式中,x为疲劳寿命或疲劳寿命函数式;α∈R,为位置参数;β>0,为尺度参数;γ>0,为形状参数。
假定抽油杆疲劳寿命数据服从三参数威布尔分布,疲劳寿命函数为
x=(lgN-A)(lgS-B).
(2)
式中,B为应力修正参数;A为疲劳寿命修正参数。
基于三参数威布尔分布的抽油杆疲劳寿命模型方程为
(3)
其中(lgN-A)(lgS-B)≥α,根据式(1)对抽油杆疲劳试验结果进行拟合,主要是进行参数A、B、α、β、γ估值。
2.2 参数A和B的估值
用疲劳寿命N的平均值μ代替疲劳寿命x,则式(2)可变形为
(4)
构建函数为
(5)
式中,n为样本容量;μ为疲劳寿命N的平均值;Ni为应力Si对应的疲劳寿命。由疲劳数据根据式(4)和(5)运用线性回归方法拟合,当Q取最小值时得到A、B的值。
2.3 参数α、β、γ的估值
可以利用概率加权矩法估计三参数威布尔分布α、β、γ的值[17-18,25],三参数威布尔分布的概率加权矩函数可以写为
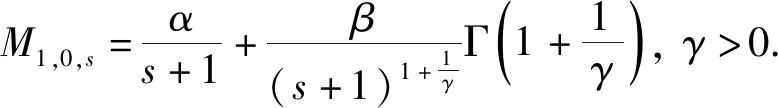
(6)
令s=0、1、2,代入式(6)中可得

(7)
由式(7)得威布尔分布的3个参数表达式分别为
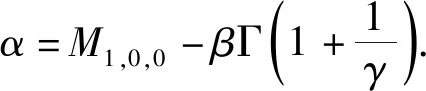
(8)
(9)
(10)
根据试验数据求出概率加权矩M1,0,s,再结合式(8)~(10)可以求出α、β和γ,M1,0,0、M1,0,1和M1,0,2的计算公式分别为:

(11)
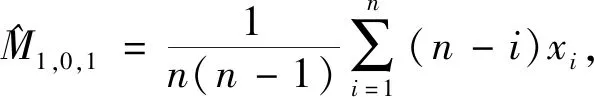
(12)
i)(n-i-1)xi.
(13)
式中,xi为抽油杆疲劳寿命数据,可以通过式(2)计算得到。
3 基于三参数威布尔分布P-S-N曲线拟合
通过计算得到HY和HL型抽油杆疲劳P-S-N曲线几何参数,如表2所示。

表2 抽油杆疲劳P-S-N曲线几何参数及威布尔分布参数Table 2 Estimated geometric parameters of HY and HL sucker rod fatigue P-S-N curves
根据式(3)得HY型和HL型抽油杆疲劳寿命模型分别为
P1(N|S)=1-exp
(14)
P2(N|S)=1-

(15)
根据三参数威布尔分布模型计算结果分别做出HY和HL型超高强度抽油杆对数坐标和普通坐标下的P-S-N曲线,如图4所示。
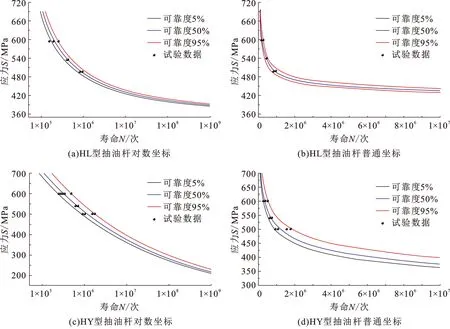
图4 三参数威布尔模型P-S-N曲线Fig.4 P-S-N curve of three-parameter Weibull model
4 基于正态分布的Basquin模型P-S-N曲线拟合
基于对数式Basquin模型S-N方程[4]为
lgS=lgC+mlgN.
(16)
式中,C和m为与试验材料加载方式相关的参数,可以通过线性回归的方法得到。
假设对数疲劳寿命lgN服从正态分布,为了拟合P-S-N曲线,则需要得到服从标准正态分布的疲劳寿命表达式,由正态分布理论得到指定概率下服从标准正态分布的疲劳寿命为
lgNp=μ+μpσ.
(17)
式中,lgNp为服从标准正态分布的对数疲劳寿命;μp为与概率P对应的标准正态偏量(查标准正态偏量获得);σ为对数疲劳寿命标准差。
采用最小二乘法对P-S-N曲线进行拟合,令B=lgC,A=m,构建拟合方程为
lgS=AlgNp+B,
(18)
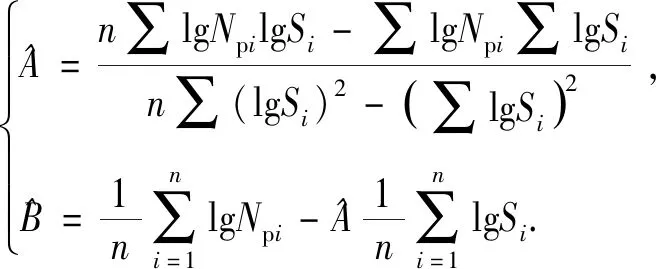
(19)
通过上面方法计算得到HY型抽油杆可靠度为99.99%和50%时,几何参数A、B分别为-0.096、3.265 3和-0.142 2、3.562 7;HL型抽油杆可靠度为99.99%和50%时,几何参数A、B分别为-0.066 3、3.105 6和-0.133 2、3.515 6。
根据式(19)可得到正态分布下两种概率下抽油杆的S-N曲线方程,对数坐标和普通坐标下的P-S-N曲线如图5所示。
5 两种模型对比
5.1 拟合优度检验
为了验证疲劳数据是否符合假定分布,需要进行拟合优度检验,常用的检验方法有χ2检验法、克拉美法以及柯式检验法(K-S)等[26]。
采用K-S检验法检验疲劳试验数据是否符合假定分布。试验数据服从假定分布记为H0,不服从假定分布记为H1,F0(x)为分布函数,Fn(x)为样本累积频率函数,即
(20)
式中,X(1)≤X(2)≤…≤X(n)为X(1),…,X(n)按照升序排列后的次序统计量。

图5 正态分布Basquin模型P-S-N曲线Fig.5 P-S-N curve of Basquin model with normal distribution
设D为F0(x)与Fn(x)差距的最大值,即D=max|Fn(x)-F0(x)|,当实际观测到D>D(n,α)时,拒绝H0假设;反之接受H0假设,其中D(n,α)可以通过K-S检验的临界值表查得。
以HY型抽油杆应力为500 MPa为例,5个试验数据,因此取显著水平α=0.05,查表可以得到临界值D(5,0.05)=0.563。利用K-S检验计算结果如表3所示。
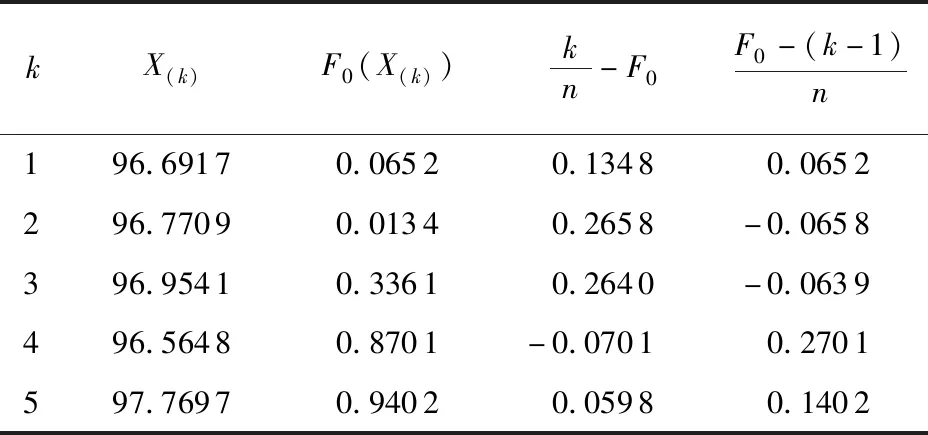
表3 K-S检验计算结果Table 3 K-S test calculation table
运用同样的方法,检验基于正态分布模型得到D的最大值为0.325,小于临界值,因此接受抽油杆疲劳寿命服从正态分布的假设,但是由于三参数威布尔分布的D更小,所以抽油杆疲劳寿命更加符合三参数威布尔分布。
5.2 拟合精度对比
对比图4、5,基于三参数威布尔分布的疲劳寿命模型拟合得到的曲线弯曲度更好,与试验数据更加贴合,基于正态分布的模型拟合得到的曲线和试验数据贴合度较低。随着应力及失效概率减小,基于三参数威布尔分布的疲劳寿命模型拟合得到的曲线逐渐变得平缓,趋近于疲劳极限,所计算概率下的曲线离散度较低更加符合实际情况,基于正态分布的模型拟合得到的曲线离散度更高,在低失效概率下疲劳寿命预测值更加保守,在高失效概率下的疲劳寿命预测值更加危险。
计算得到两种不同模型在可靠度为50%时的疲劳寿命,如表4所示。
由表4可以发现,基于正态分布Basquin模型计算得到的HL型、HY型抽油杆疲劳寿命与试验误差分别为12.50%和19.84%,基于三参数威布尔分布模型计算所得的疲劳寿命与试验误差平均值分别为1.25%和4.39%,拟合精度更高。
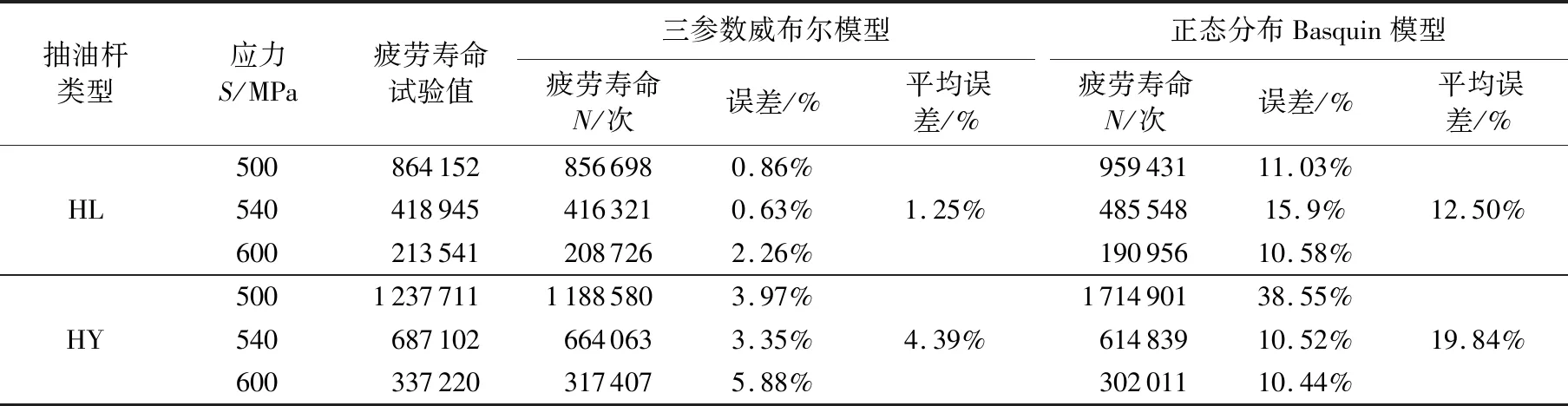
表4 两种模型的疲劳寿命Table 4 Fatigue life of two models
6 结 论
(1)抽油杆疲劳试验数据都符合威布尔分布和正态分布,相比正态分布,三参数威布尔分布拟合优度更高。
(2)疲劳寿命预测结果表明,基于三参数威布尔分布得到的HL型和HY型抽油杆疲劳寿命误差平均值分别为1.25%和4.39%,远低于基于正态分布Basquin模型的12.50%和19.84%,基于三参数威布尔分布的新模型拟合精度更高。
doi:10.7527/S1000-6893.2021.25138.
