一些二进制数列的族复杂度和互相关测度
2022-09-05梁嘉怡
梁嘉怡, 薛 盼
(西安欧亚学院 通识教育学院, 陕西 西安 710065)
随着计算机和互联网的普及, 传统的业务处理与服务等日常活动已经不能满足日益发展的新时代了. 目前人类已经进入了信息时代, 许多问题都可以通过计算机和网络等工具来实现. 此时, 伪随机二进制数列成为了密码系统中的一个常用工具, 并有着广泛的应用, 比如密码学、光谱学等[1-2].
为衡量二进制数列的伪随机性,引入了多种伪随机测度,比如f-复杂度[3],互相关测度[4],一致分布测度[5]等等. 本文将采用f-复杂度和互相关测度来衡量二进制数列的伪随机性.Mauduit和Sárközy[5]于1997年开始对伪随机二进制数列进行研究,构造出了一些“好”的数列,并分析讨论了其数列的伪随机性. Ahlswede等[3]给出了f-复杂度(f-complexity )的定义.
定义1长度为N的二进制数列EN∈{-1,+1}N的族F的f-复杂度C(F) 是指对于任意的1≤i1 ei1=ε1,ei2=ε2, …,eij=εj 成立的最大整数j≥0. 由定义1有2C(F)≤|F|,其中|F|表示族F的长度.Gyarmati等[4]给出了互相关测度(cross-correlation measure ) 的定义. 定义2长度为N的二进制数Ei,N=(ei,1,ei,2,…,ei,N)∈{-1,+1}N,i=1,2,…,F族F的l阶互相关测度Φl(F)为 其中:I=(i1,i2,…,il)∈{1,2,…,|F|}l,D=(d1,d2,…,dl)∈Zl满足0≤d1≤d2≤…≤dl 如果二进制数列族F具有“大”的f-复杂度和“小”的互相关测度,那么称其为“好”的二进制数列族. 然而构造具有这样性质的二进制数列,是信息安全领域中非常困难的问题.Gyarmati[6-7]给出了一些具有较“大”的f-复杂度的数列族,然而其互相关测度也很大,没有得到一个较好的结果.而文献[4]中的二进制数列族具有较小的互相关测度,但是其f-复杂度却很难衡量. Winterhof 等[8]证明了f-复杂度和互相关测度之间的关系. 其中log2表示二进制对数. 本文基于数论方法构造出更多具有“大”的f-复杂度和“小”的互相关测度的二进制数列族,用伪随机二进制数列来模拟真正的随机数列. 以下两个定理中给出了两个族均具有上述“好”的性质. 则有 且 则有 且 有关特征和估计的相关引理如下. 证明参见文献[10]中第三章. f(x)=c(x-x1)d1(x-x2)d2…(x-xs)ds 当i≠j时,xi≠xj,其中(d1,d2,…,ds)=1.设X,Y∈R满足0 证明参见文献[5]中定理2. 显然方程 1≤x≤M, 1≤i≤l 最多有2l个解. 则有 其中:M∈N,满足0≤d1≤… 其中 而 因此h(x)无平方因子.注意到h(x)是不可约的且无平方因子,而Legendre符号是二次特征,根据引理2有 从而 2l≤18lp1/2logp+2l≤20lp1/2logp 因此 Φl(F1)≪lp1/2logp,l=1,2,… 类似可证 (1) 需要证明 (2) 此外由引理1可得 由式(1)和式(2)以及命题1可得 那么 有关指数和估计的相关引理如下. 引理3[11]设g(x),h(x)∈Fp[x],f(x)=g(x)/h(x)在Fp上不为常值函数.设s表示g(x)的不同根的数目,则有 证明参见文献[11]中定理2. 引理4[12]设整数s1,…,sk,d1,…,dk满足(s1…sk,p)=1和d1<… 在Fp上不是零多项式. 证明参见文献[12]中引理7.1. 引理5设整数u,x,d1,…,dl,r1,…,rl,s1,…,sl满足d1 H1(x)=(x+d1)…(x+dl)y1…yl G1(x)=r1(x+d2)…(x+dl)y1…yl+…+ rl(x+d1)…(x+dl-1)y1…yl+ s1(x+d1)…(x+dl)y2…yl+…+ sl(x+d1)…(x+dl)y1…yl-1+ ux(x+d1)…(x+dl)y1…yl 显然函数G1(x)在Fp上不为常数,则由引理3可得 如果p|u,则有 定义 x+dl+1=y1,…,x+d2l=yl rl+1=s1,…,r2l=sl 可得 如果存在n,m使得n 若p|rn+rm,定义 对于F′1(x),若仍然存在n′,m′满足n′ 其中(t1…tk,p)=1,c1<… 因此 现在定义 有 综上可得,引理5证毕. 引理6[13]设χ是模q的非主特征,则对任意的整数M及正整数N有 证明参见文献[13]中第十三章. 证明定理2.首先考虑F2.设(i1,…,il)∈{1,2,…,|F2|}l,0≤d1≤…≤dl 有 (3) 同理 (4) 又有 (5) 由式(3~5)和引理5可得 因此 Φl(F2)≪lp1/2(logp)2l+1l=1,2,… (6) 需要证明 (7) 由引理6可得 那么 (8) 由式(6,7)和命题1可得 因此 致谢:本文得到西安欧亚学院校级科研基金(2022XJZK03,2020XJZK10)的资助,在此表示感谢.



1 主要结论



2 特征和的估计与定理1的证明






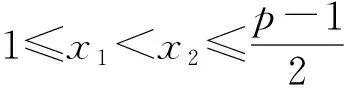

3 指数和的估计与定理2的证明











