受电弓系统可靠性评估的超椭球贝叶斯网络方法

2022-09-05齐金平周亚辉李少雄

兰州理工大学学报 2022年4期

齐金平, 周亚辉, 王康, 李少雄

(1. 兰州交通大学机电技术研究所, 甘肃兰州 730070; 2. 甘肃省物流及运输装备信息化工程技术研究中心, 甘肃兰州 730070; 3. 甘肃省物流与运输装备行业技术中心, 甘肃兰州 730070)

近年来，中国高铁发展速度快，运营总里程已占世界总里程的70% 以上，旅客发送量大幅增长，维修压力也随之日益凸显，动车组的运营可靠性备受关注.贝叶斯网络(Bayesian network，BN)的优势在处理复杂系统中的可靠性问题时广受青睐.随着研究的深入，贝叶斯网络得到了扩展，出现了离散、模糊、动态等贝叶斯网络[1-8].但是，现实工程数据缺失、信息多样化、模糊模型与概率模型对数据的强依赖性，在处理实际问题时限制了其作用的充分发挥.凸模型[9-11]对复杂系统不确定问题的处理能力显著，弥补了概率模型和模糊模型的不足，使其在可靠性分析中具有独特优势.区间贝叶斯网络从一定程度上使得信息缺失和不确定性对可靠性分析的影响降低，付果[12]以贝叶斯网络为起点，以风电功率概率为主线，为可靠性评估提供了更多信息；李硕[13]基于液压系统的时序性与动态性,提出证据理论结合离散贝叶斯网络的建模方法及向离散时间贝叶斯网络的转化；张瑞军等[14]以区间三角模糊子集为基础，构建了区间三角模糊多态贝叶斯网络模型，并对塔机倾覆事故进行分析.但实际中，各节点失效区间取极值的可能性几乎不会发生.超椭球模型[15-17]能使不确定性参数间的逻辑相关性得以表现，规避了区间极值情况.

本文以融入超椭球模型的新型贝叶斯网络对区间变量进行约束，同时通过求解受电弓系统不同故障状态下的灵敏度、后验概率等可靠性参数，确定了系统的高风险事件;经与模糊贝叶斯网络对比分析，证明了所提方法的实用性.

1 基本概念描述

1.1 证据理论

证据理论也是表达不确定知识的方法理论之一，可满足比概率更弱的条件系统，同时避免出现一部分不该出现的偏见.

定义1若Θ表示辨识框架，2Θ→[0,1]为基本概率分配函数m，假如A⊆Θ为任意子集，同时满足：

(1)

则m(A)为基本信任分配函数.

定义2若Θ为辨识框架，信任测度Bel:2Θ→[0,1]，似然测度Pl:2Θ→[0,1]，使∀A∈2Θ且A≠φ，有

且有对∀A∈2Θ:

Bel(A)≤Pl(A)

(5)

若{A为真}的可信度测度的真值为P(A)，则

Bel(A)≤P(A)≤Pl(A)

(6)

由式(6)可知，估计概率为一个区间，上下值分别为Bel(A)与Pl(A).

1.2 贝叶斯网络描述

1.3 新型贝叶斯网络描述

超椭球是根据距离反映偏离程度的方法，即随机向量在标准化空间下单位球坐标的原点和失效结构面的距离.

式(7)用超椭球模型表述为

(10)

引入矢量z，使xi的失效可能性完全落于超椭球域内，表述为

故而式(3)表述为新的超椭球模型：

(z-z0)T(z-z0) ≤1

(15)

(16)

根据式(15)，根节点失效在Δz=z-z0的超椭球空间内部随机取值，假如有(r,θ1,θ2,…,θn-1)，r∈[0,1]，θi∈[0,2π]为单位超椭球的坐标，则

(17)

进而，xi的失效可能性表述为

(18)

1.4 后验概率与灵敏度

(19)

(20)

其中:

(21)

根节点xi相对于叶节点T的灵敏度为

(22)

其中:ki为xi故障状态的数量.

2 动车组受电弓系统可靠性分析

受电弓系统是动车组的主要系统之一，根据受电弓系统构成与运行原理，结合现场实际故障类型以及参考文献[18]，构建BN如图1所示.各节点具体含义见表1.

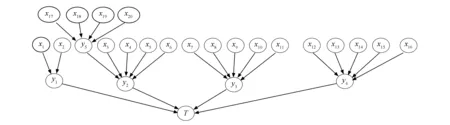
图1 受电弓系统BN

表1 节点含义

根据某铁路局历史故障数据，结合基于信心指数修正的专家调查法得到节点失效可能性区间，如表2所列.其中x1～x6为两种故障状态，x7～x20为三种故障状态.表3为中间节点y1的条件概率.

由表2、表3可得中间节点的失效可能性如表4所列.进而由式(8)得

P(T=[0,1])=(14.279, 17.136)×10-7
P(T=1)=(35.365, 48.093)×10-7

表2 节点失效可能性区间

表3 中间节点y1的条件概率

由式(19)得各节点后验概率如表5所列.由式(20～22)可得各节点灵敏度如表6所列.

由表5、表6可知，系统轻微故障时，x12、x16、x19、x10灵敏度大；系统完全故障时，x12、x19、x14、x15灵敏度大，对系统可靠性影响大，为高风险事件.虽然x13灵敏度大，但其故障概率是0，是小概率而非高风险事件.同时可见，超椭球BN所得结果区间更小，一定程度上解决了模糊贝叶斯网络分析保守的问题.