“定黏假设”对伴随系统求解和梯度精度影响

吴航空，王丁喜，黄秀全，徐慎忍

西北工业大学 动力与能源学院，西安 710072

随着计算机技术的发展，基于计算流体力学(CFD)的叶轮机设计优化方法获得了较快发展。目前，得到应用的优化设计方法大致可分为两类：全局优化方法和局部优化方法。全局优化方法虽然可以获得全局最优解，但是需要进行百次甚至千次CFD计算。在计算能力及计算资源有限的条件下，其应用受限。相较于全局优化方法，局部优化方法虽然只能获得局部最优解，但是其在计算耗时方面具有较大优势。此外，由具有一定经验研究人员设计的叶轮机叶片往往很接近最优结果，这种局部最优解甚至就是全局最优结果。

一般而言，局部优化方法需要获得目标函数关于设计变量的梯度信息，也称目标函数的灵敏度。有限差分方法和线化方法是最早得到应用的两种灵敏度计算方法。前者的灵敏度计算精度与扰动步长相关。扰动步长太大，截断误差会对计算结果精度产生较大影响；扰动步长太小，消去误差将是误差的主要来源。后者通过求解线化方程获得灵敏度信息，其灵敏度计算精度高且不受扰动步长的影响。然而，这两种方法的共同缺点在于其CFD计算次数与设计变量的维度线性相关。高负荷和高效率等的设计要求使得叶轮机叶片具有复杂的三维弯、扭、掠结构，参数化该叶片外形往往需要成百上千个设计变量，意味着成百上千次CFD计算。对于叶轮机内部多设计变量优化问题，有限差分及线化方法的计算耗时仍然不可接受。相比于上述两种方法，伴随方法是一种更加高效的梯度计算方法。每步寻优过程只需分别求解一次非线性流场和线性伴随场，而与设计变量的个数无关。对于多设计变量优化问题，这大大减少了优化所需要的计算耗时，适合日常工程应用。

伴随方法有两种形式：连续伴随方法和离散伴随方法,具体的操作流程如图1所示。连续伴随方法首先由微分形式的控制方程，经过数学推导获得微分形式的伴随方程，然后离散求解。而离散伴随方法是在离散控制方程的基础上获得离散形式的伴随方程。由于离散伴随方法的离散格式与离散的流动控制方程具有更好的一致性，灵敏度计算精度高，因此本研究主要基于离散伴随方法展开。

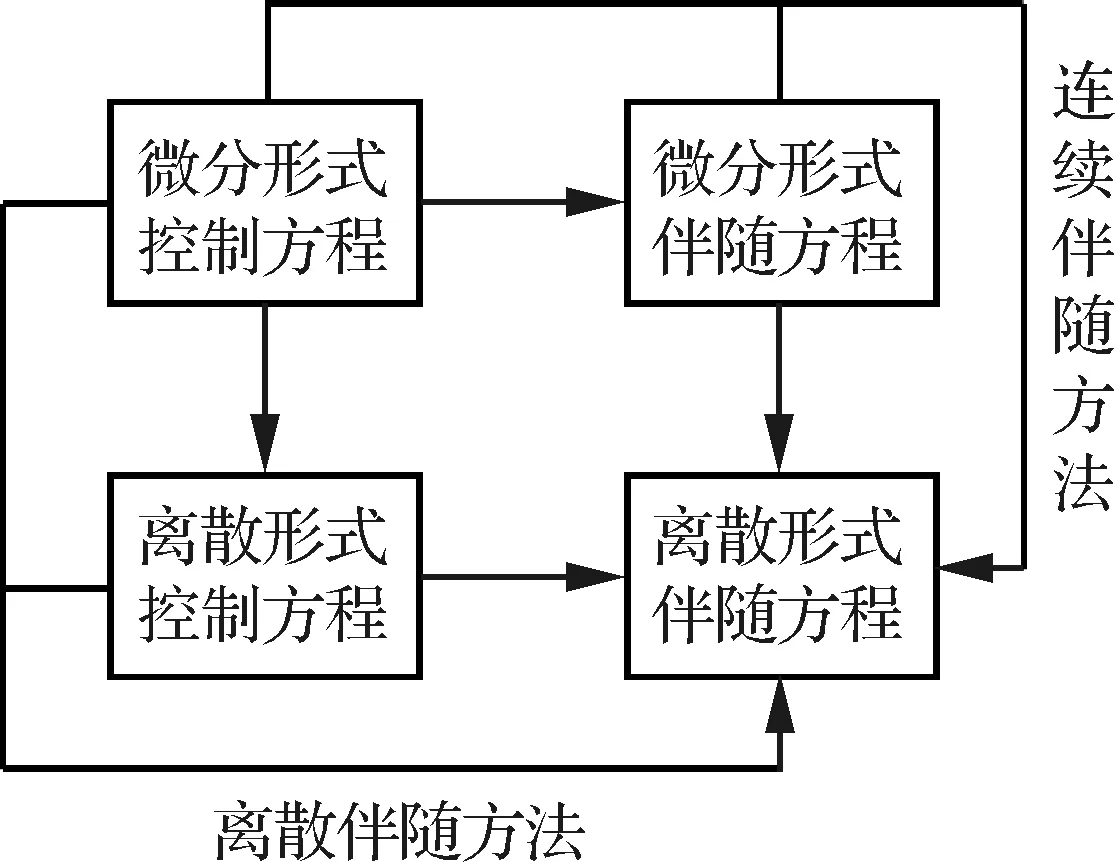
图1 连续伴随方法与离散伴随方法操作流程图Fig.1 Operation flow chart of continuous and discrete adjoint methods

离散伴随程序的开发可以通过手动微分实现，也可以借助自动微分软件。手动微分获得的离散伴随程序效率高，在计算时间和内存消耗方面具有一定优势，但是手动微分高精度格式和湍流模型方程等较为复杂和困难。此外，手动微分无法自动实现流场求解器和伴随求解器的同步调整。当对流场求解器的某一子程序进行修改时，需重新推导公式并微分这些子程序，过程繁琐，容易出错。自动微分可以完全实现伴随代码开发的自动化及流场代码与伴随代码的同步调整，程序的可维护性强。由于整个过程不需要手动微分代码，程序开发的工作量少，难度低。

随着自动微分技术的不断成熟，借助自动微分开发离散伴随求解器逐渐成为一种趋势。国外利用自动微分软件开发离散伴随求解器的应用较早。Giles等在2000年左右就开始应用自动微分软件TAPENADE微分流场求解器的子程序，然后再手动组装这些微分子程序。相比于对整个流场代码进行微分处理，此方法得到的离散伴随求解器效率高，计算耗时短。Albring等在开源软件SU2的基础上，借助自动微分软件开发出SU2的伴随功能，并以复步长变量法的结果作为参考，校验了该伴随求解器在梯度计算中的有效性和可靠性。国内，张朝磊等基于自动微分技术构建了离散伴随优化系统，并对二维无黏跨声速透平叶栅进行了气动优化设计。在保证质量流量不变的情况下，优化后出口熵增率减少8.82%，由此验证了该无黏离散伴随系统的正确性及有效性。

目前，在以中文形式公开发表的文献中还未发现基于自动微分技术的全三维湍流伴随的研究工作。无论是罗佳奇等的连续伴随方法还是马灿等的手动离散伴随方法，都未考虑黏性系数变化对灵敏度精度的影响，即采用“定黏假设”方法。“定黏假设”的引入可简化伴随方程的推导及子程序的微分过程，但是会引起灵敏度计算误差。在某些情况下，这些误差甚至会改变灵敏度的正负号，使得优化朝着完全错误的方向进行。另一方面，目前所研究的“定黏假设”方法同时忽略了层流及湍流黏性系数的影响，因而无法确定层流和湍流黏性系数对灵敏度精度影响程度。在实际应用过程中是否可以选择性冻结层流或者湍流黏性系数，在保证灵敏度精度的前提下，节省计算时间和存储。

针对上述问题，本文在自动微分软件TAPENADE逆向模式的框架下，介绍全三维湍流伴随求解器的开发过程包括子程序的微分及手动组装过程，特别是与黏性流动相关子程序的微分与组装。伴随灵敏度的验证采用线化求解器，而线化求解器的开发则是利用自动微分的正向模式。当伴随求解器与线化求解器都完全微分的时候，两种方法的雅可比矩阵互为转置，特征值相同，因此应该具有一致的灵敏度收敛性和相同的渐近收敛率。在此基础上，本文以跨声速NASA Rotor 67为研究对象，在两个不同工况点(近失速点及最高效率点)对比完全湍流伴随求解器与线化求解器的灵敏度精度、灵敏度收敛性和残差的渐近收敛率，并且分析研究不同“定黏假设”方法对伴随求解器计算结果的影响。

1 控制方程

三维圆柱坐标系下雷诺平均Navier-Stokes(RANS)方程为

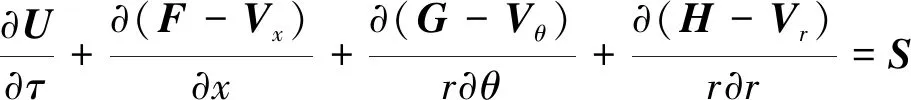
(1)

式中:

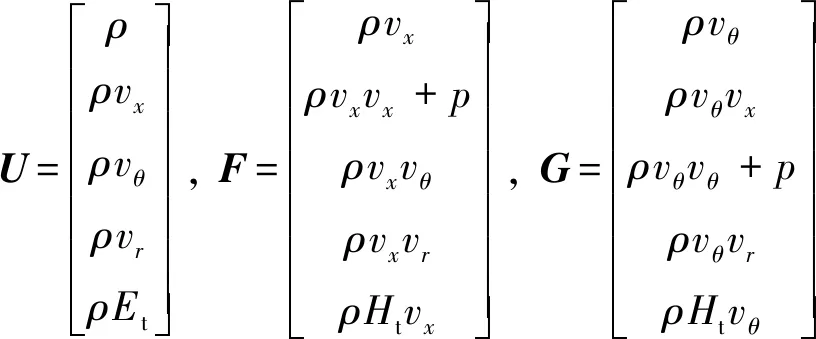
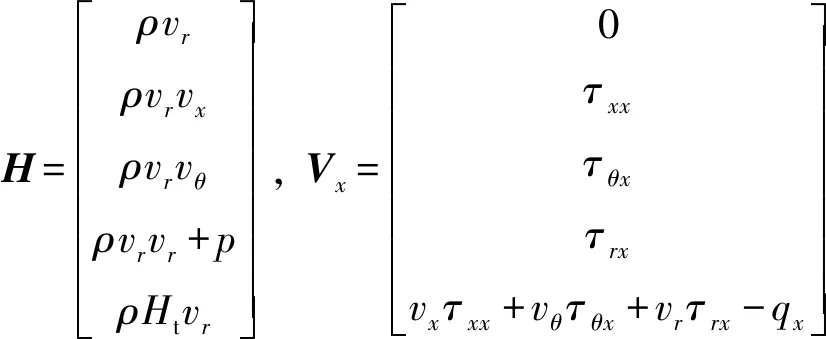
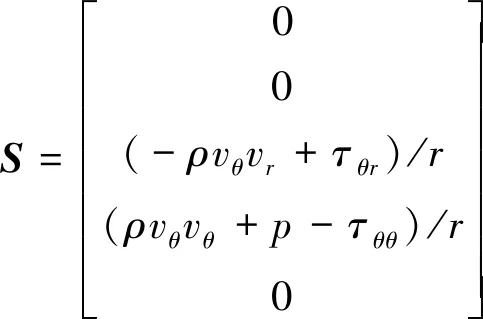
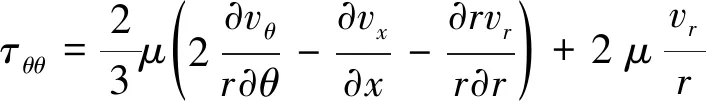
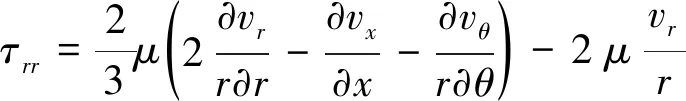
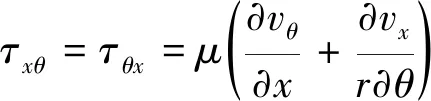
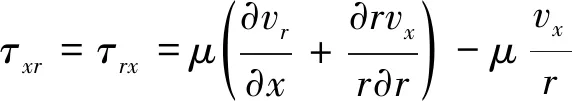
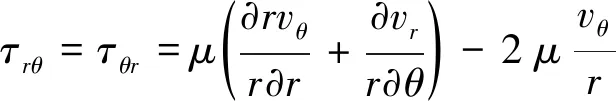
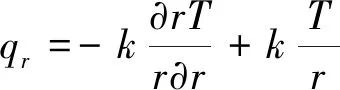
式中:为密度;为压强;为总内能；为总焓;、、分别为轴向、径向、周向速度;、、、、、为切应力;、、为正应力;为温度;为伪时间;、、分别为轴向、径向、周向热传导量；和分别为总的黏性系数和热传导系数,它们的值是其层流与湍流分量之和：

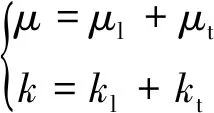
(2)

其中：下标l表示层流分量；t表示湍流分量。层流黏性系数由Sutherland定律确定：

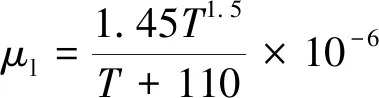
(3)

湍流黏性系数通过求解湍流模型方程获得，本文采用一方程Spalart-Allmaras(SA)湍流模型。SA模型的控制方程为

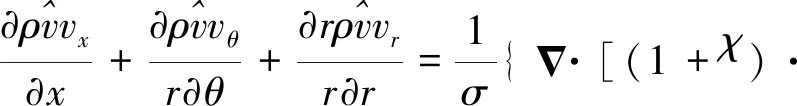
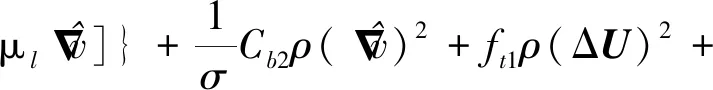
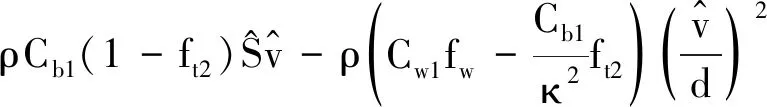
(4)

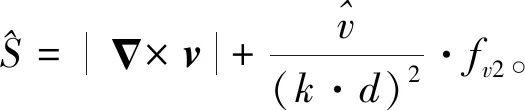
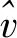
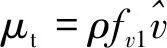
(5)

得到黏性系数后，可通过式(6)求解热传导系数：

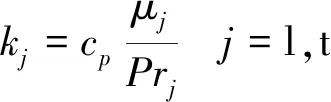
(6)

式中：为定压比热比；为普朗特数，其中为0.70，为0.90。

式(1)的时空离散格式为：对流项的离散采用中心差分加标量人工黏性；物理耗散项的离散采用高斯公式将体积分转化为面积分；伪时间项的离散采用显隐混合格式，即显式多阶龙格-库塔和隐式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)。

为了简化后续推导过程，式(1)可写成半离散格式：

(7)

式中：为对流项残差；为黏性项残差。

2 伴随方法

叶轮机内流优化问题的数学表达式为

min=(,,)

(8)

s.t.(,,)+(,,,,,)=

(9)

式(8)和式(9)分别为目标函数和约束。为设计变量;为计算域内部流场变量;为边界处的流场变量;为流场变量的空间一阶导数。由于计算域内部和边界处的流场变量在程序中的处理不同，因此将其分解为和。计算域内部和边界处的流场变量之间满足如下显式关系：

=(,)

(10)

黏性系数与设计变量及流场变量满足如下关系：

=(,,)=l,t

(11)

流场变量的空间一阶导数与设计变量及流场变量之间满足如下关系：

=(,,)

(12)

线化式(8)可得目标函数关于设计变量的灵敏度：

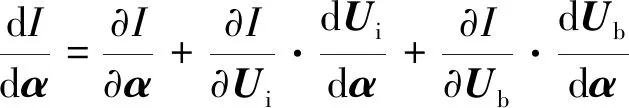
(13)

式中:和关于的灵敏度可通过求解方程式(9)的线化形式获得：

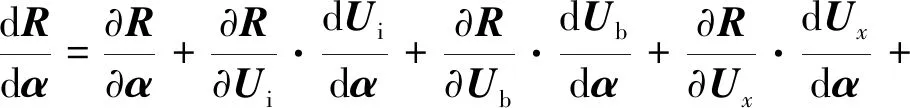
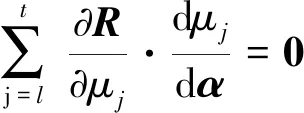
(14)

其中:

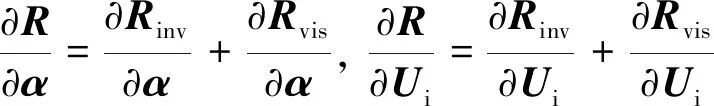
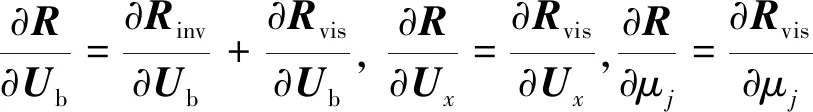
线化式(10)可得：

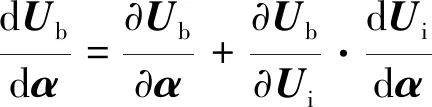
(15)

线化式(11)可得：

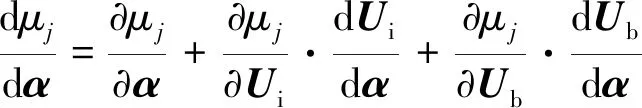
(16)

线化式(12)可得：

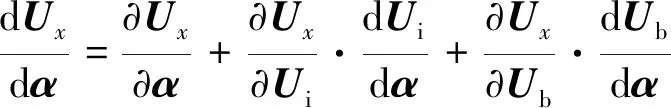
(17)

联立方程式(14)～式(17)可得：

(18)

式中:

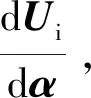
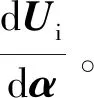
由方程(18)可得：

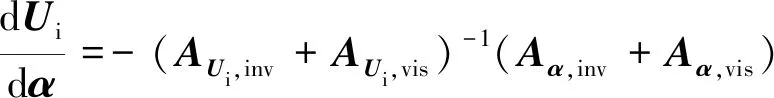
(19)

将式(15)和式(19)分别代入灵敏度计算式(13) 可得：

(,inv+,vis)(,inv+,vis)

(20)

(21)

线化方程(18)和伴随方程(21)的共同点在于都为线性方程，并且由于两种方法的雅可比矩阵互为转置，特征值相同，因此在线化求解器与伴随求解器都完全微分的前提下，两者应具有一致的灵敏度收敛曲线及相同的残差渐近收敛率。不同的是，线化方程(18)的右边项与设计变量相关，设计变量的个数决定了所需求解的线化方程的个数。伴随方程(21)的右边项与目标函数相关而与设计变量无关，所需求解的伴随方程个数与目标函数个数线性相关。对于叶轮机内流优化问题，设计变量的维度远远大于目标函数的维度，因而伴随方法更加高效。

在伴随方法发展的早期，为了简化推导过程，研究人员通常采用“定黏假设”方法，即不考虑黏性系数(包括层流和湍流)变化对伴随方程的影响，相应的雅可比矩阵的黏性部分,vis可简化为

(22)

,vis简化为

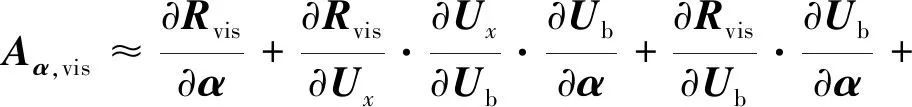
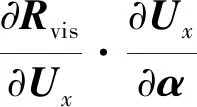
(23)

接下来将分别给出冻结层流黏性系数及湍流黏性系数时的雅可比矩阵。

1) 冻结湍流黏性系数，,vis和,vis为

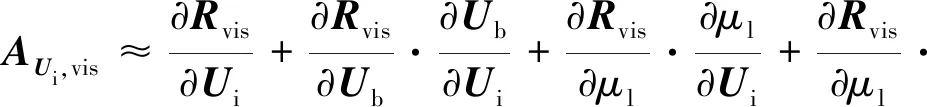
(24)

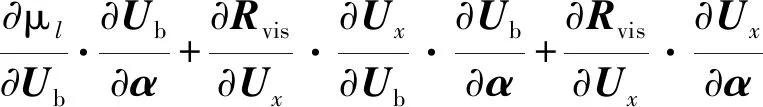
(25)

2) 冻结层流黏性系数，,vis和,vis为

(26)

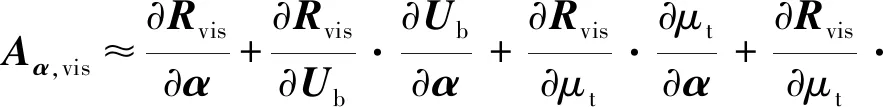
(27)

得到伴随方程的雅可比矩阵后，可通过时间推进方法迭代求解方程(21)获得伴随变量，然后将伴随变量代入式(20)得到目标函数灵敏度：

(28)

3 流场求解器及伴随求解器

本节将分别介绍流场求解器和伴随求解器的数据结构及子程序功能。

3.1 流场求解器

图2展示了流场求解器的流程图。要实现其功能，需要6个步骤，每步的具体功能如下：

INIT: 初始化流场。

图2 非线性流场求解器流程图Fig.2 Flow chart of nonlinear flow solver

Rinv: 计算对流项残差。

Viscous residual: 计算黏性项残差。黏性残差的计算包含4部分，如图3所示。

1) Ux: 计算流场变量的空间一阶导数。

2) SL: 应用Sutherland定律计算层流黏性系数。

3) SA: 求解湍流模型方程得到湍流黏性系数。

4) Rvis: 计算黏性项残差。

UPDATE: 求解控制方程(7)，更新内部流场变量。

BC: 施加边界条件，更新边界处的流场变量。

图3 黏性残差计算Fig.3 Calculation of viscous residual

OBJ: 计算目标函数。

上述6个步骤循环往复直到结果满足收敛要求。

3.2 湍流伴随求解器

本研究采用自动微分软件TAPENADE的逆向模式开发湍流伴随求解器，具体开发过程为：首先利用自动微分技术对流场求解器的主要子程序进行微分，然后对相应微分子程序按照一定的顺序手动组装。由于逆向模式的原因，手动组装伴随求解器的过程较为复杂。图4展示了湍流伴随求解器的流程图，下标a表示由自动微分逆向模式得到的变量或者子程序。从图中可以看出，湍流伴随求解器包含两部分：伴随方程的求解及灵敏度计算。伴随方程由于与设计变量的微分无关，因此在这一部分只微分流场变量，冻结设计变量。而灵敏度计算部分，需要微分设计变量。

图4 湍流伴随求解器流程图Fig.4 Flow chart of adjoint solver

3.2.1 伴随方程求解

伴随方程的求解需要7个步骤，每步实现的具体功能如下：

OBJ_A1: 计算目标函数关于和的伴随方向导数，并将其存储在和，可得：

(29)

式中:为输入变量，为目标函数的加权因子，只有一个目标函数时，通常将其设为1。

BC_A1: 将转化到中并累加(方框中+=为累加符号)到，可得：

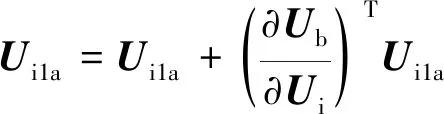
(30)

对比发现，方程(30)的-与伴随方程(21)的右边项一致。

INIT_A: 初始化伴随变量。为了保证线化求解器与湍流伴随求解器具有一致的灵敏度收敛曲线，需要将伴随变量初始化为0。

Rinv_A: 计算伴随方程对流项残差。

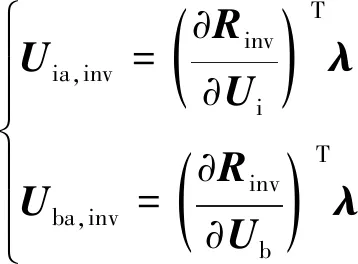
(31)

Adjoint Viscous Residual: 计算伴随方程的黏性项残差。黏性残差的计算包含4部分，如图5所示。

图5 伴随黏性残差计算Fig.5 Calculation of adjoint viscous residual

对比图4和图5发现，流场求解器的黏性项残差计算顺序与伴随求解器相反，这是自动微分逆向模式所导致的，因此在组装与黏性项残差计算相关微分子程序的时候，需要特别注意。

1) Rvis_A: 计算黏性项残差，并将其分别存储在、、、和。

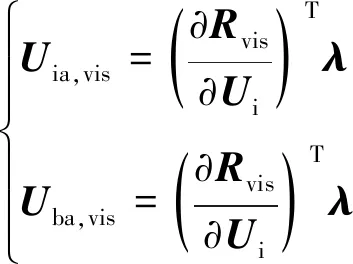
(32)

(33)

2) Ux_A: 将存储在a的黏性项残差转化到和，并累加。

(34)

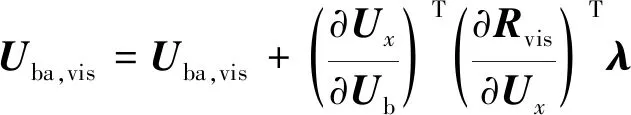
(35)

3) SL_A: 将存储在的黏性项残差转化到和，并累加。

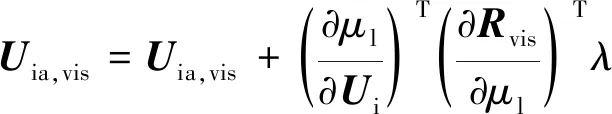
(36)

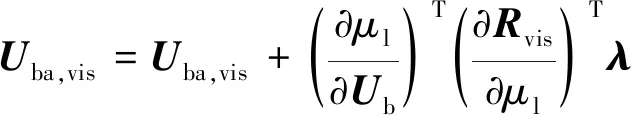
(37)

4) SA_A: 将存储在的黏性项残差转化到和，并累加。

(38)

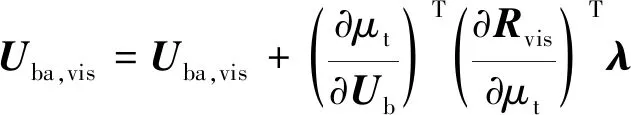
(39)

相加黏性项残差和对流项残差得到总残差：

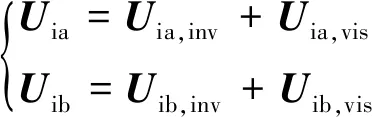
(40)

BC_A: 将存储在边界处的残差转化到流场内部并累加。

(41)

对比发现，方程(41)中的与伴随方程(21) 的左边项一致。

UPDATE_A: 更新伴随变量。

3.2.2 灵敏度计算

得到更新的伴随变量后，将其代入式(27)就可得到目标函数的灵敏度。具体数据结构如图6 所示。

图6 灵敏度计算Fig.6 Sensitivity evaluation

OBJ_A2: 计算目标函数关于和的伴随方向导数，可得：

(42)

注意：该微分子程序只需要被计算一次。将其放在灵敏度计算部分是为了方便读者理解，在实际程序开发过程中，该微分子程序通常被放在INIT_A(见图4)微分子程序之前。

Rinv_A2: 计算对流项残差关于和的伴随方向导数，可得：

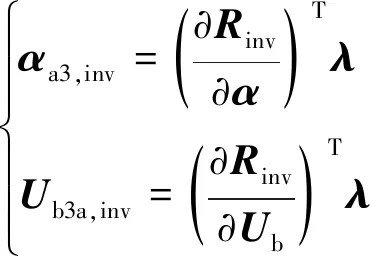
(43)

Adjoint Viscous Residual 2: 计算黏性残差关于和的伴随方向导数，此过程包含4步，如图7所示。

图7 完全湍流伴随方法黏性残差计算Fig.7 Calculation of adjoint viscous residual for ADJ

1) Rvis_A2: 计算黏性残差关于、、、和的伴随方向导数。

2) Ux_A2: 计算关于和的伴随方向导数，并累加。

3) SL_A2: 计算关于和的伴随方向导数，并累加。

4) SA_A2: 计算关于和的伴随方向导数，并累加。

上述4个步骤得到的和为

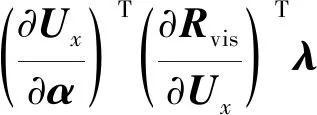
(44)

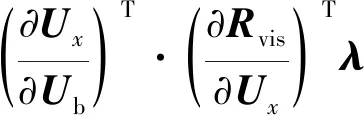
(45)

相加对应项可得：

(46)

计算灵敏度。

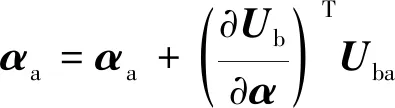
(47)

式中:的转置为所需求解的目标函数的灵敏度。

3.3 定黏假设

本节将介绍3种不同的“定黏假设”方法：① 冻 结层流及湍流黏性系数(FLEV)；② 冻结层流黏性系数(FLV)；③ 冻结湍流黏性系数(FEV)。为了节省空间，本节只对“定黏假设”伴随求解器与完全湍流伴随求解器存在差异的地方展开叙述。

3.3.1 冻结层流和湍流黏性系数

同时冻结层流和湍流黏性系数时，黏性残差的计算(见图5)将简化为图8。同理，灵敏度部分关于黏性残差的计算也做相应调整。为了节省空间，不再赘述。

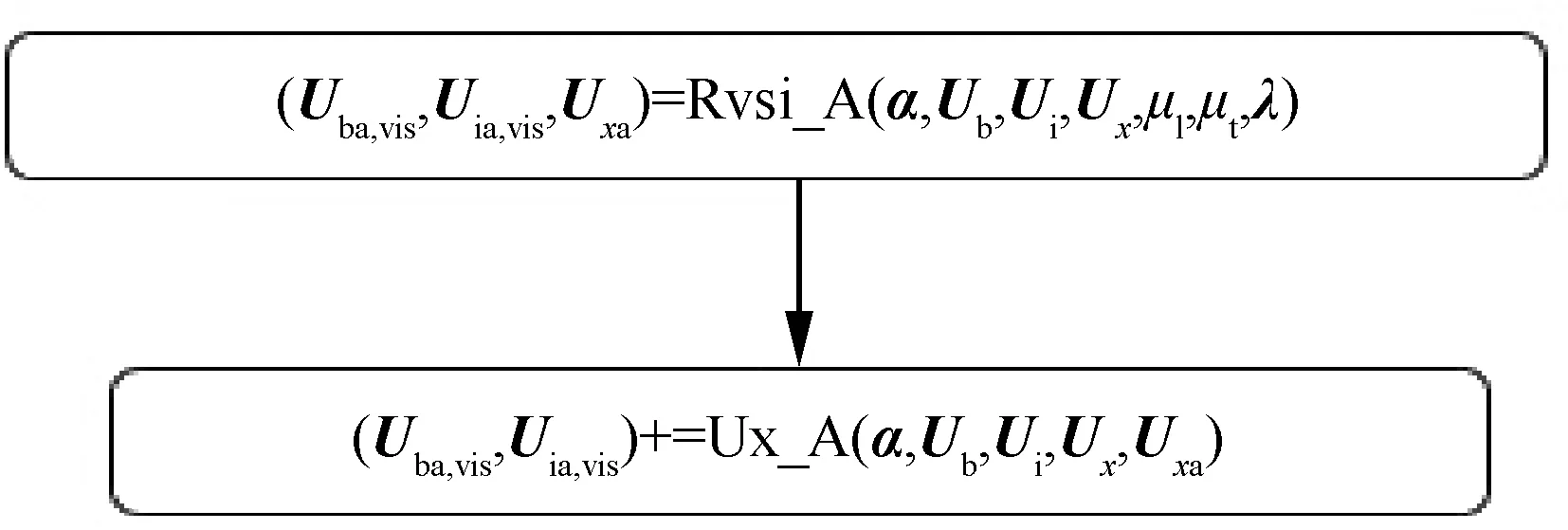
图8 冻结层流及湍流黏性系数时黏性残差计算Fig.8 Calculation of adjoint viscous residual with FLEV

3.3.2 冻结层流黏性系数

冻结层流黏性系数时，与黏性残差计算相关的微分子程序将简化为图9。灵敏度计算部分做同步调整。

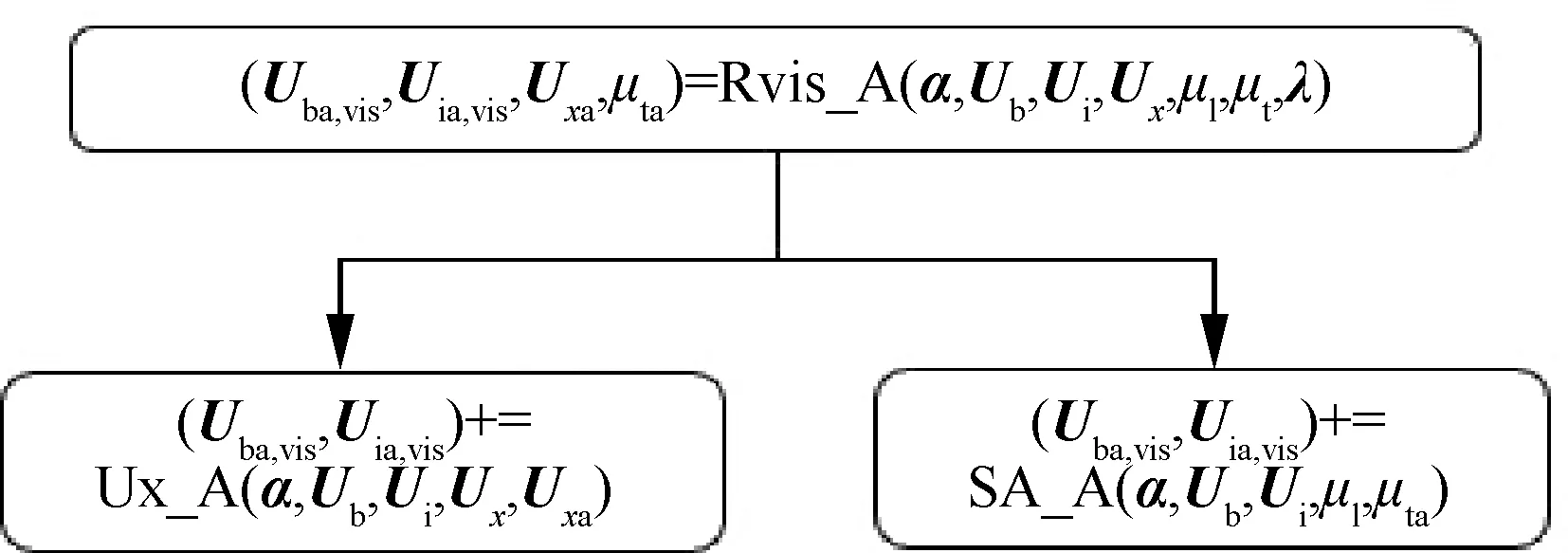
图9 冻结层流黏性系数时黏性残差计算Fig.9 Calculation of adjoint viscous residual with FLV

3.3.3 冻结湍流黏性系数

冻结湍流黏性系数时，与黏性残差计算相关的子程序将简化为图10,同步调整灵敏度计算部分。

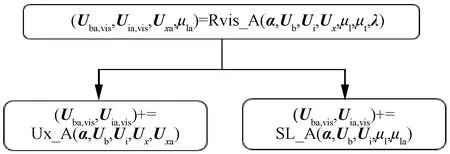
图10 冻结湍流黏性系数时黏性残差计算Fig.10 Calculation of adjoint viscous residual with FEV

4 流场求解器验证

本文以跨声速NASA Rotor 67为研究对象。NASA Rotor 67是NASA Lewis研究中心设计的双级压气机的第一级转子，其设计参数如表1 所示。

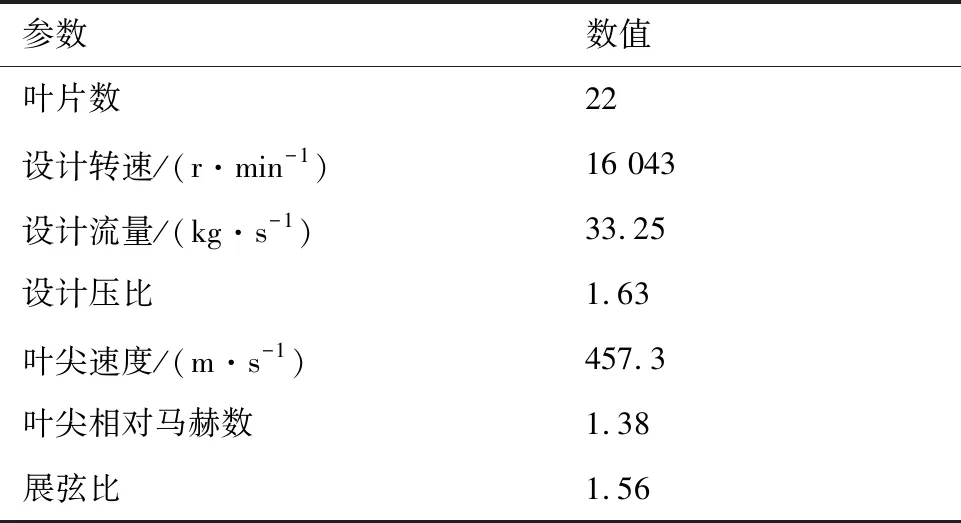
表1 跨声速NASA Rotor 67的设计参数Table 1 Design parameters of transonic NASA Rotor 67

首先做网格无关性验证，采用3套不同网格，分别为Grid1，Grid2和Grid3。Grid2的网格如图11所示，其周向和径向的网格点数都为65，轴向的网格点数为145(叶片表面的网格点数为81)，总的网格点数大约为613 000。相比于Grid2，Grid1和Grid3的网格点总数分别减小和增加一倍。

进出口为亚声速边界条件,在进口给定总温、总压及两个方向的气流角。总温及总压的大小分别为101 325 Pa和288.15 K，气流角为0°。在出口通过径向平衡关系获得背压沿径向的分布。为了避免解析黏性剪切底层，在壁面处采用滑移边界条件及壁面函数。对于叶片前缘之前和尾缘之后的周期性几何上采用周期性边界条件。

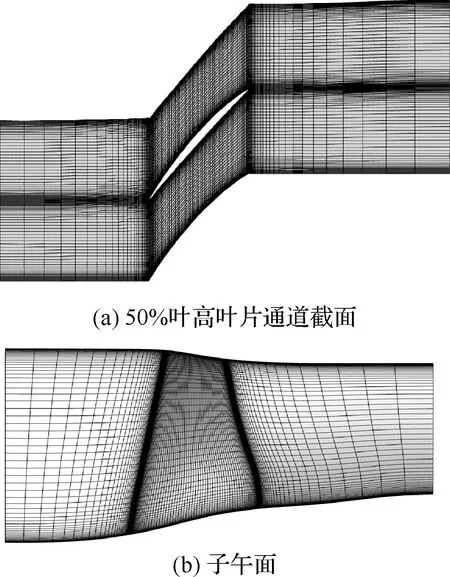
图11 NASA Rotor 67算例的计算网格Fig.11 Computational grid of NASA Rotor 67

通过改变出口背压，进行一系列计算，得到NASA Rotor 67在100%转速下的特性线。图12(a) 为流量-压比特性图，图12(b)为流量-效率特性图。两幅图的横坐标通过实验测得的堵塞流量(34.96 kg/s)无量纲化得到。从图12可以看出，Grid1的结果与Grid2和Grid3的结果存在差异，但Grid2和Grid3的计算结果基本重合。为了节省计算时间和计算存储，接下来的灵敏度验证部分采用Grid2。

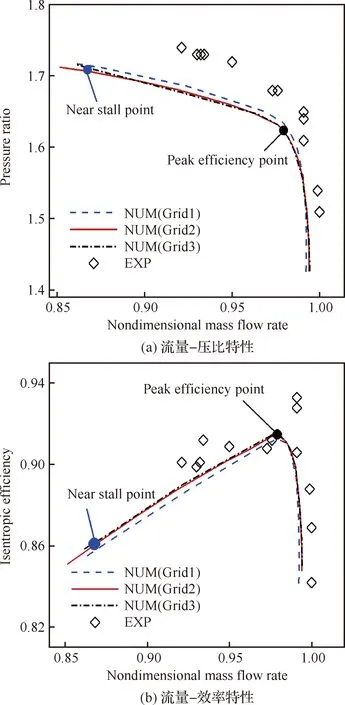
图12 100%转速下NASA Rotor 67算例的特性线Fig.12 Performance characteristics of NASA Rotor 67 at 100% design speed

5 结 果

本文选取数值结果的最高效率点及近失速点两个不同工况(如图12所示)验证全三维湍流伴随求解器的稳定性、灵敏度精度、灵敏度收敛性及残差的渐近收敛率，并与“定黏假设”结果和线化求解器结果进行对比。最高效率点与近失速点的性能参数如表2所示。

伴随求解器的验证部分只考虑性能参数关于边界条件(入口总温)的灵敏度。这样做的好处在于灵敏度计算部分不需要对与几何变量相关的参数进行微分，简单、易于操作，并且由于验证过程不涉及网格扰动，因而可以避免由于网格扰动所造成的误差。性能参数包括出口质量流量和面积平均总压。其中，前者为RANS方程守恒变量的线性函数，而后者为RANS方程守恒变量的非线性函数。

表2 NASA Rotor 67最高效率点与近失速点性能参数

5.1 最高效率点

图13给出了最高效率点98%叶高处的相对马赫数云图。从图中可以看到，通道内有较强激波，并且激波前的马赫数为1.4，激波的存在使得流场具有较强的非线性。这种复杂非线性流场给湍流伴随求解器的验证工作带来挑战，但同时也能更进一步验证湍流伴随求解器的有效性及鲁棒性。

图13 最高效率点98%叶高的相对马赫数云图Fig.13 Relative Mach number contours at 98% span at a peak efficiency point

5.1.1 流场及伴随场

图14(a)为50%叶高处的湍流变量云图，图14(b) 为与湍流方程所对应的伴随变量云图。对比两幅图发现，流场变量的下游为伴随变量的上游，反之亦然。这一特征在一定程度上能用来对湍流伴随求解器进行定性的校核。

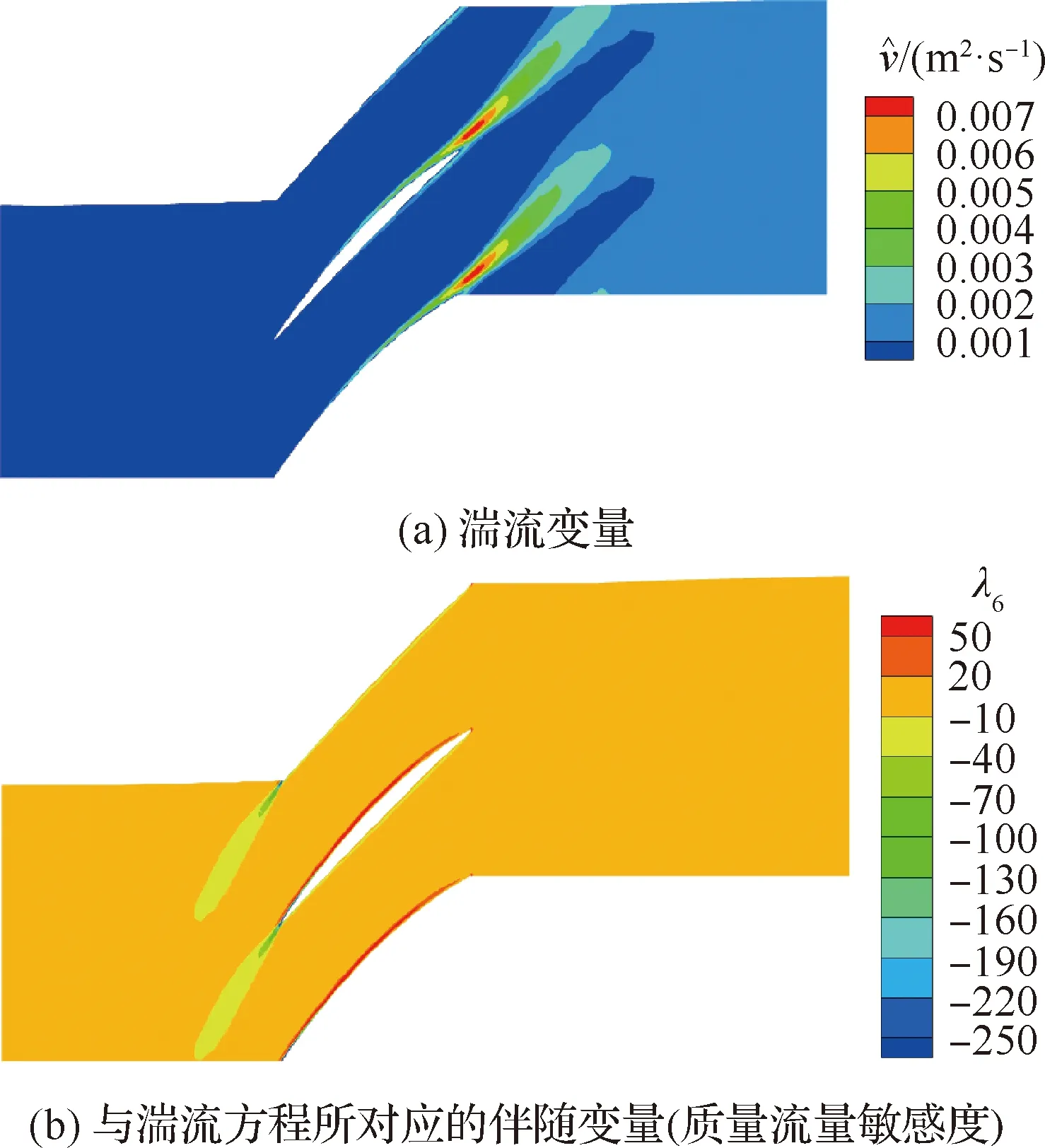
图14 50%叶高处湍流变量及与湍流方程对应的伴随变量Fig.14 Flow turbulence variables and adjoint variables corresponding to turbulence model equation at 50% span

5.1.2 灵敏度收敛性及精度

图15分别展示了质量流量d/d与总压灵敏度d/d收敛曲线。图中，ADJ表示完全湍流伴随求解器，ADJ(FLV)表示冻结层流黏性系数的伴随求解器，ADJ(FEV)表示冻结湍流黏性系数的伴随求解器，ADJ(FLEV)表示同时冻结层流和湍流黏性系数的伴随求解器，LIN表示线化求解器。

以线化求解器结果作为参考，ADJ的灵敏度相对误差不超过千分之一(如表3所示)。而“定黏假设”方法对伴随灵敏度精度及收敛性有较大影响。相比于FLV，FEV对伴随灵敏度的精度影响更大。前者影响不超过1%，而后者的影响超过了5%。对于质量流量灵敏度，FLV会使得伴随灵敏度增大(相比于LIN)，而FEV会使得伴

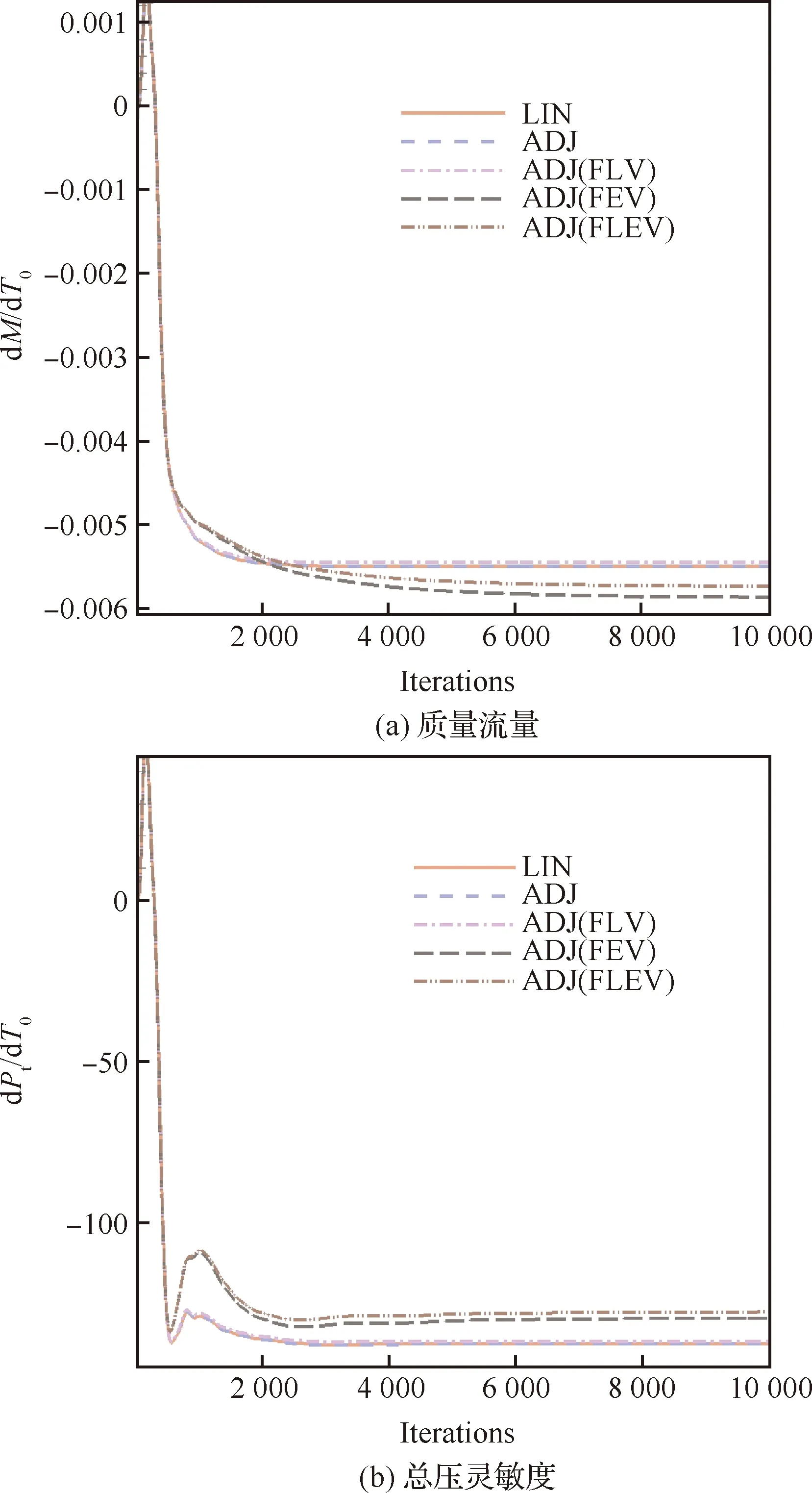
图15 最高效率点伴随求解器灵敏度与线化求解器灵敏度收敛曲线Fig.15 Sensitivity convergence histories of adjoint and linear solvers near a peak efficiency point

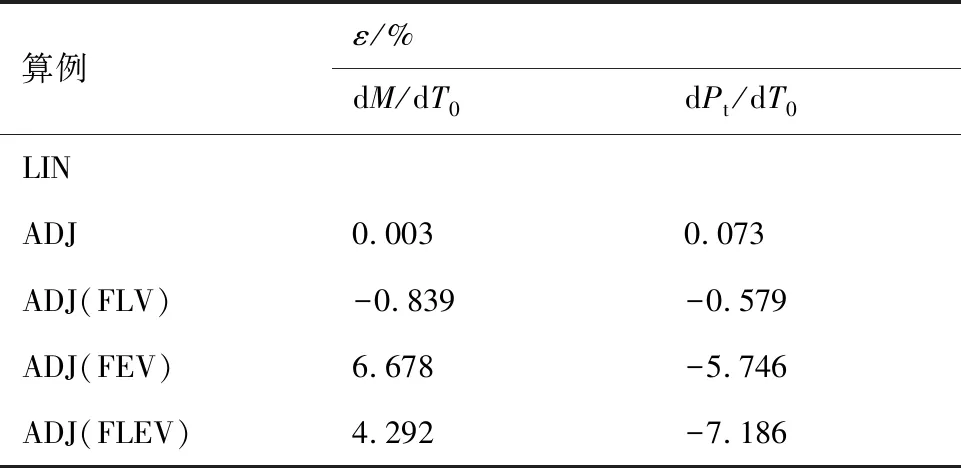
表3 最高效率点伴随灵敏度相对误差

随灵敏度减小，并且影响程度远远大于FLV。当采用FLEV的时候，FLV和FEV的影响会相互抵消一部分，因而ADJ(FLEV)的相对误差反而小于ADJ(FEV)，但是仍然大于ADJ(FLV)。此外，相比于质量流量灵敏度，FLEV对总压灵敏度的影响更大。采用FLEV，质量流量灵敏度的相对误差为4.30%，而总压灵敏度的相对误差为7.19%。综上可得，FLEV对非线性目标函数的影响要大于线性目标函数。

5.1.3 残差的渐近收敛率

在展示残差收敛曲线之前，首先介绍一下渐近收敛率的定义。式(7)的迭代格式可写为

+1=-Δτ()

(48)

式中:为总的残差，包括对流项残差与黏性项残差;为迭代步数。假设为控制方程(48)的精确解，则数值结果与精确解的误差为：

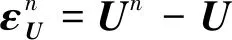
(49)

将方程(49)代入方程(48)，并做一阶泰勒展开可得：

(50)

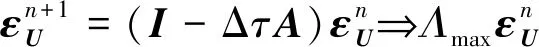
(51)

即矩阵-Δτ的最大特征值决定着误差的渐近收敛率。

线化方程(18)的误差渐近收敛率的表达式与非线性方程(51)的完全一致。为了节省空间不再赘述。接下来只针对伴随方程(21)推导其误差的渐近收敛率表达式。离散伴随方程(21)可得：

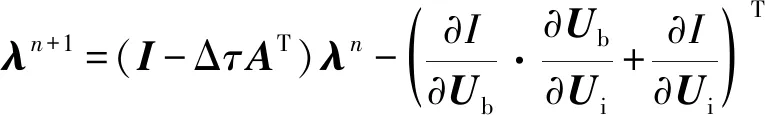
(52)

假设为控制方程(52)的精确解，则数值结果与精确解之间的误差为

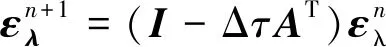
(53)

因为与互为转置，特征值相同，因此矩阵-Δ与矩阵-Δτ的特征值相同，最大特征值也相同。由渐近收敛率定义可知，方程(53) 的渐近收敛率与方程(51)相同。从数值结果的角度分析就是完全湍流伴随残差与线化残差的收敛曲线的斜率相同。当采用“定黏假设”方法的时候，由于其影响伴随方程的雅可比矩阵的特征值，从而影响渐近收敛率，使得伴随残差与线化残差的收敛曲线不一致。

图16展示了线化残差与伴随残差的质量流量和总压灵敏残差收敛曲线(RMS为所有变量的均方根误差，并取对数)。图16(b)中的黑色虚线为ADJ残差收敛曲线的平均斜率曲线。从图中可以看出，ADJ与LIN的残差收敛曲线的斜率相同，即一致的渐近收敛率。FLV对渐近收敛率影响较小，ADJ(FLV)的残差收敛曲线与ADJ重合。而FEV和FLEV对渐近收敛率影响较大。无论是质量流量还是总压灵敏度，FEV和FLEV都使得残差收敛曲线斜率的绝对值变小，收敛变慢。

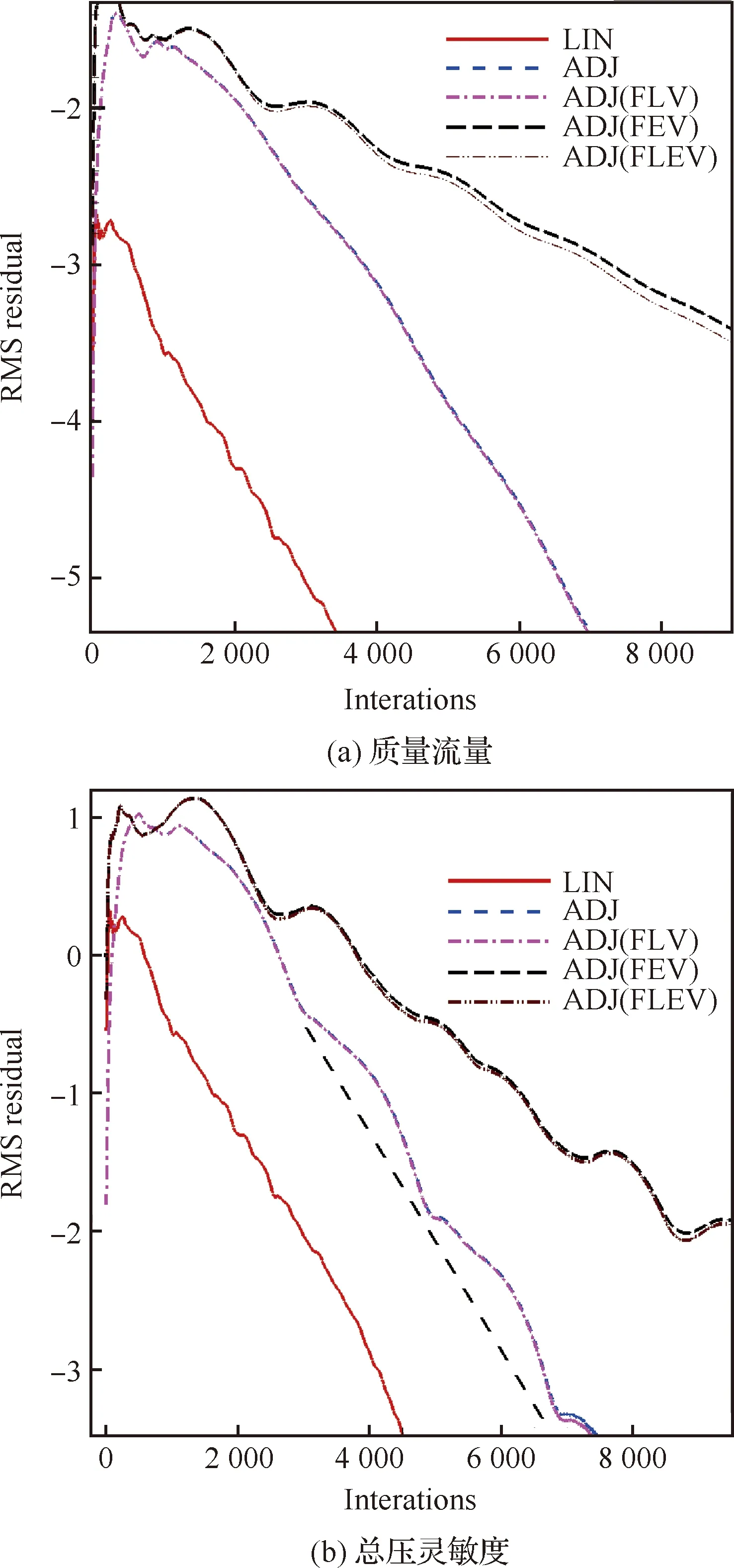
图16 最高效率点伴随求解器与线化求解器的残差收敛曲线Fig.16 Residual convergence histories of adjoint and linear solvers at a peak efficiency point

图17(a)和图17(b)分别为50%叶高处的层流黏性系数和湍流黏性系数云图。从图中可以看出，层流黏性系数的数值在10量级，并且变化范围较小(1.6×10～2.0×10)，而湍流黏性系数的数值更大(10量级)，变化范围也更广(0.001～0.01)。因而湍流黏性系数对总的黏性系数的贡献更大，影响也更大，验证了上述FEV比FLV对伴随灵敏度影响更大的结论。

图17 50%叶高层流黏性系数与湍流黏性系数云图Fig.17 Laminar and eddy viscosity coefficient contours at 50% span

5.1.4 计算时间及计算存储

图18对比了不同方法的计算耗时，横坐标为迭代步数，纵坐标为计算时间。从图中可以看出，所有伴随求解器的计算时间和存储消耗都高于LIN。其中，ADJ(FEV)的计算时间和存储消耗要低于ADJ(FLV)(见表4)。这是因为湍流黏性系数的计算牵扯到湍流模型方程的求解，计算存储和计算时间消耗更大，冻结湍流黏性系数将节省更多的计算存储和计算时间。

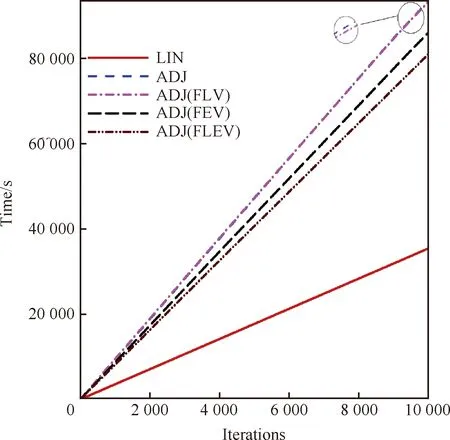
图18 伴随求解器与线化求解器计算耗时对比Fig.18 Comparison of computational cost between adjoint and linear solvers

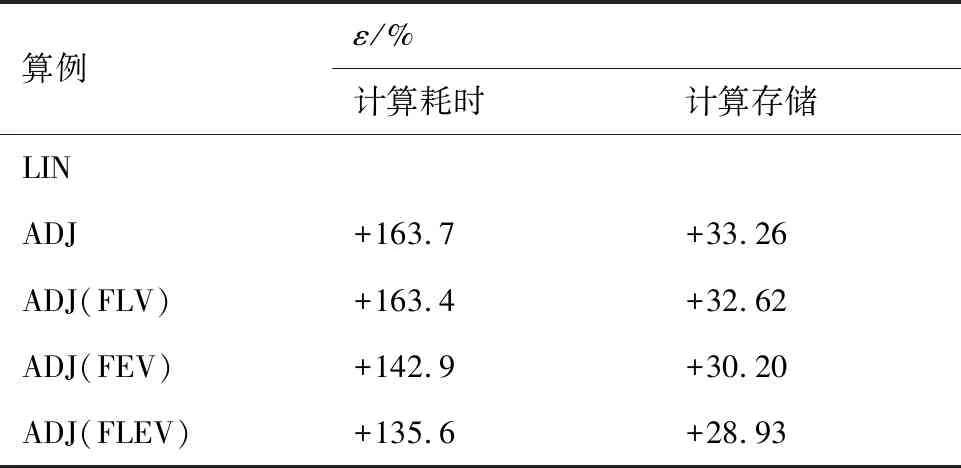
表4 伴随与线化求解器的计算耗时及计算存储对比

5.2 近失速点

图19给出了近失速点98%叶高处的相对马赫数云图。相较于最高效率点，近失速点的流场更加复杂。不仅有激波的存在，而且大攻角导致吸力面产生较大流动分离。这种同时具有强非线性和流动分离的复杂流场能更进一步验证湍流伴随求解器的有效性及鲁棒性。

图19 近失速点98%叶高处的相对马赫数云图Fig.19 Relative Mach number contours at 98% span near the stall point

为了节省空间，接下来只针对总压灵敏度展开分析。近失速点，伴随求解器与线化求解器的残差收敛曲线如图20所示。与设计点相同，ADJ与LIN具有相同的残差渐近收敛率，并且FLV对计算结果影响较小。不同于设计点，在近失速点采用FEV将直接导致计算结果发散。图21给出了伴随求解器与线化求解器的灵敏度收敛曲线。ADJ(FEV)和ADJ(FLEV)的灵敏度都未收敛，而ADJ与LIN的灵敏度收敛曲线吻合度非常高，相对误差为0.10%，稍高于最高效率点的0.07%。这进一步验证了湍流伴随求解器的有效性及鲁棒性，也说明了在伴随求解器开发过程中，考虑湍流黏性系数的微分可以增加伴随求解器的鲁棒性。

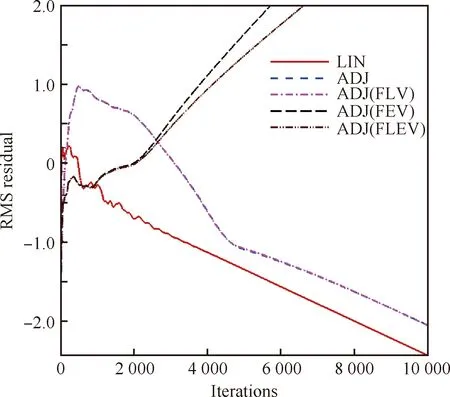
图20 近失速点伴随求解与线化求解器残差收敛曲线Fig.20 Residual convergence histories of adjoint and linear solvers at a near stall point

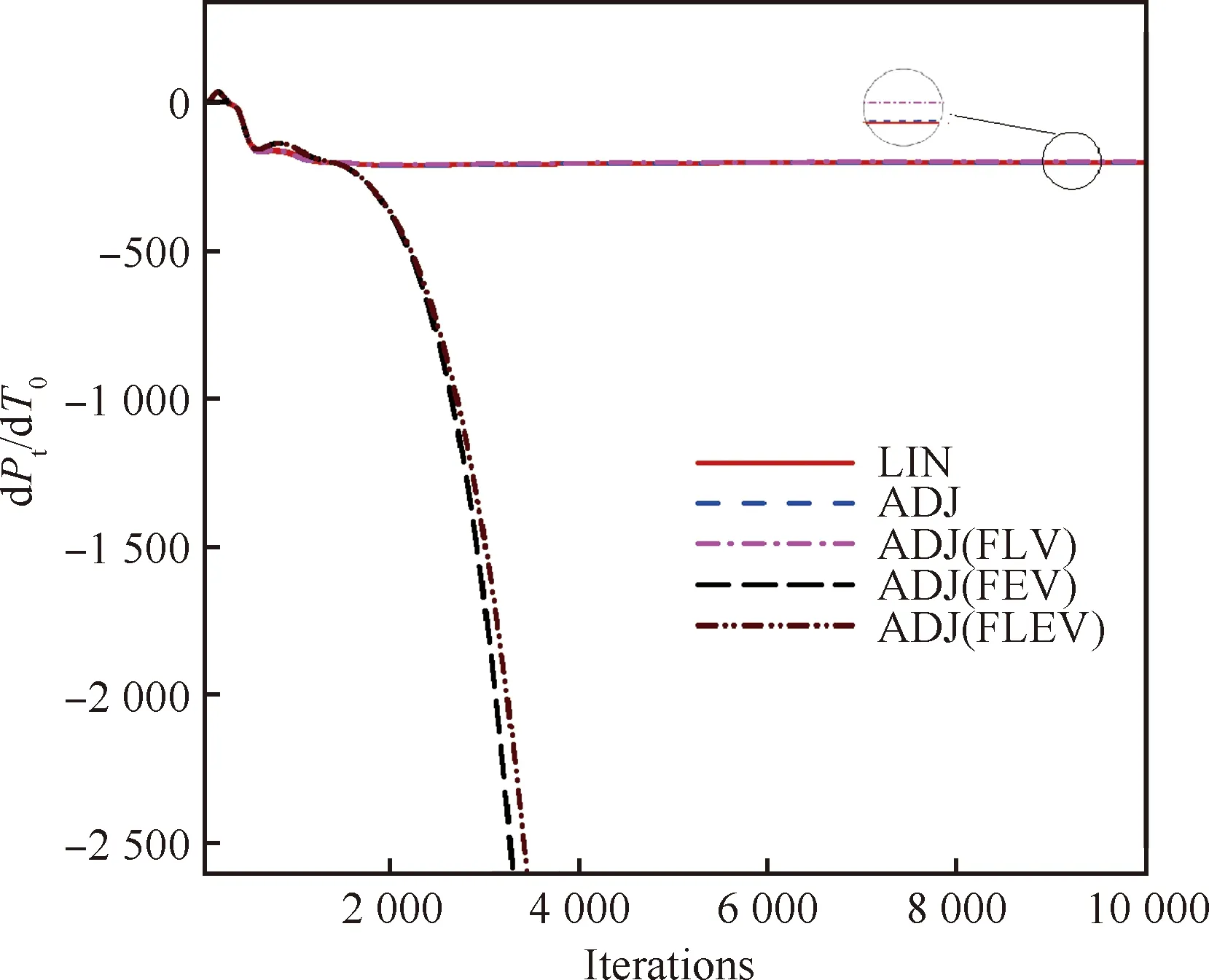
图21 近失速点伴随与线化求解器灵敏度收敛曲线Fig.21 Sensitivity convergence histories of adjoint and linear solvers at a near stall point

6 结 论

本文采用自动微分技术开发全三维湍流离散伴随求解器，并给出相应的流程图。不仅详细推导了完全湍流和3种不同定黏方法的伴随方程，而且介绍了伴随求解器每一个微分子程序的功能及手动组装这些微分子程序的过程。最后以NASA Rotor 67为研究对象，分别在最高效率点与近失速点研究了定黏方法对离散伴随系统的灵敏度精度、灵敏度收敛性及残差渐近收敛率的影响，并与完全湍流伴随求解器及线化求解器的结果进行对比，得到的结论如下：

1) ADJ与LIN具有一致的灵敏度收敛曲线及相同残差渐近收敛率。无论是线性目标函数还是非线性目标函数，相对误差都不超过0.10%。

2) “定黏假设”方法会影响伴随求解器的灵敏度精度及收敛性，并且FEV的影响大于FLV，前者对灵敏度的影响超过5%，而后者的影响低于1%。

3) “定黏假设”方法会影响伴随求解器的残差渐近收敛率，并且FEV的影响远大于FLV。在最高效率点，FEV和FLEV会使得伴随求解器的残差收敛变慢；在近失速点，FEV和FLEV将直接导致伴随求解器的计算结果发散。

4) 相比于ADJ，由“定黏假设”方法得到的伴随求解器在计算时间和计算存储消耗方面具有一定的优势，但是仍然远高于LIN。

致 谢

感谢课题组张倩为本文提供NASA Rotor 67的几何数据及实验数据。