基于机器视觉的立铣刀几何与状态参数在机检测

刘占，张俊，尹佳，赵万华

西安交通大学 机械制造系统工程国家重点实验室，西安 710054

航空结构件品种多且结构复杂，因此加工过程换刀频繁，装夹状态也时常变化，当下企业日益实行产线制，一个配刀工程师负责一条甚至多条产线刀具装库，不可避免会出现刀具参数装错，使得工艺要求刀具与实际安装刀具参数不符，如选用刀具直径不对、刀具悬长错误等，导致零件精度得不到保证甚至报废，造成巨大经济损失的同时延长了航空结构件生产周期。因此，很多企业在加工现场会增加一道人工刀具检测工序来保证生产安全，不但提高了人员成本，而且仍然面临着装刀参数错误问题。

随着视觉测量技术快速发展，国内外学者一方面研究视觉测量算法的高效性和鲁棒性，一方面将其应用于工程实践。Kassim等通过采用图像径向分割技术提高刀具参数检测精度。Jing为了解决螺纹几何误差测量中手动操作和检测效率低的问题，采用视觉和光学放大来测量螺纹的高精度几何误差。Yuan等建立了一个焦距变化系统，对圆头刀具进行三维测量，并利用该系统在一次测量中获得多个几何参数，并详细讨论了几何参数的类型和提取过程。刘今越等采用面结构光投影法对高效切削刀具的几何参数进行非接触式测量。尚波等搭建一套专用的回转体刀具在机测量系统，提供了实时的刀具数据便于加工现场的及时处理。侯秋林等提出一种连通域外接矩形刀具几何参数检测算法，开发基于机器视觉刀具几何参数在位快速检测系统。然而，上述算法只考虑了刀具直径和悬长测量，且只能在特定条件下获得较好的测量结果，要实现高效、全面的刀具几何参数在机测量，仍需进一步提高刀具轮廓提取精度、简化算法和提高设备测量精度。

以航空结构件加工应用最为广泛的整体式立铣刀为例，采用机器视觉测量系统采集刀具图像，针对立铣刀结构复杂的特点，采用基于立铣刀转动状态下的动态图像轮廓提取算法提取刀具轮廓。在此基础上研究刀尖圆角、直径以及悬长这3个最重要参数的视觉测量算法，通过多次试验验证了算法的准确性和测量系统的稳定性。

1 检测原理与方案

整体式铣刀结构复杂，直接对静态刀具采集图像如图1(a)所示，结果不确定性过大，不易提取刀具几何特征。采集刀具动态图像，逐帧进行轮廓提取，提取后的图像轮廓依序叠加来获取刀具几何特征。图像叠加原理表达式为

=×+×+

(1)

式中：为叠加后图像；和为原始图像；和为两图像的权值；为加到权重总和上的标量。

每一帧图像经轮廓提取后，通过式(1)叠加，结果如图1(b)所示，为直径；为悬长；为圆角半径。

采用如图2所示自动化刀具图像采集装置实现刀具动态图像采集。装置采用大尺寸后置背光源以及为相机一配用物距较大的镜头来获取刀具悬长整体图像信息，采用小尺寸背光源并为相机二配用物距较小的镜头来获取刀尖部分局部图像信息，既可以保证悬长测量范围足够大，又可以获得高质量刀尖圆角局部图像，刀具经背光源照射后成像如图3所示。

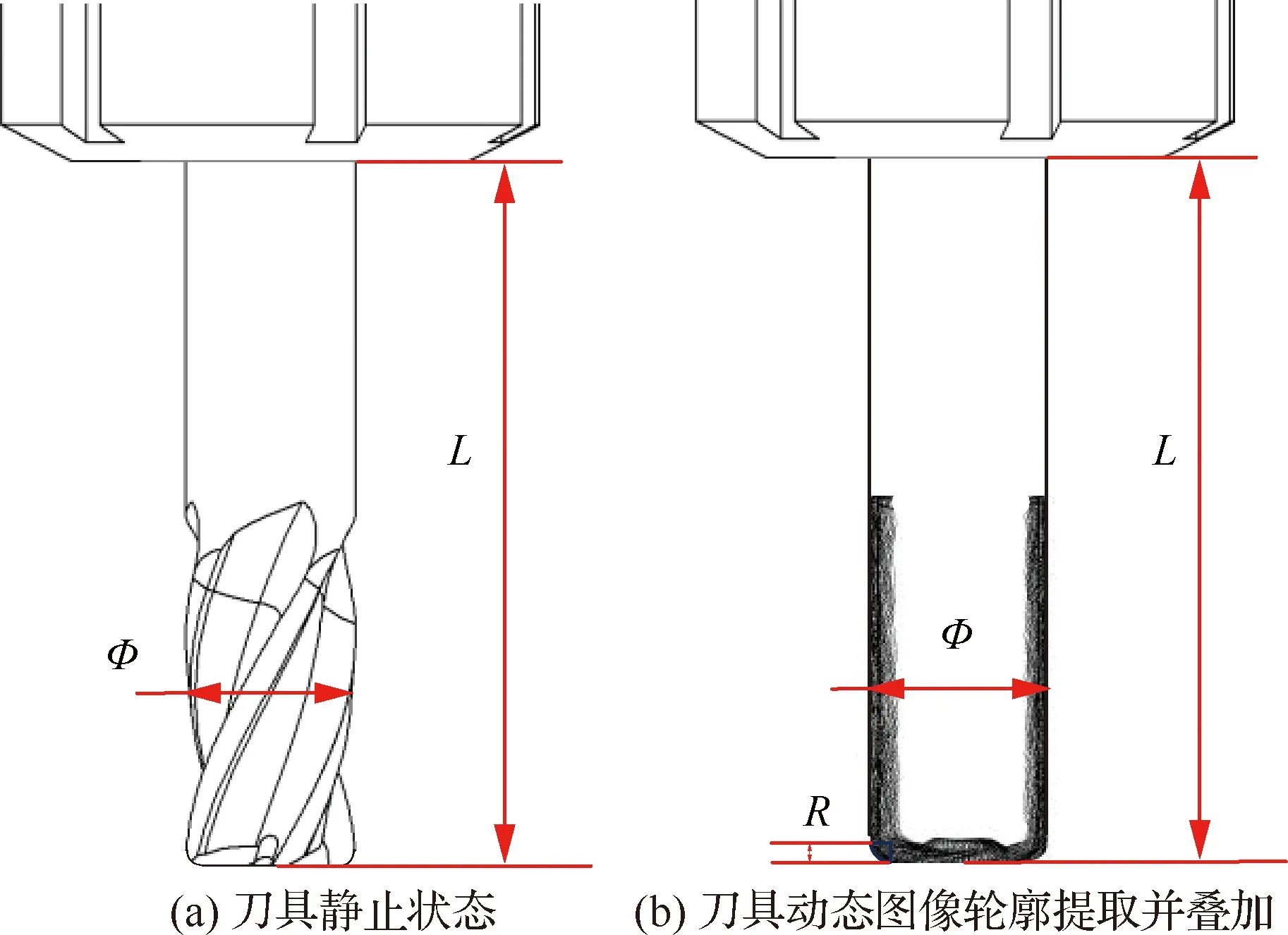
图1 刀具图像叠加前后对比Fig.1 Comparison of tool static image and tool overlay image

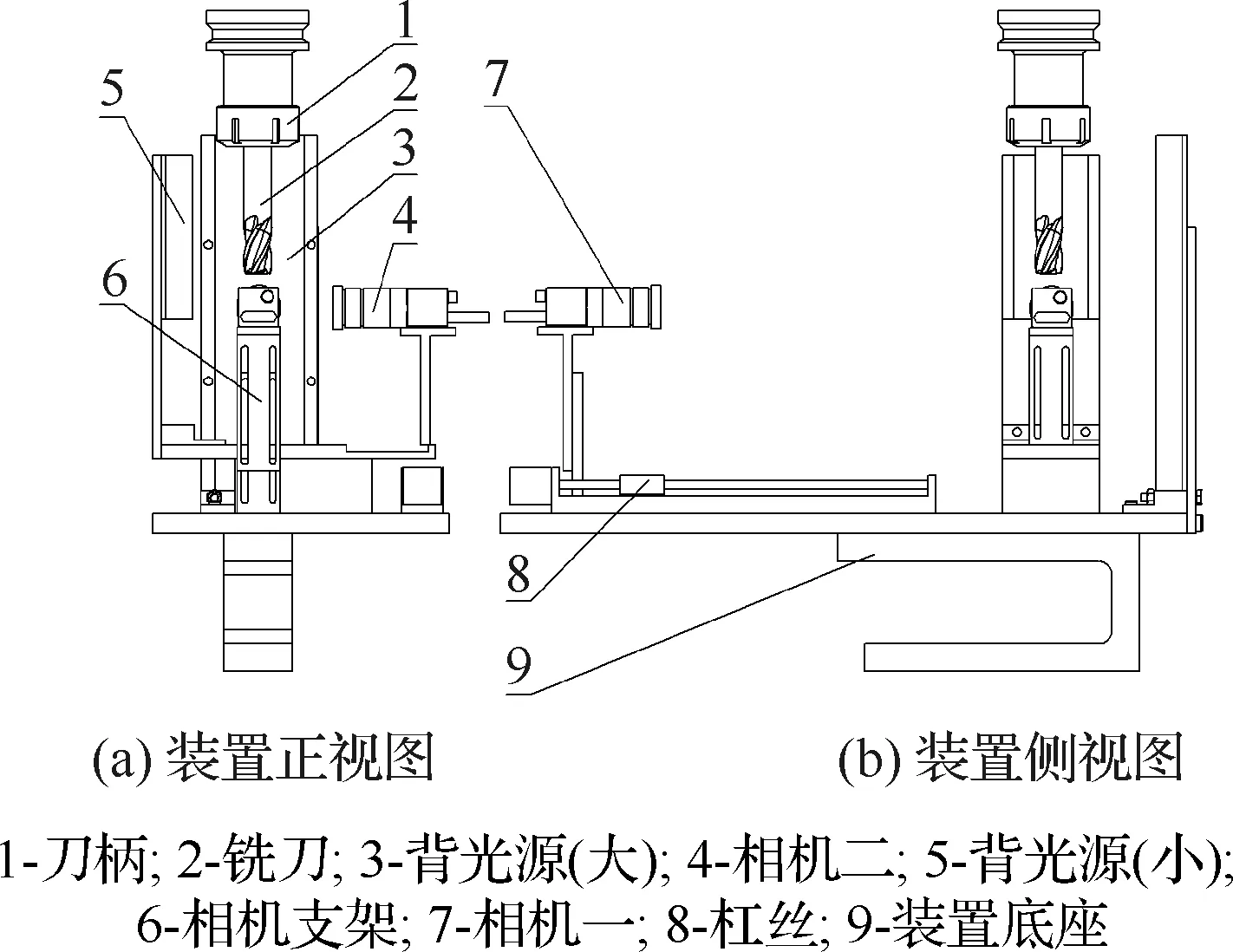
图2 刀具图像采集装置结构示意图Fig.2 Illustration of tool image acquisition device

图3 背光源照射下采集的刀具实际图像Fig.3 Tool image acquired under backlight

2 刀具几何与状态参数测量

2.1 刀尖圆角半径测量

该环节测量关键在于刀尖圆弧自动提取，相机二采集刀具动态图像，图像经自适应Gauss滤波、二值化后得到预处理图像，预处理图像经过边缘提取并依序叠加后得到轮廓叠加图像如图4所示。

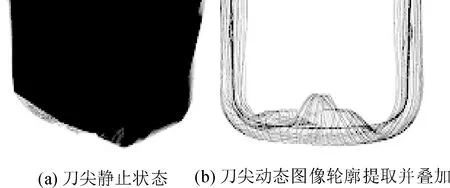
图4 刀尖图像叠加前后对比Fig.4 Comparison of tool tip static image and overlay image

为了在轮廓叠加图像上提取刀尖外轮廓，通过遍历扫描，得到刀尖外轮廓如图5(a)和图5(b)所示。利用霍夫变换粗略确定圆心位置，求所有外轮廓点距此圆心的距离，去除偏离圆心较大的点从而将不属于圆上的轮廓点剔除，得到刀尖圆弧如图5(c)和图5(d)所示。刀尖圆弧经最小二乘拟合得到拟合圆如图6所示，拟合圆半径即为刀具圆角大小。

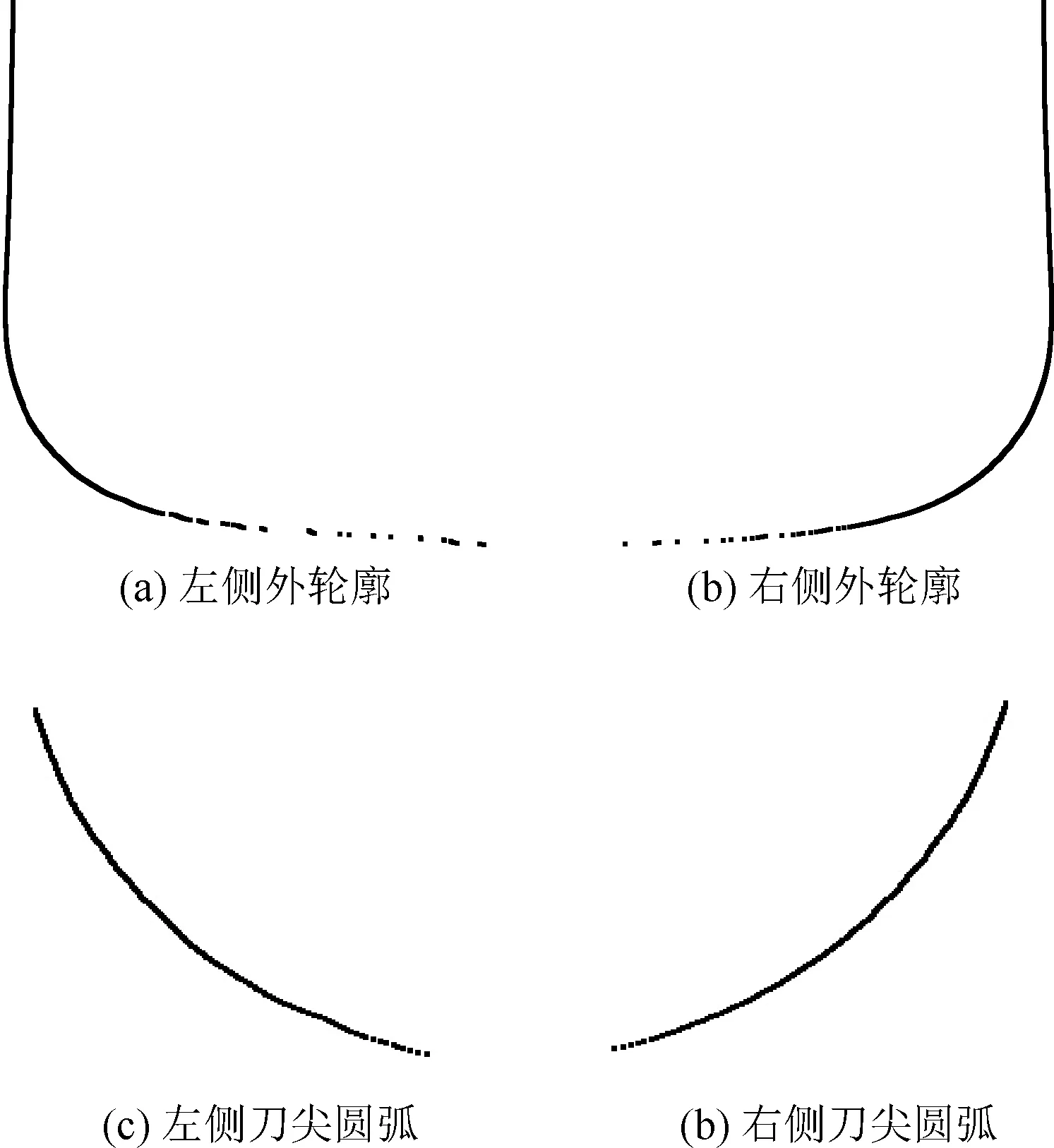
图5 刀尖圆弧提取Fig.5 Extraction of tool tip arc

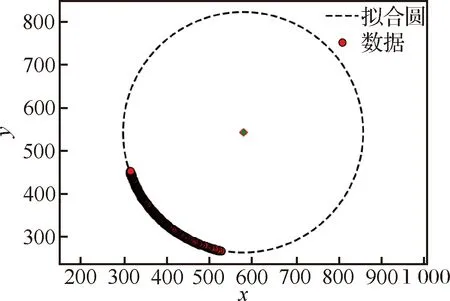
图6 刀尖圆弧拟合结果Fig.6 Fitting result of tool tip arc

2.2 刀具直径测量

刀具直径测量是将刀具轮廓叠加图像逐行扫描，提取刀体左右侧边界位置。刀具经背光源照射后相机所获取图像如图7(a)所示。

测量原理：逐行扫描轮廓叠加图像提取刀具左侧边界点，通过多次试验确定刀柄和刀体分界处的纵坐标值，即阈值，将图像上小于该值的像素点去除，得到刀体左侧边界点，并统计其横坐标的众数，将其视为基准，进而剔除偏离基准过大的点，取其余点横坐标的均值为刀具左侧边界位置，同样确定刀具右侧边界位置。

通过外接矩形将刀体部分包起来，此最小外接矩形的宽即刀具直径大小，直径测量如图7所示，刀具直径测量算法流程如图8所示。

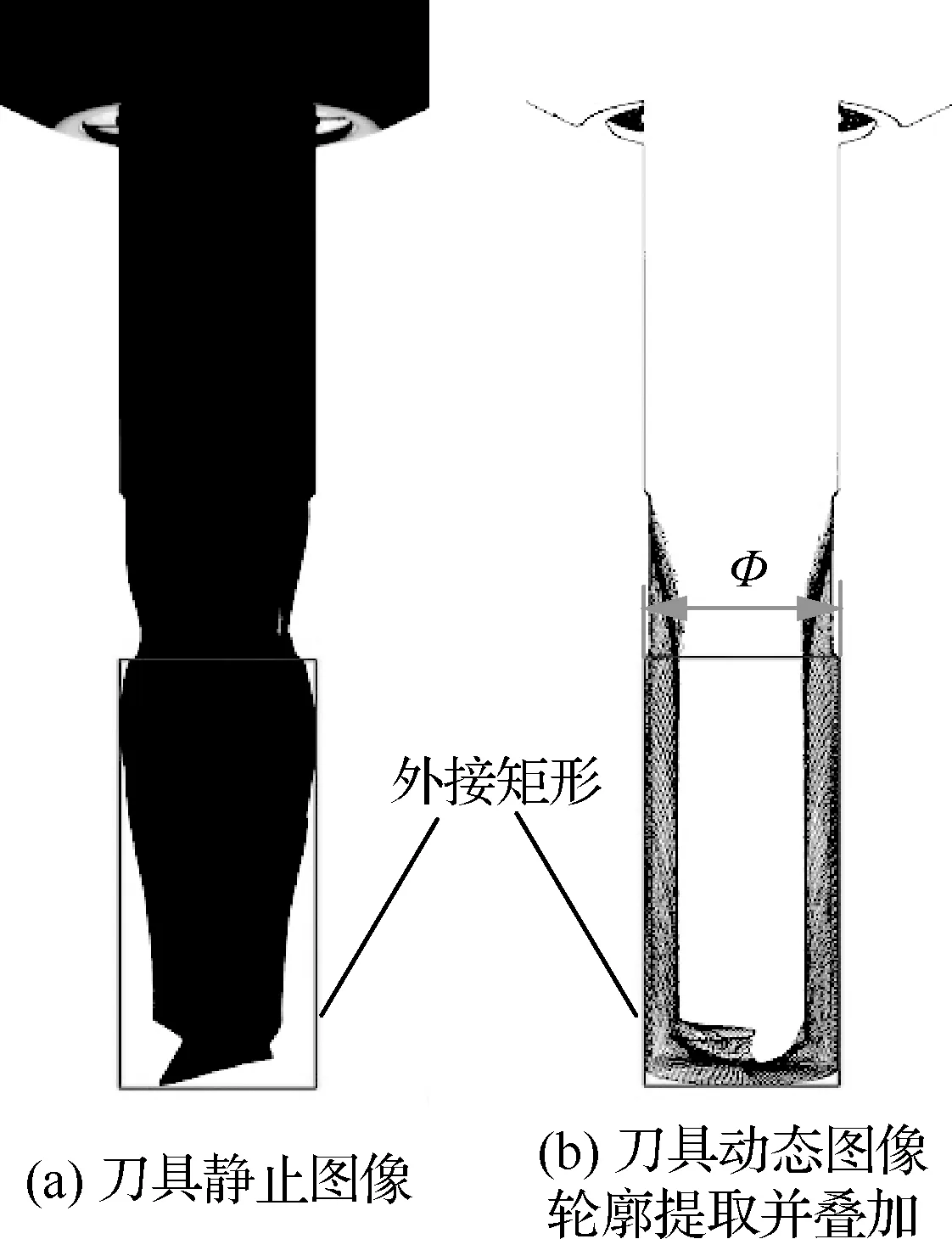
图7 刀具直径测量示意图Fig.7 Illustration of measurement for tool diameter

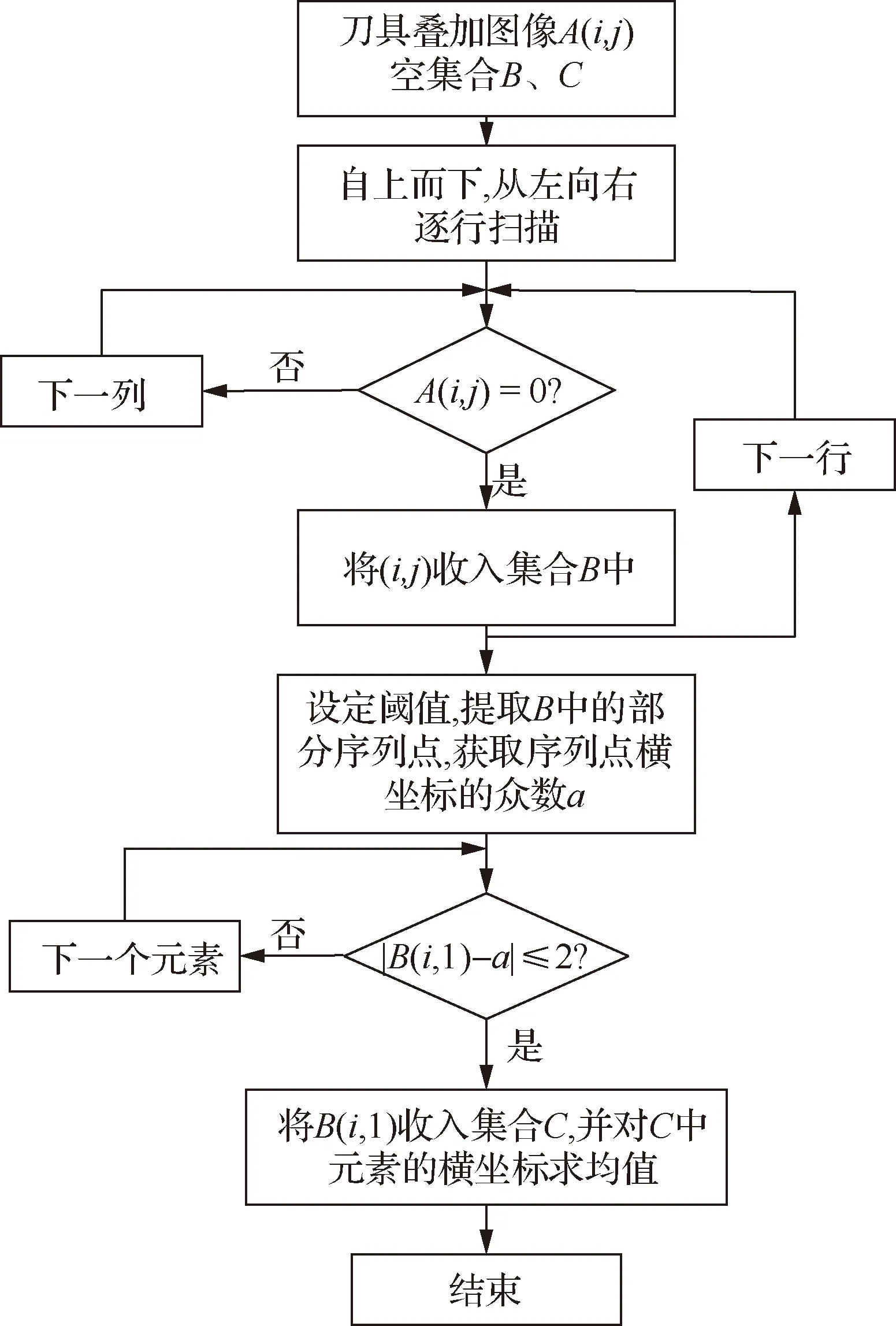
图8 刀具直径测量算法流程图Fig.8 Flow chart of detection algorithm for tool diameter

2.3 刀具悬长测量

提出了一种结合弧段提取与霍夫变换椭圆检测方法如图9所示。刀具悬长测量关键在于刀柄底端位置和刀尖点位置确定，利用两个位置纵坐标做差即为刀具悬长。刀具动态图像依序轮廓提取并叠加如图9(a)所示。

在实际试验中发现由于相机视野大，刀柄底端成像为椭圆状，所以通过椭圆拟合来对刀柄底端定位，拟合后椭圆中心的位置即为刀柄底端所在位置。

检测原理：采用自上而下逐列扫描策略从刀具轮廓叠加图上提取拟合候选曲线如左图9(b)所示。利用一系列直线段对曲线进行逼近得到一组直线段,,,…,，表示第条直线和第+1条直线之间夹角如左图9(c)所示，如果接近于0，说明第点处于一条近似直线上，将该点剔除，剩下平缓变化的点即为椭圆上点如左图9(d) 所示，最后通过霍夫变换求出椭圆中心点坐标。

刀尖点位置的确定主要通过自下而上逐列扫描轮廓叠加图像获取刀具底端轮廓序列点，统计出所选序列点中纵坐标最大点即为刀尖点。刀具悬长测量结果如图10所示。

图9 椭圆弧段提取示意图Fig.9 Illustration of ellipse arc extraction

图10 刀具悬长测量示意图Fig.10 Illustration of measurement for tool overhang length

2.4 悬长测量结果修正

实际测量悬长时发现由于刀具高度远大于透镜直径，根据透镜成像原理，柱体端部成像呈弧线状如图11所示，为镜头视野内柱体底面离透镜中心最远的点；为镜头视野内柱体底面离透镜中心最近的点；为透镜焦点；为焦距；为像距；为物距。由图11可以看出在成像平面上，柱体底面上的和两点所成像′和′不在同一水平位置上，′和′的垂直距离即为刀尖点的成像偏差。

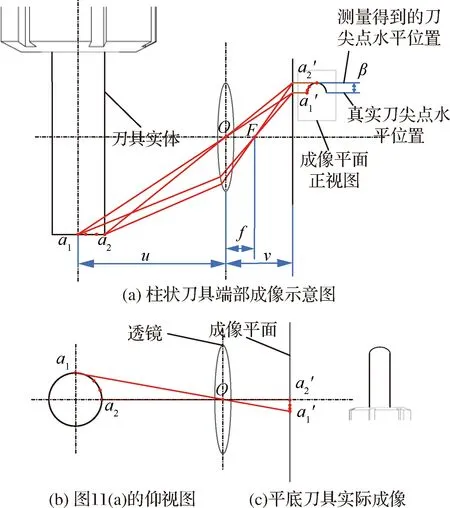
图11 刀尖点偏差示意图Fig.11 Illustration of tool tip point deviation

图像上刀尖点偏差反映到刀具实体上如图12 所示，由Δ∽Δ知图像上刀尖点偏差值反映到刀具实体上为，两者间关系为

=

(2)

式中：为Δ和Δ相似比；为刀具图像上刀尖点偏差值；为刀具实体上刀尖点偏差值。故通过计算图像上刀尖点的偏差可得到刀具悬长实际测量时的偏差。

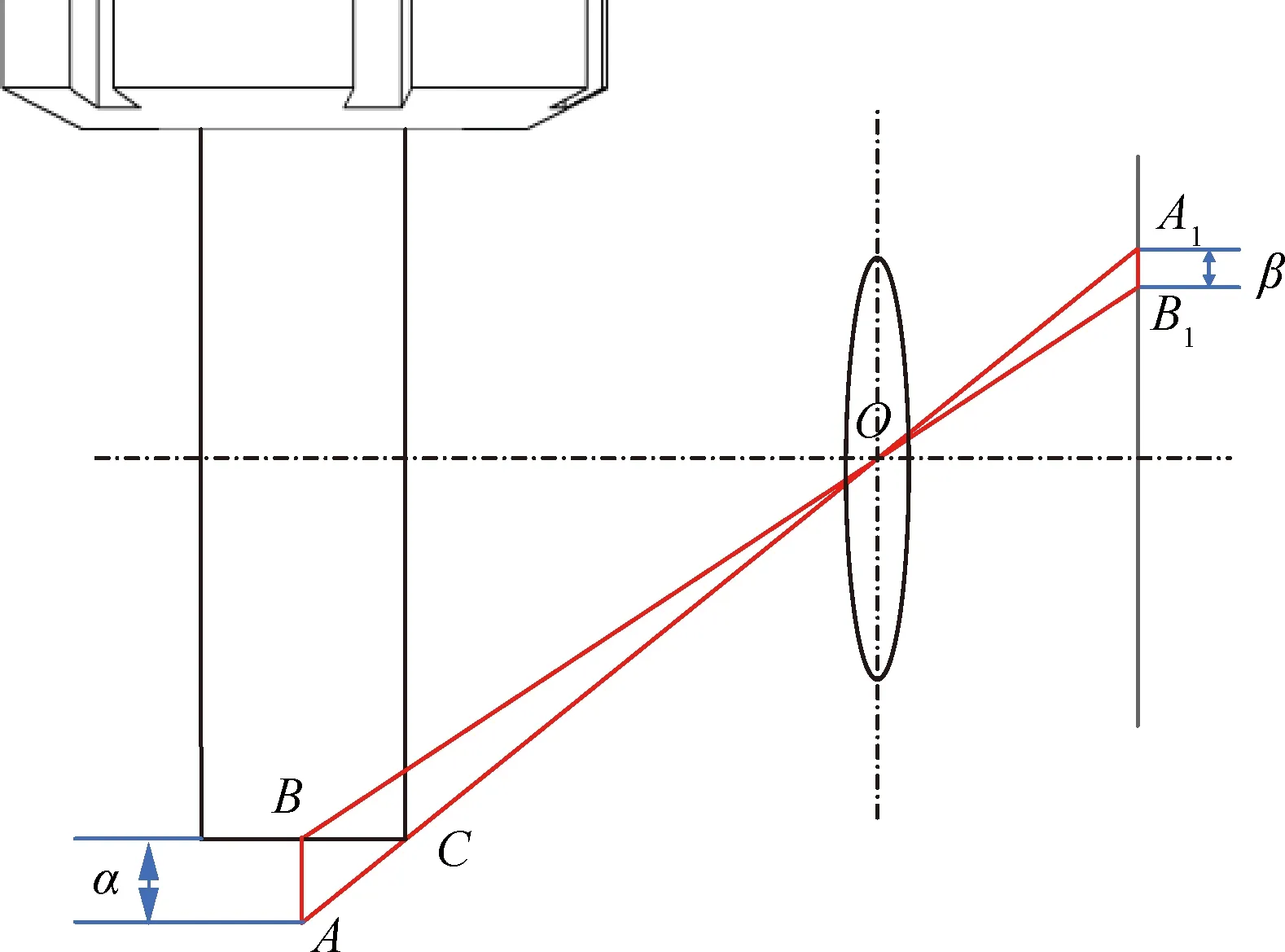
图12 图像上偏差反映到刀具实体上示意图Fig.12 Illustration of deviation in image reflected on tool entity

在本文试验条件下，当刀具悬长大于60 mm时会出现刀尖点偏差，本文选定悬长为80 mm，直径为20 mm平底铣刀作为标定刀具，将标定刀具实际偏差值设定为基准，求得修正公式对实际测量时刀具刀尖点位置偏差进行修正，具体分以下3种情况进行讨论。

1) 情况1：同直径不同悬长情况下刀尖点偏差对比如图13所示，黑色刀具为标定刀具；灰色刀具为待测刀具；为透镜中心与刀具的水平距离；为透镜中心与刀柄底部垂直距离；和为两刀具修正前悬长测量值；和为两刀具半径且=；和为两刀具刀尖点偏差值。

图13 同直径不同悬长刀尖点偏差对比Fig.13 Comparison of tool tip point deviation of different overhangs with same diameter

黑色刀具刀尖点偏差值可由Δ∽Δ求得，灰色刀具刀尖点偏差值可由Δ∽Δ求得：

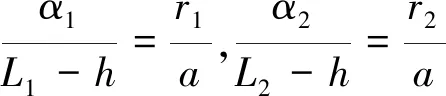
(3)

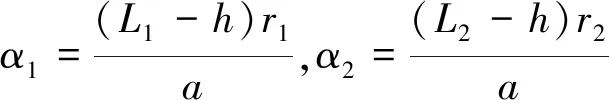
(4)

故同直径不同悬长情况下，灰色刀具刀尖点偏差值与黑色刀具刀尖点偏差值之比为

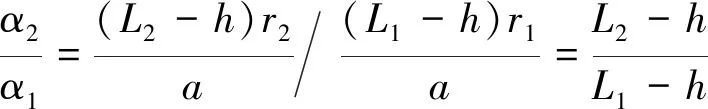
(5)

2) 情况2：同悬长不同直径情况下刀尖点偏差对比如图14所示，为黑色刀具直径；为灰色刀具直径。和的计算同式(3)和式(4)。

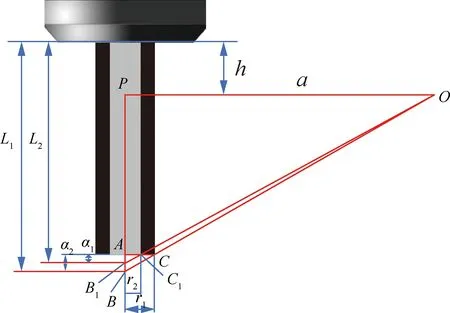
图14 同悬长不同直径刀尖点偏差对比Fig.14 Comparison of tool tip point deviation with the same overhang length and different diameters

故同悬长不同直径情况下，灰色刀具刀尖点偏差值与黑色刀具刀尖点偏差值之比为

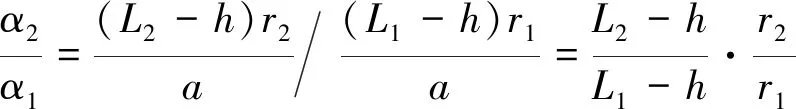
(6)

3) 情况3：同直径不同悬长有无圆角情况下偏差对比如图15所示，黑色刀具为标定刀具；灰色刀具为待测刀具；为灰色刀具刀尖圆角半径；为透镜中心与刀具的水平距离；为相机中心与刀柄底部垂直距离；和为两刀具修正前悬长测量值；为两刀具直径。夹角和的表达式为

(7)

黑色刀具刀尖点偏差值：

(8)

灰色刀具刀尖点偏差值：

==tan·

(9)

(10)

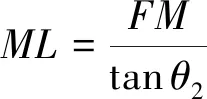
(11)

=-+

(12)

故：

(13)

化简得：

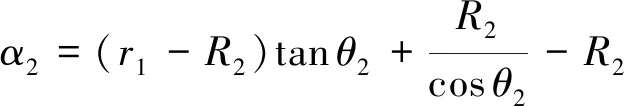
(14)

图15 同直径不同悬长有无圆角情况下刀尖点偏差对比Fig.15 Comparison of tool tip point deviation with the same diameter and different overhangs and whether having arc

同直径有无圆角情况下，灰色刀具刀尖点偏差值与黑色刀具刀尖点偏差值之比为

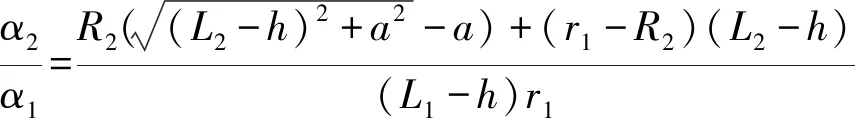
(15)

以黑色平底铣刀为标定刀具，先求出悬长、半径为标定刀具的测量悬长和刀尖点偏差值。然后测量其他刀具时测量得到该待测刀具悬长的测量值。

最后综合上述3种情况的结论式(5)和式(6)以及式(15)可知考虑悬长、直径、圆角都不同情况下，该待测刀具刀尖点偏差值为

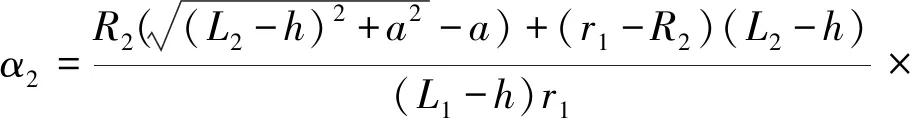
(16)

将该待测刀具悬长测量值减去刀尖点偏差值即为修正后该待测刀具悬长测量结果。

3 试验验证与分析

企业现场对刀具悬长和直径的测量误差要求不超过0.1 mm，刀具圆角的测量误差要求不超过0.05 mm。试验方案选用两台相机均为型号acA4024-29 μm的工业相机，最大分辨率为4 024(pixel)×3036(pixel)，同时为采集刀具悬长和直径图像的相机配用型号M0814-MP2(CH)3的镜头，为采集刀具刀尖局部图像的相机配用型号M0824-MPW2的镜头。

试验时将图像采集装置装在机床一固定位置，每次测量时通过数控系统设定主轴移动到该固定位置进行刀具参数测量如图16所示。每次测量所需时间包括主轴移动时间、刀具图像采集时间、图像处理程序运行时间等为10 s。

试验采集的像素阵列分辨率为相机最大像素分辨率4 024(pixel)×3 036(pixel)，像素阵列为灰度像素阵列。采集刀具动态图像时，为了保证可以更准确的获得刀具轮廓，必须使相机每获取一帧图像时刀具所转过的角度足够小且每次获取的图像不重合，因此相机采样频率和刀具转速必须满足：

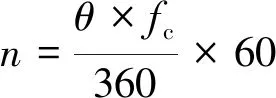
(17)

式中：为主轴转速；为相机采样频率；为每采集一帧图像刀具所转动角度。本试验条件下，刀具转速30 r/min；相机采样频率20 fps；每采集一帧图像刀具转角9°。

图16 刀具几何与状态参数检测装置Fig.16 Experimental device of tool geometry and state parameter detection

3.1 像素点标定

为将图像中点的二维像素坐标准确反映到真实世界中，必须预先对像素点大小进行标定，因为本文在检测时始终保持刀具与相机的水平距离固定，所以只需在装置使用前将像素点大小提前标定，通过黑白棋盘格标定板对像素点进行标定如图17所示。

标定板型号为CC-050-O-3，每个角点之间的真实距离为3 mm,首先提取棋盘格中的角点如图18所示。提取角点后可获得角点的像素坐标，由角点像素坐标的差值和实际距离即可求得单个像素点的所代表的实际尺寸。经过试验，相机1像素点大小标定为53.139 μm，相机2像素点标定为11.645 μm。

图17 像素点大小标定示意图Fig.17 Illustration of pixel size calibration

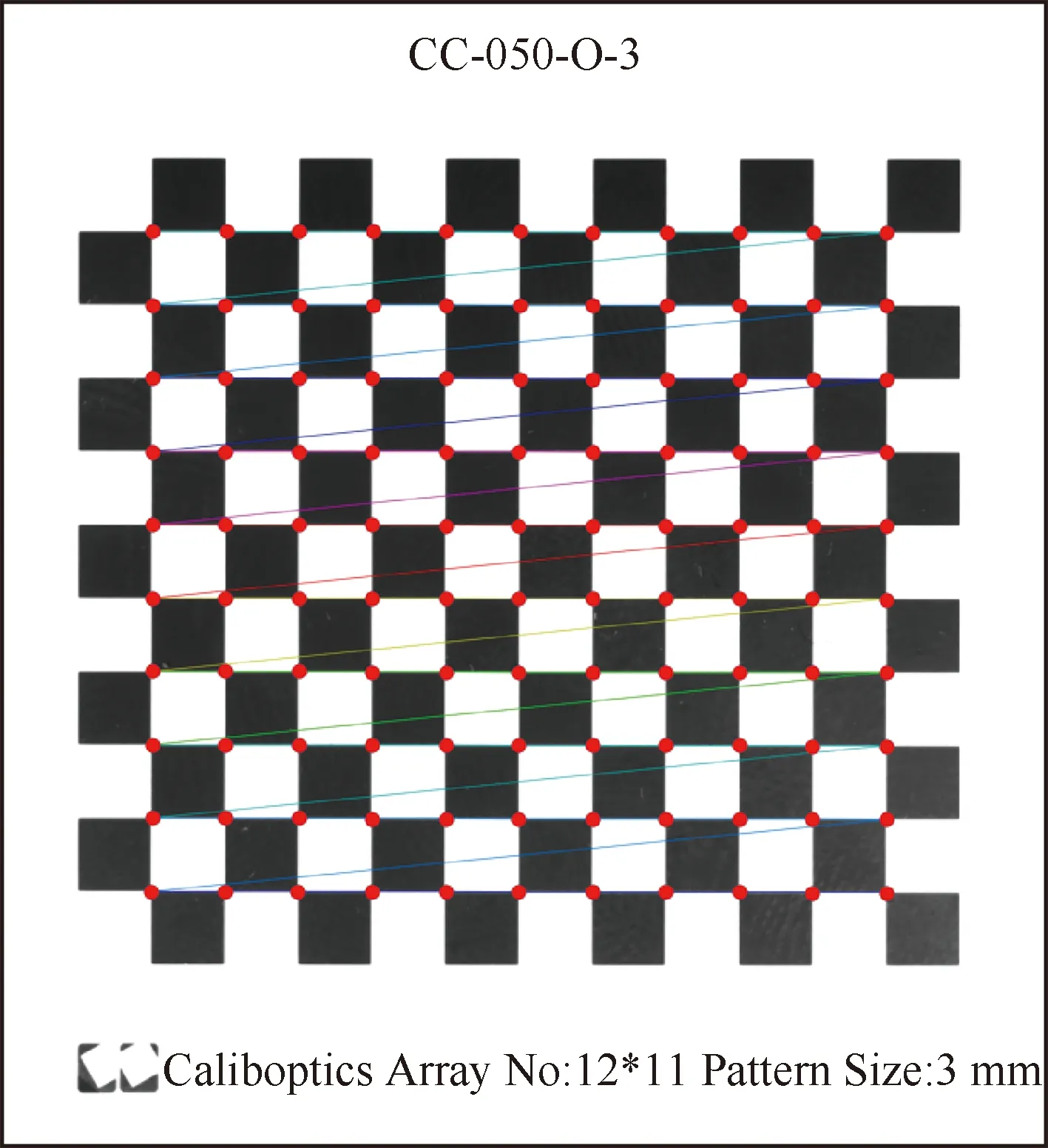
图18 角点提取结果Fig.18 Result of corner extraction

3.2 测量结果

对60组不同参数刀具进行图像采集，首先用螺旋测微仪测量刀具实际参数，接着将刀具装到机床上并获取刀具动态图像，然后通过前文研究的测量算法计算刀具的几何与状态参数，与相应人工实际测量值进行比较，其中选取8组刀具参数测量结果见表1。

60组不同参数刀具试验相对测量误差如图19 所示。可以得出，相对测量误差最大为0.51%，悬长测量误差<0.05 mm，直径和圆角测量误差<0.02 mm，满足刀具测量实际误差要求。

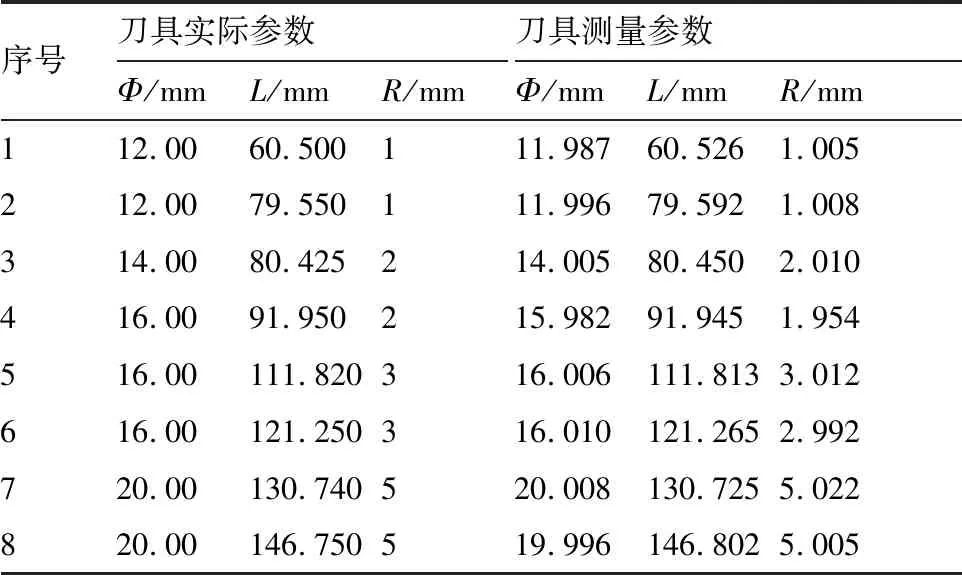
表1 刀具几何与状态参数测量结果

图19 刀具几何与状态参数相对测量误差Fig.19 Relative measurement error of tool geometric and state parameters

4 结 论

1) 分析了刀具动态图像成像特点，采用立铣刀转动状态下动态图像轮廓提取算法，解决了刀具圆角几何特征难以提取的问题。

2) 研究了刀具几何与状态参数测量算法，分析了影响悬长测量精度的因素，针对相机视野过大导致的悬长测量偏差问题，提出了偏差修正算法，提高了悬长测量精度。

3) 完成了刀具几何与状态参数在机检测装置测量试验，给出了刀具参数在机测量精度与误差范围，验证了刀具参数检测装置的精度和有效性。