考虑伴生转动的大行程柔性微定位平台

曹毅，孟刚，居勇健，徐伟胜

1. 江南大学 机械工程学院，无锡 214122 2. 江苏省食品先进制造装备技术重点实验室，无锡 214122

柔性机构是一类依靠材料弹性形变实现运动传递的新型机构，避免了刚性机构中的摩擦磨损，提高了运动定位精度；无需装配及润滑，降低了生产及维护成本。在航空航天领域，因其工作环境相对恶劣、不允许润滑剂及摩擦屑的存在，柔性机构得以广泛应用。在航天器微波天线对准机构、卫星光学器件姿态调整及空间在轨精细操作等对定位精度要求较高的领域，柔性微定位平台已成为空间精密定位的主要载体。

在精密定位领域，为满足高精度定位需求，常采用宏微双重驱动的方式，该方式要求微定位平台运动行程大于刚性机构的位移分辨率。因此，设计具有毫米级行程、微米级定位精度的柔性微定位平台是实现精密定位的关键。平台设计过程中，运动副串联及分布柔度式柔性单元可有效增加运动行程，但前者的误差累积和后者产生伴生转动均对其定位精度产生消极影响，对大行程微定位平台的优化设计和伴生转动研究及如何减小其消极影响已成为该领域一大研究热点。

Awtar等基于分布柔度式柔性薄板设计了一种运动解耦的大行程微定位平台，并指出伴生转动现象对其运动精度的消极影响。Hao采用分布柔度式细杆设计了3-PPPR(P、R分别表示平动、转动自由度)型微定位平台，对其伴生转动、耦合位移进行了分析；并基于刚度中心重合方法提出了一种低伴生转动的3-PPPRR型柔性微定位平台。Li等基于PRB模型设计并分析了一种新型五支链微定位平台，利用结构对称性消除了运动过程中产生的部分伴生转动。Kong和Hao基于反向串联方法提出了一种大行程微定位平台，从结构上优化了平台运动性能。Lin等基于运动副替换设计了一种低伴生转动的微定位平台，并进行了有限元仿真及实验测定。此外，Kim等通过优化设计方法，提出了一种伴生转角最小化的原子力显微镜扫描平台。

伴生转动是影响平台定位精度的重要因素。综合国内外研究不难发现，目前对平台伴生转动的研究多限于定性分析及结构改进，而对伴生转动的量化研究相对欠缺。基于此，本文针对大行程柔性微定位平台伴生转动问题进行了深入研究。首先，提出了一种具有大行程、高精度的5-PPPR型柔性微定位平台；其次，在考虑伴生转动情况下对其静、动态特性进行了理论建模，相较于不考虑伴生转动，输出位移理论误差降低了94.63%，大幅提高了平台理论精度；然后，基于有限元仿真验证了理论模型的正确性；最后，探究了柔性杆结构参数与平台性能的灵敏度关系，并基于分析结果对平台进行参数优化。

1 结构设计

1.1 PPR型柔性运动副设计

柔性微定位平台常采用结构紧凑且动态性能优越的并联式结构。采用分布柔度式柔性单元来满足平台大行程的需求，同时避免应力集中问题。为便于实现高精度位移控制，平台应具有低伴生转动和较好的运动及驱动解耦特性。

为此，首先基于分布柔度式柔性杆提出了一种PPR型柔性运动副如图1所示。PPR型柔性运动副采用反向串联方法，通过改变寄生运动的方向，在增大平台运动行程的同时，将两组四杆结构产生的寄生运动相互抵消(-)，提升了平台的运动精度及解耦特性，且该结构在承受径向载荷时，由于中间刚性平台的过渡作用，柔性杆不会产生轴向拉伸，避免了因轴向形变引起的柔性杆应力刚化效应，其工作原理如图2所示。

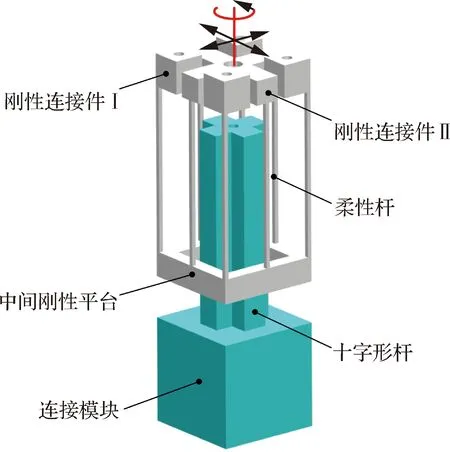
图1 PPR型柔性运动副Fig.1 PPR compliant joint

图2 PPR型柔性运动副工作原理Fig.2 Schematic diagram of PPR compliant joint

1.2 5-PPPR型柔性微定位平台设计

基于上述PPR柔性运动副设计的5-PPPR型柔性微定位平台如图3所示，包括、轴方向4个结构相同的支链一、轴方向支链二、动平台及基座。微定位平台采用结构对称的五支链布局，消除了动平台、方向的输入、输出耦合及方向运动时的伴生转动，其支链对称布局提高了平台定位精度，优化了平台运动性能。

图3 5-PPPR型柔性微定位平台Fig.3 5-PPPR compliant micro-positioning stage

支链一结构如图4(a)所示，包括4个相同的PPR型柔性运动副，其中3个并联连接构成支链的驱动副，其自由度等效为沿其正交方向具有平移自由度的P型运动副；并与正交方向被动副模块下端串联固接，构成PPPR型支链一整体。同理，支链二结构如图4(b)所示。基于螺旋理论，该平台自由度可表示为

2{,,,}∩2{,,,}∩{,,,}=

{,,}

(1)

图4 平台支链结构示意图Fig.4 Schematic diagram of kinematic limbs of stage

2 静、动态特性分析

2.1 刚度分析

刚度是指微定位平台在运动方向上产生单位位移时所需力的大小，是衡量平台静态特性的重要指标。考虑到运动副无应力刚化、可线性分析的特点，采用矩阵法对平台刚度进行分析。

对于一端固定的方形截面细长杆，其末端中心点处的力-位移关系柔度矩阵在小变形假设下可表示为

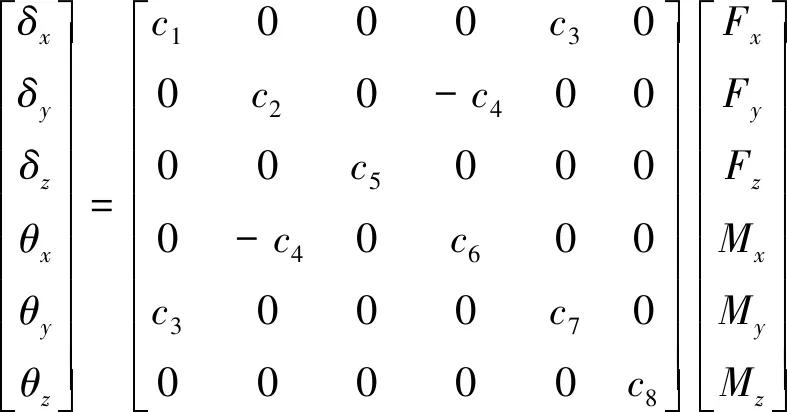
(2)

式中:、、、(=,,) 分别表示沿轴的广义驱动力和广义驱动位移;==4，==6，=，==12，=0.141;、分别为材料的弹性模量及剪切模量;、分别为梁的长度、厚度。

如图5(b)所示，在柔性杆及内四杆模块的自由运动端分别建立坐标系-、-，柔性杆～坐标系同理可建。基于矩阵坐标变换原则，运动副内四杆结构在坐标系-下的柔度矩阵可表示为

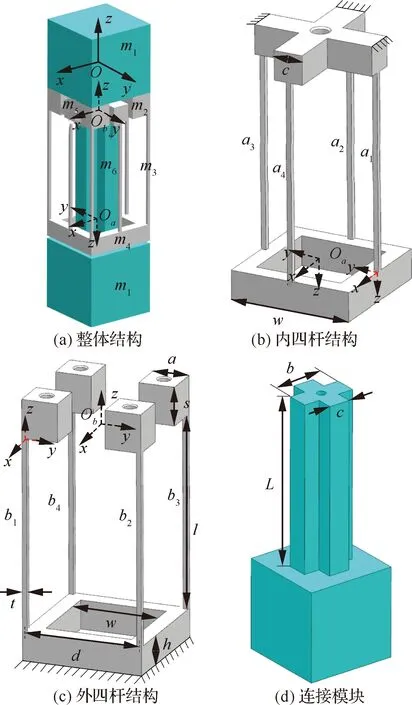
图5 柔性运动副结构示意图Fig.5 Schematic diagram of structural of PPR joint

(3)

如图5(c)所示，同理建立相应坐标系-(=1～4)及-，运动副外四杆结构在坐标系-下的柔度矩阵为

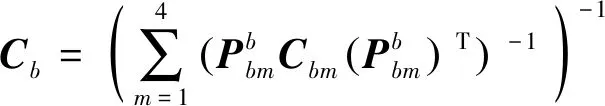
(4)

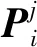
(5)

其中:、、为坐标系-到坐标系-的向量坐标。

将二者转换到坐标系-中，如图5(a)所示，则运动副在坐标系-下的柔度矩阵为

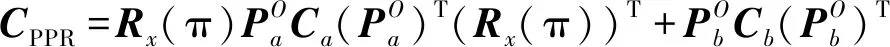
(6)

()为绕轴旋转角的旋转变换矩阵：

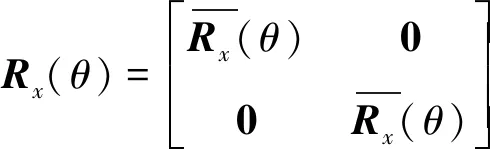
(7)

(8)

故PPR柔性运动副在-的刚度矩阵为

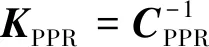
(9)

如图4(a)所示，对于平台、方向的支链一，其3个PPR运动副并联连接组成驱动副，被动PPR副与驱动副正交方向串联连接，故支链一驱动副在动平台中心-点处的柔度矩阵为

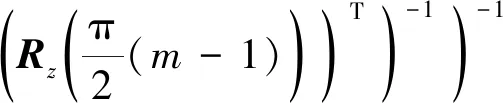
(10)

式中:为构成其驱动副的PPR型模块在-坐标系下的柔度矩阵：

(11)

故支链一在-点处柔(刚)度矩阵为

=P+

(12)

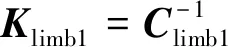
(13)

同理可求得沿方向支链二的驱动副及其整体在动平台中心坐标系-下的柔度及刚度矩阵分别为P、、P、。

5条支链与动平台为并联连接，故柔性微定位平台整体在动平台中心坐标系-下的柔度矩阵可表示为

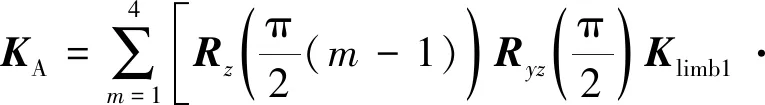
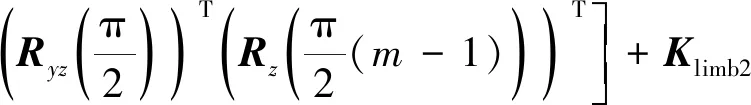
(14)

式中:()为分别绕轴、轴同时旋转角度的旋转变换矩阵：

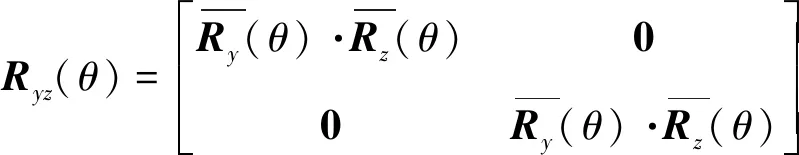
(15)

(16)

(17)

为进一步得到微定位平台各方向输入点处的刚度，需将所有柔性单元的柔度矩阵变换到各输入点。如图3所示，以-点处为例，设支链一主动副、支链一被动副及其余四条支链并联连接的整体在输入点处的刚度矩阵分别为1、2、3，则：

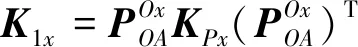
(18)

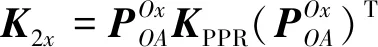
(19)

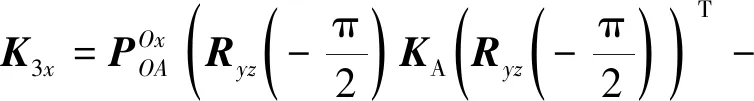
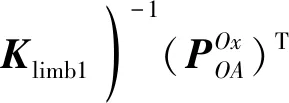
(20)

支链一主动副、支链一被动副及其余四条支链并联连接的整体相对该输入点串联连接，故平台在方向输入刚度矩阵表示为

=1+2+3

(21)

鉴于该平台结构的对称性，故其在、方向具有相同的输入刚度，即：

=

(22)

同理，根据支链串并联关系及矩阵变换规则可以求得支链二主动副、被动副及、方向四条相同支链一并联连接的整体在-输入点处的刚度矩阵1、2、3及平台方向输入刚度矩阵。

因此，平台的输入刚度为

(=,,)=[3,3]

(23)

2.2 伴生转动分析

对于空间平动微定位平台，在完成其主运动功能的同时，还会产生额外的转动，称之为伴生转动，其转角为伴生转角。伴生转动是导致平台定位精度降低的重要因素，应尽量减小。

2.2.1 PPR柔性运动副伴生转动

微定位平台工作状态下，PPR柔性运动副两组四杆结构受力和力矩情况不同，其伴生转动也相应不同，因此需分别进行分析。

1) 外四杆结构受力

假设柔性杆上端刚性连接平台具有绝对刚性，且在运动过程中不产生自身形变，柔性运动副外四杆结构～受水平力4产生形变简化示意图如图6所示。

外四杆结构末端平台受水平力4作用时，考虑柔性杆轴向变形，左侧柔性杆受拉力1拉伸，右侧柔性杆受压力2压缩，进而引起整体偏转，设该偏转角为，杆轴向形变量分别为Δ、Δ，如图6所示。鉴于其结构的对称性，作用于两侧柔性杆末端的力和力矩大小相同。故==、1=2=、==，则有：

(24)

图6 外四杆结构受水平作用力形变简化示意图Fig.6 Schematic diagram of deformation of external beams module exerted by a horizontal force

式中:为柔性杆杆间距；为柔性杆截面积。

基于固定导向梁的弯曲变形理论，结合图6柔性杆受力情况，其截面转角方程为

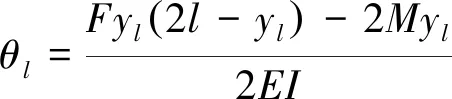
(25)

则柔性杆端截面转角为

(26)

联立式(18)和式(20)得：

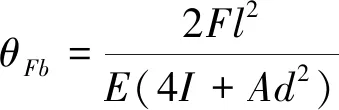
(27)

2) 外四杆结构受力矩

运动副外四杆结构受力矩4作用时，考虑柔性杆轴向形变，引起刚性连接平台整体偏转，设该转角为，如图7所示，有1=2=、==，则其形变及力偶平衡关系可表示为

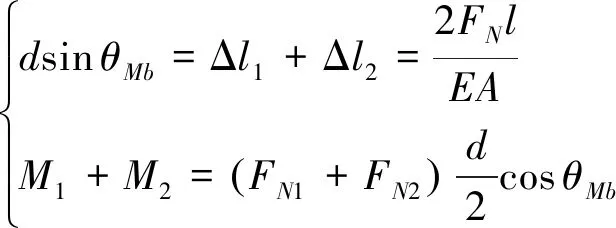
(28)

联立可得：

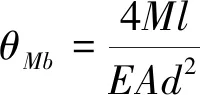
(29)

3) 内四杆结构受力

柔性运动副内四杆～受水平力4作用示意图如图8所示，将该作用力分解为两正交方向分力、分别作用于边长为'的等效立方体(图示虚线)侧边处，并将、转化到′和′作用点处，随之产生两附加力矩、，则有：

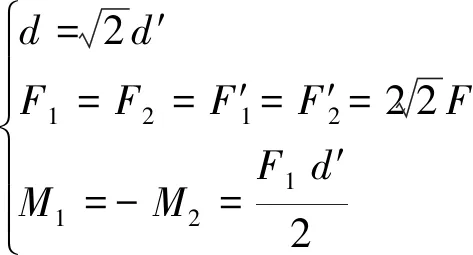
(30)

图7 外四杆结构受力矩形变简化示意图Fig.7 Schematic diagram of deformation of external beams module subjected to a moment

图8 内四杆受力形变简化示意图Fig.8 Schematic diagram of internal beams module exerted by a horizontal force

内四杆结构受作用力4产生伴生转动效果与受力′、′及力矩、共同作用效果等价。其中′、′对边长′的等效立方体作用效果与上述外四杆结构受力偏转原理一致。基于式(24)～式(27)同理可得等效立方体平台在力′、′作用下，产生的伴生偏转角、为

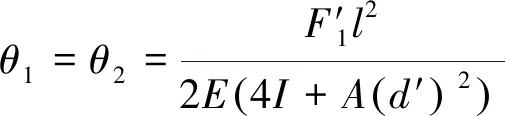
(31)

附加力矩、大小相等、方向相反，其对平台产生的伴生转动相互抵消，不予考虑。

基于几何关系可得，内四杆结构受力4作用产生的沿该力方向的偏转角为

(32)

4) 内四杆结构受力矩

内四杆结构受力矩4作用时，考虑柔性杆轴向变形，引起刚性平台整体偏转角设为，如图9所示，其形变及力偶平衡关系式为

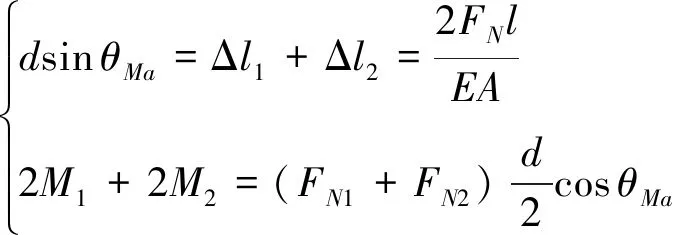
(33)

基于式(33)可得：

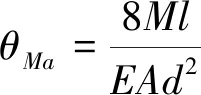
(34)

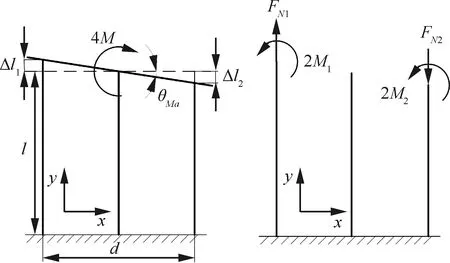
图9 内四杆结构受力矩形变简化示意图Fig.9 Schematic diagram of deformation of internal beams module subjected to a moment

必须指出的是，用于固定柔性运动副的连接模块(图5(d))运动过程中也会产生微量偏转：

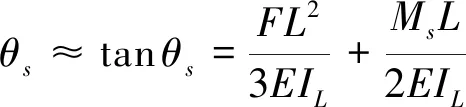
(35)

式中:为十字形杆长度;为其截面惯性矩;为附加力偶矩。

PPR柔性运动副末端平台受力4作用时，各部分结构受力及偏转效果如图10所示，运动副总伴生转角为以上各作用效果的累加，即

=+-++

(36)

式中:、和中附加力偶矩分别为

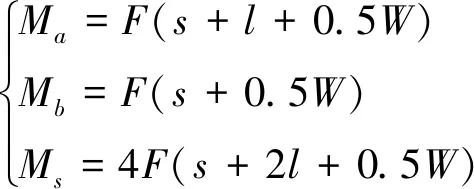
(37)

其中:、、为运动副结构参数，详见图5。

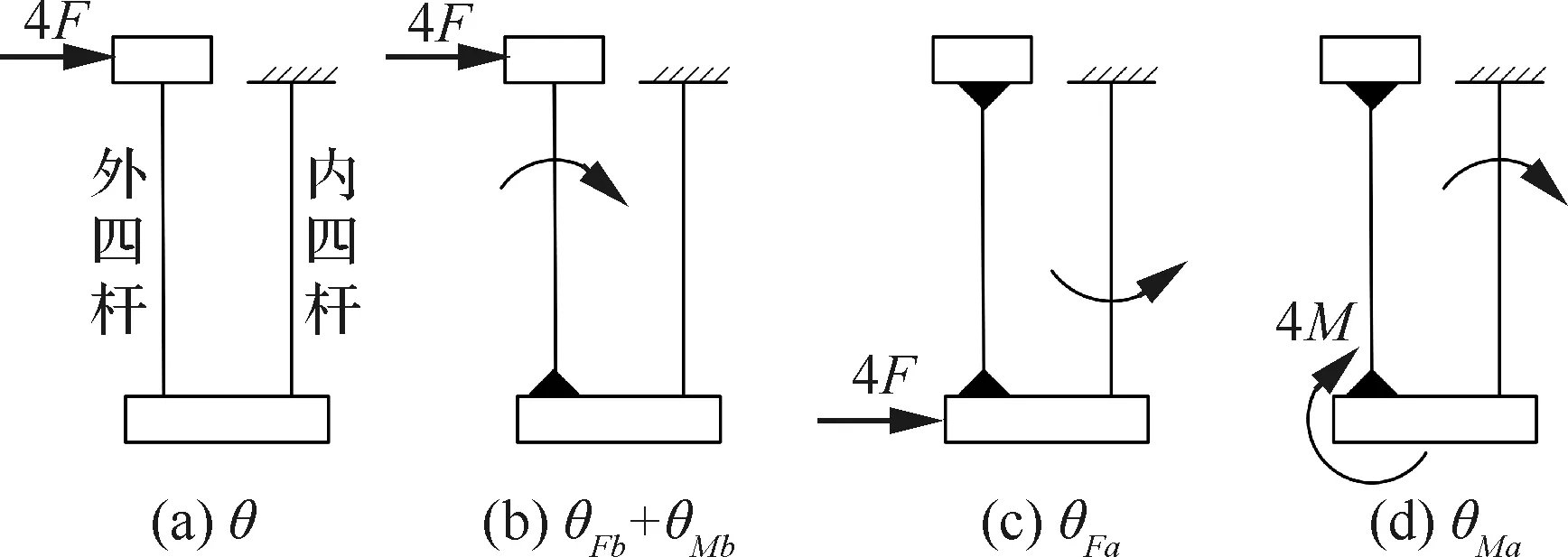
图10 PPR柔性运动副伴生转角示意图Fig.10 Schematic diagrams of parasitic rotation principle of PPR compliant joint

2.2.2 微定位平台伴生转角

5-PPPR柔性微定位平台支链的对称结构，虽消除了动平台沿方向运动时的伴生转动，但、方向运动时伴生转角依旧存在。以方向为例，对平台施加驱动位移，动平台产生伴生转角为方向支链绕轴方向的偏转角，如图11(a)所示，包括被动副受力偏转及驱动副受力矩发生偏转及扭转等共同影响。支链被动副绕轴方向偏转角由于对称结构相互抵消，如图11(b)所示，仅存在驱动副偏转角。

基于内力分析，方向支链被动副所受作用力及驱动副所受力矩分别为

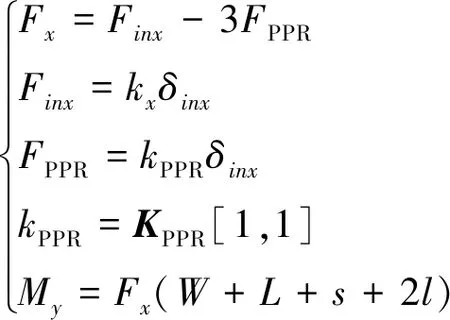
(38)

式中:、和、分别表示平台和PPR运动副的反作用力及其平移刚度。

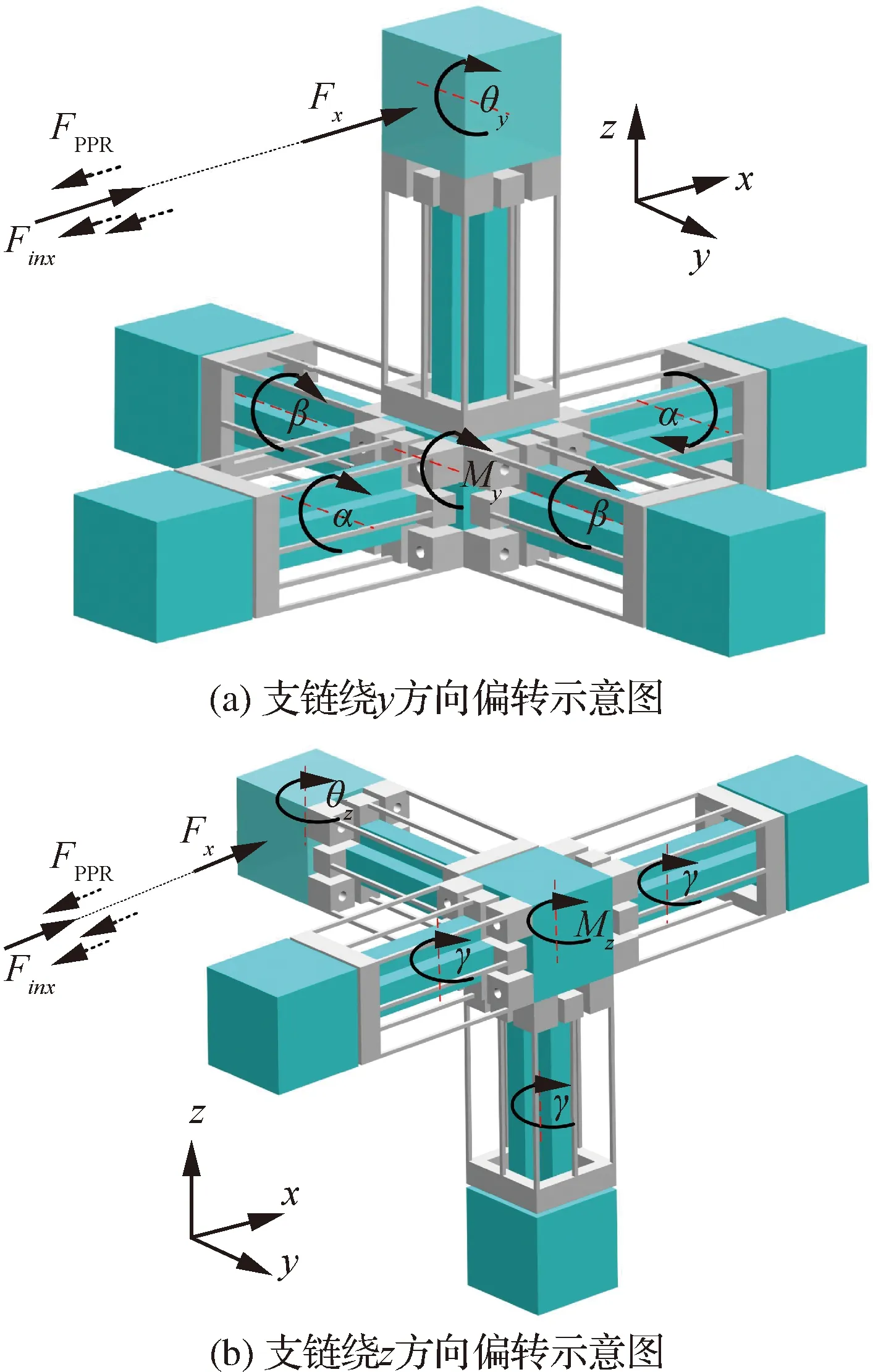
图11 支链伴生转动示意图Fig.11 Schematic diagrams of parasitic rotation of limbs

基于2.2.1节理论模型，其伴生转角与输入力成一次线性关系，因此该支链被动副受作用力产生的伴生转角可表示为

(39)

对于支链驱动副，沿轴方向两运动副发生偏转，其偏转角为，沿轴方向两运动副发生扭转，扭转角为，如图11(a)所示，则有：

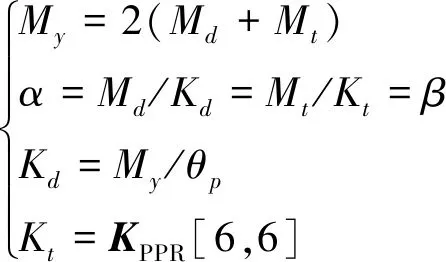
(40)

式中：、分别为支链驱动副偏转、扭转力矩；、分别为运动副的偏转、扭转刚度。

基于式(40)，支链驱动副偏转角为

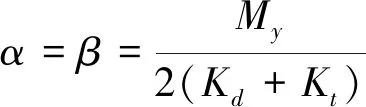
(41)

同理求得图11(b)中驱动副偏转角。故柔性微定位平台方向单轴驱动时，输出动平台所产生绕轴伴生转角为

=+

(42)

同理，方向单轴驱动产生的伴生转角为

=

(43)

根据几何关系，当平台、方向双轴同时驱动时，其产生的伴生转角的最大值为

(44)

2.3 考虑伴生转动的平台输出位移分析

平台输入、输出位移之间的关系决定其定位精度，伴生转动、丢失运动等是影响平台输出位移的主要因素，需分别进行探究。

2.3.1轴方向输出位移

平台方向施加驱动位移，因其无伴生转动现象，其输出位移仅与该支链被动副丢失运动有关。运动副内四杆结构～受拉力，外四杆结构～受压力，其所受力为为

=(-4)4

(45)

基于线弹性梁变形理论，中间刚性平台及刚性连接件Ⅱ的受力弯曲形变量为

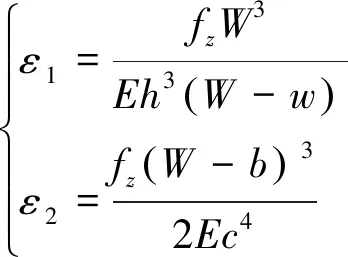
(46)

式中：、、、为运动副结构参数，见图5。

刚性连接件Ⅰ及十字杆压缩变形量为

(47)

内侧柔性杆的伸长及外侧柔性杆压缩均导致丢失运动，其总形变量为

(48)

故平台方向的总运动丢失量为

=++++

(49)

因此，动平台方向输出位移为

=-

(50)

2.3.2、轴方向输出位移

方向施加驱动位移时，输出位移受丢失运动及伴生转动共同影响，综合式(46)～式(49)，鉴于运动副丢失运动与轴向力的线性关系，平台在该方向的运动丢失量为

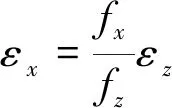
(51)

式中：为每根柔性杆所受轴向力，其表达式为

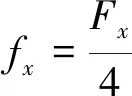
(52)

受伴生转动影响，支链被动副在该情况下形变简化示意图见图12，两支链对称偏转，并产生向偏转位移。动平台连接处由于对称结构无偏转角产生，偏转部件长度为运动副中反向串联柔性杆的等效长度2，根据几何关系：

=2sin2≈

(53)

因此，动平台在方向输出位移为

=-+

(54)

同理，可以分析平台方向输出位移。

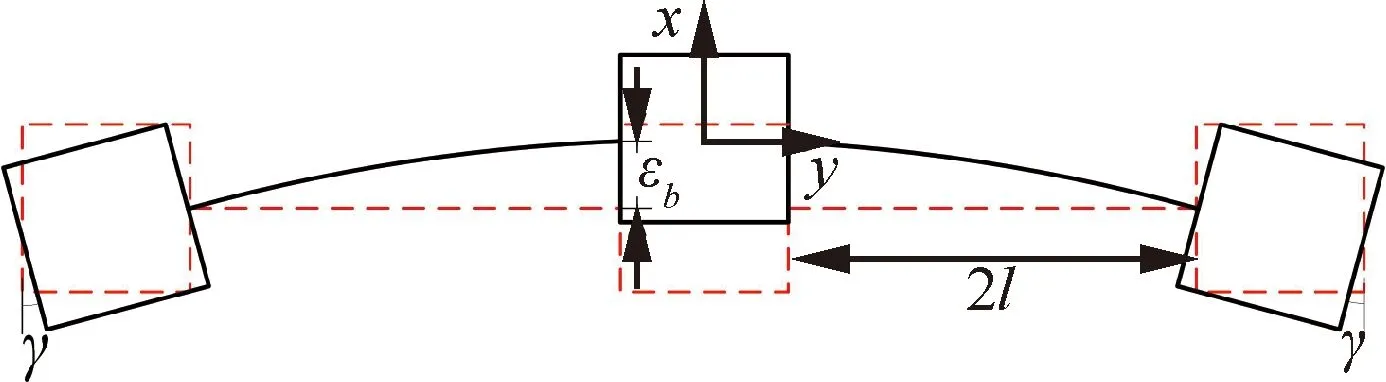
图12 偏转位移Fig.12 Deflection displacement

2.4 模态分析

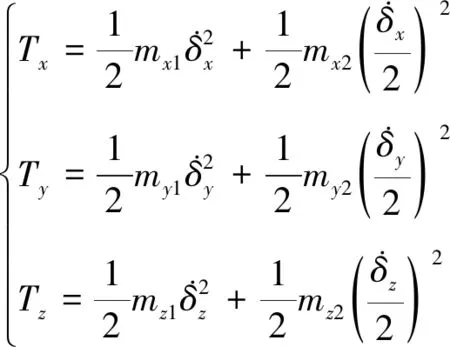
(55)

考虑到平台各部件运动状态不完全一致，式中2、2、2分别为运动副中间平台及内四杆结构的等效质量，1、1、1为其余部件在各方向等效质量，各部分等效质量为

(56)

式中：～为图5(a)中运动副各部件质量。

因此，平台的总运动动能为

=++

(57)

平台的总运动势能为

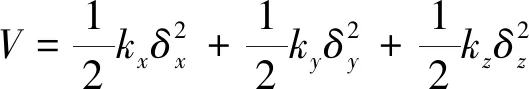
(58)

将式(58)代入拉格朗日方程：

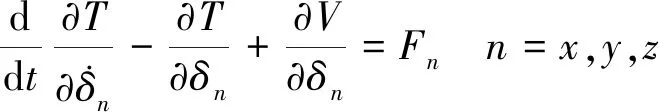
(59)

根据特征方程，微定位平台的固有频率为

=,,

(60)

3 仿真验证

为验证平台静动态特性理论模型正确性，采用ABAQUS对其进行有限元仿真，平台材料选用AL-7075，其弹性模量71.7 GPa，剪切模量为26.9 GPa，屈服强度为503 MPa，密度为2 810 kg/m，运动副尺寸参数如表1所示。

表1 PPR柔性运动副的尺寸参数Table 1 Dimension parameters of PPR compliant joint.

3.1 刚 度

如图13所示，分别沿平台轴、轴方向施加0～1 mm的驱动位移，驱动点反作用力的理论值与仿真值曲线如图14所示。

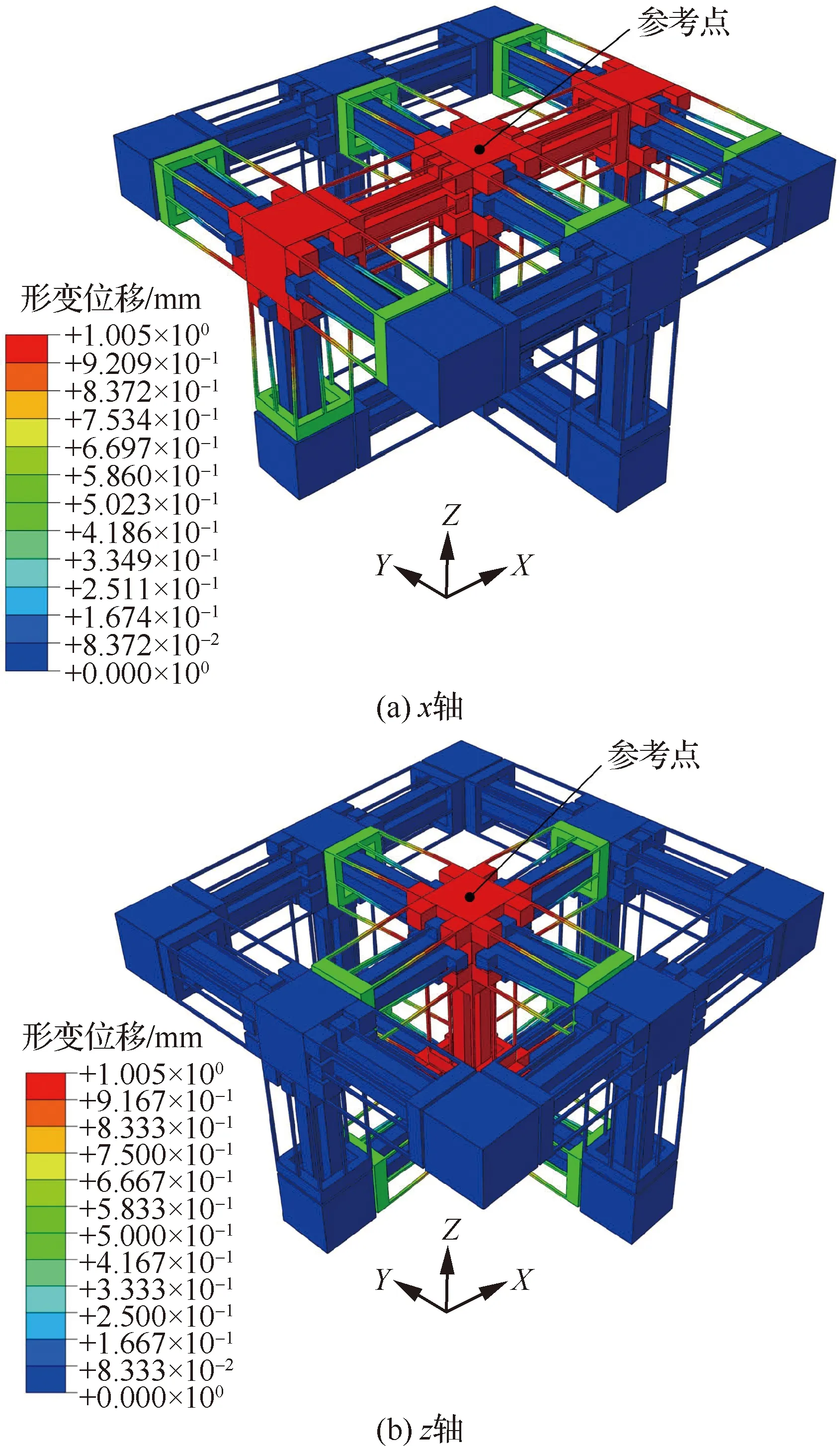
图13 柔性微定位平台有限元仿真Fig.13 Finite element analysis of stage

如图14所示，0～1 mm驱动范围内，轴方向反作用力的理论及仿真最大值分别为19.70 N、19.40 N，其理论与仿真值之间的最大相对误差不超过1.52%；轴方向反作用力的理论及仿真最大值分别为17.74 N、17.35 N，最大相对误差不超过2.20%；上述理论与仿真结果的高度吻合也验证了平台刚度理论模型的正确性。

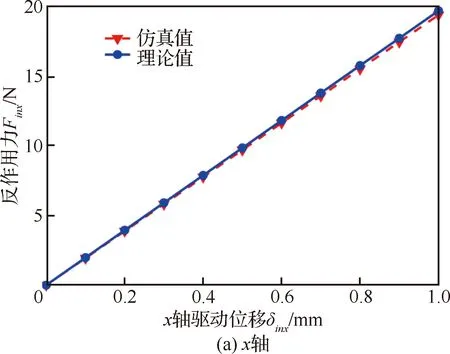
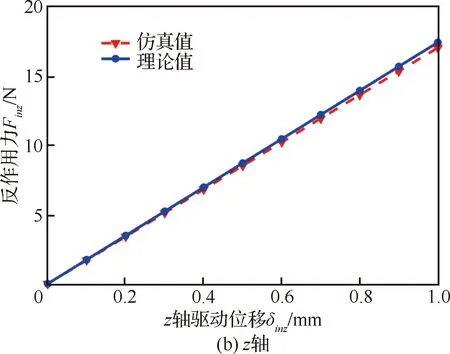
图14 柔性微定位平台驱动点反作用力Fig.14 Reaction forces of the driving point of the stage

基于仿真结果，两种运动状态下，结构中最大应力分别为99.85、99.91 MPa，均小于材料许用应力；微定位平台刚度在0～1 mm驱动范围内呈现严格的线性变化趋势，也体现出运动副反向串联结构避免应力刚化效应的有效性及平台良好的线性特性，有助于提高平台稳定性及抗震性能。

3.2 伴生转角

微定位平台在单轴驱动和多轴驱动时具有不同的伴生转动效果。本文仅考虑单轴驱动及、双轴驱动两种驱动状态，其伴生转角、与驱动位移关系的理论、仿真结果如图15所示，由图可知：

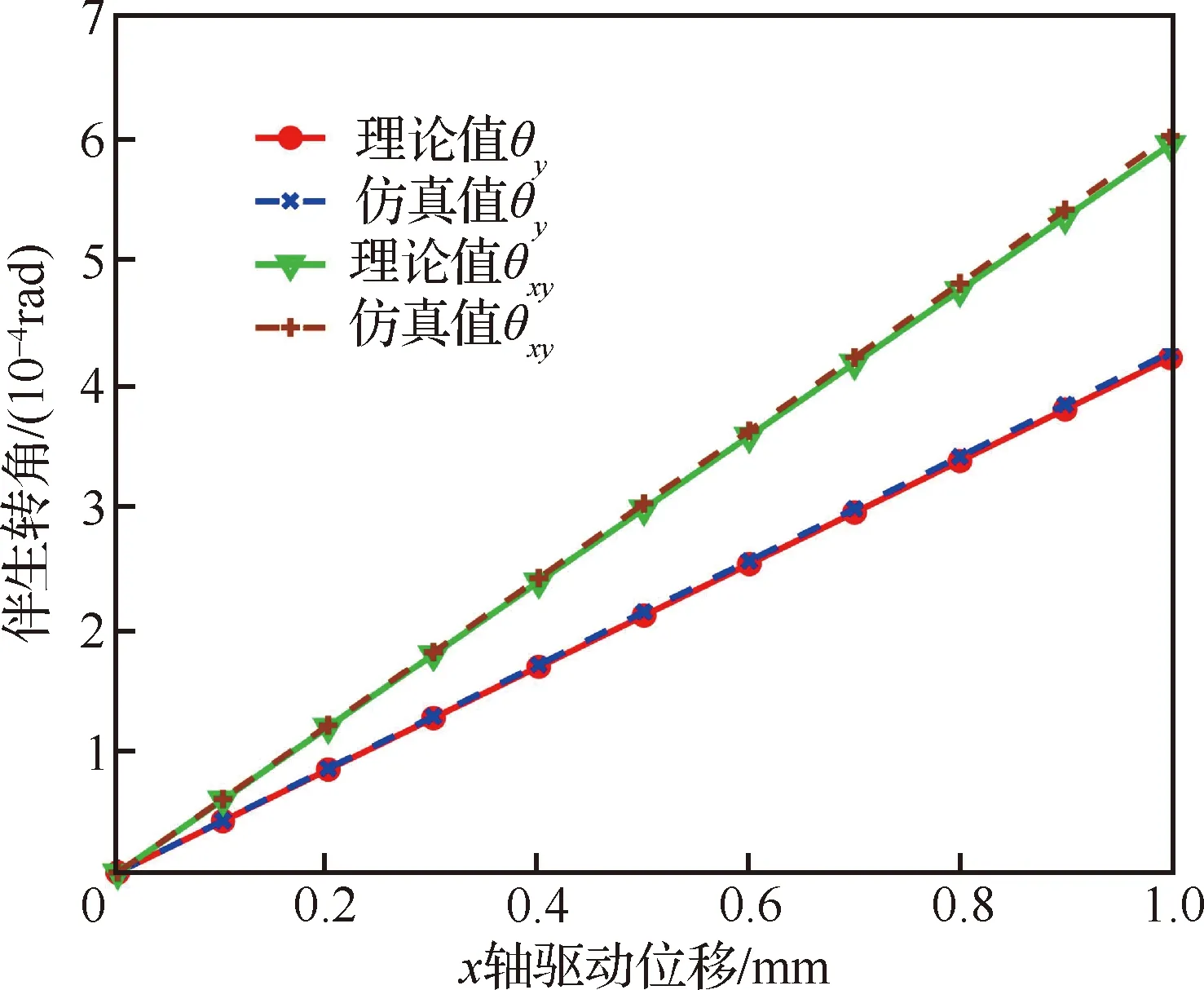
图15 柔性微定位平台伴生转角Fig.15 Parasitic rotational angles of stage

1) 对于给定0～1 mm驱动位移，单轴驱动最大伴生转角理论、仿真值分别为4.21×10rad 和4.26×10rad；双轴驱动最大伴生转角分别为5.95×10rad和6.02×10rad，最大相对误差分别为1.19%和1.23%，验证了理论模型的正确性。

2) 双轴驱动伴生转角仿真结果为单轴驱动的1.41倍，这与式(44)理论结果基本吻合。

3) 两种运动状态下，动平台的伴生转角与驱动位移呈线性关系，这与文中伴生转动理论模型相一致，也进一步验证平台良好的线性特性。

3.3 输出位移

图16(a)所示为平台轴方向丢失运动的理论与仿真值曲线，在驱动位移0～1 mm范围内的理论与仿真值最大值分别为2.88 μm和3.04 μm，最大相对误差不超过5.56%，运动丢失率不高于0.31%。平台轴方向输出位移与丢失运动及伴生转动引起的偏转位移均有关，图16(b)所示为两者综合作用引起的输入、输出位移差的理论与仿真值曲线：

1) 在不考虑伴生转动的条件下，平台的理论值与仿真值呈相反变化趋势，最大相对误差达585%。

图16 柔性微定位平台的输入输出位移关系Fig.16 Input-output displacement relation of the stage

2) 考虑平台伴生转动引起的偏转位移，其理论与仿真值之间最大相对误差降低至原来的5.37%，理论模型精度显著提高，说明了大行程微定位平台考虑伴生转动影响的有效性及必要性，也进一步验证了理论模型的正确性。

3) 仿真结果表明平台方向输入、输出位移差最大值仅为0.86 μm，说明该平台在毫米级运动范围内依旧保持亚微米级的高定位精度。

3.4 耦合位移

平台不同输入点之间相互干扰造成的位移称为平台的输入耦合，动平台在非输入方向上的位移称为平台的输出耦合，二者分别对应平台的驱动解耦及运动解耦特性。

图17(a)所示为轴驱动时，、轴输入点输入耦合位移。仿真结果表明：平台、方向驱动点输入耦合位移分别为1.12×10mm、1.82×10mm，均小于驱动位移的0.02%。

图17 柔性微定位平台的输入输出耦合Fig.17 Input and output couplings of the stage

图17(b)所示为轴驱动时，动平台、方向输出耦合位移。仿真结果表明：动平台中心点各方向输出耦合位移分别为7.86×10mm、3.94×10mm，均小于驱动位移的0.04%。

轴驱动时，()支链的对称布局使动平台不存在输入及输出耦合，解耦特性良好。

综合以上仿真结果，微定位平台各项静态特性的理论值、仿真值及其相对误差如表2所示；在考虑伴生转动和不考虑伴生转动条件下平台输入、输出位移差如表3所示。

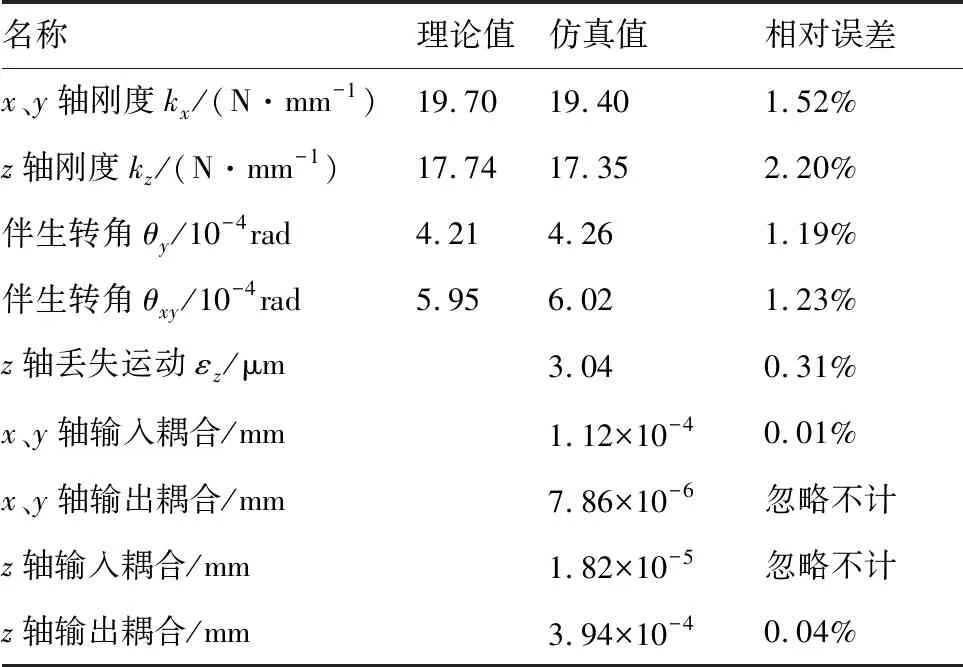
表2 平台静态特性的理论、仿真值及相对误差

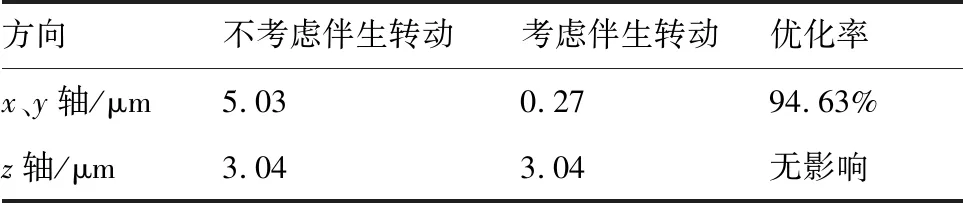
表3 平台输入、输出位移差Table 3 Difference between input-output displacements

3.5 模 态

图18所示为平台的1～6阶模态振型示意图，平台固有频率的理论值、仿真值及相对误差如表4所示。

图18 柔性微定位平台1～6阶模态振型Fig.18 1-6 order mode shapes of stage

表4 平台固有频率的理论、仿真值及相对误差

平台前3阶固有频率理论值与仿真值的相对误差分别为0.96%、0.96%和1.98%，具有较高的一致性；此外，平台1～3阶固有频率与4～6阶固有频率的显著差异，表明平台在非自由度方向具有良好的抗干扰能力，抗震性能优越。

综合理论及仿真分析结果，该定位平台具有行程大、解耦性好、定位精度高、稳定性强、抗震性能好等优点，可用于卫星精密光学器件的姿态调整及机器人在轨精细操作的末端执行器。

4 灵敏度分析和参数优化

4.1 灵敏度分析

为设计满足性能需求的微定位平台，需进一步探究柔性部件结构参数对平台静、动态特性的影响关系。主要包括柔性杆的长度、厚度、杆间距与平台的前3阶固有频率、，方向运动产生的伴生转角及轴方向丢失运动之间的灵敏度关系，进而为微定位平台的结构设计及优化提供理论依据，其分析结果如图19所示。

上述柔性杆结构参数灵敏度分析结果表明，在相同输入位移条件下：

1) 平台前三阶固有频率、随杆长度、杆间距增大而减小，随杆厚度的增大而增大。

2) 平台轴方向丢失运动随杆长度的增大而减小，随杆间距、杆厚度的增大而增大。

3) 平台轴方向的伴生转角随杆长度、杆间距的增大而减小，随杆厚度的增大而增大。

比较图19(a)～图19(d)发现，杆厚度对、以及的影响较大，杆间距次之，杆长度影响最小；对于丢失运动，杆厚度对其影响灵敏度最大，杆长度次之，杆间距影响灵敏度最小。

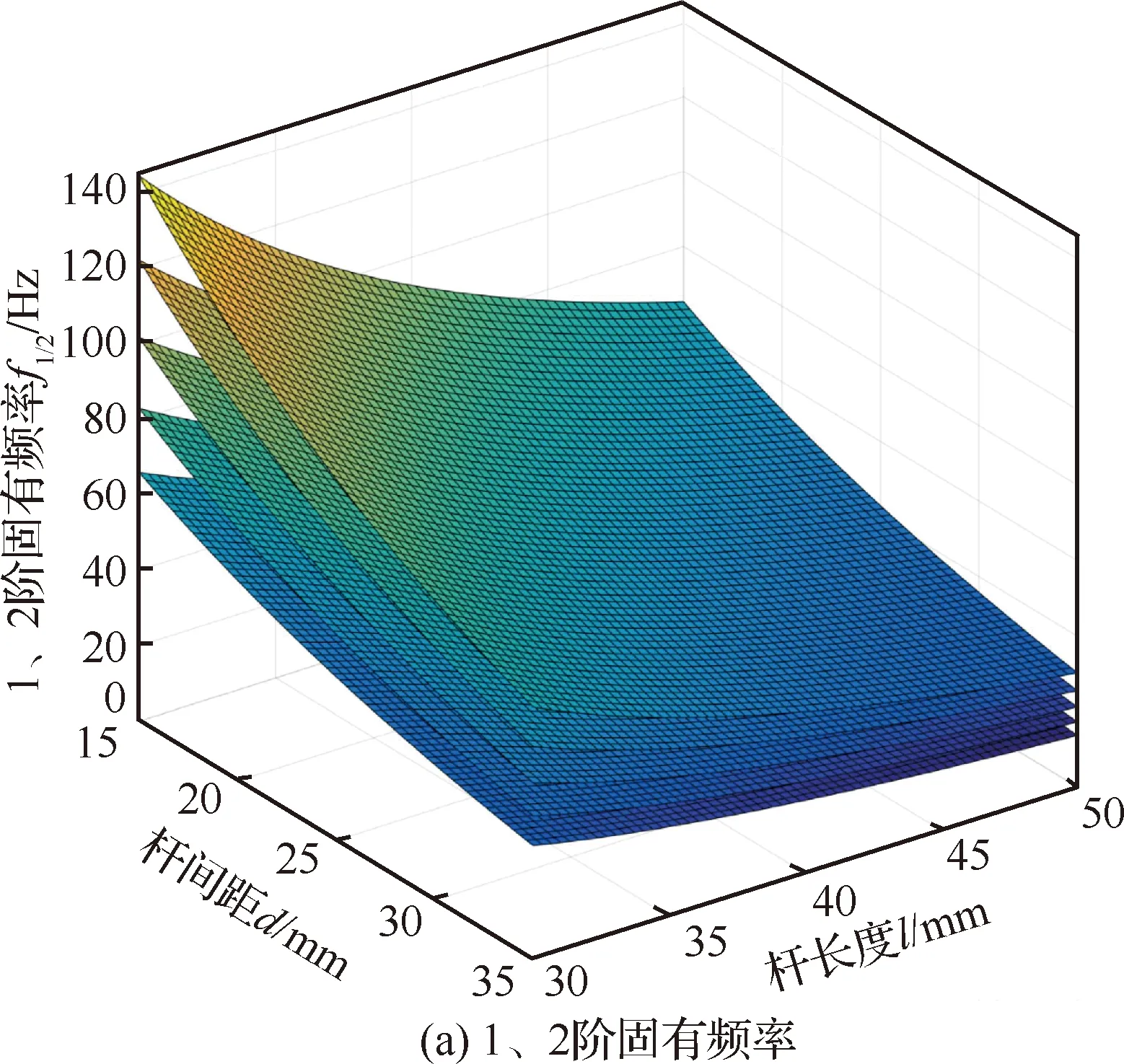
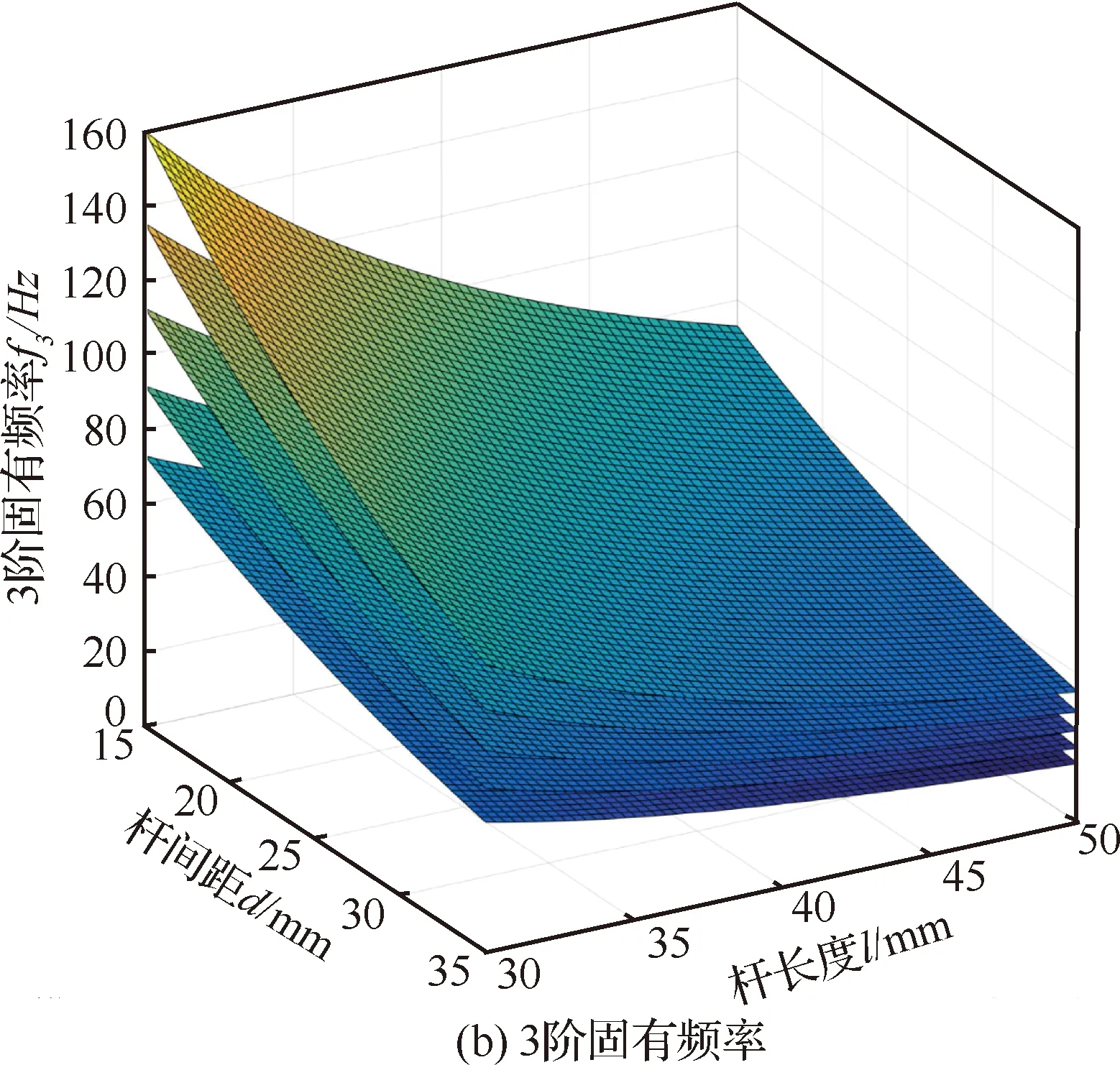
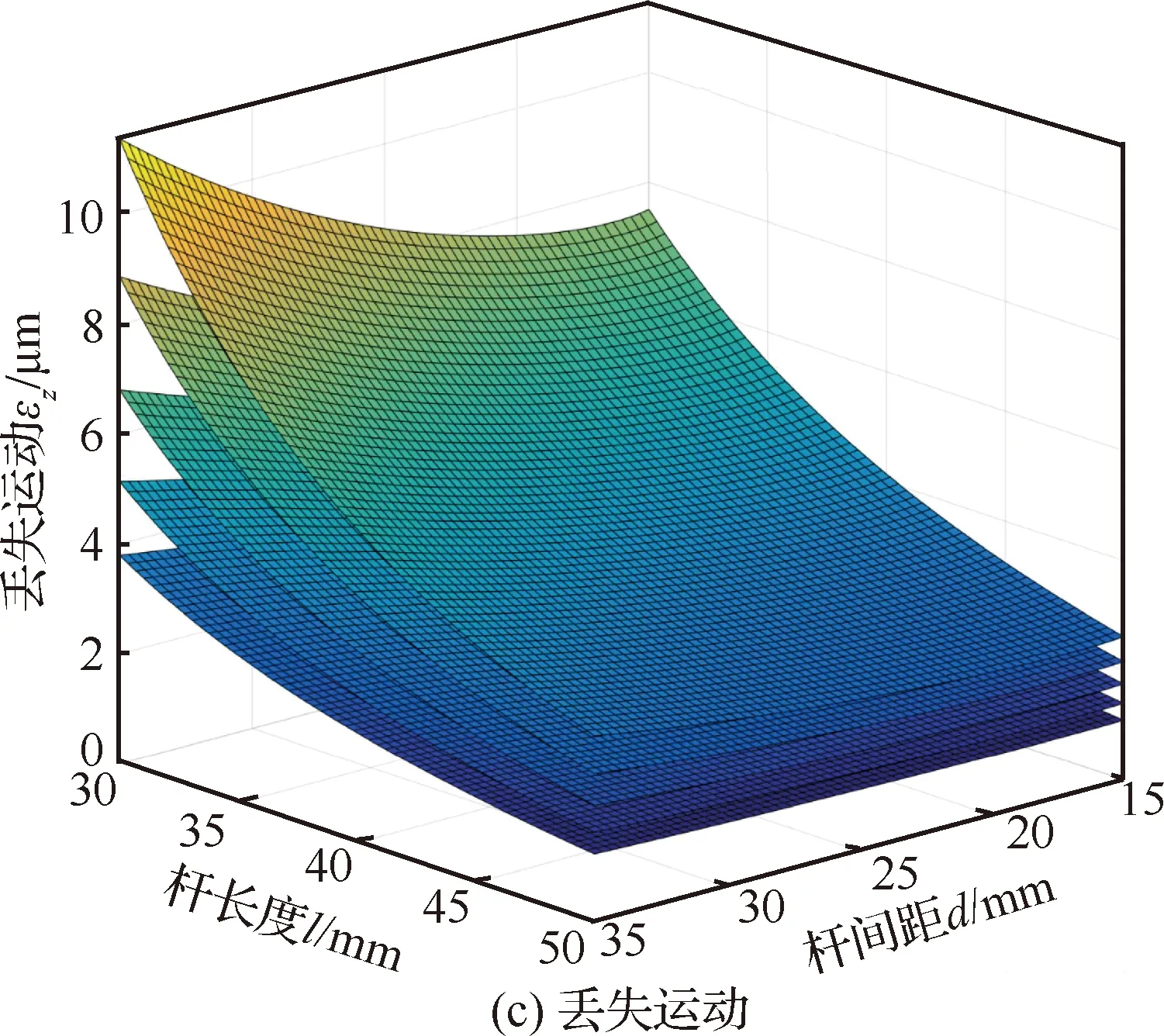
图19 柔性杆结构参数对平台静动态特性的灵敏度分析Fig.19 Sensitivity analysis of parameters of compliant beams

4.2 参数优化

上述灵敏度分析仅限于柔性结构单参数对平台特性的影响，并未考虑参数间耦合，有必要建立其全局优化模型，并开展优化研究。

微定位平台柔性部件的主要结构参数有柔性杆长度、厚度及杆间距。基于灵敏度分析，取其优化模型的设计变量及上下限值为

(61)

以保证平台运动精度为首要优化目标，即使其伴生转角及丢失运动最小化，同时具有较大的固有频率，其优化模型的目标函数表示为

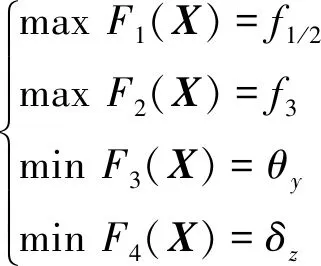
(62)

同时，应满足以下约束条件：

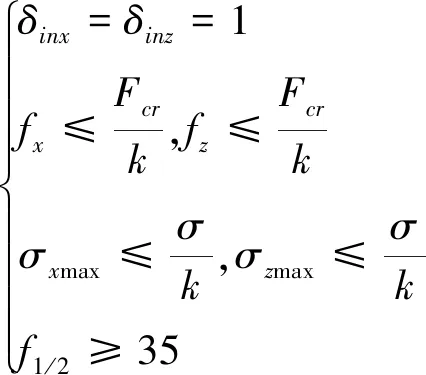
(63)

式中：取安全系数=2。

基于MATLAB中的fmincon和fgoalattain函数，开展微定位平台多目标参数优化研究，平台优化前、后的结构及性能参数如表5所示。优化结果表明：相同输入条件下，优化后平台的伴生转角和丢失运动分别降低了28.9%和21.5%，进一步提高了平台的运动精度及综合性能。

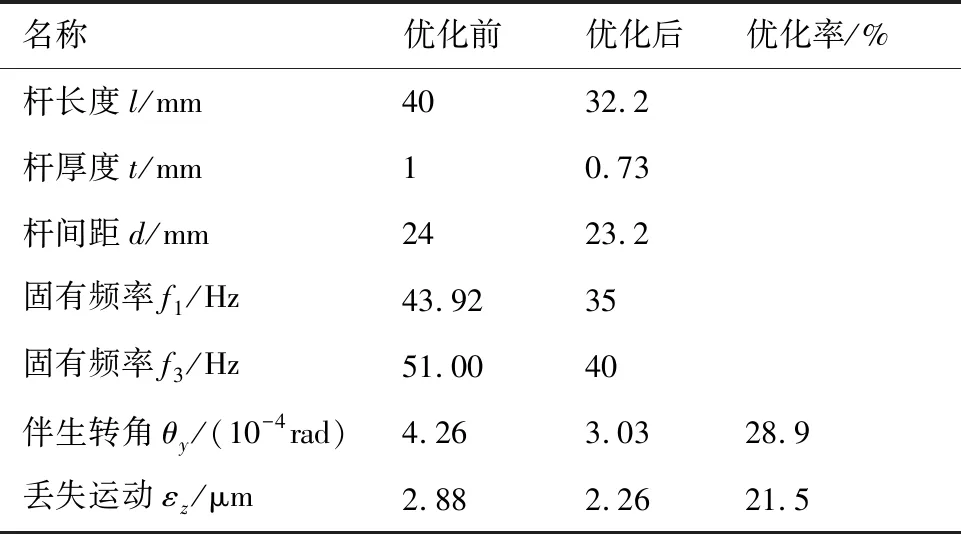
表5 平台结构及性能参数Table 5 Structure and performance parameters for stage

5 结 论

1) 提出了一种PPR型大行程柔性运动副，并基于该运动副设计了一种新型5-PPPR型大行程柔性微定位平台。

2) 提出了对大行程柔性运动副及微定位平台伴生转角的理论建模方法，并在考虑伴生转动情况下，将输出位移的理论误差降低了94.63%，极大的提高了理论模型精度。

3) 通过有限元仿真验证了理论模型的正确性，并对平台耦合位移进行分析。结果表明：输入、输出耦合分别小于驱动位移的0.02%和0.04%，平台运动完全解耦。

4) 对平台柔性部件进行了灵敏度分析及参数优化，相同驱动条件下伴生转角及丢失运动分别降低了28.8%和21.5%，进一步提升了平台的定位精度及综合运动性能。

微定位平台的动力学分析及控制，实验系统的搭建及相关实验测试，将在后续工作中做进一步研究与完善。