6/4极无轴承开关磁阻电机悬浮控制原理与实现
2022-09-05缪伟曹鑫刘晨昊邓智泉
缪伟,曹鑫,*,刘晨昊,邓智泉
1. 南京航空航天大学 自动化学院,南京 211106 2. 杭州海康机器人技术有限公司,杭州 310052
开关磁阻电机(Switched Reluctance Motor, SRM)定、转子均为凸极结构,仅定子齿极上安装有绕组,因此具有结构简单坚固、可靠性高、成本低、容错性好等优点,在高速电机研究领域受到了广泛关注。由于转子上既无绕组又无永磁体,因此尤其适合于恶劣工况下运行,在航空航天等领域多有应用。另外,为提高电机转速以进一步提升航空航天领域电驱系统的功率密度,目前可通过采用磁轴承技术对电机转轴进行主动悬浮控制,实现高速转轴的无摩擦、无润滑运行,从而解决高速电机中轴承磨损及发热严重的问题。为进一步提高系统集成度及转子临界转速,在电机定子齿极上增加一套绕组取代磁轴承定子绕组,通过控制绕组电流实现转子主动悬浮,由此形成了无轴承电机技术。
将无轴承技术应用于开关磁阻电机领域,由此得到无轴承开关磁阻电机(Bearingless Switched Reluctance Motor, BSRM)。最先研究的BSRM为双绕组结构,即每一个定子齿极上均有2套绕组,其中一套绕组的电流主要控制电机转矩,而调节另一套绕组电流可实现转子悬浮。随着系统集成度进一步提高,单绕组无轴承开关磁阻电机得到广泛研究。虽然单绕组BSRM绕组数目减少一半,但悬浮和转矩控制的耦合度增加,控制算法较为复杂。目前,学者们主要针对12/8极、8/6极、8/10极、12/14极BSRM进行研究。
BSRM悬浮控制的本质在于在径向相对位置构造不平衡且可控的气隙磁密分布,双绕组与单绕组采用不同的手段实现该目标。12/8极是BSRM领域研究最广泛、最深入的一种结构,针对12/8极BSRM提出的传统电流控制方法,采用三相轮流导通的模式,通过构造每相正交分布的4个齿极处两两径向相对位置的不对称气隙磁密实现转子的稳定悬浮。双绕组结构采用主磁通叠加偏置磁通的方式,因而绕组可正向、反向串联以减少功率变换器桥臂数目。但为实现单绕组结构相对齿极绕组的不对称励磁,每套绕组电流必须独立控制,所以定子齿极上的12套绕组共需要12个桥臂的不对称半桥功率变换器进行驱动,所需器件较多,系统体积较大。
本文研究的6/4极BSRM与传统12/8极BSRM相比,绕组数目减少,换相频率降低,主电路所需要的不对称半桥电路的桥臂数为12/8极BSRM的一半,电机本体和驱动器结构大为简化。然而,电机本体结构的简化使得转矩和悬浮力在产生机理上存在较强的耦合,这增加了6/4极BSRM的控制难度,以往的BSRM悬浮机理和控制方法不再适用。因此,本文重点分析6/4极BSRM的结构特点及其运行特性,研究其两自由度悬浮控制策略。
首先介绍了6/4极与12/8极BSRM结构和悬浮实现上的区别,详细阐述了6/4极BSRM的控制难点;其后,围绕转矩和径向悬浮力的协调控制方法以及两相悬浮力分配算法,深入分析了本文所提控制策略的原理;最后,基于MATLAB/Simulink和一台6/4极BSRM实验平台,通过仿真和实验验证了原理分析和方法实现的可行性和有效性。
1 6/4极BSRM运行原理
1.1 悬浮原理
单绕组BSRM与普通SRM在结构上具有一定的相似性,每个定子齿极上仅绕有一套集中绕组,但单绕组BSRM的悬浮机理决定了其每套绕组电流必须独立控制以构造相对齿极不平衡气隙磁密,如图1(a)所示。传统12/8极BSRM每一相包含4套在平面内呈正交分布的独立绕组,对同一相绕组相对齿极不对称励磁便可产生不平衡气隙磁密,以A相导通为例,若绕组电流1>3,产生水平向右的径向力1-3;2>4,产生竖直向上的径向力2-4。通过控制相对齿极的绕组电流大小调节、方向径向力的大小和方向。6/4极BSRM绕组数目减少一半,每相仅有2套独立绕组,不对称励磁仅能产生一维径向力,如图1(b),若仅对B相2套绕组励磁,则只能产生方向的悬浮力。因此,对于6/4极BSRM必须双相导通至少3套绕组,才能产生二维平面内任意方向的径向悬浮力。为降低控制复杂度,本文中的6/4极BSRM采用双相共导通4套绕组的模式以实现径向两自由度悬浮,例如AB两相工作时径向悬浮通过同时导通A1、A2、B1、B2 这4个齿极上的绕组实现,将各导通齿极下的电磁力分解到直角坐标系,方向合力为1+1-2-2,方向合力为2-1(方向均指向坐标轴正方向)。因此,与传统12/8极BSRM不同,考虑双相耦合及悬浮力分配是6/4极BSRM悬浮控制的核心。
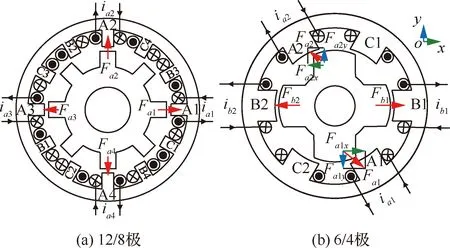
图1 BSRM结构示意图Fig.1 Structure of BSRM
1.2 数学模型
根据6/4极BSRM运行原理的分析,双相导通是转子稳定悬浮的必要条件,因此需研究电机双相导通时的数学模型。基于电机结构和径向悬浮机理的相似性,本文采用文献[22]推导的6/4极BSRM双相导通时的数学模型,以导通A、B两相为例:

(1)
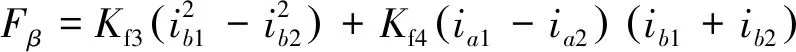
(2)
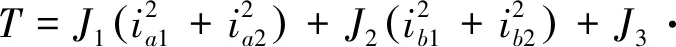
(1-2)(1-2)+12+12
(3)
=cos+sin
(4)
=cos-sin
(5)
式中:、分别为BSRM双相导通时在旋转坐标系下和方向径向力;、为在静止直角坐标系下和方向径向悬浮力;为转矩;1、2、1、2分别为A1、A2、B1、B2绕组电流;~、~为与转子位置角和电机参数相关的系数;如图2所示,为轴与轴的夹角;为轴与轴的夹角。
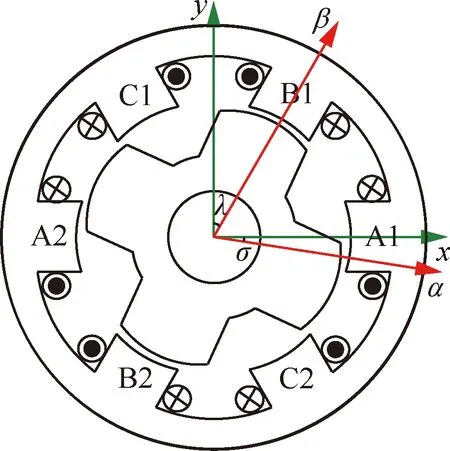
图2 直角坐标系与旋转坐标系Fig.2 Rectangular and rotating coordinate systems
2 6/4极BSRM径向悬浮控制方法
2.1 换相策略
图3为6/4极BSRM的电感曲线及导通区间划分示意图。以A、B两相导通为例,在整个导通区间内A相电感曲线处于上升区,可提供足够的正转矩及悬浮力;而B相电感曲线在导通区间前半部分处于上平顶区,电感为最大值,可提供足够大的悬浮力,但在导通区间后半部分处于下降区,会产生一定的负转矩。6/4极BSRM在90°机械周期内按照AB、CA、BC的相序导通。

图3 6/4极BSRM电感曲线及导通区间划分示意图Fig.3 Inductance profile and conduction order of 6/4 BSRM
2.2 控制原理
通过合理分配两相悬浮力,协调控制两相绕组电流以实现转矩和径向悬浮力的主动控制,是6/4极BSRM的控制目标。由式(1)~式(3)可知,径向悬浮力和转矩的表达式中均含有绕组电流的平方项,且3个方程无法求解4个变量,转矩与径向悬浮力的耦合性较强。因此考虑从单、双绕组BSRM悬浮机理的区别出发,将单绕组BSRM的绕组电流分离为转矩电流m(=1,2)和径向悬浮力电流t(=1,2),以期实现转矩和悬浮力在一定程度上的解耦。为简化控制,和前的系数均取为1,两者之间的数量关系可根据转矩、径向悬浮力的要求通过表达式解算得到。以A、B两相导通为例,两相的绕组电流可表示为
1=+
(6)
2=-
(7)
1=+
(8)
2=-
(9)
将式(6)~式(9)代入式(1)~式(5),可得到新的径向悬浮力和转矩表达式
=+++
(10)
=+++
(11)

(12)
式中:、、为与转子位置角和电机参数相关的系数。
由图3可知,每相导通60°机械角度,但每隔30°机械角度进行一次换相,为确保换相前后持续导通相转矩电流的连续性,导通相的转矩电流均设为,即
==
(13)
悬浮力电流、产生的转矩分量在径向力负载较小时可忽略不计,电机总转矩可以近似写成:
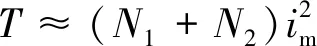
(14)
因此,控制转矩电流即可调节电机转矩。
由式(10)~式(11)可以得到悬浮力电流、的表达式
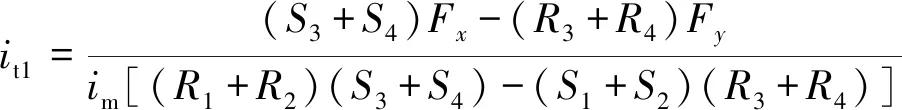
(15)
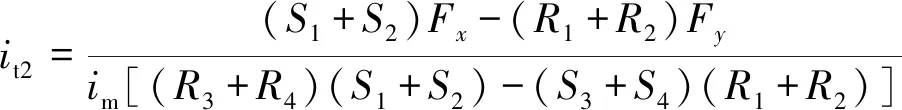
(16)

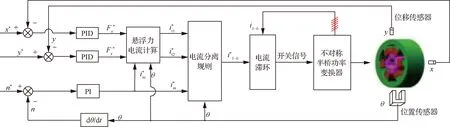
图4 6/4极BSRM控制框图Fig.4 Control block of 6/4 BSRM
3 系统仿真分析
本文首先基于ANSYS Maxwell进行6/4极BSRM电机本体建模,设定绕组激励电流,开环仿真所提算法的电磁特性。然后基于MATLAB/Simulink软件环境进行系统建模与闭环仿真,以期验证本文所提控制算法的性能。因为本课题组现仅有一台6/4极锥形BSRM实验样机,除定、转子形状为特殊的锥形以外,其绕组排布、径向悬浮机理均与普通6/4极BSRM无异。因此,基于该样机开展了仿真与实验验证。
3.1 电磁特性仿真
电磁仿真中电机的尺寸参数如表1所示,为验证6/4极BSRM双相导通的必要性,分别仿真了A、B、C三相仅在各自电感上升30°区间内导通,即单相导通,与根据第2.1节换相策略双相导通2种情况下的转矩与悬浮力。
在导通区间内,通过对同一相的2个齿极绕组不对称励磁构造不平衡气隙磁密,从而产生径向悬浮力。例如,当电机机械角度在[-37.5°,-7.5°]内,AB双相导通时,1=1=3 A,2=2=1 A,1=2=0 A;A相单相导通时,1=3 A,2=1 A,1=2=1=2=0 A。单相导通、双相导通下的转矩和悬浮力波形如图5所示。
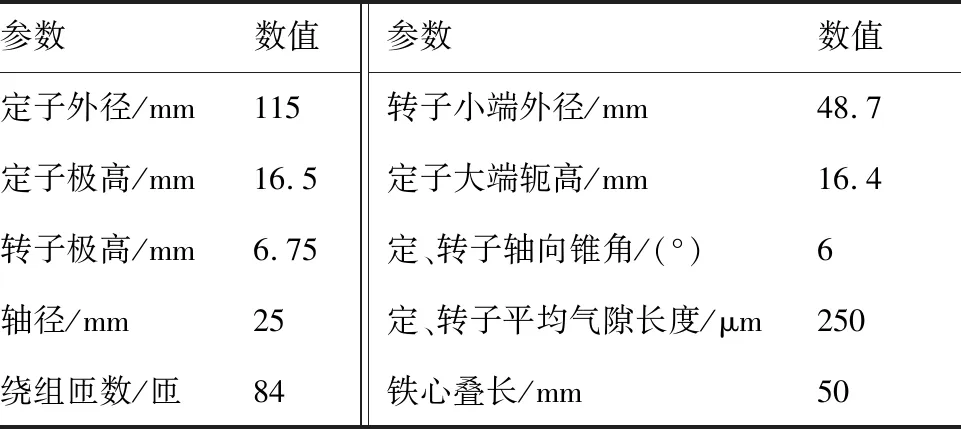
表1 ANSYS Maxwell仿真参数Table 1 Parameters of simulation in ANSYS Maxwell
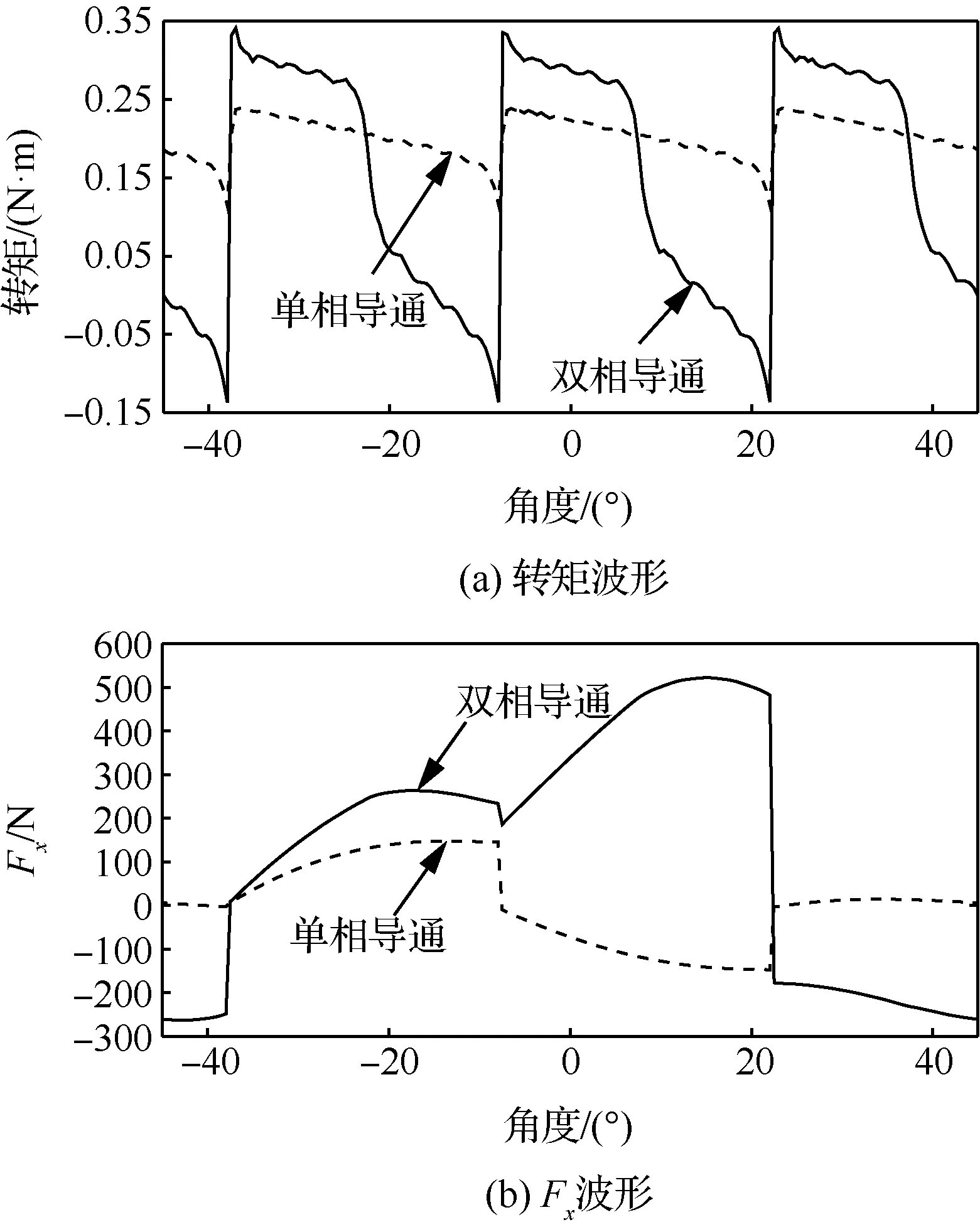
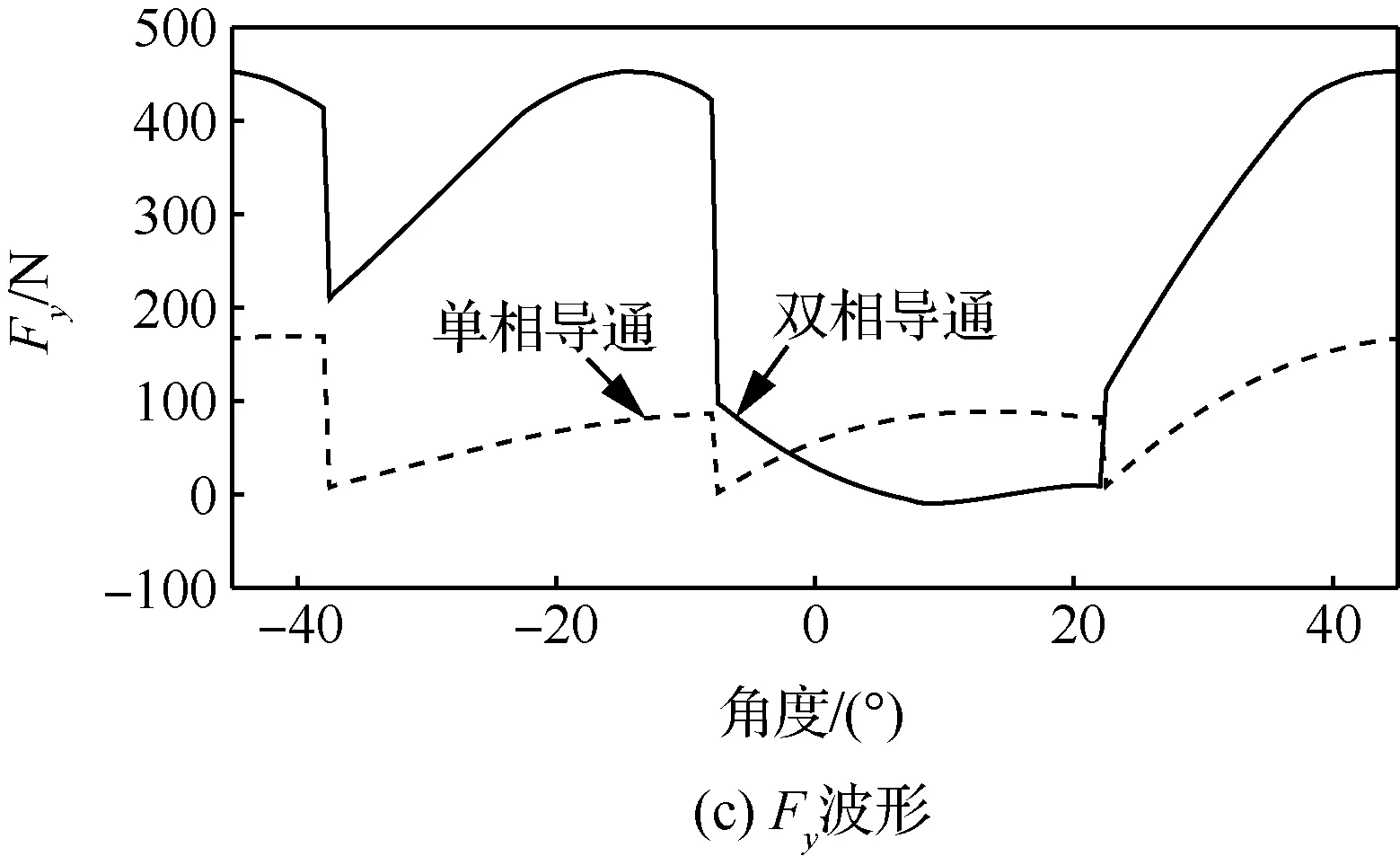
图5 电流大小相等时单相、双相导通的转矩与悬浮力仿真波形Fig.5 Simulation waveforms of torque and levitation forces for single-phase and two-phase conduction with equal currents
单相导通电机转矩最小值为0.11 N·m,不产生负转矩,但产生的径向悬浮力相比于双相导通显著减小。因此,必须采取双相导通模式,以确保任意角度下的、径向悬浮力跟踪。
本文所提控制方法,将绕组电流分解为转矩电流m(=1,2)和径向悬浮力电流t(=1,2)。其中,转矩电流决定系统转矩输出能力,径向悬浮力电流调节、方向的悬浮力大小。图6为相同悬浮力电流,不同转矩电流下的转矩仿真波形,转矩峰值、平均值随转矩电流的增大而增大。
类似地,当控制转矩电流不变,调节悬浮力电流由小到大,产生的径向悬浮力波形如图7所示。随着悬浮力电流的增大,电机、这2个方向的径向出力均显著增加。

图6 相同悬浮力电流、不同转矩电流下的转矩仿真波形Fig.6 Simulation waveforms of torque with the same levitation-force current and different torque currents

图7 相同转矩电流、不同悬浮力电流下的悬浮力仿真波形Fig.7 Simulation waveforms of levitation forces with the same torque current and different levitation-force currents
3.2 控制算法仿真
为验证算法闭环动态及稳态性能,分别进行给定转速2 000 r/min和给定转速从3 000 r/min突变到3 500 r/min这2种情况下的仿真,控制算法仿真参数如表2所示。

表2 控制算法仿真参数Table 2 Parameters of simulation of proposed method
6/4极BSRM采用双相导通模式,导通区间为定、转子齿刚重合位置到定、转子齿对齐位置,即-37.5°~-7.5°。当给定转速为2 000 r/min时,BSRM转速、机械角度转矩波形如图8所示。电机转速经过1 s的调节迅速、准确跟踪给定值。开关磁阻电机定、转子凸极结构导致其转矩存在一定的脉动,根据图3导通区间的划分,电感曲线处于下降区的导通相不可避免地产生负转矩,2 000 r/min 时电机的平均转矩为0.289 4 N·m。
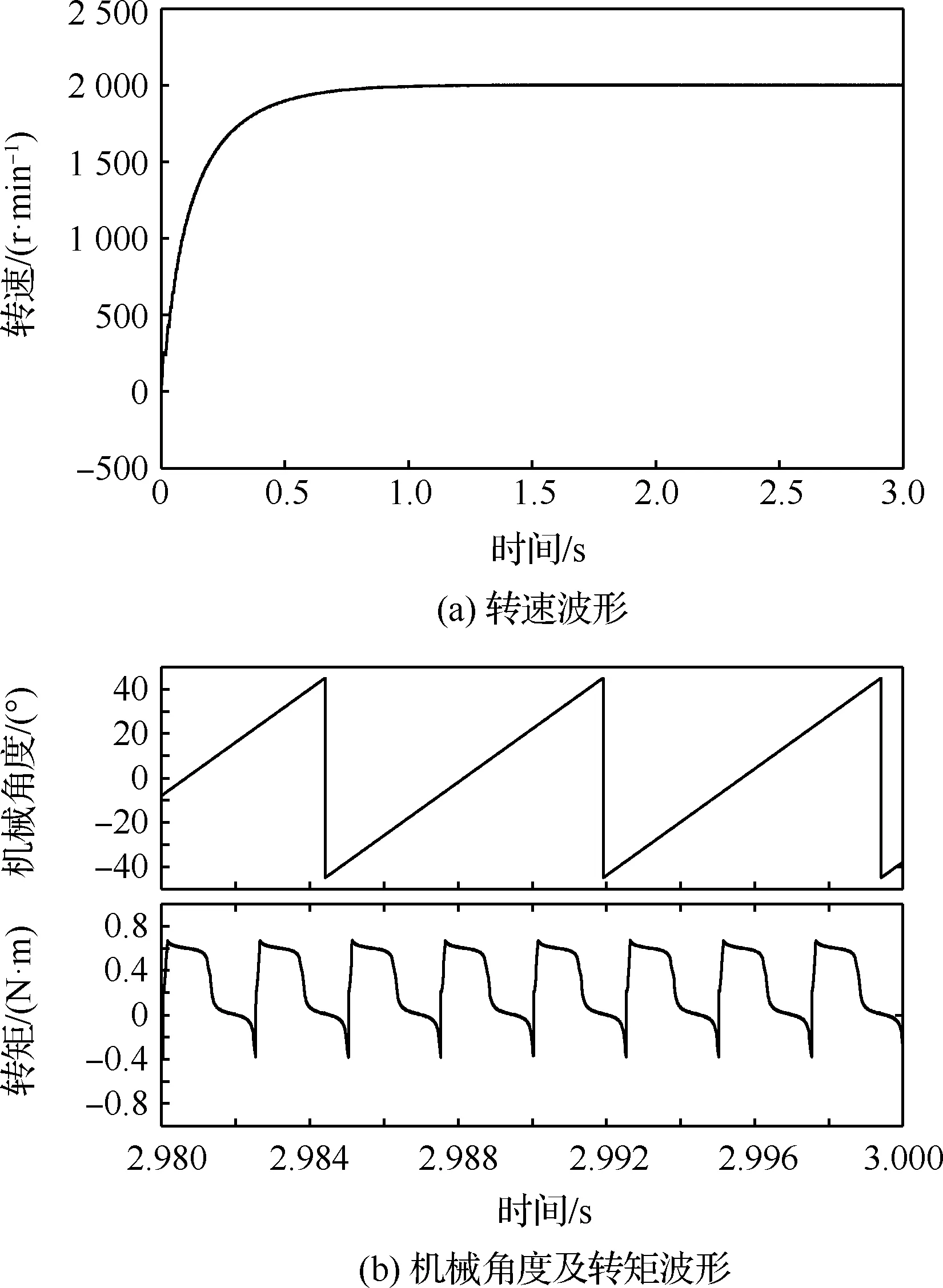
图8 转速2 000 r/min 6/4极BSRM转速机械角度及转矩仿真波形Fig.8 Simulation waveforms of speed and torque of the 6/4 BSRM at 2 000 r/min
给定径向悬浮力,观测实际径向力能否准确跟踪给定值,模拟径向位移闭环仿真。图9为2 000 r/min 时径向和方向悬浮力的波形图,径向悬浮力能准确跟踪给定值,但在换相时刻出现周期性尖峰。原因在于,控制算法设计基于分段推导得到的数学模型,且如图3所示,由于BSRM电感特性,换相时刻对应的三相电感值不同,导致由式(15)、式(16)解算得到的悬浮力电流大小不同,而绕组电流却不能突变以迅速跟踪给定值。

图9 转速2 000 r/min 6/4极BSRM径向悬浮力仿真波形Fig.9 Simulation waveforms of radial levitation forces of the 6/4 BSRM at 2 000 r/min
控制绕组电流大小是6/4极BSRM转矩和径向悬浮力控制的核心,图10为2 000 r/min时的绕组电流仿真波形,其中图10(a)为A相2个绕组A1、A2电流,图10(b)为三相A1、B1、C1电流波形。可以发现,同一相相对齿极的电流波形对称分布,对称中心的电流值为转矩电流大小,在此基础上加、减悬浮力电流得到相对齿极2个绕组电流;三相电流波形可验证电机实际运行时按照算法设定的AB、CA、BC的相序轮流导通。
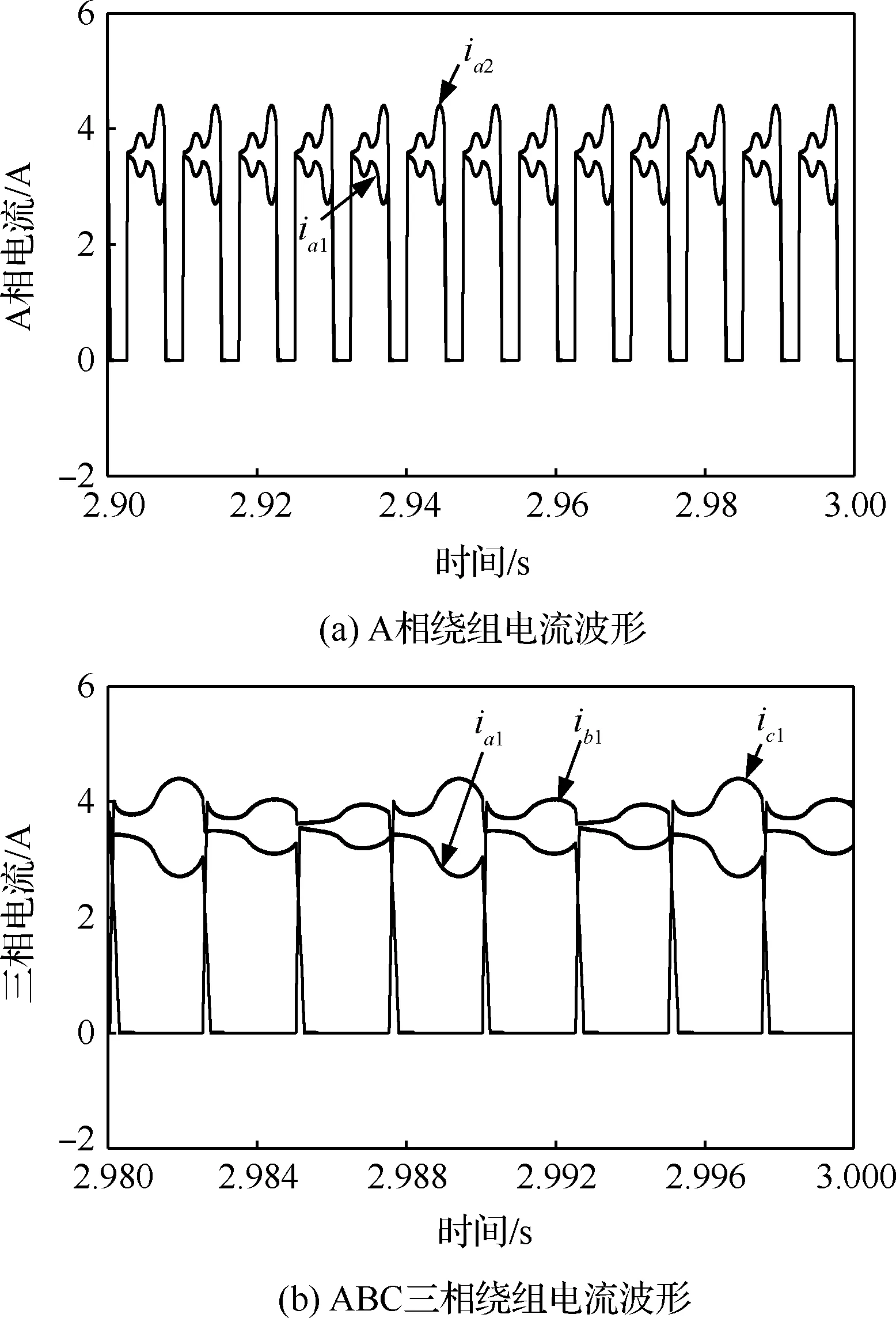
图10 转速2 000 r/min 6/4极BSRM绕组电流仿真波形Fig.10 Simulation waveforms of winding currents of 6/4 BSRM at 2 000 r/min
容错性能是航空航天领域电驱系统的重要评价指标,因此本文对发生单个齿极绕组断路、一相2套绕组均断路2种故障前后算法的控制性能进行了初步仿真验证。图11为电机转速2 000 r/min 时A1齿极绕组发生断路故障前后的转速、径向悬浮力及A相电流仿真波形。由于开关磁阻电机具有强容错性,2 s故障发生后,转速跌落至1 940 r/min,通过转速闭环的调节,非故障齿极绕组电流增加,因此转速又迅速上升,约4.5 s时重新到达给定值2 000 r/min,转速脉动较正常运行状态增加约0.325%。但是由于A1绕组电流为0 A,无法实时跟踪径向力电流,因此导致A相导通区间内悬浮力失控。若要实现故障后的悬浮力跟踪,需设计相应的容错控制算法,在双相导通共3套绕组的情况下重新计算悬浮力分配。
图12为A相2套绕组均发生断路故障时的仿真波形。同样,依赖于开关磁阻电机固有的容错性能,电机仍能正常输出转矩,在转速闭环的调节作用下实现转速控制。但此时仅在BC两相导通时能实现悬浮力的准确跟踪,其他状态下单相导通必定会造成某些方向的悬浮力缺失,给6/4极BSRM的控制带来了新的难题。
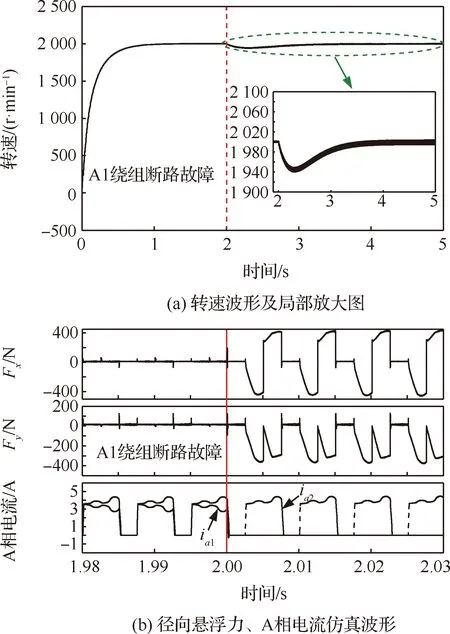
图11 转速2 000 r/min A1绕组断路故障前后6/4极BSRM仿真波形Fig.11 Simulation waveforms of the 6/4 BSRM before and after open circuit fault of A1 winding at 2000 r/min
为验证本文所提算法的动态性,给定转速在3 s时由3 000 r/min突变为3 500 r/min。如图13(a) 所示,当转速给定突变时,实际转速能够快速地跟踪上给定值,图13(b)中转矩的平均值增加,说明此算法调速性能良好。图13(c)~图13(d)为电机绕组电流波形,升速后,由于转矩电流增大,绕组电流均增大。图13(e)~图13(f) 为升速过程的径向悬浮力波形,由于绕组电流增大,电流跟踪的难度增加,径向悬浮力尖峰增大。

图12 转速2 000 r/min A相绕组断路故障前后6/4极BSRM仿真波形Fig.12 Simulation waveforms of 6/4 BSRM before and after open circuit fault of phase A at 2 000 r/min

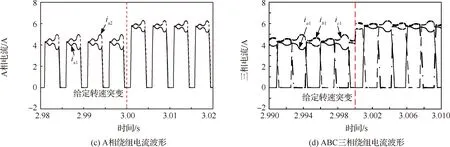
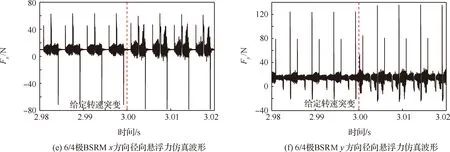
图13 给定转速3 000 r/min突变为3 500 r/min的6/4极BSRM仿真波形Fig.13 Simulation waveforms of 6/4 BSRM with given speed 3 000 r/min suddenly change to 3 500 r/min
4 实验结果及分析
为进一步验证所提算法的正确性,本文在第3节所述的一台6/4极锥形无轴承开关磁阻电机上进行了实验验证,样机和实验平台如图14所示。实验时样机为立式放置,悬浮端采用机械轴承进行辅助限位保护,以防转子未悬浮时的电机“扫膛”。同时,在悬浮端安装了4个电涡流传感器对转轴、方向位移进行检测。非悬浮端采用调心球轴承支撑,另外安装3个光电传感器配合测速齿盘以检测转子的实时转角位置。样机参数与表1仿真参数相同。
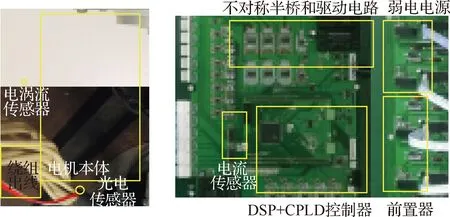
图14 6/4极BSRM样机本体及实验平台Fig.14 Prototype and experimental platform of 6/4 BSRM
图15(a)和图15(b)分别为2 000 r/min和3 000 r/min 稳定悬浮时的位移波形和A相绕组电流波形,图15(c)和图15(d)为其对应的转子轨迹图,2 000 r/min时位移波动约为50 μm,约为辅助轴承游隙的1/4,3 000 r/min时位移波动约为25 μm,约为辅助轴承游隙的1/8,悬浮性能良好。
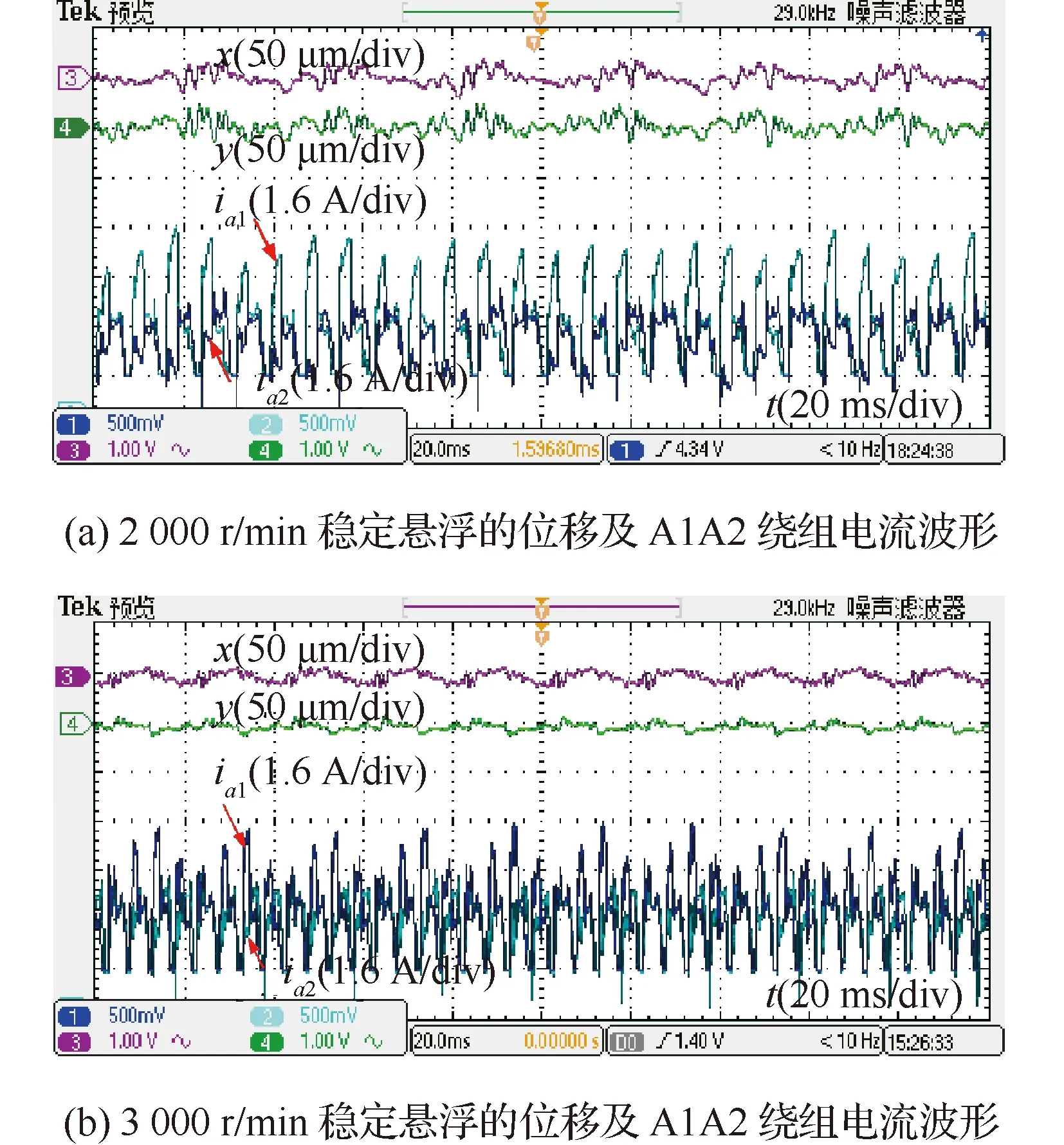
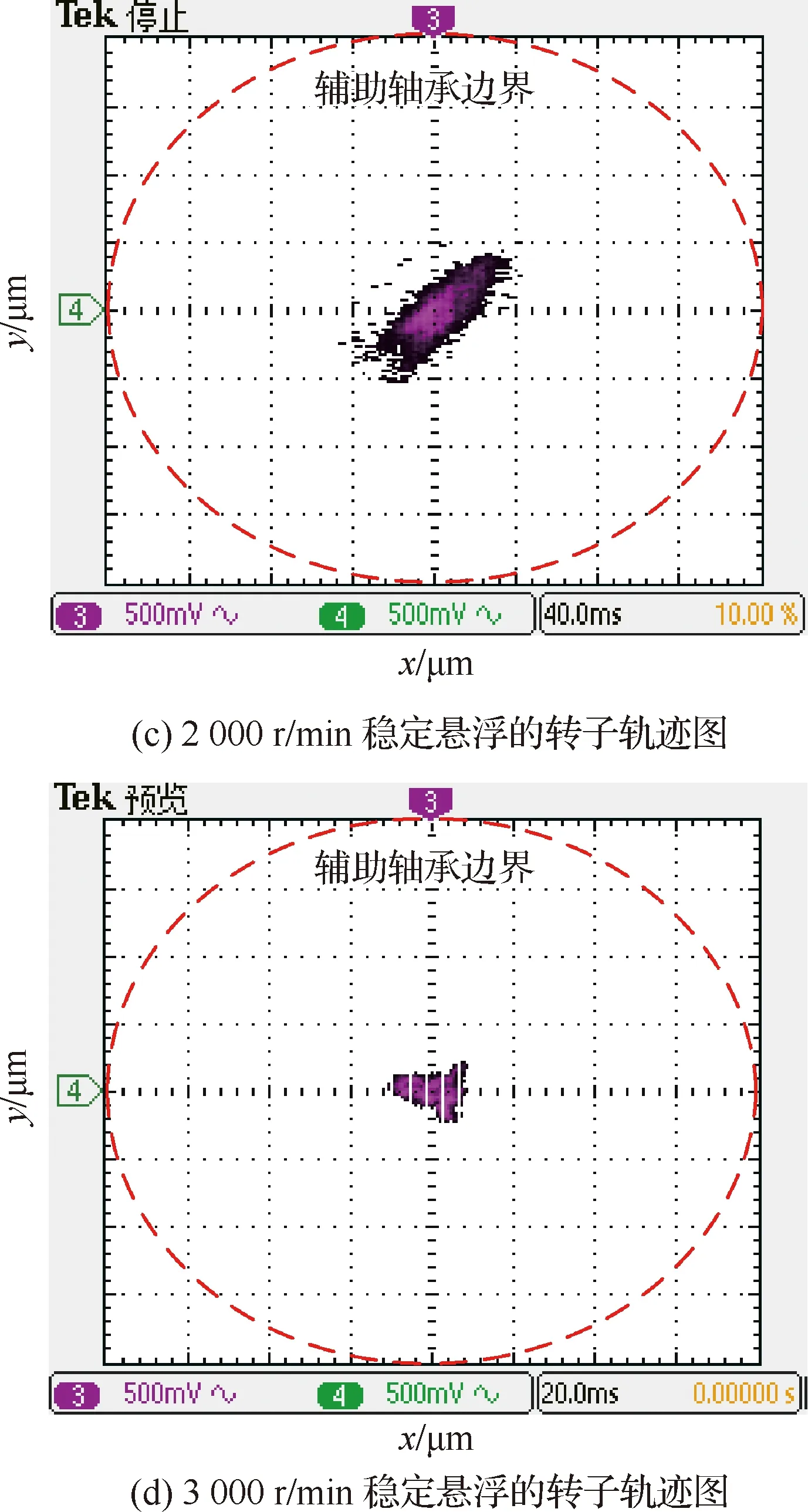
图15 不同转速下的悬浮位移实验波形Fig.15 Experimental waveforms of rotor displacement at different speeds
图16为电机转速在3 000 r/min稳定悬浮时绕组A1、B1、C1和A2、B2、C2的电流波形放大图,实验中通过测量电流调理电路的输出值观测电流大小,电流为0 A,对应示波器测得电压0.4 V,因此示波器通道零刻度线与电流零点之间的差值为0.4 V。绕组电流波形可验证电机按第2.1节提出的换相策略运行,且同一相的相对齿极绕组电流构成满足式(6)~式(9)设定,与图13(c)~图13(d)绕组电流仿真波形共同验证了电流控制的正确性。
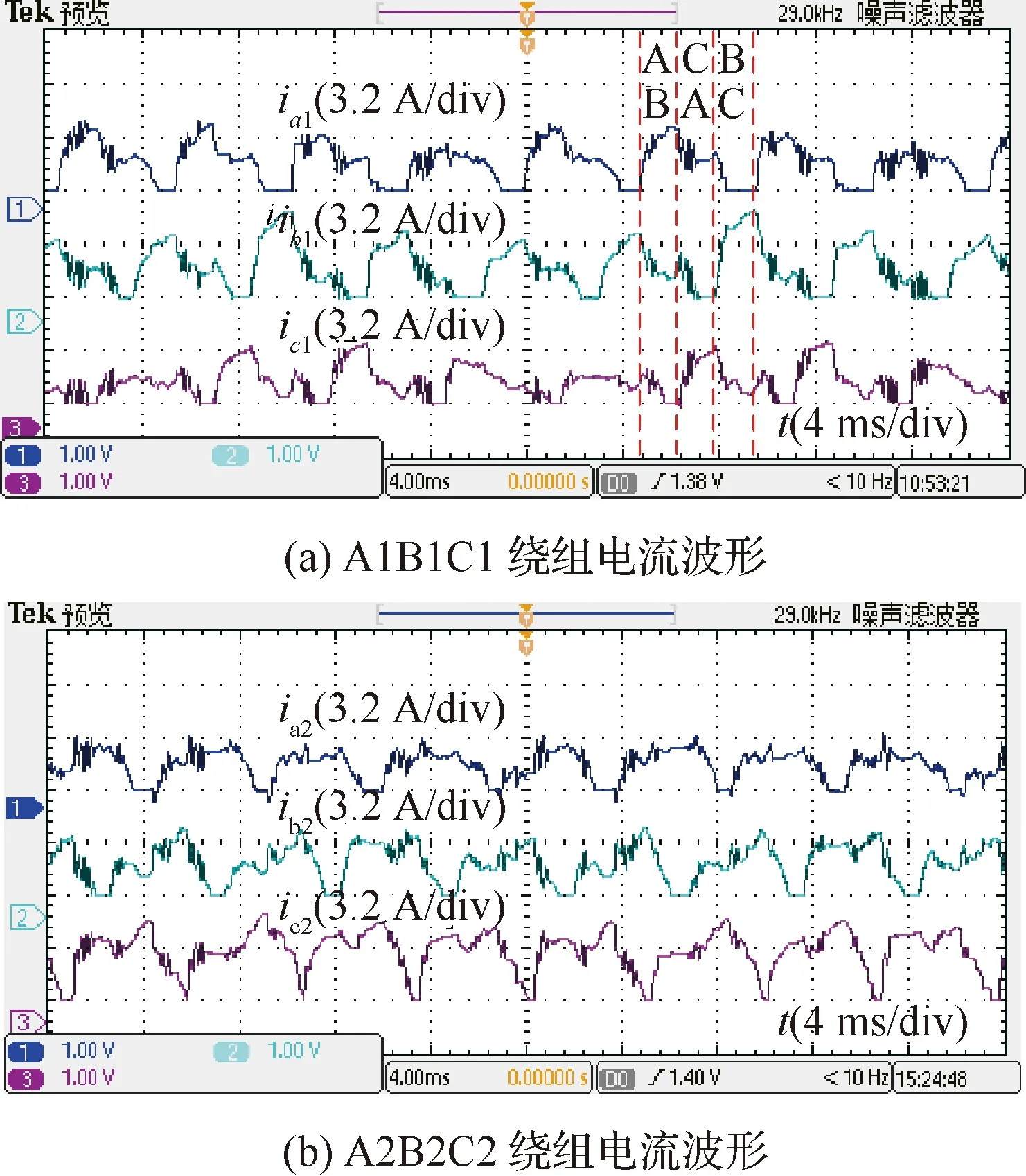
图16 3 000 r/min时的绕组电流实验波形Fig.16 Experimental waveforms of winding currents at 3 000 r/min
当转速在3 000 r/min时,在保持径向方向位移几乎不变的条件下,使用木槌沿径向方向敲击,进行径向负载突变实验,敲击前后方向径向位移及A相电流变化波形如图17所示,径向负载突变后转子位移偏差经过2.8 ms后迅速减小,证明所提方法具有较好的径向负载突变适应性。

图17 3 000 r/min时的径向敲击转轴实验波形Fig.17 Experimental waveforms of sudden knock on shaft at 3 000 r/min
在稳定悬浮状态下,转速闭环升、降速实验的位移、转速、转矩波形如图18所示。电机转速由3 000 r/min上升至3 500 r/min,调节时间约1.6 s;转速由3 500 r/min下降至3 000 r/min的调节时间约1 s。在转速调节过程中,转轴的径向位移波动较小,表明所提控制方法具有较好的动态悬浮性能。

图18 稳定悬浮时的升降速实验波形Fig.18 Experimental waveforms of speed changes with stable levitation
电机转速稳定在2 000 r/min时,进行A1绕组断路故障实验及A相2套绕组断路故障实验,电机转速、相电流波形如图19所示。图19(a)A1绕组断路后,由于转速闭环调节的作用,非故障齿极电流,如2、1均增大,以实现转速跟踪给定值2 000 r/min的目标。而图19(b)中当A相2套绕组均发生断路故障后,尽管非故障相电流增大以补偿A相缺失的转矩,但转速仍有约200 r/min 的跌落。表明故障发生后,6/4极BSRM依赖开关磁阻电机固有的强容错性能,仍具备一定的转矩输出能力。
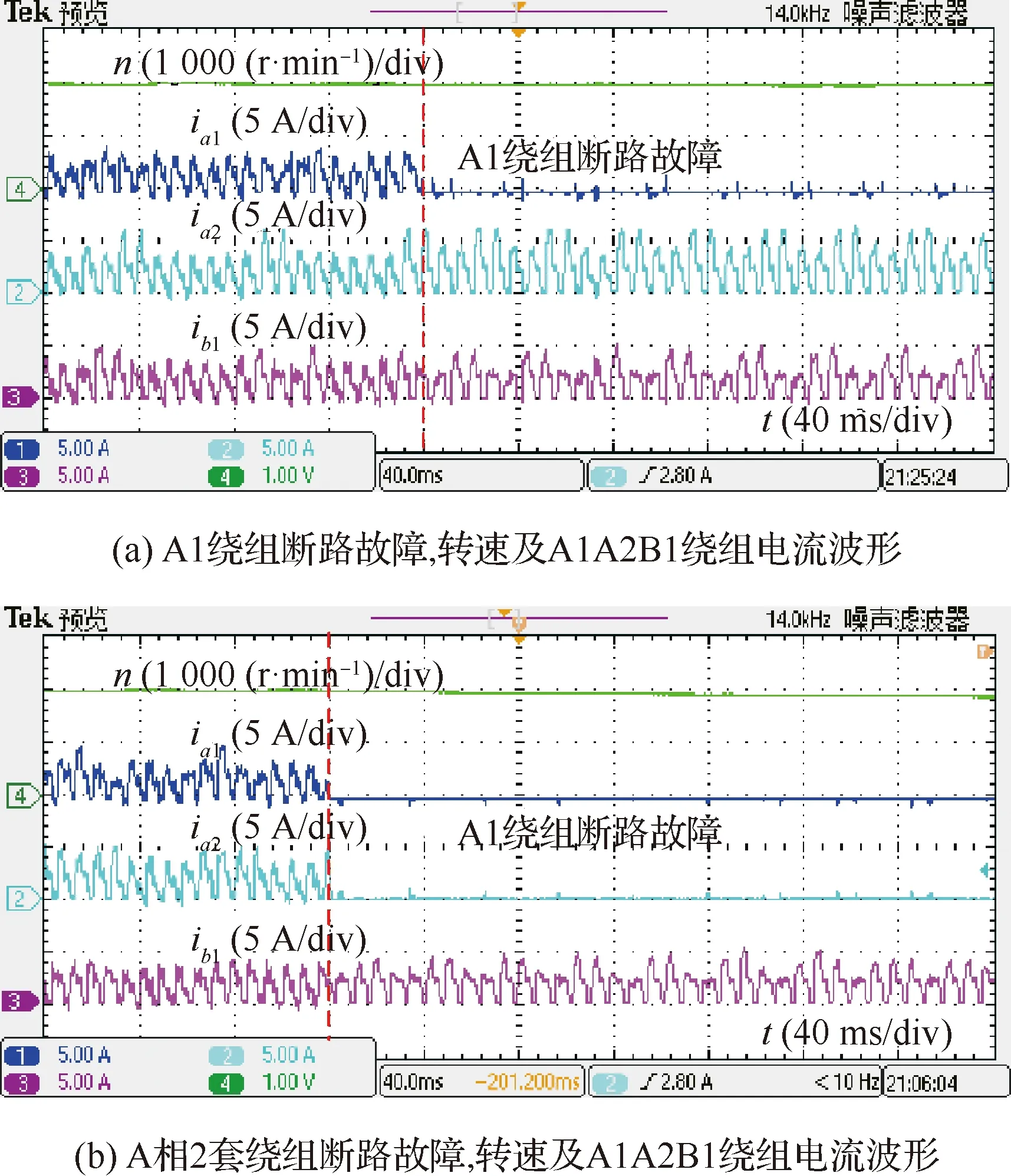
图19 2 000 r/min时的绕组断路故障实验波形Fig.19 Experimental waveforms of winding open circuit fault at 2 000 r/min
5 结 论
针对航空电机高集成度、高速化和高功率密度化的发展需求,本文研究了一种6/4极无轴承开关磁阻电机。针对该类电机悬浮原理的特殊性,提出转矩和径向悬浮力的协调控制方法。通过仿真和实验对该方法的正确性和可行性进行了验证,得到如下结论:
1) 与传统12/8极BSRM相比,6/4极BSRM具有结构简单的优势,绕组数目少,因而在降低换相频率的同时可减少主电路功率变换器桥臂数目,缩小系统体积。但为了实现转子稳定悬浮,6/4极BSRM采用双相导通模式,加剧了变量间的耦合程度,给控制带来一定的难度。
2) 所提控制方法减少了控制变量,简化了电机数学模型,合理分配了导通两相的悬浮力。
3) 应用本文提出的控制方法,6/4极BSRM在空载情况下实现了2 000 r/min和3 000 r/min的稳定悬浮,悬浮位移波动分别被控制在50 μm和25 μm以内,通过径向敲击实验和闭环升降速实验验证了该方法具有良好的负载突变适应性能和动态性能。
